变风速条件下风力机轴承故障特征提取
2021-10-13谷晓娇刘天顺李时雨
谷晓娇,刘天顺,李时雨
(沈阳理工大学,辽宁 沈阳 110159)
0 引言
轴承是风力机机械传动系统的核心部件,它的振动信号包含了丰富的状态信息,通过对其进行振动分析就可以实现轴承的故障诊断[1-2]。由于风力发电机组的工作环境具有噪声强、风速变化大的特点,会影响故障诊断的准确性[3-5]。
在强噪声环境下,常用的故障诊断方法是随机共振。随机共振(stochastic resonance,SR)的影响与系统参数有关,为了使随机共振法在工程应用中发挥出更好的效果,常将随机应变法与优化方法相结合。文献[6]采用频移尺度预处理和鱼群算法对随机共振系统参数进行同步优化,实现了齿轮故障微弱信号的提取。文献[7]将随机共振与经验模态分解相结合,基于遗传算法优化随机共振系统参数,实现了信号的自适应处理。文献[8]提出灰狼优化算法(grey wolf optimizer,GWO),由于其具有较强的收敛性能、参数少以及易实现等优点,因此,在工程优化领域的应用非常广泛。
风力机轴承的故障诊断在变风速条件下相当复杂。故障特征频率值随风速变化而变化。每次风速变化,系统参数都需重新优化。当风速变化时,利用变尺度系数R对频率-时间尺度进行变换,便可以处理不同风速条件下的振动信号。
综上所述,本文提出了一种基于灰狼优化算法和双稳态杜芬振荡器(bistable Duffing oscillator)的随机共振的故障特征提取方法,应用到风力机轴承的故障诊断中,并用实例验证了方法的有效性。
1 理论分析
1.1 随机共振理论
考虑到单位布朗颗粒在势场中的运动,其运动方程为
(1)
k为阻尼比;U(x)为势函数。
(2)

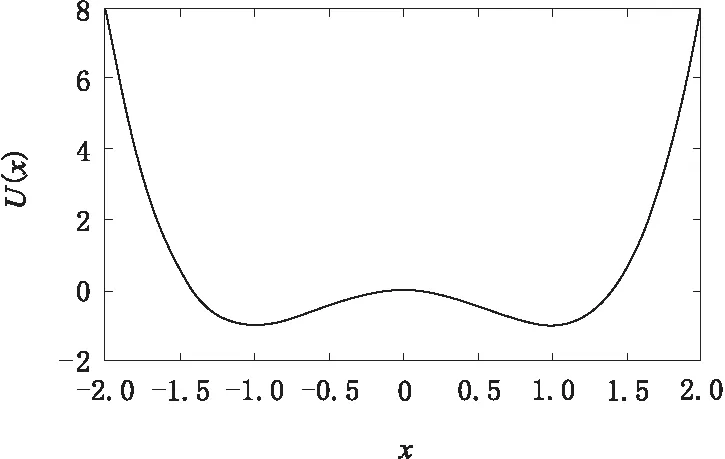
图1 势函数U(x)
1.2 灰狼优化算法
灰狼优化算法的优化原理源自于灰狼群体的等级机制和狩猎方式,灰狼处于生物圈食物链的顶端,通常群居生活。狼群中有严格的社会等级制度。在灰狼种群中按等级从高到低可分为α、β、δ和ω共4个层次的搜索个体,如图2所示。整个搜索过程主要由搜索个体集ω来实现。另外3个高级搜索人员共同负责指定ω移动的方向,然后ω将信息返回给3个高级搜索个体。α、β和δ通过反馈信息决定是否更新它们的位置。当迭代次数满足时,α的位置为最优解,β的位置为次优解,δ的位置为第3最优解[10]。
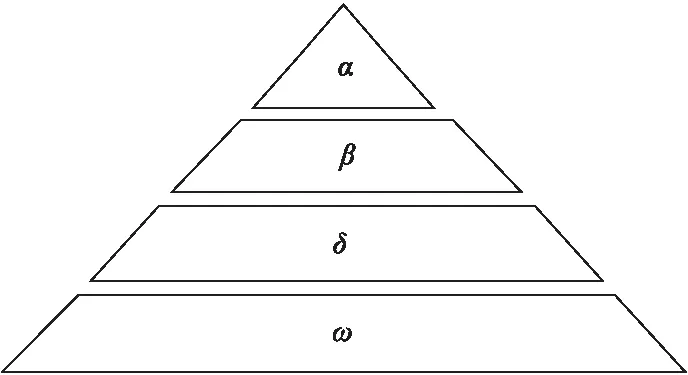
图2 灰狼社会等级
以d空间的位置为例,即环绕在第i阶段的目标位置为
(3)

(4)

(5)
(6)
r1和r2为[0,1]内的随机数。随着t的增加,参数a的值从2到0的线性减少。
(7)

(8)
(9)
(10)

2 方案设计
SR的性能主要体现在输出信号的信噪比[11]。因此,GWO的适应度函数为
(11)
PS为信号的有效功率;PN是噪声的有效功率。
风力机工作时,旋转部件的转速随风速变化而变化,这将改变零件的旋转频率,影响故障特征频率。而k、a、b的1组优化参数只能应用于1组输入信号,这表明每次风速变化,参数都需重新优化,这使故障特征提取过程复杂化。在引入可变尺度因子R进行频率-时间尺度转换后,可将1组优化参数应用于各种风速。
变尺度SR是一个等价的线性映射变换,它不会改变杜芬系统的输入信号特性。式(1)中,输入信号经过尺度变换后的频率为f′0=f0/R,对应的时间尺度更改为t′=Rt,尺度变换后的采样频率为fsr=fs/R。将相应的数值计算步骤改为h=R/fs,因此,式(1)可以表示为
(12)
式(12)为杜芬振荡器的变尺度SR方程,通过频时尺度变换实现不同频率信号的SR。将式(12)用变尺度因子R进行约简后恢复到时间尺度t,其等效方程为
Acos(2πf0t)+n(t)
(13)
通过比较式(12)和式(13),可以看出,式(12)为t′时间尺度上的变尺度SR方程,式(13)为t时间尺度上的变尺度SR方程,2个方程的响应相同,但频时尺度差为R倍。


图3 风力发电机轴承故障特征提取流程
3 实例验证
本实例轴承参数如表1所示,采用声学分析仪(B&K2250D)来采集加速度计的振动信号,采样频率fs=2 000.00 Hz,采样长度N=7 000。当风速为8.0 m/s时,采集风力发电机输入端高速轴承的振动信号,得到轴承旋转频率为20.00 Hz。其内圈故障轴承振动信号的时域信息和频域信息如图4所示。轴承的内圈故障特征频率为

图4 内圈故障轴承的振动信号的时频信息

表1 轴承的类型和参数
(14)
z为滚动体的数量;D为滚道节径;d为滚动体的直径;β为轴承的接触角;f0为轴承的旋转频率。当风速为8.0 m/s时,内圈故障轴承的故障特征频率为85.00 Hz。
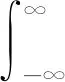

图5 风速8.0 m/s时的时域信息和频域信息

图6 风速11.5 m/s时的时域信息和频域信息
4 结束语
通过基于灰狼优化算法和双稳态杜芬振荡器的随机共振的故障特征提取方法,对风力机轴承的进行故障诊断,得出以下结论:
a.轴承故障特征的提取可以通过SR的杜芬系统来实现,系统参数和阻尼比都会影响随机共振的效果,与GWO方法的结合能够改善杜芬系统的性能。
b.风速的变化会影响轴承的故障特征频率,因此当风速变化时,需重新优化系统参数和阻尼比。可变比例因子R的引入,使得杜芬系统能够适用于不同风速下轴承的故障特征提取。
c.风力机轴承故障特征提取实验表明,GWO方法和随机共振相结合可以实现轴承故障特征提取。当风速发生变化时,通过可变比例因子R使原始优化结果也能用于故障特征的提取。
