匀质悬链几何形状的力学研究

李玉良 黄湘茹

（闽江学院物理学与电子信息工程系，福建 福州 350108）

1 引言

绳索、铁链、柔性电线等两端固定，悬挂空中在自重或其他外力作用下使用时通常被称为悬链，自重作用下悬链几何形状用“悬链线”描述.悬链是一类在工程力学和生产实际中有着广泛应用的工具，它可用于电力线路、水利吊装、桥梁施工、旅游或矿山索道、悬索桥、林业集运材索道、客运货运架空索道甚至纳米技术中，因而被广泛讨论［1～3］.早在1690年由雅各布.伯努利提出，伽利略等人曾猜想这条曲线是抛物线，但后来发现不对，最后由约翰·伯努利解出来，莱布尼茨把它定名为悬链线.生活中柔绳常用来晒衣服，当它空置时，有确定形状；当它放上被单时，形状改变；当它仅挂着若干衣架时，又是另外形状.大量经验告诉我们，当悬链上受到的外力的大小、方向、作用点分布之一改变时，悬链几何形状也随之改变，故探索悬链几何形状与所受外力分布关系不仅有趣而且有意义.

本文从力学原理出发，对悬链问题力学建模并求解；引出并探讨悬链几何形状与其受到外力分布之间的关联；最后对悬链线回禀的几何参量和力学参量间的关系、计算公式给出了严格推导.

2 外力作用下均质悬链的几何形状

2.1 自重作用下均质悬链的形状

设链的质量分布均匀且不随形状变化而改变，两端固定在A、B 两点，则悬链各微元的自重随各处链元的弧长正比分布，记它的线密度为λ、链长为S.如图建立坐标系，两端点的坐标为A（a1，b1）、B（a2，b2），最低点坐标为（x0，y0）.

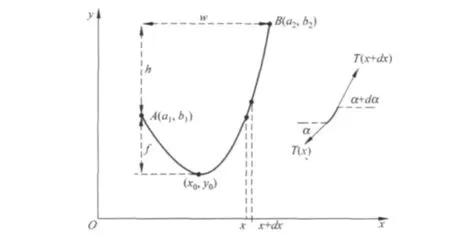
图1 均质悬链两端固定时仼一链元x→x＋dx 受力分析

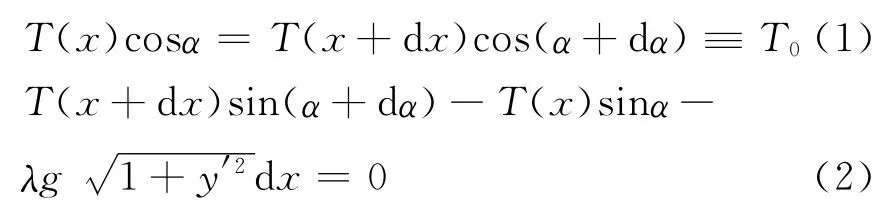
进而

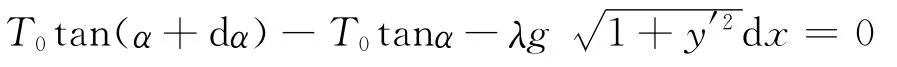
即

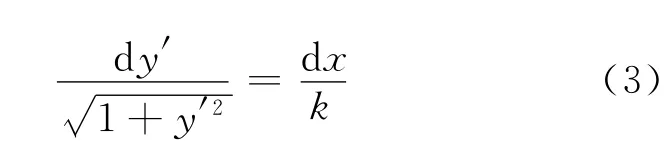
这里，T0、λ为均质链中间应力的水平分量和线质量密度且均是与位置无关的常量；k＝T0/λg，为悬链内禀的力学参量.此方式的通解为

设悬链 最 低点 坐 标为 （x0，y0），则 有 初 始条 件y（x0）＝y0，y′（x0）＝0，特解为

故悬链因自重而形成的几何形状为双曲函数曲线（通常被称为悬链线），x＝x0是其对称轴.显然，它不是圆弧线也不是抛物线，但当|x－x0|≪k时，由于

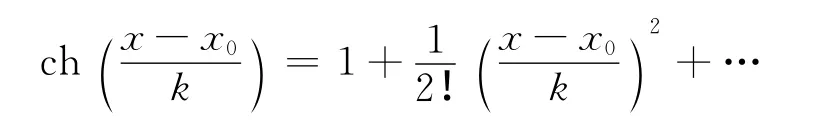
由（5）推出悬链线函数在x＝x0附近的泰勒展开为［4］

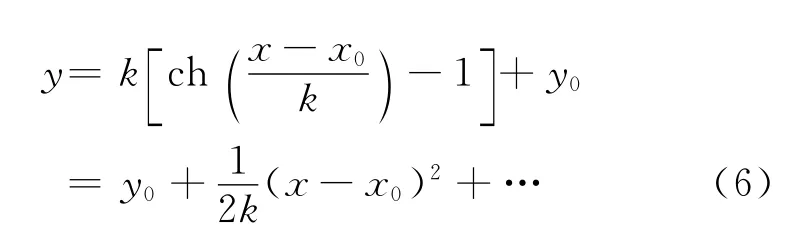
这个结果说明抛物线是悬链线的一级近似，条件|x－x0|≪k越满足近似越准确.

2.2 水平均匀荷载悬链的形状

悬索桥中的悬链，所承受的外力主要不是自重而是桥梁的重力，它在悬链的水平投影线上均匀施加.故假设悬链上任何一段质元受到的外力，其方向竖直向下、大小沿水平方向均匀分布，即与这一段在水平轴的投影长度成正比（比例系数标记为gλ0，λ0为常量、线质量密度量纲）.这种情况下，任意一段质元受竖直方向的外力dF＝gλ0dx，水平方向仍满足（1）式但竖直方向方程改变为

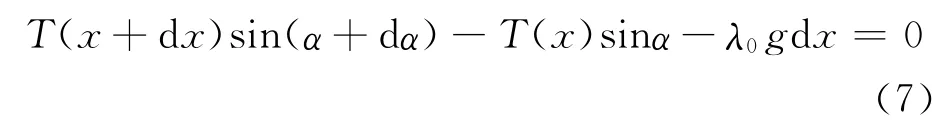
这里，k0＝T0/λ0g，方程化简后为k0y″－1＝0，特解为

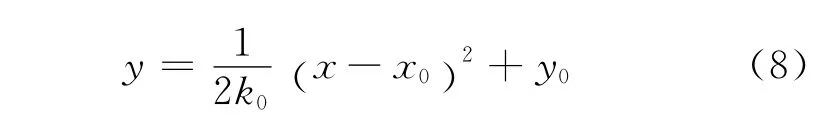
此时的悬链形状为抛物线.

2.3 悬链的几何形状与外力分布关系

由式（5）和式（8）推断：悬链的形状与它不同位置质元在竖直方向受到外力大小的分布密切相关.若这个关系是所受外力与链长成正比，则悬链形状为双曲线（即悬链线）；若这个关系是所受外力与悬链水平方向投影长度成正比，则悬链形状为抛物线（非悬链线）.悬空高压电线竖直方向受到的外力为电线自重，满足前者条件因而电线形状是悬链线；若悬线竖直方向受力主要不是自重而是负载，如悬链工路桥、用于挂窗帘布的轻绳，近似满足后者条件因而形状接近抛物线.

一般考虑，设作用在均质链上外力的线密度分布函数为dF＝gλ（x，y，y′）dx，则类似2.1节中分析，悬链形状曲线为方程

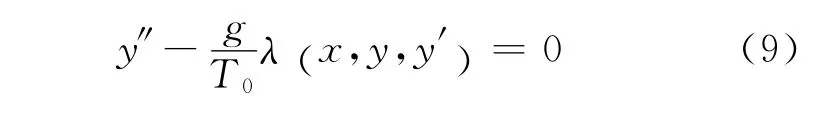
3 悬链线内禀参数关系

3.1 匀质链一般情形

选取悬链形状由悬链线描写.如图1所示，定义下列几何参数：两端点A、B 的水平方向和竖直方向的长度w、h，悬链下垂深度f

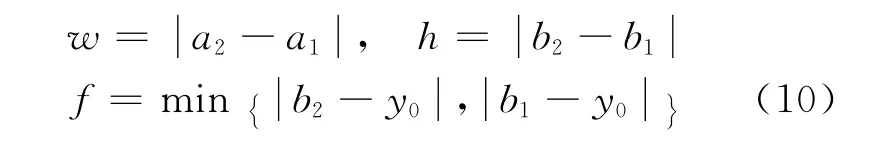
由于两端点A、B 在悬链线上，所以h和悬链弧长S 为

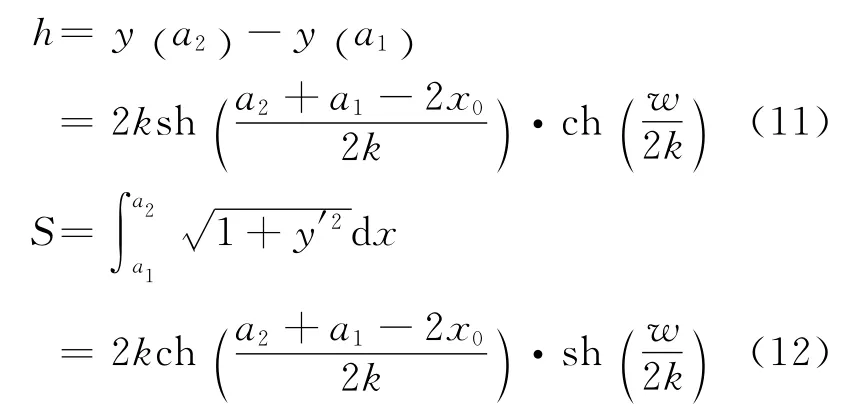
由此得由悬链内禀参数满足的关系式

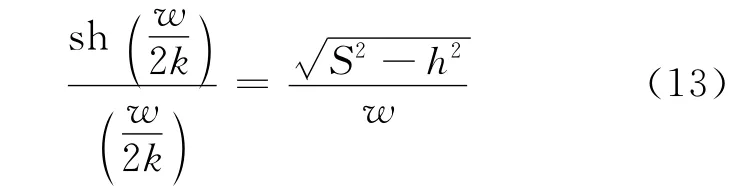
上式中含有悬链线几何参数w、h、S（由链长和端点位置决定）和力学参量k（k＝T0/gλ），四者相互制约.当均质链长度（S ） 一定，两端悬挂于固定点（即w、h 给定）时，则（1）力学参数k 确定；（2）悬链中各质元间内的水平应力T0与链的线质量密度λ成正比；（3）处于x 处质元间内应力

与T0一样与λ成正比.由（14）式，T （x） 仍然关于x＝x0对称，最低点（x0，y0）链元间的内应力最小（即为T0），离最低点越远链元之间的内应力越大.据此，可以定性解释制作手工拉面时常常发生的现象：被手抓住两端提起的条形面团，手握处快速变细，这样变化随面团向下惭惭变小，一段时间后变化停止面团形态稳定；因为手握处的面团内应力开始时最大，随着面团变细（λ↓）引起k↑（k＝T0/gλ），反过来导制内应力变小（参见式（14）），当各处粗细渐变的面团间内应力一致时面团变化停止.

3.2 端点在同一水平面上的悬链线

悬链下垂深度

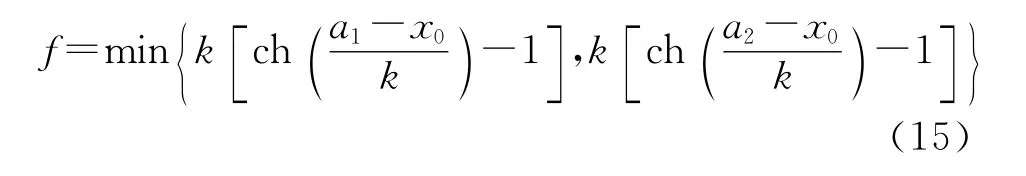
考虑悬链线两端点在同一水平面上，下垂深度f、参量关系（13）式变为［4］

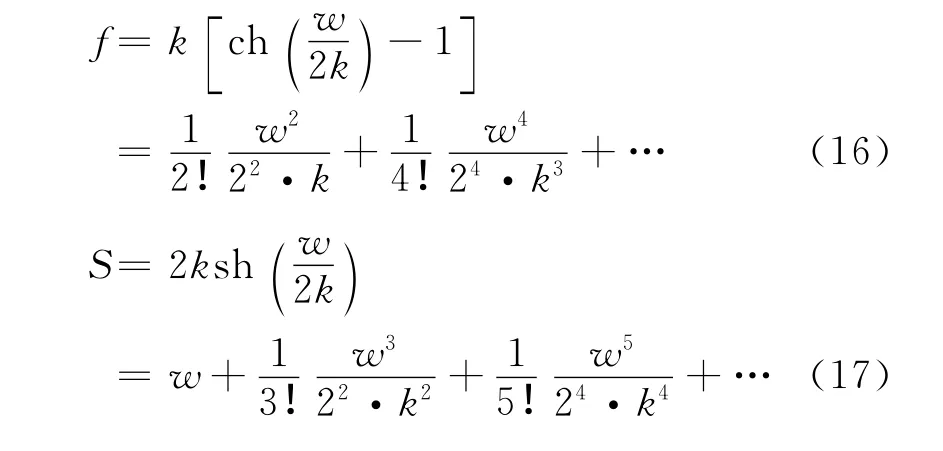
上式消去双曲函数得

从而

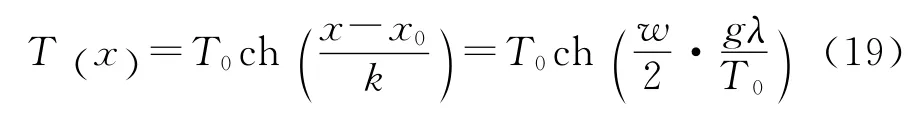
由上述四个公式可得出下列关于端点水平的悬链线的几个结论：（1）三个几何参量（w 、S、f）中只有两个独立；（2）端口的宽度（w ）、链长度（S） 确定，力学 参 量（k、T0、T （x） ）和 下 垂 深度（f） 随之确定，且与链的材质（λ） 无关（λ 变化被T0变化抵消）；（3）对于给定的均质链（S、λ 确定），只要给定端口宽度（w ），其他参量f、k、T0与T （x） 随之确定.

通常f≪S，S 与w 同数量级，由式（16）～式（18）可推出近似公式

在精度不严格情况下，式（20）中公式可方便计算.

4 小结

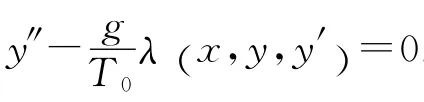
［1］郭致星，鲁束.悬链线模型和抛物线模型的差异性及其对ADSS设计影响［J］.电力系统通信，2003，（11）：35～37

［2］J.G.Bankstain，黄迅成.A note on catenary.扬州职业大学学报，2009，13（1）：1～5

［3］刑富冲.悬链线驰埀度的计算方法［J］.数学的实践和认识，2004，34（11）：98～101

［4］《数学手册》编写组.数学手册［M］.北京：高等教育出版社，1979.57～61