机器人辅助腹腔镜手术中的视觉测量方法研究

汪 祥，陈 柏，鞠 锋

(南京航空航天大学机电学院，江苏 南京 210016)

0 引言

在腹腔镜手术中，医生在患者腹部切开小口，在每个切口点经套管插入各种外科器械和内窥镜。监视器实时显示内窥镜拍摄的图像，医生依据监视器提供的视觉信息，操控手术器械以执行手术任务。在此过程中，内窥镜通常只提供二维图像信息，无法提供手术器械三维空间中的位姿信息。而在机器人辅助腹腔镜手术中，快速而准确地获取手术器械三维位姿信息是机器人手术走向智能化的前提[1]。

目前，在国外，Krupa等[2-3]以激光光斑和LED灯作为标记，解决了在人体器官附近控制手术器械动作的问题；Speidel等[4]提出了一种基于不同的视觉特征来分割手术器械尖端的方法，并在跟踪手术器械的过程中使用了多对象粒子滤波；Haase等[5]使用3-D ToF/RGB内窥镜跟踪手术器械，实验中工具尖端的定位误差在4 mm以内；Khoiy等[6]研制了一种持镜机器人的自主控制系统，能够通过处理术中实时影像实现自动追踪无标记的手术器械；Shin等[7]研究了一种使用单个相机配合标记物的手术器械追踪技术，此技术可以获取腹腔镜手术器械位置、抓取角度和横滚角度，用于腹腔镜手术模拟。

在国内，潘晗倩[8]研究了在X射线图像中动态追踪穿刺针并绘制其延长线的方法，采用了霍夫直线检测算法来检测穿刺针的直线特征并据此动态更新图像中的参考线；刘大鹏等[9]设计了一套基于单目视觉和设置固定标识的手术导航系统；胡天策等[10]利用透视投影成像的几何关系以及内窥镜在术中移动的位移差，提出一种基于内窥镜单目视觉测量距离和病灶大小的方法;赵子健[11]提出了一种腹腔镜手术器械三维实时跟踪方法，该方法以手术器械插入点和环形标记的位置测量为基础，并与器械的深度估计相结合;于凌涛等[12-13]建立了一种基于3D动态视觉窗口引导的器械臂运动算法。

本研究参考了已有的手术器械位姿测量方法，针对腹腔镜手术器械位姿测量，提出了一种快速的位姿测量算法并设计了手术器械位姿测量方案。

1 共线PnP问题的一般解法

本文采用常见的单目内窥镜和中心透视投影相机为研究对象。针对在腹腔镜手术场景下视觉测量手术器械位姿，解PnP问题是一个可行的方法，即“给定n个控制点的空间相对位置并给定由射影中心点到n个控制点的角度，求取射影中心点到各个控制点的距离”[14]。共线PnP问题如图1所示。

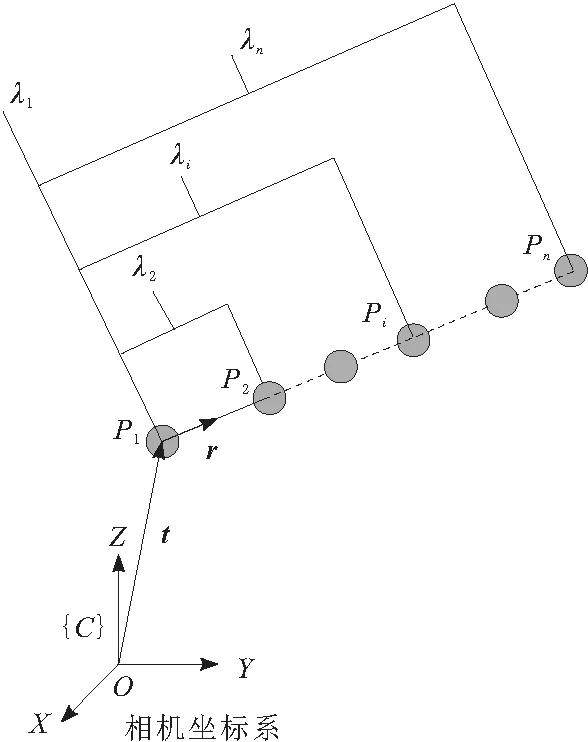
图1 共线PnP问题

空间中点P1,P2,…,Pi,…,Pn在同一直线上，已知任一点Pi与编号起点P1的距离为λi，其图像坐标为(ui，vi)，相机的内参数矩阵为K。设编号起始点在相机坐标系下的位置向量为t，直线的单位方向向量为r，根据相机内参数模型可以得到：

(1)

式(1)可以改写为

(2)

式(2)可以转换为经典的优化问题：

min‖Arr+Att‖,rTr=1

(3)

当n≥3时，式(3)有解，其解是由对称矩阵E的奇异值分解得到的。

(4)

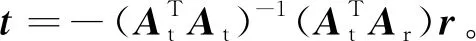
Ar和At定义为

2 手术器械位姿测量方案

应用以上算法测量手术器械的位姿需要相机内参数、标记的几何参数和标记点在图像上的投影。在得到标记点的空间位置之后，仍需要根据标记点和手术器械之间的几何关系得到手术器械的三维表达。所以本方案由相机标定及畸变校正、标记设计、图像处理、标记点三维位置计算和手术器械的三维表达5个部分组成。

2.1 相机标定及畸变校正

相机标定就是利用世界坐标系中的已知三维点坐标和它在图像中的像点坐标之间的投影关系,计算相机的内外参数的过程。本研究采用常用的Bouguet工具箱进行相机的标定工作，标定过程见文献[15]。

相机标定结果如表1所示。其中,fx，fy是以像素为单位的焦距；(u0,v0)是主点坐标。

表1 相机内参数标定结果

由表1的数据可以得到相机的内参数矩阵为

(5)

相机的畸变系数如表2所示。在此次标定中设置了k5不标定，即默认k5=0。

表2 相机畸变系数标定结果

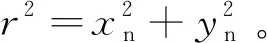
(6)

(7)

相机畸变校正过程中，真实图像I和畸变图像Id之间的关系为I(u,v)=Id(ud,vd)。首先根据式(8)可以得到真实图像像素(u,v)对应的归一化坐标(xn,yn)，再根据式(7)可以得到畸变后的归一化坐标(xd,yd)，根据式(9)得到对应的畸变图像像素(ud,vd)。此时得到的ud和vd可能并非整数，需要经过插值处理才能得到像素值Id(ud,vd)，最后赋值给I(u,v)。循环以上过程，找遍真实图像中所有的像素点，即可获得真实图像。

(8)

(9)

2.2 标记设计

为方便在内窥镜图像中检测标记，设置标记颜色为人体中不常见的绿色，测得圆环直径d=5 mm，λ1=0,λ2=10 mm,λ3=20 mm ，将标记贴于手术器械上，如图2所示。

图2 带有标记的手术器械

2.3 图像处理

体外仿真环境下相机拍摄并校正畸变的一副图像I。将图像的色彩通道分离：R=I(:,:,1)、G=I(:,:,2)和B=I(:,:,3)。根据式(10)得到二值图像W，其中，T1、T2是可以调节的阈值，可以根据具体的状态进行调节，影响T1、T2的因素主要是光照和绿色标记所用的颜料。处理图3中的图像时，取T1=20、T2=20。

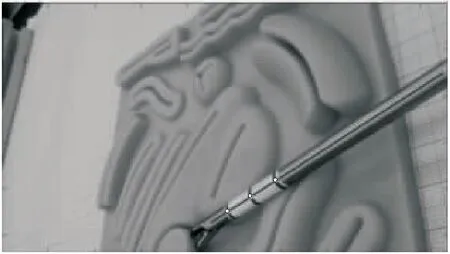
图3 内窥镜在体外实验中拍摄的图像

(10)

处理二值图像W的目的是获取标记区域的形心。首先分割出二值图像中的八连通区域，再计算各个连通区域的面积，筛选出其中面积最大的3个区域即为3个绿色标记的图像区域，对区域中的图像坐标求平均，得到各自连通区域的形心。用最小二乘法将3个形心拟合成1条直线，该直线可视为手术器械直杆影像的中心线，如图3所示。图3中白色点为标记区域的形心，经过白色点的直线为直杆影像的中心线。

2.4 标记点三维坐标计算

在前文所述算法中，输入所得到的3个标记区域的形心坐标，相机内参数矩阵K，以及λ1、λ2、λ3，可以输出标记点所在直线的位置向量t和对应的单位方向向量r。进而求得P1、P2和P3在相机坐标系下的位置向量为CP1、CP2、CP3。

2.5 手术器械的三维表达

本研究使用手术器械直杆中心线的方程h=M+ql来表达手术器械的位姿。其中，h是直杆中心线上任意一点的位置向量；M是直杆中心线上某固定点的位置向量；l是直杆中心线的单位方向向量；q是位置向量为M的点沿着l方向与位置向量为h的点的距离。

手术器械与不同坐标系的示意图如图4所示。

图4 手术器械位姿视觉测量

(11)

(12)

(13)

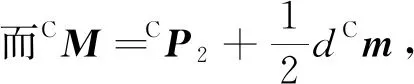
(14)

在算得Cl和CM之后，根据式(11)和式(12)可以求得Bl和BM。

对于手术器械直杆中心线上任意一点，几何测量得到其沿着l方向与M点的距离q0，即可求得其在相机坐标系下的位置向量Ch0=CM+q0Cl,以及其在机器人基座坐标系下的位置向量Bh0=BM+q0Bl。

3 精度实验

3.1 实验方案

本实验旨在体外模拟环境下对上述手术器械位置测量方法的可行性以及测量精度进行测试。

实验装置由PC(个人电脑)、UR5机器人、直杆腹腔镜和腹腔镜模拟训练模块等组成，如图5所示。直杆腹腔镜的分辨率为1 920×1 080。PC通过USB和直杆镜头相连，通过网线和UR5机器人相连。PC上运行MATLAB作为主控制器，通过Image Acquisition Toolbox获取直杆镜头拍摄到的图像，通过和UR5机器人的Socket通信,获取UR5机器人末端法兰坐标系相对于基坐标系的位置和姿态。

图5 腹腔镜手术机器人持镜臂实验平台

精度是多次重复测量某一量时，各测定值之间相一致的程度，表征测量的随机误差大小。为度量上述测量方案的精度，在保持手术夹钳和机器人基坐标系相对静止的情况下，从不同的角度拍摄手术器械的图像，并根据第2节所述方案计算Bl和BM。本研究根据式(15)计算M点位置测量的平均偏差，式中Xi为BM的各次测量结果。Bl在X、Y、Z3个方向的分量为lx、ly、lz。式(16)中的xi分别代入lx、ly、lz的各次测量结果，得到lx、ly、lz测量结果的标准差σx、σy、σz。式(15)和式(16)中,n是测量的总次数，i=1,2,…,n。

(15)

(16)

3.2 实验结果

实验中，从不同的角度分别拍摄了14幅图像，即n=14，分别基于各个图像和相应的机器人的位姿,计算了M点在机器人基坐标系下的坐标BM和直杆中心线的方向向量在机器人基坐标系下的表示Bl。

14次测量得到M点在机器人基坐标系下的位置。计算每个M点测量位置与平均测量位置的距离如图6所示。14个偏差距离的最大值为16.3 mm，最小值为1.2 mm,平均偏差为5.5 mm，测量位置与平均测量位置的距离的标准差为3.8 mm。

图6 点M测量位置与平均测量位置的距离

直杆的单位方向向量Bl在机器人基坐标系下的3个分量分别为lx、ly、lz，如图7所示。lx的最大值为-0.12，最小值为-0.23，平均值为-0.18，标准差σx=0.027。ly的最大值为0.99，最小值为0.97，平均值为0.98，标准差σy=0.005。lz的最大值为0.03，最小值为-0.12，平均值为-0.05，标准差σz=0.043。

图7 Bl在X、Y、Z方向的分量大小

4 误差分析

鉴于测量的误差较大，猜测是相机参数和机器人手眼参数标定不够准确的原因。故而重新使用Bouguet工具箱对相机参数进行了标定，在标定过程中选取了25幅更为清晰的图像。得到了不确定度更小，并且考虑了相机畸变参数k5(即k5≠0)的相机参数。重新在30个持镜位姿下测量了手术器械的位置和方向，得到手术器械的位置和方向的测量结果如图8和图9所示，测量结果的密集程度更高。在图8中，测量点的平均偏差为1.3 mm,较于图6中的结果精度更高。在图9中，3个方向的分量的测量结果的标准差σx、σy、σz分别为0.003、0.001和0.011，较图7中的测量结果波动更小，测量精度更高。

图8 相机重新标定后点M测量位置与平均测量位置的距离

图9 相机重新标定后Bl在X、Y、Z 3个方向分量大小测量结果

由此可以看出测量精度的主要影响因素有相机内参数的标定精度以及相机畸变模型的准确性。进一步地，可以推测UR5机器人以及本文所介绍的视觉测量算法引起的误差并不占主导。

此外，由于本文所做实验都是在光照条件良好、背景干扰少的条件下进行的，在体内的环境中还要考虑光照不足、血污和雾气等恶劣条件引起的误差。

5 结束语

本文提出了一种基于求解共线PnP问题的手术器械位姿视觉测量方法，包括相机标定及畸变校正、标记设计、图像处理、标记点三维坐标计算和手术器械的三维表达，并对所提出的视觉测量方法进行了精度测试实验，实现了提取腹腔镜的二维图像信息并将其转换为手术器械在三维空间中的位姿信息。对测量的误差进行了分析，发现相机内参数的标定精度对测量精度影响较大。

测量结果表明，目前所提出的手术器械位姿检测方法的精度尚不满足指引机器人自主进行准确的手术操作如切除和缝合等的要求。但该方法仍然具有一定的应用价值。一方面测量精度可以被提高以达到应用要求，可以通过使用更高精度的相机、更准确的参数标定等方式提高测量的精度。另一方面，本研究在对手术器械的位姿精度要求不高的场合，如腹腔镜手术过程中的视觉追踪和手术器械的辅助定位等具有良好的应用前景。