基于混合学习果蝇优化算法的冗余机械臂逆运动学求解

2021-10-13石建平李培生刘国平

农业机械学报 2021年9期

石建平李培生刘国平朱林

(1.贵阳学院电子与通信工程学院，贵阳 550005; 2.南昌大学机电工程学院，南昌 330031)

0 引言

机械臂逆运动学问题描述了从末端执行器的笛卡尔空间到关节空间的映射关系，它是对机器人运动控制、轨迹规划以及作业空间分析等问题展开研究的前提与基础，该问题的求解方法有封闭解法和数值解法[1]。其中，封闭解法具有计算速度快、精度高以及能求出所有逆解等优点，但封闭解法受机械臂结构的限制较大，只适宜于求解关节结构模型简单且机构构型特定(即结构满足Pieper准则)的机械臂的逆运动学。对于机构不满足Pieper准则的冗余机械臂，其运动学逆解只能用数值解法来获得。常用的运动学逆解数值求解方法有Jacobian矩阵迭代法[2-3]、神经网络法[4-6]等。其中，Jacobian矩阵迭代法每一次迭代都需要进行求导运算以及Jacobian矩阵的求逆运算，求解过程复杂且存在奇异性问题，同时迭代初值的选择对逆解的求解质量与求解效率影响较大；神经网络法需要大量的样本数据来进行网络的训练学习，网络学习所需时间较长，不适宜实时控制，且大量训练样本在实际中较难获取。

近年来，遗传算法[7-8]、粒子群优化算法[9-12]、差分进化算法[13-14]、人工蜂群优化算法[15]、萤火虫群优化算法[16]、生物地理学优化算法[17]等智能优化算法被广泛应用于解决机器人的逆运动学问题并获得了良好的研究进展，但在求解结构复杂冗余机器人的逆运动学问题时，上述算法的收敛速度、收敛精度以及寻优结果的稳定性等各项寻优指标仍需进一步提高。

果蝇优化算法(Fruit fly optimization algorithm，FOA)是PAN[18]提出的一种群智能优化算法，该算法凭借其寻优机制简单、控制参数少、收敛速度快、易于理解及容易编程实现等优点而受到广大研究者的关注，并在多维背包问题[19]、神经网络训练[20]、电力负荷预测[21]、半导体测试调度[22]、种子园规划设计[23]、农产品检测[24]等诸多领域得到成功应用。然而，由于基本FOA算法中的气味浓度判定值不能取负值，导致该算法无法优化决策变量为负值的优化问题，且FOA算法只向种群最优个体学习的简单搜索方式导致该算法在解决复杂优化问题时容易“早熟”而陷入局部极值。本文以冗余机械臂运动学逆解的有效求解为目标，对基本FOA算法进行改进研究，提出基于混合学习果蝇优化算法(Hybrid learning fruit fly optimization algorithm，HLFOA)的冗余机械臂运动学逆解求解方案，用7自由度冗余机械臂的逆运动学求解验证所提出方法的可行性与有效性。

1 问题描述

以7自由度YuMi 14000 ABB型双臂工业机器人[6]的左臂为例来讨论逆运动学求解问题，机器人如图1所示，机器人左臂的D-H参数如表1所示。表中参数θj、αj、dj、aj、lj及uj(j=1, 2,…,7)分别为关节角变量、连杆扭转角、连杆偏距、连杆长度、连杆关节角变量的下限及上限。

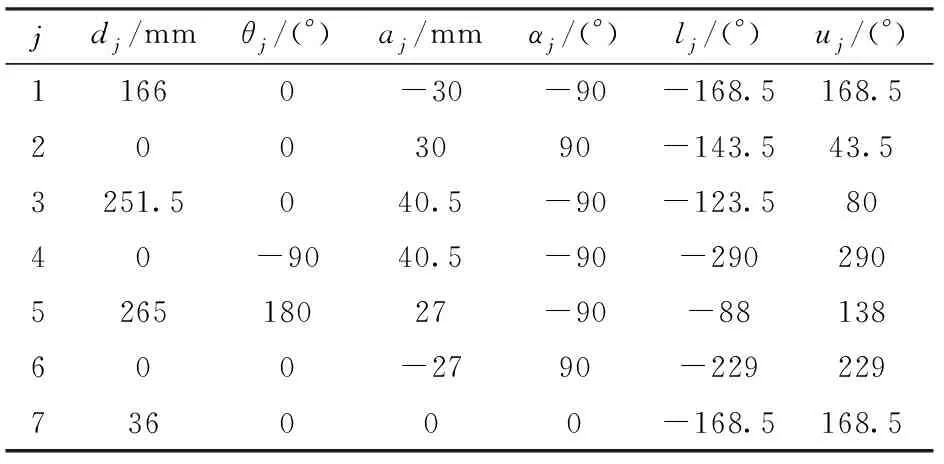
表1 YuMi 14000 ABB型工业机器人左臂D-H参数Tab.1 D-H parameters for left arm of YuMi 14000 ABB industrial robot

根据表1中的D-H参数，可得相邻坐标系的齐次变换矩阵为

(1)

式中cθj=cosθj、sθj=sinθj、cαj=cosαj、sαj=sinαj。

于是，可得该机械臂左臂的正向运动学方程为

(2)

式中R——机械臂末端执行器的姿态矩阵

P——机械臂末端执行器的位置向量

可见，7自由度冗余机械臂的正向运动学方程是以关节角变量θ1、θ2、…、θ7为自变量的复杂函数，这是一组多变量强耦合的非线性方程组，无法用常规的封闭解法获得机械臂的运动学解析逆解。

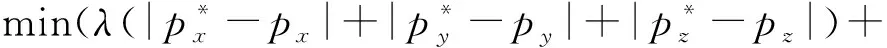
(3)

2 果蝇优化算法的改进

2.1 基本FOA

根据文献[19]，FOA算法的寻优步骤如下：

(1)随机初始化果蝇种群位置:X_b，Y_b。

(2)更新果蝇个体i的位置

(4)

式中RandomValue——固定区间内随机生成的步长

(3)果蝇i与坐标原点的距离Disti和果蝇个体i的气味浓度判定值Si的计算式为

(5)

(6)

(4)将气味浓度判定值Si代入气味浓度判定函数f(·)(即优化问题的适应度函数)，得到果蝇个体i的气味浓度为

Smelli=f(Si)

(7)

(5)找出种群中气味浓度最高的果蝇个体bestIndex(针对最小优化问题，适应度函数的取值越小，表明对应果蝇个体的气味浓度越高)

[bestSmellbestIndex]=min(Smelli)

(8)

(6)保存最高气味浓度及其对应的位置坐标，果蝇种群利用视觉飞向该位置

(9)

(7)重复循环步骤(2)～(5)，如果当前的最优气味浓度优于上一代的最优气味浓度，并且当前迭代次数小于最大迭代次数，则执行步骤(6)；否则，算法输出寻优结果并结束循环。

可见，FOA算法每次迭代都是在最优果蝇个体位置的固定范围内进行局部搜索，如果该位置属于局部最优，则算法将容易“早熟”而陷入局部极值。

2.2 改进的FOA

2.2.1候选解的线性产生机制

根据式(6)可知，FOA算法中的气味浓度判定值Si与距离Disti成反比，候选解采用了非线性的产生机制，同时气味浓度判定值Si不能取负值。因此，FOA算法无法优化含负值搜索空间的优化问题，且无法在指定区域内进行均匀搜索，使得算法的全局搜索能力不强。

由表1可知，冗余机械臂的关节角取值范围含负值空间，显然基本FOA算法无法解决本文的机械臂逆运动学问题。本文HLFOA算法中，果蝇个体i用位置向量Xi=(θi1,θi2,θi3,θi4,θi5,θi6,θi7)来表示(θi1,θi2,…,θi7分别表示冗余机械臂的7个关节角)，则Xi代表机械臂逆运动学问题的一个候选解。为克服基本FOA算法中候选解不能取负值以及候选解非线性产生机制的不足，本文采用智能优化算法常使用的线性候选解产生方案，即直接按Si=Xi得到果蝇的气味浓度判定值。于是，HLFOA算法在克服FOA非线性候选解产生机制缺陷的同时，通过舍弃果蝇位置距离的计算简化了算法的进化环节和降低了算法的计算成本。

2.2.2嗅觉搜索

由式(4)可知，FOA算法的嗅觉搜索总是在种群最优果蝇个体附近的固定范围内进行局部搜索，这种只向种群最优个体学习的搜索方式能够有效加速算法的收敛速度，同时也使得算法寻优的收敛质量主要依赖于种群的最优个体。如果种群的最优个体处于局部最优，则FOA算法容易“早熟”而陷入局部极值，致使FOA算法在解决复杂多模优化问题时全局搜索能力并不强。

受粒子群优化算法[25]的启发，HLFOA算法给果蝇个体赋予了记忆功能，即果蝇i能够记忆自身进化过程中最佳历史位置Pi，所有的Pi构成了最佳历史种群P；整个果蝇种群的历史最佳位置用Gb表示。为克服FOA算法只向种群最优个体学习所导致的不足，果蝇嗅觉搜索过程中应当同时兼顾学习的广度与深度，为此， HLFOA算法采用嗅觉搜索策略

(10)

(11)

式中ω——扰动比例因子与学习概率

r、r′——[0,1]内均匀分布的随机变量

t——当前迭代次数

tmax——算法的最大迭代次数

r1、r2、r3满足r1≠r2≠r3≠i。

2.2.3越界处理

为进一步确保搜索过程果蝇种群的多样性与随机性，对于下一代果蝇位置向量Xi(t+1)中超出位置边界的分量θij算式为

θij=lj+(uj-lj)k

(12)

式中k——[0,1]内均匀分布的随机变量

2.2.4视觉实时更新

视觉搜索是指对果蝇种群最优位置进行更新。在FOA算法中，当前代的所有果蝇个体完成嗅觉搜索后，如果当前种群的最优位置优于上一代果蝇种群的最优位置，则对种群的最优位置进行更新。为进一步提高算法的收敛速度，果蝇个体的最新成功搜索经验应该实时分享给其他未进化个体，因此HLFOA算法采用实时更新方案，即

(13)

(14)

可见，HLFOA算法中的视觉搜索本质是指对果蝇个体历史最优信息以及种群历史最优信息的实时更新，从而为其他果蝇个体的嗅觉搜索提供最新的成功搜索经验。

2.2.5算法计算成本

由于优化目标函数的评估次数是影响算法计算成本的主要因素，本文以优化目标函数的总评估次数来衡量算法的计算成本(设种群规模为m和最大迭代次数为tmax)。HLFOA算法在初始化阶段需要的优化目标函数评估次数为m，在循环迭代阶段优化目标函数评估次数为mtmax，因此，HLFOA算法总的优化目标函数评估次数为mtmax+m； FOA算法在初始化阶段需要的优化目标函数评估次数为1，在循环迭代阶段的优化目标函数评估次数为mtmax，因此，FOA算法总的优化目标函数评估次数为mtmax+1。

可见，HLFOA算法的改进策略并没有导致计算成本的显著增加。

2.2.6逆运动学求解步骤

基于HLFOA算法的冗余机械臂逆运动学求解步骤如下：

(1)设置果蝇种群规模m与算法的最大迭代次数tmax，在关节空间内对所有果蝇个体进行随机初始化，果蝇i的当前位置Xi即为其历史最佳位置Pi，种群中的最优位置即为种群的最佳历史位置Gb，设置i=1、t=1。

(2)按式(10)、(11)对果蝇i执行嗅觉搜索，按式(12)对得到的下一代果蝇位置向量进行越界处理。

(3)根据式(3)对下一代果蝇i的位置向量进行实时评估，按式(13)、(14)分别更新果蝇i的历史最佳信息及种群的历史最佳信息。

(4)如果i

(5)如果t

3 试验结果与分析

3.1 给定期望位姿的运动学逆解

为检验HLFOA算法解决冗余机械臂逆运动学问题的有效性，将HLFOA算法的优化求解结果与算法FOA、LGMS-FOA[26]、AE-LGMS-FOA[27]、IFOA[28]及SFOA[29]的求解结果进行对比分析。所有算法的种群规模为100，最大迭代次数为1 000；由表1可知，机械臂末端执行器的位置分量可达102mm数量级，而其姿态分量的绝对值都满足小于等于1，为能够有效平衡算法求解过程中的位置误差与姿态误差，将误差调整因子设置为λ=10-2；算法FOA、LGMS-FOA、AE-LGMS-FOA、IFOA及SFOA的相关参数按对应文献的推荐值进行设置。算法采用Matlab R2013a编程实现，程序运行环境为：Intel Core(TM)i7-7700、3.6 GHz、16 GB内存、Windows 10操作系统。

给定YuMi 14000 ABB型双臂工业机器人左臂末端执行器的期望位姿矩阵为

各算法分别独立连续优化求解10次的最优适应值、平均适应值、最差适应值以及适应值标准差如表2所示。各算法求得的1组最优逆解所对应的位姿误差如表3所示，各算法的平均适应值收敛曲线如图2所示。

表2 不同算法逆解寻优结果统计(给定期望位姿)Tab.2 Performance statistics of different algorithms (given desired pose)

表3 不同算法的位姿误差Tab.3 Pose errors of different algorithms

由表2可知，HLFOA算法逆解运算寻优适应值的平均值、最优值、最差值以及标准差都优于其余算法，其寻优平均适应值、适应值的标准差分别可达10-16和10-17数量级，说明HLFOA算法具有逆解寻优精度高且寻优结果稳定性好的优点。从表3可知，HLFOA算法最优逆解对应的位姿误差最大分量为10-16数量级， LGMS-FOA和AE-LGMS-FOA最优逆解对应的位置误差最大分量分别为101、100数量级，FOA、IFOA及SFOA算法最优逆解对应的位置误差最大分量则高达102，说明HLFOA算法的最优逆解能够使得机械臂末端执行器以很高的精度收敛于期望位姿，而其余算法的最优逆解存在较大的位姿误差。

由图2可知，HLFOA算法的平均适应值收敛曲线具有最快的下降速度并获得了最低的下降位置，同样说明了HLFOA算法获得了比其他算法更快的收敛速度和更高的收敛精度。

3.2 任意期望位姿的运动学逆解

为进一步检验算法求解运动学逆解的泛化能力，针对YuMi 14000 ABB型双臂工业机器人左臂末端执行器位姿空间的10个任意的期望位姿矩阵，用上述各算法进行寻优求解的适应值如表4所示(算法的参数设置和运行环境与前述相同)，各算法平均适应值的收敛曲线如图3所示。

从表4可知，对于任意给定的机械臂末端执行器位姿矩阵，HLFOA算法的寻优适应值都可达10-16数量级，说明其对应最优逆解都获得了很高的位姿精度(其位姿误差小于等于10-16)，且HLFOA算法的各项寻优指标都远优于FOA、LGMS-FOA、AE-LGMS-FOA、IFOA及SFOA算法；尽管LGMS-FOA和AE-LGMS-FOA算法也获得较好的最优适应值(其最优适应值分别为10-16、10-12数量级)，但其余优化指标并不理想；由于误差调整因子λ为10-2，可知FOA、IFOA及SFOA算法对应逆解的位置误差最大分量可达102，显然，FOA、IFOA及SFOA算法不能用于解决冗余机械臂的逆运动学问题。