基于虚关节法的3T1R混联机构静刚度特性分析

2021-10-13朱小蓉沈惠平

农业机械学报 2021年9期

朱小蓉吴俣沈惠平

(常州大学机械工程学院, 常州 213164)

0 引言

三平移一转动并联机构具有速度快、精度高、操作性能好等优点，在装配、包装及码垛等高速重复性工程领域应用较为广泛[1-8]。机构刚度反映机构在外载作用下因弹性构件变形引起的末端执行器位姿变化，决定了机构在负载下的定位精度。因此，三平移一转动并联机构的刚度模型已成为评估机构工作性能的重要指标之一[9-12]。

现有的刚度分析方法包括有限元分析法、矩阵结构分析法和虚关节法。其中，虚关节法由GOSSELIN等[13]提出，最初仅考虑驱动关节的柔性，将每一个驱动关节的变形等效为一个单自由度的虚拟关节，经过不断发展，又考虑被动关节、连杆、平台的变形以及一些特定的几何约束和内、外部载荷，因此，虚关节法刚度建模的关键在于如何定义虚拟关节。GOSSELIN等[13]将连杆柔度用刚性连杆和单自由度的虚拟关节串联来代替，并提出分别适用于刚性机构和柔性机构的两种刚度建模方法；PASHKEVICH等[14]考虑连杆和驱动关节的柔性，用6自由度虚拟关节来代替柔性连杆，对几种过约束并联机构进行了刚度建模；PASHKEVICH等[15]考虑被动关节内预加载荷条件，基于虚关节法建立了机构刚度模型，同时考虑外部载荷对机构刚度的影响，提出动态静力控制算法，以补偿外部/内部载荷引起的误差；AMIR等[16]考虑动平台的刚度，分别用集总模型和分布式模型建立3-PSP并联机构的刚度矩阵，并用有限元法评估了模型的精确性；WU等[17]采用实验方法获得直线电机驱动系统的非线性柔度特性，并考虑驱动系统和连杆变形建立了3-PPR并联机构的刚度模型；吕帮俊等[18]将虚关节法与有限元法相结合，采用有限元分析法对驱动杆和万向铰链进行刚度分析，建立了有预载和无预载情况下的机构刚度半解析模型；ALEXANDR等[19]基于虚关节法提出一种并联机构在内、外载荷作用下的刚度建模方法；张俊等[20]利用有限元法得到虎克铰、球铰、转动副部件的刚度矩阵，用虚关节法建立了较高精度的机构刚度模型，有限元验证结果表明，其误差可控制在5%以内；GORGULU等[21]采用虚关节法对一种并联触觉装置进行刚度建模，并就计算精度和计算成本与有限元分析方法进行了比较，从而验证了虚关节法的有效性，可用于触觉装置控制回路的实时控制。

虚关节法将构件分布式变形以虚拟关节模型集中表示，不仅简化了模型，而且物理意义明确、计算量适中，已成为机器人技术领域常用的刚度分析方法。然而，采用虚关节法对混联机构，特别是对含闭合回路或子并联机构的复杂机构进行刚度建模的研究并不多见。

本文采用虚关节法，考虑驱动电机、丝杆螺母副、导轨和运动连杆的变形，建立(3CRR/R)&CRU混联机构的静刚度半解析矩阵，提出线性刚度和角刚度的无量纲化评价指标，分析机构规则工作空间内的静刚度分布。

1 机构描述

本文所研究的(3CRR/R)&CRU混联机构，是由Quadrupteron机构进行结构降耦所得[22]，结构如图1所示。该机构具有耦合度低、运动解耦、工作空间大等特点。

机构由静平台0、中间平台1、末端平台2以及4条支链组成。动平台2，一方面，通过C41R42U43支链直接与静平台0相连；另一方面，通过转动副RD、中间平台1及3条CRR支链与静平台0相连。其中，3条CRR支链满足Ci1∥Ri2∥Ri3(i=1,2,3)，且C11、C21、C31互相正交；4个移动滑块分别安装在间距为L的4个轨道上，通过安装在固定框架上的4个伺服电机驱动丝杠螺母副进行控制；该机构的末端平台2能够实现3个方向的移动以及绕垂直方向轴线的转动。

由图1可知，末端平台2通过RD和U43分别与静平台相连接，故机构可以看成2个子结构并联组成。其中，子结构1为Ci1Ri2Ri3(i=1,2,3)子并联机构与RD串联而成，子结构2为C41R42U43简单支链，其组成单元如图2a所示。

2 基于虚关节法的刚度建模

混联机构静刚度是机构位姿的函数，为简化计算，在建模过程之中，依据该混联机构的结构特点，做如下假设：①不考虑各关节处的摩擦、阻尼和接触变形。②中间平台和末端平台采用M60J碳纤维材料，具有轻量化、高比强度和高比刚度等特点，故不考虑中间平台、动平台的重力及变形影响。③运动杆件采用轻质碳纤维细杆制成，故不计杆件重力；细长杆件的变形，通过在末端添加6自由度虚拟关节来表示杆件的六维柔度变形。④考虑驱动系统的变形，设为单自由度的虚拟扭转关节。⑤导轨变形简化为5自由度的虚拟关节，忽略其轴向线性变形。

基于以上假设，机构所包含的平台、连杆、主动关节和被动关节等构件及其对应的局部柔度虚拟模型如表1所示，对应的该混联机构的柔度组成单元如图2b所示。对该混联机构进行刚度分析，首先应对其2个组成子结构进行刚度建模。

表1 基于虚关节法的构件模型Tab.1 VJM-based modeling of components

2.1 子结构1刚度建模

子结构1由3-CRR子并联机构的末端输出(中间平台1)串联转动副RD而成，因此，应首先建立CRR串联支链的刚度矩阵。

2.1.1CRR支链刚度模型

沿CRR支链的各主、被动关节依次建立局部参考系。为节省篇幅，选取C31R32R33支链为例进行说明，局部坐标系如图3所示。设a、b、c、n为点Ai、Bi、Ci、N在定坐标系xOy下的位置矢量；转动副R32和R33轴线矢量为r1、r2；定坐标系下x、y、z轴矢量分别记为e1、e2、e3。

考虑弹性变形时，中间平台1产生的微小变形，由其组成支链的构件变形和主、被动关节变形引起。对第i条CRR支链，有

δti=Jθiδθi+Jψiδψi

(1)

其中

式中 δti——支链i末端的微分运动，包含三维移动和三维转动

δθi——支链i所有虚关节微分运动构成的矢量

δψi——支链i所有被动关节微分运动构成的矢量

Jθi——虚关节i变形量对末端微分运动的映射，为6×18的矩阵，包括1个1-dof驱动关节、1个5-dof的导轨虚关节、2个连杆的6-dof虚关节

Jψi——被动关节i微分运动对末端微分运动的映射，为6×3的矩阵(3个被动转动副)

根据图3，Jθi、Jψi可表示为

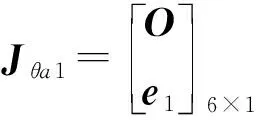
其中w1=a-nw2=b-nw3=c-n

wab=a-bwbc=b-c

式中O——零矩阵

式中，Jθa1、Jθg1、Jθl11、Jθl12分别是驱动变形、线性导轨变形、连杆1和连杆2变形的虚拟关节与末端微分运动的映射。

当支链i末端受力fi时，在平衡状态，设支链中所有虚拟关节的广义力矢量为τθi，被动关节所受力矢量为τψi。由于被动关节受力时产生受迫运动而达到新的静力平衡，因此被动关节不受力，即τψi=0。根据虚功原理，有

(2)

又由胡克定律，有

τθi=Kθiδθi

(3)

其中

式中Kθi——所有虚拟关节刚度矩阵构成的分块对角矩阵

Kθai、Kθgi、Kθli1、Kθli2——第i条CRR支链中1-dof驱动刚度、5-dof线性导轨刚度，以及连杆1和连杆2的6-dof刚度

联立式(1)～(3)可得

(4)

从而，第i条CRR支链刚度矩阵为

(5)

考虑子并联机构所受外力f等于3条CRR支链受力fi的矢量和，且3条CRR支链并联连接于同一中间平台1，从而具有相同的位姿变形δti。因此，子并联机构的刚度为

K0=K11+K12+K13

(6)

2.1.2子结构1刚度模型

分析子结构1的刚度时，将子并联机构视为一个整体，再串接转动副RD，如图4所示。

记串联转动副RD安装的基点矢量为d，末端平台2中心点P的位置矢量为p，转动副RD轴线矢量为r3。子并联机构刚度为K0，引起的末端微分运动映射Jθ1=I6×6(I为单位矩阵)，则子结构1刚度矩阵K1为

(7)

2.2 子结构2刚度建模

子结构2为C41R42U43支链，柔度模型如图2b所示。为构建刚度矩阵，建立图5所示局部坐标系。矢量m、l、s、p分别是点A4、B4、C4、P在定坐标系下的位置矢量；转动副R42轴线的位置矢量为ra，组成U43万向节的2个转动副轴线矢量为rb与rc。

则子结构2刚度矩阵为

(8)

其中

Jθ4=[Jθa4Jθg4Jθl41Jθl42]

式中Jθa4、Jθg4、Jθl41、Jθl42——1-dof驱动变形、5-dof线性导轨变形、连杆1变形和连杆2的6-dof虚拟关节变形与末端微分运动的映射

Kθ4——CRU子结构中驱动关节、导轨关节和两个连杆的刚度矩阵

根据图5所建立局部坐标，可分别表示为

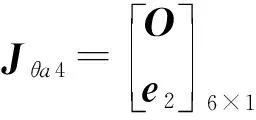
其中w4=m-pw5=l-pw6=s-p

wlm=l-mwsl=s-l

2.3 混联机构刚度建模

由于末端平台2为刚体，则(3CRR/R)&CRU混联机构的刚度矩阵K为

K=K1+K2

(9)

2.4 刚度性能评价指标

混联机构刚度矩阵K是6×6的矩阵，可写成

采用文献[23]提出的矩阵无量纲化处理方法，首先建立机构的静力平衡模型为

(10)

式中M——机构所受力矩

F——机构所受力

Δφ、Δp——机构在该力矩与力作用下产生的微小角变形和线变形

则空间力/力矩又可表示为

(11)

将角变形Δφ与线变形Δp通过线性变换，转换为空间力与力矩的无量纲化参数

(12)

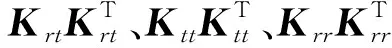
λφ、λp(ωφ、ωp)——力(力矩)作用下无量纲化的线变形与角变形

O3——零矩阵

将式(12)代入式(11)有

(13)

其中

(14)

式中Gf、Gm——3×3的系数矩阵

(15)

显然，kt与kr越大，则机构的线刚度和角刚度性能越好。

kt和kr是机构的位型函数，为评估机构在整个工作空间Ω中的刚度性能，定义全局线刚度和角刚度性能指标Gt和Gr为

(16)

3 混联机构刚度分析

基于上述所建刚度模型，对该机构的虚拟样机进行刚度分析。几何参数如表2所示，为研究结构参数对机构刚度性能的影响，选择合理的杆长，杆件材料采用碳纤维，弹性模量为2.1×105MPa，泊松比为0.3；中间平台半径r=40 mm，末端平台2与中间平台垂直距离h=10 mm；驱动系统采用1FL6024-2AF型直流伺服电机和1605型滚珠丝杆。

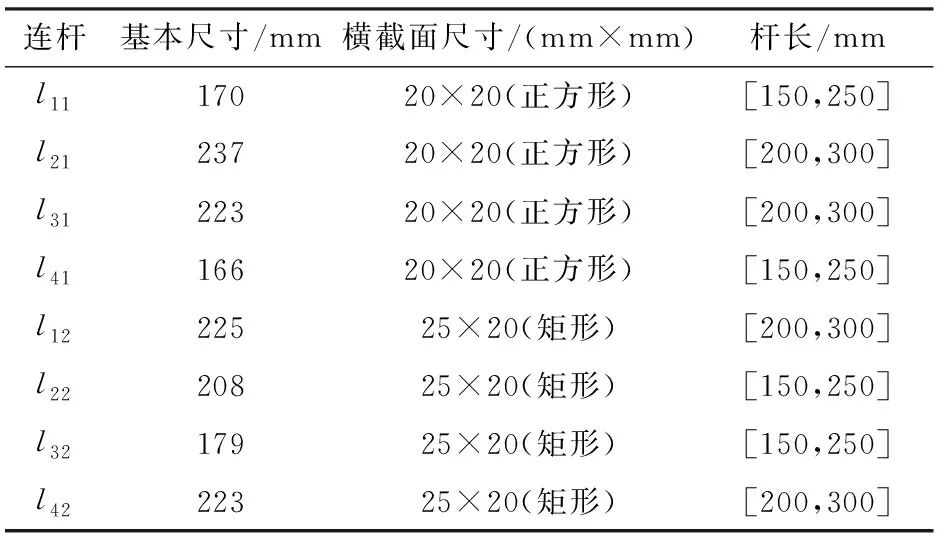
表2 连杆的几何参数Tab.2 Geometric parameters of links

根据式(7)～(9)，计算机构末端平台2中心点P的刚度矩阵。其中，支链组成细长杆件的刚度计算可看成悬臂梁，刚度系数计算式为[24]

(17)

式中A——连杆截面积l——连杆长度

Ix、Iy、Iz——连杆横截面的惯性矩

E——材料杨氏模量

G——材料剪切模量

驱动副的扭转刚度系数计算公式为[25]

(18)

式中Kact——电机驱动器的控制环路刚度系数

kα——电机扭转刚度

d——丝杆螺纹中径

S——丝杆导程ψ——螺纹升角

φv——螺纹当量摩擦角

L——丝杠长度

丝杆采用双支承安装方式，滑块座沿导轨直线移动，结构示意图如图6所示，具体参数见表3。

表3 丝杠传动系统参数Tab.3 Parameters of lead screw system

线性导轨刚度Kθg，采用有限元模型进行分析。利用SolidWorks对滑块和导轨进行实体建模，并在ANSYS中进行有限元分析，得到导轨的3个角刚度kφx、kφy、kφz以及y、z向的线刚度kyy、kzz如表4所示。

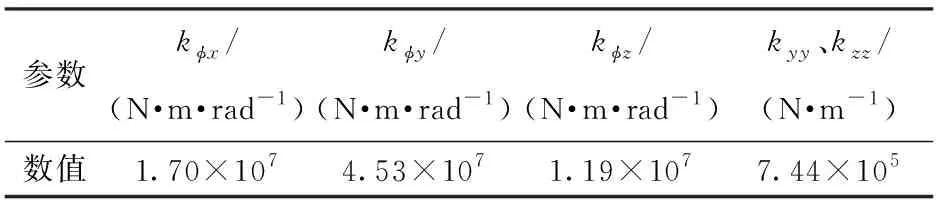
表4 导轨刚度Tab.4 Stiffness of linear guideway

3.1 结构参数对机构刚度的影响

采用单因素控制法，分析支链长度对机构刚度的影响。需要补充说明的是，当单因素变化时，其余参数保持不变。根据式(16)计算不同结构参数下所对应无量纲的全局线刚度Gt和全局角刚度Gr，结果如图7所示。

由图7可得，随着支链1中杆l11与杆l12长度的增加，机构全局线刚度和角刚度会降低。对支链2，杆l21和杆l22的增加会减小全局角刚度，但对全局线刚度的影响很小。支链3中杆l31与杆l32的增加会降低机构的刚度，特别对线刚度的影响较大。支链4的杆长l41与l42对机构线刚度影响很小，但随着支链长度增加会使角刚度减小。

3.2 机构典型位姿下的刚度矩阵

根据表2中杆件基本尺寸，文献[22]进行了虚拟样机设计，得到机构规则工作空间为180 mm×220 mm×170 mm，转角φ∈(-π/2,π/2)，基坐标下工作空间取值范围为X∈[80, 260] mm,Y∈[90, 310] mm,Z∈[100, 270] mm[22]。

取末端平台中心P点的位置为(170, 200, 200) mm，平台姿态角φ=0°，由式(7)～(9)计算出中心点P在静坐标系下的刚度矩阵为

对该刚度矩阵求逆，可得其柔度矩阵C为

为验证上述静刚度模型的精度，在ANSYS Workbench中建立该混联机构有限元模型，并沿x、y、z方向在动平台中心点P处分别施加单位力矩/力，经静力分析得到相应方向的变形，结果如图8所示，得到点P的位置(170, 200, 200) mm，姿态角φ=0时的角变形量为[3.90×10-5, 5.75×10-5,4.78×10-5] rad，线性变形量为[3.19×10-6,2.95×10-6, 4.2×10-6] m。

将ANSYS Workbench仿真得到的结果与理论建模结果进行对比，结果如表5所示。

由表5可知，ANSYS仿真得到的变形量与理论计算之间存在一定的差距，这是由于安装需要，实际杆件模型与理论建模有区别，但最大误差保持在15%以内，可认为满足精度要求。

表5 ANSYS与理论建模的变形量结果对比Tab.5 Comparisons of static stiffness results between ANSYS and theoretical modeling

3.3 工作空间内的刚度分布

采用分层法将工作空间离散成若干个工作平面，再根据式(9)计算各工作平面上任一点所对应的刚度矩阵，其主对角线元素可看成是机构的角刚度和线刚度。限于篇幅，本文仅取末端平台姿态φ=0，中心点z=200 mm的工作平面，绘制180 mm×220 mm工作平面内刚度矩阵的主对角线元素，结果如图9所示。

由图9可得，机构3个方向的刚度均随机构位姿变化。刚度在工作平面内分布较为均匀、无突变，说明机构刚度性能良好。机构x方向的线刚度，沿x方向保持不变，沿y轴方向呈现线性递减趋势；而y方向的线刚度，沿y轴方向不变，沿x轴呈现线性递减趋势，这应该与机构x向和y向的运动输出具有解耦性有关。机构z方向的线刚度，呈现相对于y=x轴线对称的趋势，这可能与机构第1支链与第3、4支链沿斜边对称的布置方式有关，说明支链布局影响机构的刚度分布。

3.4 工作空间内无量纲刚度

据2.4节式(15)提出的无量纲化性能指标，分析z=200 mm，φ=0时，xOy平面内无量纲化的线刚度和角刚度分布，结果如图10所示。

由图10可得，机构线刚度kt比角刚度kr大1个数量级，说明机构的线刚度较高，对抗移动方向上载荷形变能力较高；而角刚度性能一般，承受转矩能力较弱。线刚度kt沿x正方向和y正方向均呈现增加的趋势，但总体分布较为均匀。角刚度kr在工作空间边界处变化较大外，其余分布较为平坦。

3.5 末端姿态角对刚度性能的影响

为评价机构刚度随末端姿态角的变化情况，利用式(15)计算末端平台位置固定但姿态变化时机构的无量纲线刚度kt和角刚度kr，图11分别是末端平台中心位于点(170,200,200)mm、(120,150,200)mm和点(220,250,200)mm的角刚度和线刚度随机构姿态角的变化曲线。

根据式(16)计算机构不同姿态下的全局线刚度Gt和角刚度Gr，图12为z取120、160、200 mm时工作平面内的刚度。

由图12可得，末端姿态变化时，xOy工作平面内全局线刚度Gt几乎不变；但随着z向高度提升，全局线刚度Gt增加，这有利于机构的抓取操作。末端姿态变化时，工作平面内的全局角刚度变化较小，z为120、160、200 mm时的变化范围分别为2.36×104～ 2.43×104、2.48×104～ 2.50×104、2.49×104～2.51×104，刚度一致性较好。