基于一类含极少运动副四支链两转一移三自由度并联机构的五轴混联机器人
2019-07-18许允斗赵云张东胜徐郑和姚建涛赵永生
许允斗,赵云,张东胜,徐郑和,姚建涛,赵永生,*
1.燕山大学 河北省并联机器人与机电系统实验室,秦皇岛 0660042.燕山大学 先进锻压成型技术与科学教育部重点实验室,秦皇岛 066004
少自由度并联机构具有结构简单、制造成本低及控制容易等优点,近年来,它已成为机器人和机构领域的研究热点。在各类少自由度并联机构中,两转一移三自由度(2R1T)并联机构是非常重要的一类机构[1-2],特别是在五轴混联机器人方面得到了成功应用,其在航空航天、船舶等高端制造领域复杂结构件作业方面具有工作空间大且操作灵活的明显优势,目前已得到成功应用为数不多的几款五轴混联机器人产品均是在2R1T并联机构基础上设计的,包括 Tricept[3]、Ecospeed[4]和机器人 Exechon[5]等。
但是现有2R1T并联机构存在支链中被动运动副(非驱动副)数目较多,支链连杆与连接关节也相应增多,而机构整体性能受支链最薄弱的关节或连杆制约,因而运动副数越少机构整体性能越容易得到保证。文献[1,6]分析的3RPS机构,文献[7]分析的3RSR机构,Sprint Z3主轴头所采用的3PRS机构[8],文献[9]综合出的无伴随运动3PRRU机构,文献[10]提出的无伴随运动3UPU对称机构,文献[11]综合得到的3RRRRR机构,它们每条驱动支链中均含有4个被动单自由度运动副,如图1所示。其中U副等效于轴线交于一点的两个R副,由于混联机器人工作空间要求比较大,这里S副一般设计成轴线交于一点的3个R副,注意,这里R、P、S和U分别表示转动副、移动副、球副和虎克铰。组成TriVariant五轴混联机器人的三支链机构2UPS-UP[12]含有的被动单自由度运动副数为12。组成Exechon五轴混联加工中心的2UPR-SPR机构[13],文献[14]综合得到的 UPS-PRC-PU机构(C表示圆柱副),文献[15]分析的UPS-RPU-PU机构,它们含有的被动单自由度运动副数均为10。文献[16-17]提出的主轴头结构(PUS+R)-PRR-PR 及文献 [18]提出的2UPR-RPU机构,含有的被动单自由度运动副数目为9,是目前含有3条支链2R1T并联机构中运动副数最少的两种机构。构成Tricept五轴混联机器人的3UPS-UP机构[19]每条驱动支链中被动单自由度运动副数为5,再加上约束支链的被动运动副,共有被动单自由度运动副18个,如图2所示。但该机构含有4条支链,3条驱动支链关于约束支链对称布置,大幅提高了承载能力。组成TriMule五轴混联机器人的2UPR-UP-UPS并联机构[20]也由4条支链组成,其含有的被动单自由度运动副数减少至14。现有这些2R1T并联机构中,除文献[16-18]提出的两种机构含有的被动单自由度运动副数为9外,其余机构含有的被动单自由度运动副数均在10以上。
此外,从机构受力性能角度分析,四支链2R1T并联机构相对于同类的三支链机构,外部载荷由4条支链共同承受,承载能力得到了提升。因此,本论文拟提出一类具有含极少运动副的四支链2R1T并联机构,为设计出结构紧凑、性能优异的五轴混联机器人奠定理论基础。
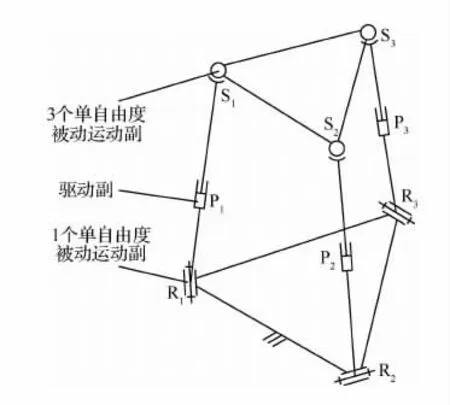
图1 3RPS两转一移三自由度并联机构Fig.1 3RPS 2R1Tparallel mechanism (PM)
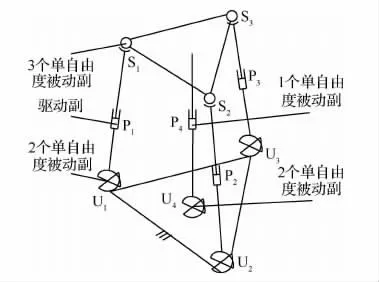
图2 3UPS-UP两转一移三自由度并联机构Fig.2 3UPS-UP 2R1TPM
1 一类四支链两转一移并联机构
1.1 特征描述
本文提出的四支链两转一移并联机构2RPU-UPR-RPR,及 其 倒 置 机 构 2UPR-RPURPR,分别如图3(a)和图3(b)所示。这里以2RPU-UPR-RPR机构为例对2R1T机构特征进行说明,该并联机构由动平台、固定平台、两条RPU支链、一条UPR支链和一条RPR支链组成。RPR支链A2B2的两R副轴线垂直交错,与定平台连接的R副轴线通过UPR支链A4B4的U副中心A4,与动平台连接的R副轴线分别通过两RPU支链A1B1和A3B3的U副中心B1和B3。A1B1和A3B3两支链中U副靠近动平台的转轴与A2B2支链中与动平台连接的R副轴线共线,A1B1和A3B3两支链中与定平台连接的转轴与A2B2支链中与定平台连接的R副轴线相互平行。A4B4支链中U副靠近定平台的转轴与A2B2支链中与定平台连接的R副轴线共线,A4B4支链中与动平台连接的转轴与A2B2支链中与动平台连接的R副轴线平行。定平台A1A3A4和动平台B1B3B4均为等腰三角形,B2、A2分别位于上、下两个等腰三角形的斜边上的中点,且A2A3、A2A4边长分别为a和b,B2B3边长为c,A1P1B1、A3P3B3、A4P4B4支链的初始杆长分别为r10、r30和r40。
为了方便,在定平台A2点建立参考坐标系N:A2-XYZ,在动平台B2点建立运动坐标系n:B2-xyz。经分析,固定坐标系的X轴(标记为r1)和运动坐标系的y轴(标记为r2)总是该机构动平台两个转动自由度的轴线,即该2R1T并联机构存在两条连续转轴[16]。
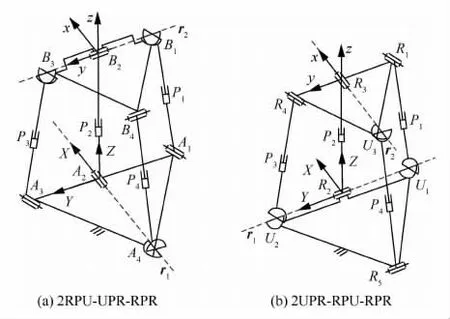
图3 一类四支链两转一移并联机构Fig.3 One type of 2R1TPMs with four branches
1.2 讨 论
目前现有2R1T并联机构中,Tricept五轴混联机器人所采用的3UPS-UP机构[3]和文献[20]提出的2UPR-UP-UPS机构是两类主要的含有4条支链的2R1T机构,其被动单自由度运动副数目分别为18和14。而本文提出的具有四条支链的2R1T机构2RPU-UPR-RPR和2UPR-RPU-RPR,其含有的被动单自由度运动副数仅为12。
2 四支链2R1T并联机构末端极限约束力螺旋系分析
为实现极少运动副机构的设计,这里提出极限约束力螺旋系的定义,它是指使机构真实存在的最多约束力螺旋组合。基于极限约束力螺旋能够实现含极少运动副数目机器人机构的设计。下面分析四支链2R1T并联机构末端极限约束力螺旋系。
根据互易螺旋理论[21-22],并联机构的动平台的转动轴线必须与约束力轴线在同一平面(相交或平行),并且垂直于约束力偶轴线。对于2R1T并联机构,则其末端受到各支链施加的约束力螺旋系最大线性无关组应为一个约束力偶和两个约束线矢力(这里只分析当约束力螺旋系为纯力偶与线矢力的组合的情况),且由于并联机构输出平台受到的约束螺旋系是各支链提供给其约束螺旋系的并集,即
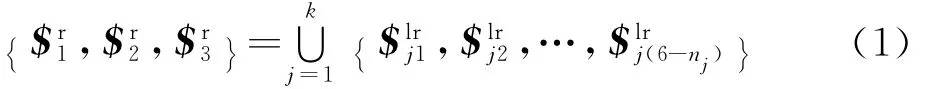
式中:nj表示第j支链单自由度运动副数目;k=3或4。
因而每条支链提供的约束力螺旋系至多包含两个约束线矢力和一个约束力偶,即nj≤3。为保证支链提供的所有约束力螺旋最大线性无关组为一个力偶和两个线矢力,所有支链提供的力偶方向均应一致,由两个平行线矢力产生的力偶方向也必须相互平行且与约束力偶同向。此外,所有支链提供的约束线矢力均应处于同一投影平面内。
对于四支链2R1T并联机构,满足以上要求的约束力螺旋系配置情况很多,比如文献[20]列出的含3个线矢力和多个力偶的情况,本文将研究存在相应2R1T机构真实构型的极限约束力螺旋系(即约束力螺旋系数目达到上限),此时所得机构的运动副数目将达到极限。比如,对于四支链2R1T机构,由式(1)可推断其末端约束力螺旋系至多为线性相关的8个线矢力和4个力偶,但是否真实存在对应的2R1T机构构型还需深入研究。
并联机构输出平台的运动螺旋系是各支链运动螺旋系的交集,对于2R1T并联机构,则有
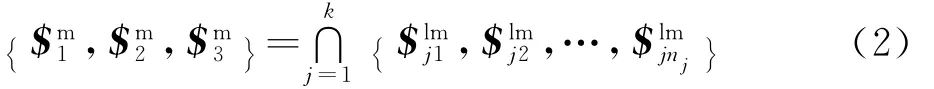
由式(2)可判断每个支链至少含有3个单自由度运动副。事实上,研究2R1T并联机构的极限约束力螺旋系可转化为各支链最少运动副数的求解。这里首先讨论当其中有两条支链含有3个单自由度运动副时,这两条支链运动螺旋系的并集能否得到期望的两转一移自由度。只有当这两条支链形成一个平面六杆闭环机构,它们才可能具有平面的3个自由度,但是为了达到2R1T机构预期的运动形式,这两条支链均不能是平面支链,这说明了该类2R1T机构不可能同时存在两条以上仅含有3个单自由度运动副的支链。因此这里不妨假设各支链最少运动副数情况为:其中一条支链仅含有3个单自由度运动副,其他支链含有4个单自由度运动副。
含3个单自由度运动副支链的基本形式为R1PR3和PU(或UP),如图4所示。R1PR3支链两R副轴线异面,P副轴线垂直于R1和R3轴线,PU支链P副轴线垂直于U副靠近P副的轴线r1。
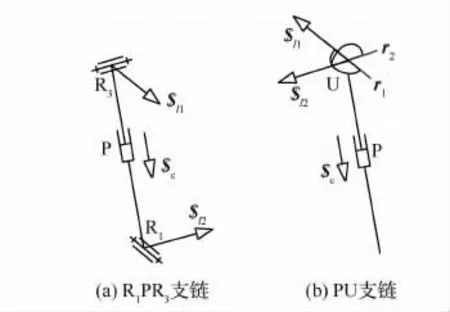
图4 含3个单自由度运动副支链的基本形式Fig.4 Basic forms of kinematic chains with three single degrees of freedom
那么对于任一条含有4个单自由度运动副的支链,其与上述含3个单自由度运动副支链形成单闭环后必须具有预期的两转一移自由度。只有当7个单自由度运动副形成平面机构才最多具有4个自由度,但是显然三自由度支链和四自由度支链均不是平面支链,对于三自由度支链有两个运动副轴线(P和R1轴线或P和U副的r1轴线)位于一平面(记为平面Ⅰ)内,另一转动副(R3副)轴线不位于该平面内,对于四自由度支链至多有3个运动副轴线位于一平面内(记为平面Ⅱ),且至少有一转动副轴线不位于该平面内。那么,只有当两支链运动副轴线形成的平面Ⅰ和平面Ⅱ重合,从而两支链处于该重合平面内的5个运动副形成一个平面机构,具有两个自由度,且两支链剩余的两转动副轴线重合,得到另外一个转动自由度,此时两支链形成的闭环机构具有最多预期的3个输出自由度。这样的典型四自由度支链包括R4R5R6R7、R4PR6R7支链等,如图5所示,其中R4、R5、R6三运动副轴线或R4、P、R6三运动副轴线处于一平面内。
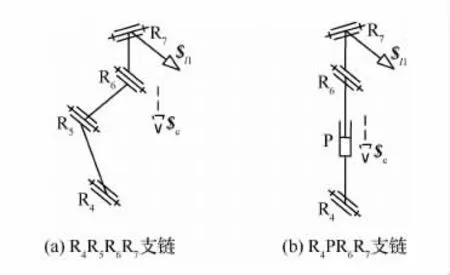
图5 含4个单自由度运动副支链的典型形式Fig.5 Typical forms of kinematic chains with four single Degrees of Freedom (DoF)
其中四自由度支链R4PR6R7与三自由度支链R1PR3形成的单闭环机构如图6所示,则另一条四自由度支链也须有一个转动副与R1轴线重合,剩余3个运动副处于同一平面内,且与R1PR3支链中P和R3副形成一平面机构。
因此,以上过程表明了当四支链2R1T各支链最少运动副数为以下情况时:其中一条支链仅含有3个单自由度运动副,其余支链含有4个单自由度运动副,可能存在真实的构型。此时,三自由度支链提供的约束力螺旋系为2个约束力和1个约束力偶,四自由度支链提供的约束力螺旋系为1个约束力和1个约束力偶,所以可假设四支链2R1T的极限约束螺旋系为5个约束力和4个力偶,其中4个力偶同向,5个线矢力需分布在同一投影面内,根据以上分析过程,这样的5个线矢力布置情况如表1所示,即3个线矢力平行,另外2个线矢力也平行且与前3个异面,另外,前3个线矢力形成的平面和后2个线矢力形成平面相互平行且垂直于力偶方向。
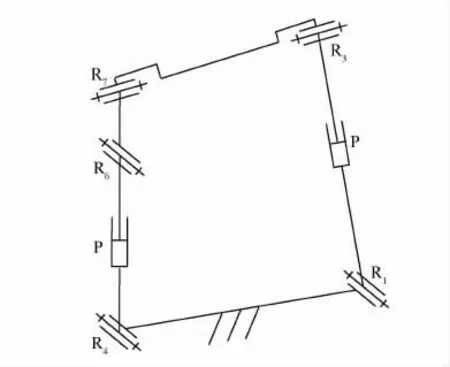
图6 R4PR6R7-R1PR3单闭环三自由度机构Fig.6 Single closed-loop 3-DoF mechanism of R4PR6R7-R1PR3
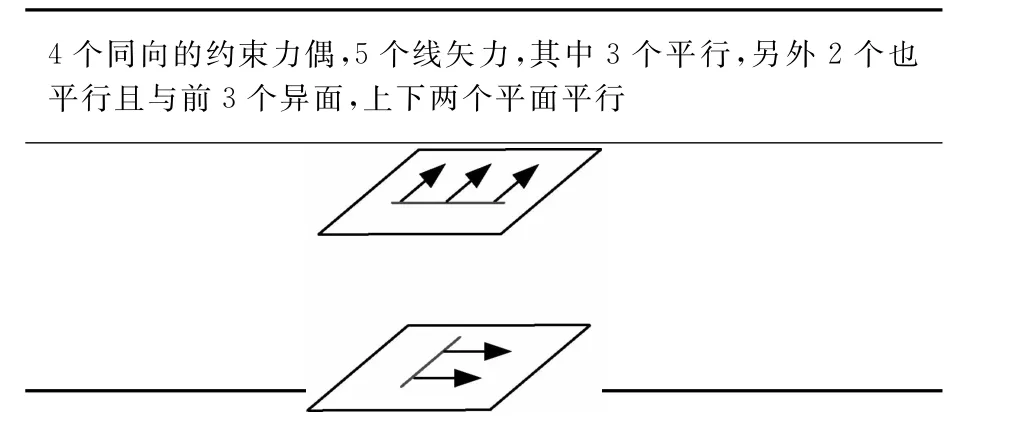
表1 四支链2R1T并联机构末端受到的极限约束力螺旋系Table 1 Ultimate constraint wrenches exerted on moving platform of 2R1TPMs with four branches
而本文提出的四支链2R1T并联机构,其中一条支链为三自由度支链,另外3条支链为四自由度支链,而且经过分析该机构能够实现预期的两转一移运动,所以证明了表1所列即为四支链2R1T并联机构末端受到的一种极限约束力螺旋系,而本文提出的四支链2R1T并联机构即为含极少运动副的四支链2R1T并联机构。
基于上述极限约束力螺旋,采用基于螺旋理论的约束综合法可以综合出一系列其他新型含极少运动副四支链2R1T并联机构,具体流程详见图7。限于篇幅,具体的型综合过程不再详述。
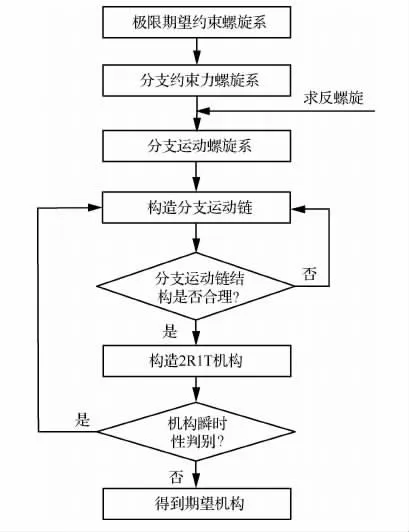
图7 极少运动副四支链2R1T并联机构型综合流程Fig.7 Type synthesis process of four-branched 2R1T PMs containing extremely few kinematic joints
3 在五轴混联机器人方面的应用
3.1 混联机器人的构造
如图3(a)所示的2RPU-UPR-RPR四支链2R1T机构,结构对称性较好,它相对于Tricept机器人的3UPS-UP四支链2R1T机构,关节数目减少了6个,结构刚度和精度更加容易得到保证。机构2RPU-UPR-RPR一条转轴分布在靠近定平台位置(r1),而另一条分布在靠近动平台位置(r2),动平台绕r1的转动可以实现一个水平方向的位置调整,如图8所示,绕r2的转动可实现动平台一个水平方向上的方位调整,如图9所示。因此,基于文献[15]提出的五轴混联机器人机构构造原则,在动平台上方添加一个单自由度摇摆头实现另一水平方向的方位调整,并将并联机构模块安装在一单自由度移动工作台实现另一水平方向位置的调整,由此构造得到的五轴混联机构加工机器人构型方案如图10所示。

图8 五轴混联机器人r1转轴具体位置Fig.8 Specific position of r1on the five-axis hybrid robot
图9 五轴混联机器人r2转轴具体位置Fig.9 Specific position of r2on the five-axis hybrid robot
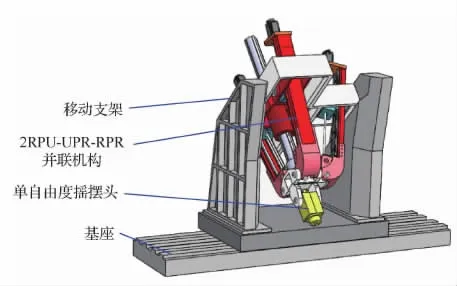
图10 基于2RPU-UPR-RPR机构设计的五轴混联机器人Fig.10 A five-axis hybrid robot based on 2RPU-UPR-RPR mechanism
3.2 混联机器人位置正反解模型求解
下面以上述设计的五轴混联机器人为例进行位置正反解分析,其机构简图如图11所示。
混联机器人的位置模型求解要比单纯并联机器人或串联机器人均要复杂,因为其同时存在并联机器人位置正解与串联机器人位置反解的难题。由于组成本文所提出混联机器人的2R1T并联机构2RPU-UPR-RPR存在两条连续转动轴线,使得其位置正解得到了大为简化,下面首先分析该并联机构的位置反解。
根据机构几何特点[15],Ai点位置矢量在{N}系中可表示为
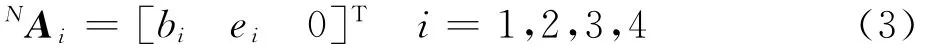
式中:e4=b1=b2=b3=0。
Bi点位置矢量在{n}系中可表示为
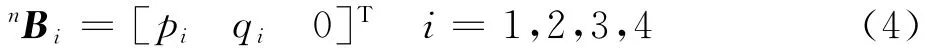
式中:q4=p1=p2=p3=0。
则Bi点位置矢量在{N}中可表示为

式中:NnR为{n}系相对于{N}系的旋转变换矩阵;NPn0= [x y z]T为{n}系原点B2在{N}坐标系下的位置矢量。
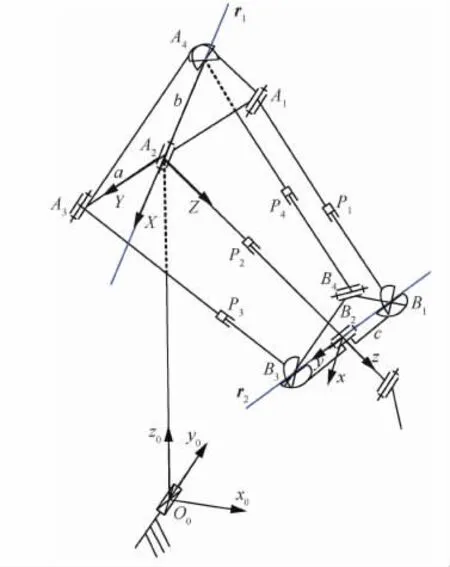
图11 基于2RPU-UPR-RPR设计的五轴混联机器人机构Fig.11 Mechanism of the five-axis hybrid robot based on 2RPU-UPR-RPR mechanism
由前面分析可知,2RPU-UPR-RPR并联机构具有一个移动自由度和两个转动自由度,而且两个转动自由度具有连续轴线,故而动平台可以通过以下三次变换得到最终的任意位姿:首先绕X轴旋转θ2;然后沿z轴移动d30;最后绕y轴旋转θ4,则描述运动坐标系{n}相对参考坐标系{N}位姿的齐次变换矩阵NnT为
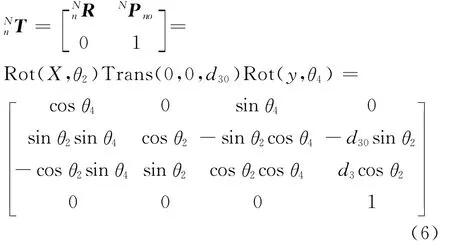
如果已知动平台位姿矩阵nNT,则动平台上各铰链点位置矢量可由式(5)求出,则3个分支杆的长度可以求解得到:
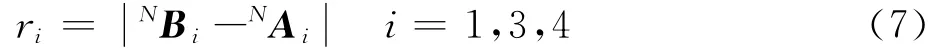
此式即为并联机构的位置反解。
由于2RPU-UPR-RPR机构动平台位姿可通过上述3次连续变换得到,所以该机构可等效为R、P和R副3个运动副组成的串联机构,则整个混联机器人机构可等效为P1R1P2R2R3串联机构,其运动副中心分别记为P1、R1、P2、R2和R3,如图12所示,这将大大简化混联机器人位置建模过程。
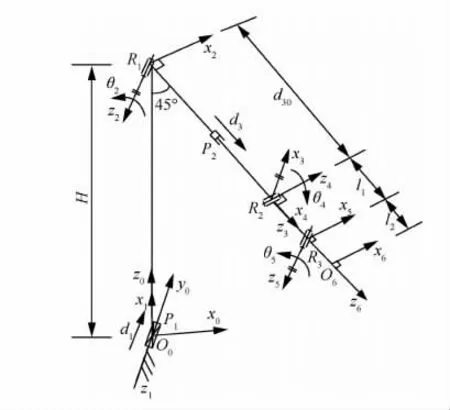
图12 混联机器人的等效串联机构简图Fig.12 Schematic diagram of equivalent serial mechanism of hybrid robot
首先建立混联机器人运动学正解方程,即给定机器人各关节变量,求解机器人末端杆件的位置和姿态。根据图12中建立的连杆坐标系可得五自由度等效串联机构P1R1P2R2R3的D-H连杆参数和关节变量,如表2所示。

表2 等效串联机构PRPRR的D-H连杆参数及关节变量Table 2 D-H parameters and joint variables of equivalent serial mechanism PRPRR
由D-H法[23]可知,相邻关节坐标系之间的齐次变换矩阵为
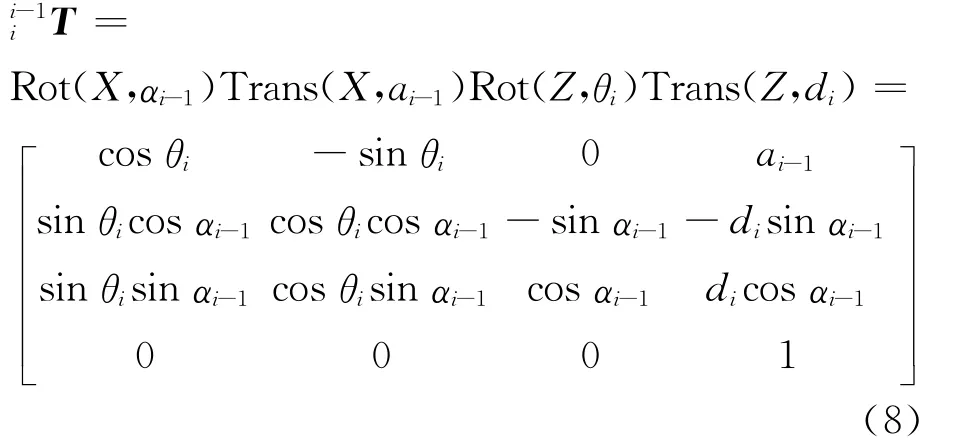
n自由度串联机器人末端连杆坐标系相对于基座坐标系的齐次变换矩阵表达式为

将表2中的关节参数代入式(8)可求得各相邻坐标系的齐次变换矩阵,然后将求得结果代入式(9),即可得PRPRR串联机构的末端位姿矩阵表达式为

式中:d0为初始状态机器人动平台与定平台之间的距离;d1为P1副的输入位移;H为中心点P1和R2之间的距离;d3为P2副的输入位移;d30=d0+d3,表示动平台和定平台之间沿动系{n}z轴方向的实际距离;l1为中心点R2和R3之间的距离;l2为中心点R3和机器人末端O6之间的距离;ci=cosθi;si=sinθi。
下面建立混联机器人的位置反解模型。
首先根据加工工件所需刀具姿态与位移,可以设定等效串联机构PRPRR末端连杆在{0}系下表示的位置和姿态矩阵为
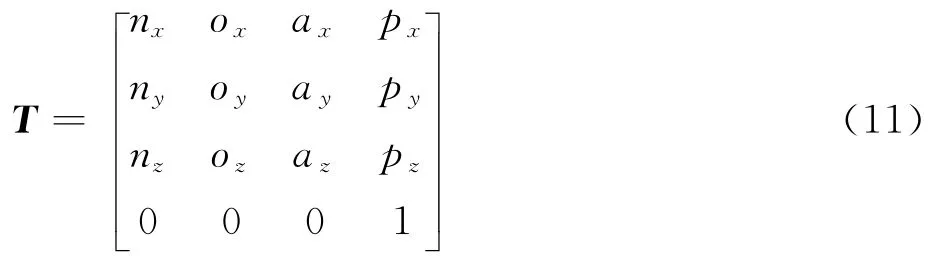
根据上述给定的串联机构末端位姿矩阵,求解串联机构各个关节变量输入值。根据式(10)和式(11)中对应元素相等可得

式中:C=(px-axl2)/(-pz+azl2+H);k11=k(c2-s2);k12=k21=k(c2+s2);k22=-k(c2-s2)。
因此,当给定加工工件所需的刀具姿态与位移后,通过式(13)即可求解得到混联机器人等效串联机构各关节变量输入值,然后将θ2、θ4和d3的值代入并联机构的位置反解模型,即式(7),就可得到并联机构各驱动支链的输入值ri(i=1,3,4),至此,已建立混联机器人完整的位置反解模型。
3.3 算 例
3.3.1 球面加工轨迹的实现
如图13所示,假设拟加工工件的轨迹为一球面,设球面半径为R,令刀头当前所加工圆轨迹的半径为r,则工件球心到加工圆心的距离为m=,且该球心到机床坐标系{0}的x0O0y0平面的距离为h,球心在该坐标系x轴坐标为x0,在y轴的坐标为0,当前加工点与圆心连成的直线与y轴的夹角为α。
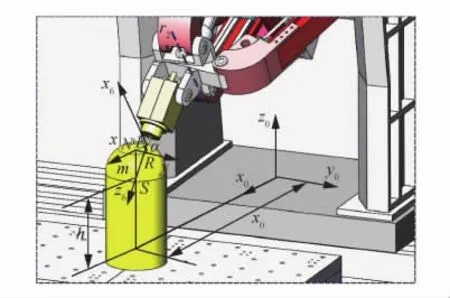
图13 工件拟加工轨迹Fig.13 Processing trajectory on workpiece
则当前加工点的位置坐标为
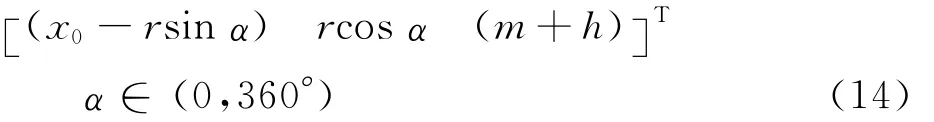
这里要求加工时刀具法线要与工件加工点切平面垂直,所以刀具的指向应为

因为加工件固定不动,故在任意时刻刀具和加工件在的{0}系的x、y、z坐标相同,则{6}系坐标原点在{0}系下x、y、z坐标分别为

将式(15)和式(16)代入式(13)可得
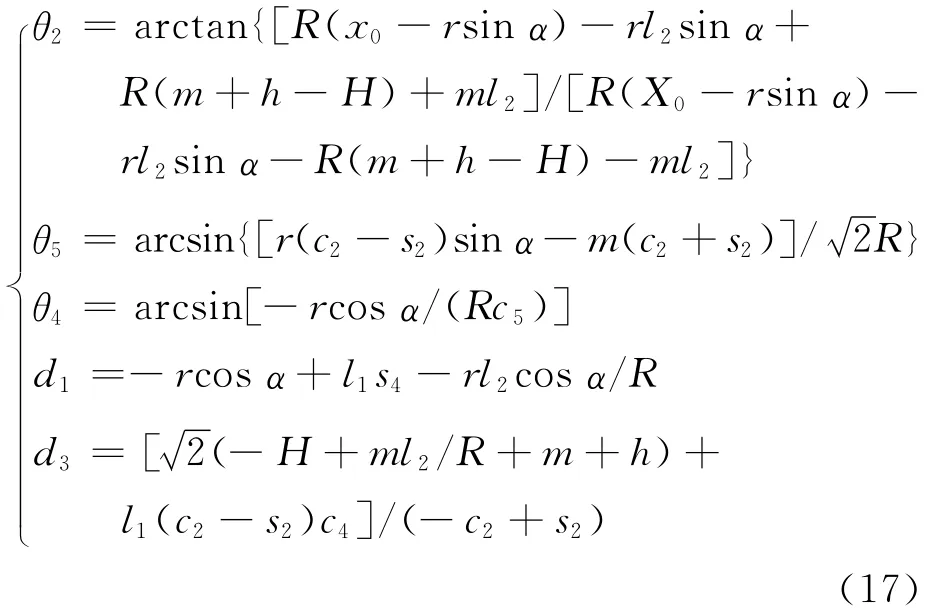
将求得的θ2、θ4和d3代入式(6),可得
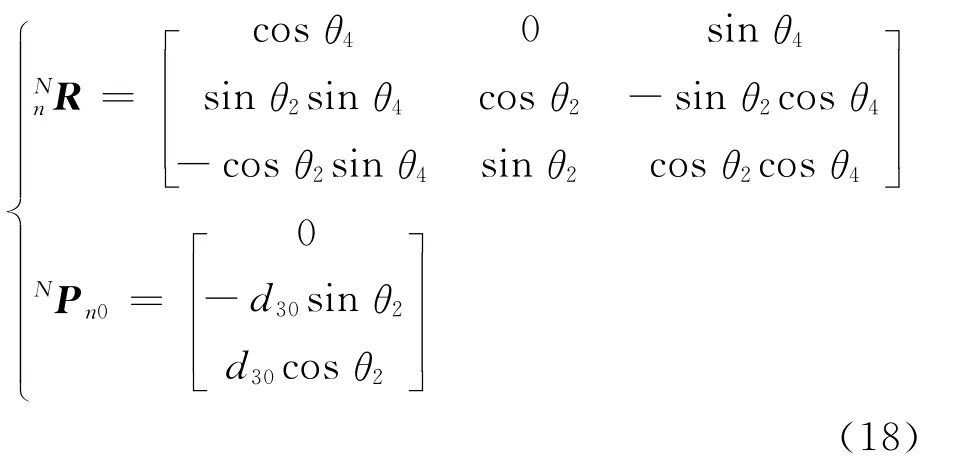
代入式(5)和式(7)可求得并联机构3个驱动杆的输入位移为
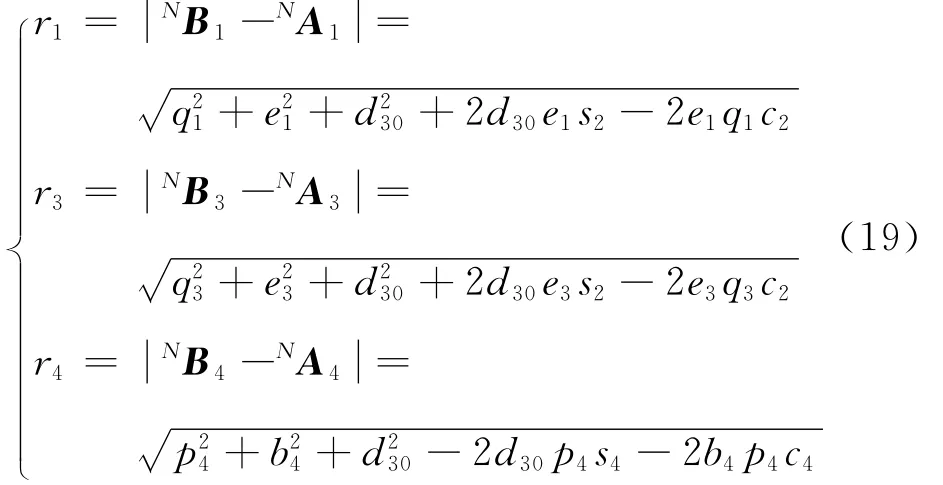
3.3.2 仿真验证
给定一组具体的混联机器人的结构物理尺寸参数和工件加工轨迹参数,如下:a=521.68mm,b=664.59mm,c=302.20mm,上下平台的两个顶点三角形相似,三支分支杆的初始长度r10=r30=1 186.94mm,r40=1 210.79mm,l1=299.95mm,l2=433.17mm,R=200mm,r=120mm,m=160mm,h=600mm,H=2 090mm。两平台初始距离d0可根据机器人结构参数求得为1163.25mm,将具体参数代入式(17)可得
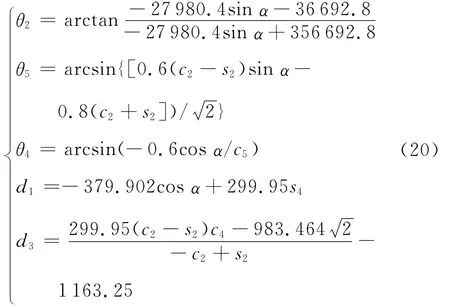
则将反解计算结果代入正解方程,可求解得基于2RPU-UPR-RPR机构混联机器人末端刀具的指向与位置轨迹。图14所示为刀具方位轨迹,从图中可以发现该指向与前面直接根据加工工件轨迹得到的刀具指向是完全一致的。加工工件位置轨迹是由机器人机构末端位置决定的,由此得到的工件位置轨迹如图15所示,从图中可以看出工件轨迹为一个圆,且其半径为120mm,该工件轨迹与前面给定的预加工工件轨迹是完全一致的。
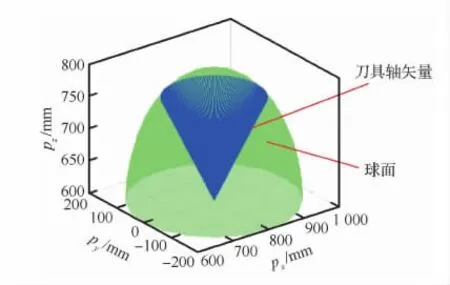
图14 刀具方位轨迹Fig.14 Path of tool’s direction
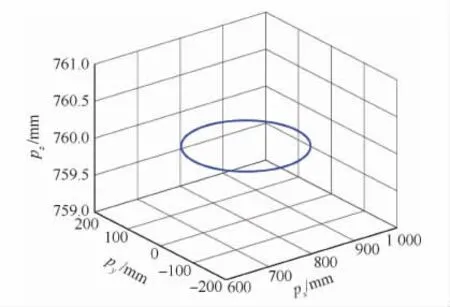
图15 工件加工轨迹Fig.15 Processing path of workpiec
前面分析过程充分说明了该混联机器人可实现工件复杂曲面的联动加工,同时也验证了建立的该混联机器人位置模型是正确的。
4 结 论
1)首次提出了一种极少运动副四支链2R1T并联机构,其含有的被动单自由度运动副数仅为12,与现有同类机构相比均要少。
2)提出了极限约束力螺旋系的概念,基于螺旋理论约束螺旋与运动螺旋之间的对偶关系,论证得到了四支链2R1T并联机构的一种极限约束力螺旋系,证明了所提出的机构是目前同类机构中单自由度运动副最少的,有益得补充了并联机构学理论。
3)基于含极少运动副四支链2R1T并联机构构造了一类五轴混联机器人,求解得到了该混联机器人位置反解的显示解析表达式,并以球面轨迹为例验证了五轴混联机器人机构构型的可行性以及反解算法的正确性。该混联机器人单自由度运动副数目少,具有较大的应用前景。
