基于可变油膜刚度系数的船舶推进轴系模态仿真与分析

金尚崇， 孟文杰， 陈宁宁， 温小飞

(1.舟山市船舶检验中心， 浙江 舟山 316000; 2.浙江海洋大学 船舶与海运学院， 浙江 舟山 316022)

0 引 言

船舶推进轴系是保持船舶安全运行的重要机构，油膜的形态和动力学特性会对其运行状态产生重大影响，对轴承油膜进行研究是解决船舶推进轴系问题的关键。目前，油膜动力学基础理论已广泛应用于碰撞摩擦分析、轴系校中和轴系振动计算等领域中。在碰撞摩擦分析方面：吴敬东等考虑刚度的各向异性，分析了船舶轴系单方向刚度

k

发生变化时,轴承动力学特性的变化情况；李成英等对非线性局部摩擦力与油膜力进行耦合，分析了不同转子系统参数发生变化对转子混沌运动状态的影响。在轴系校中方面:闫小伟在对轴系进行合理的校中计算的基础上，提出了考虑艉管后轴承润滑油膜特性的轴系动态校中方法；蔡保刚和温小飞等将油膜动力学理论与船舶轴系校中理论相结合，提出了船舶推进轴系轴承稳态负荷计算模型和方法，用其研究了轴承油膜形态与轴系轴承稳态负荷之间的关系。在轴系振动计算方面:李小军等考虑陀螺效应的影响，在模态分析中研究了单方向艉轴承刚度变化对轴系回旋振动的影响；陈班班和NGO等在船舶轴系临界转速和模态特性研究中引入变轴承刚度方法，讨论了油膜动力学特性参数对船舶轴系模态特征量的影响。

目前，对轴系模态的分析研究大多只考虑单方向油膜刚度变化对轴系的影响，未考虑多方向油膜刚度变化对轴系的影响。本文综合考虑轴承4个方向的可变油膜刚度系数,对船舶推进轴系进行仿真，精确计算船舶推进轴系主要阶次模态的特征频率、振型和特征量的变化，评价轴系的安全性。

1 数学模型

以经典动力学基本原理和有限元方法为基础，建立船舶推进轴系运动方程，有

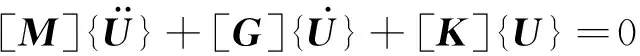
(1)

单元系数矩阵[]和[]的计算公式为

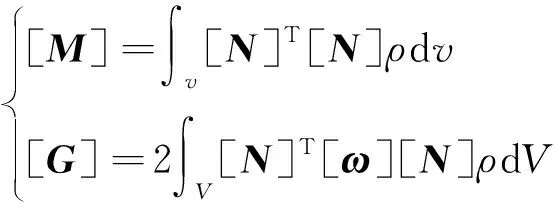
(2)

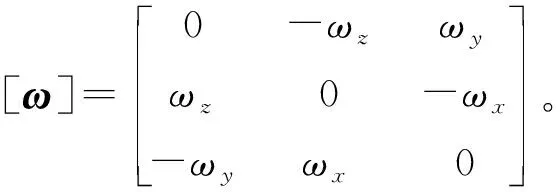
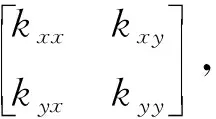
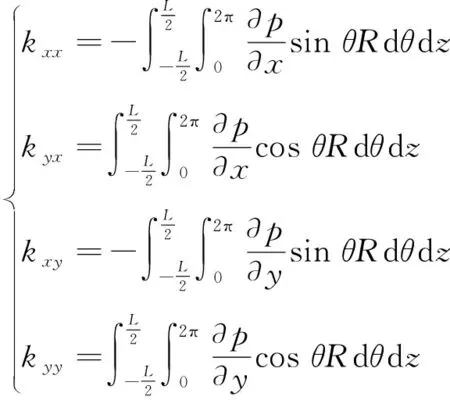
(3)

式(3)中：

k

、

k

、

k

和

k

分别为4个方向的油膜刚度系数；

L

为轴承长度；

p

为油膜压力；

θ

为角度；

R

为轴颈半径。

2 仿真对象

以某64 000载重吨散货船为仿真对象，其主要参数：总长为199.90 m；垂线间长为194.50 m；型宽为32.26 m；型深为18.50 m；设计吃水为11.30 m；载重量为63 800 t；设计航速为14.00 kn。船舶推进系统主要参数：船舶主机为MAN B&W二冲程低速柴油机5S60ME-C8.2，额定功率为8 050 kW，额定转速为89.0 r/min；螺旋桨为5片桨叶的定距桨，桨径为6.70 m，右转向。船舶推进轴系包含1个螺旋桨轴、1个中间轴、1个中间轴承和1个艉轴承，其布置示意见图1，轴承主要参数见表1。

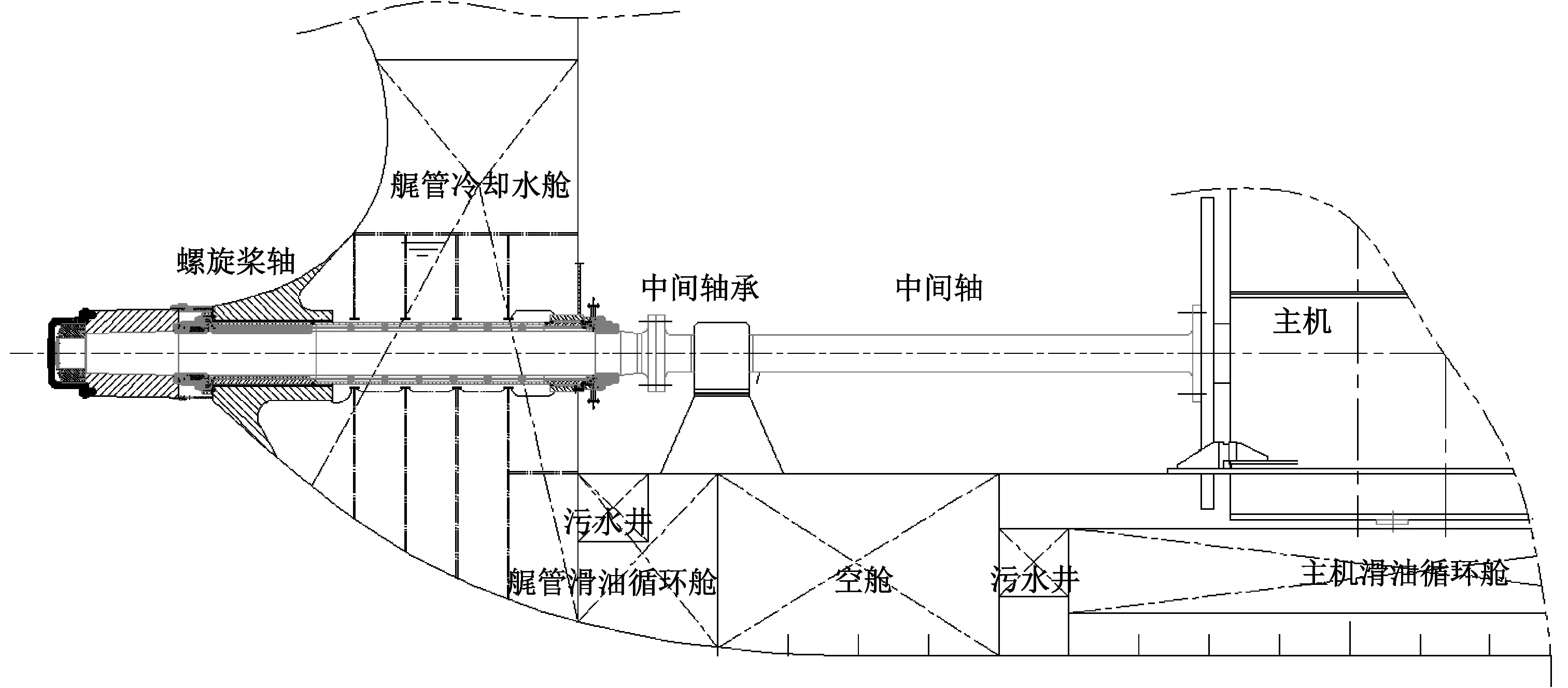
图1 船舶推进轴系布置示意

表1 推进轴系轴承主要参数

3 有限元模型

根据模态分析系统和仿真对象的结构特点，采用BEAM188梁单元将螺旋桨轴、中间轴和主机曲轴作为均质梁处理，并对其进行网格划分，艉轴承、中间轴承和主轴承均采用COMBIN14单元简化为几个圆盘，圆盘的一端与轴承对应节点相连，另一端为固定端，进行全约束，轴中心与圆盘中心在同一条直线上，艉轴承和中间轴承的刚度系数见表2。将螺旋桨作为集中质量处理，螺旋桨的桨毂部分通过适当延长艉轴长度模拟，螺旋桨及附连水的质量和转动惯量较大，采用mass21质量单元，施加在螺旋桨几何中心位置。经上述操作之后得到的船舶推进轴系有限元模型见图2。

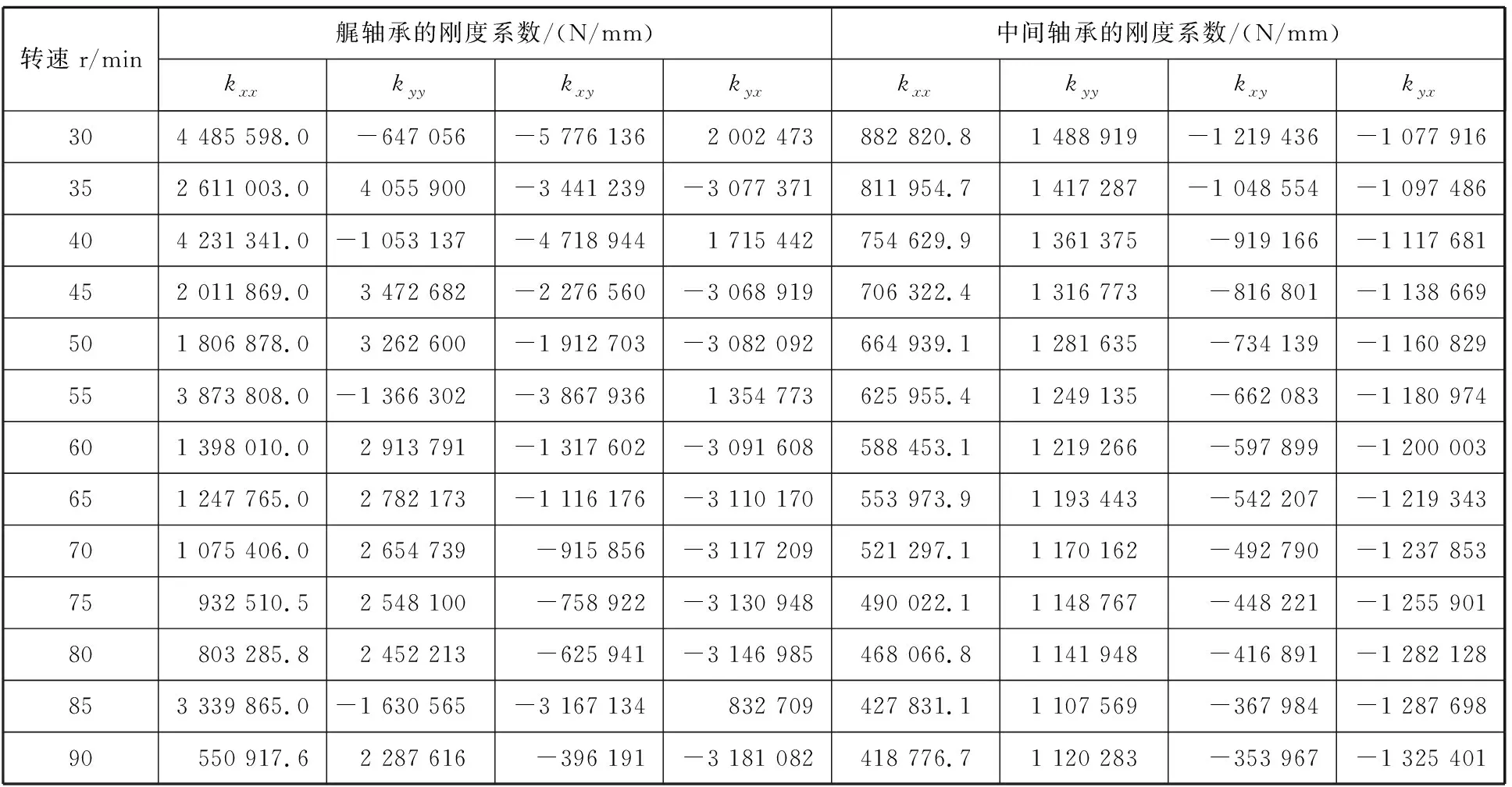
表2 艉轴承和中间轴承的刚度系数

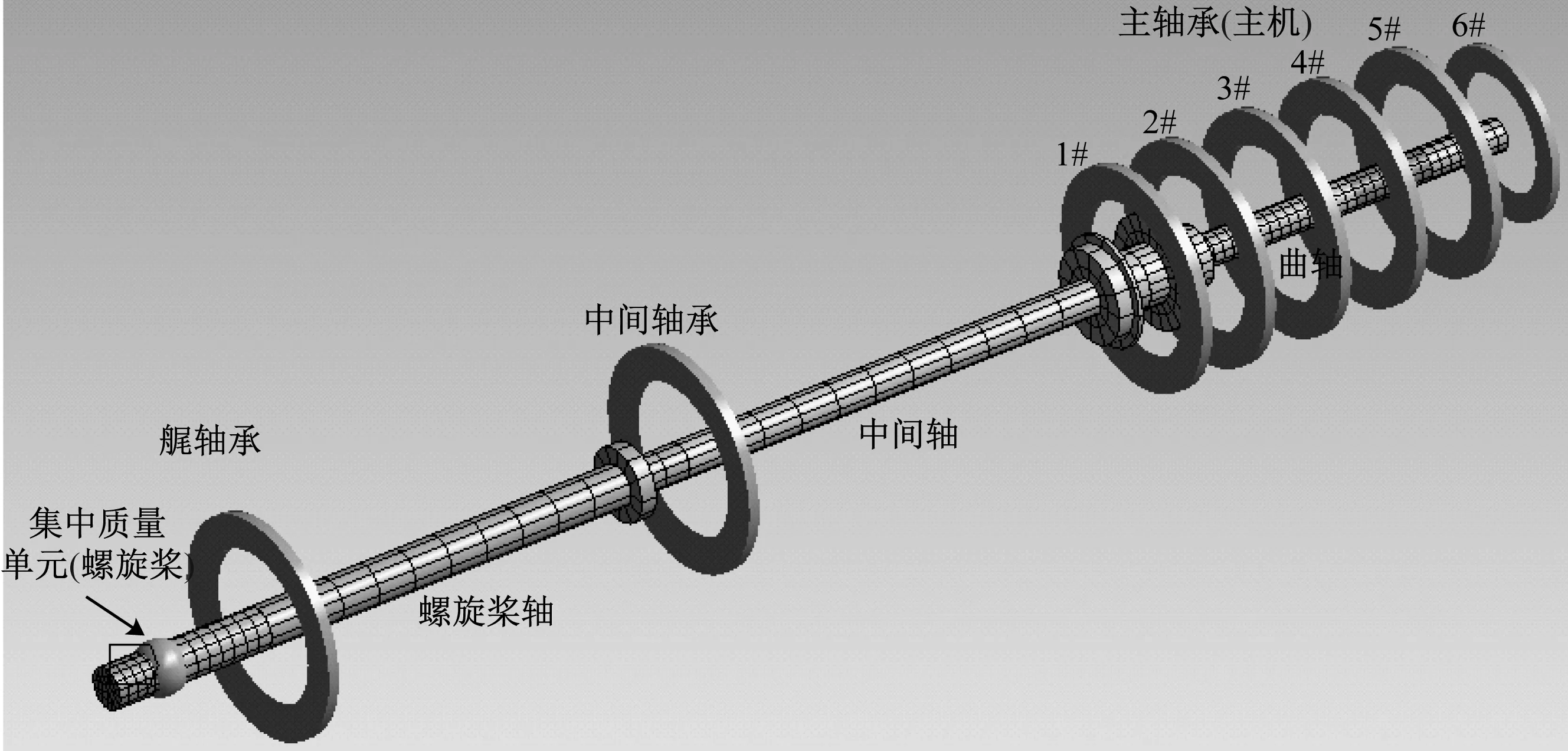
图2 船舶推进轴系有限元模型

4 仿真分析与讨论

船舶推进轴系的模态特征一般以模态振动特性参数和振型图等形式描述。虽然实际分析对象是无限维的，其模态应具有无穷阶(“阶”是指由小到大排列的系统模态频率序号)，但因主导阶次通常集中在前几阶，主要选择前10阶模态进行推进轴系模态特性分析。

4.1 模态频率

船舶推进轴系的模态频率可根据轴旋转方向的不同分为正向和逆向2种，同时还存在部分无法判定方向的微小频率，此部分频率的量级一般为10，不对其进行统计和分析。为区别方向，规定逆向频率用“*”标识，不作任何标识的频率为正向频率。船舶推进轴系各阶模态频率理论值见表3，其中：模态频率计算值分布在3～10阶范围内，1阶模态频率和2阶模态频率为微小频率，不对其进行统计分析；正向频率主要有4阶、5阶、8阶和10阶模态频率，逆向频率主要有3阶、6阶、7阶和9阶模态频率，其中5阶模态频率保持不变，其余模态频率均随转速的变化而变化。船舶推进轴系的模态频率随轴转速的变化曲线见图3，其中L1和L2将变化情况划分为2个区(I区和II区)。在I区，模态频率随着轴转速的变化而发生较大变化；在II区，近似认为模态频率的变化可忽略。由此可得，在考虑油膜动力学的影响时，在高阶低转速区需重点考虑船舶推进轴系模态频率的变化，在其他区域应将模态频率取为定值。

表3 船舶推进轴系各阶模态频率理论值

图3 船舶推进轴系的模态频率随轴转速的变化曲线

4.2 模态振型

根据模态分析目标和主机激励等重要影响因素，主要对正向4个阶次的频率对应的振型特征进行分析，包括总体振型、横向分量振型和垂向分量振型。

4.2.1 总体振型

船舶推进轴系总体振型见图4。由图4可知：4阶模态的最大总体变形量为0.290 480 mm，出现在轴系尾部；5阶模态的最大总体变形量为0.561 060 mm，出现在中间轴与曲轴连接的位置；8阶模态的最大总体变形量为0.408 750 mm，出现在中间轴的中前段位置；10阶模态的最大总体变形量为0.397 510 mm，出现在螺旋桨轴的前段位置；轴系各轴承的位置受约束条件的影响，总体变形量均相对较小。结合船舶艉轴艉管装置的几何结构的约束特点，在螺旋桨轴位置发生的最大变形量潜在安全风险较大，故在船舶设计阶段需重点考虑其影响，防止艉轴承出现异常磨损。

a) 4阶模态

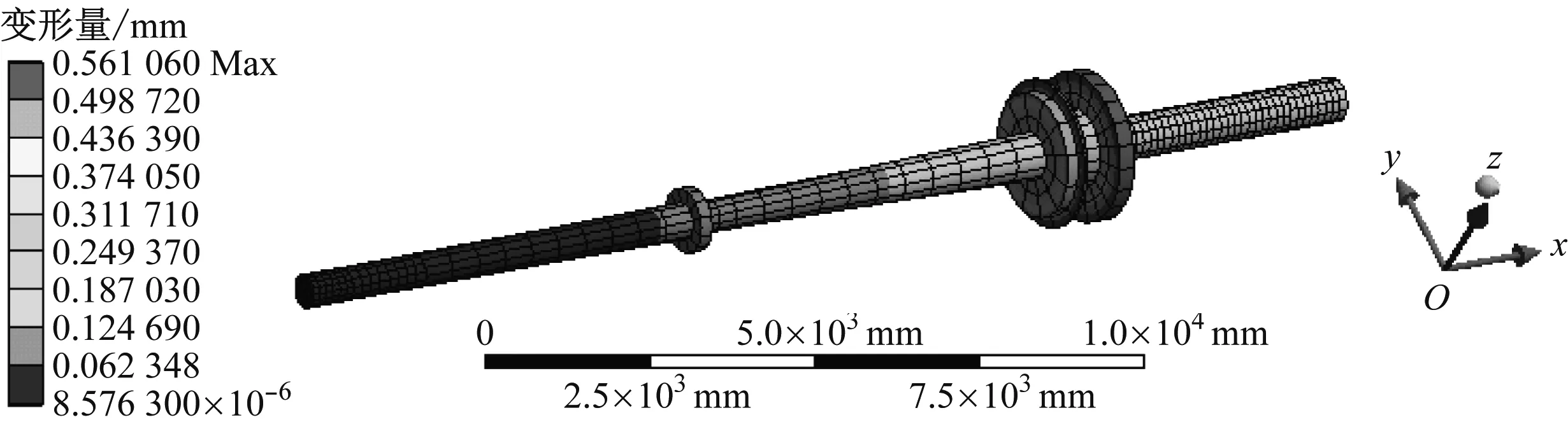
b) 5阶模态

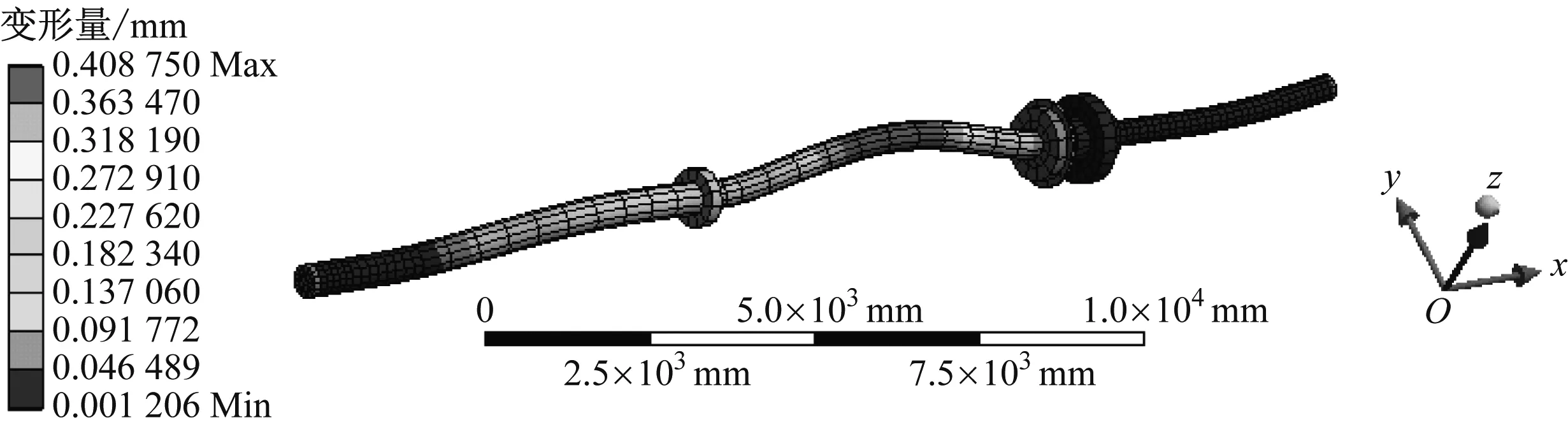
c) 8阶模态

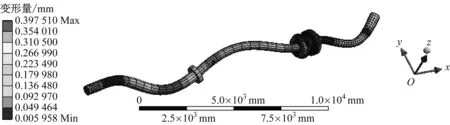
d) 10阶模态图4 船舶推进轴系总体振型

4.2.2 横向分量振型

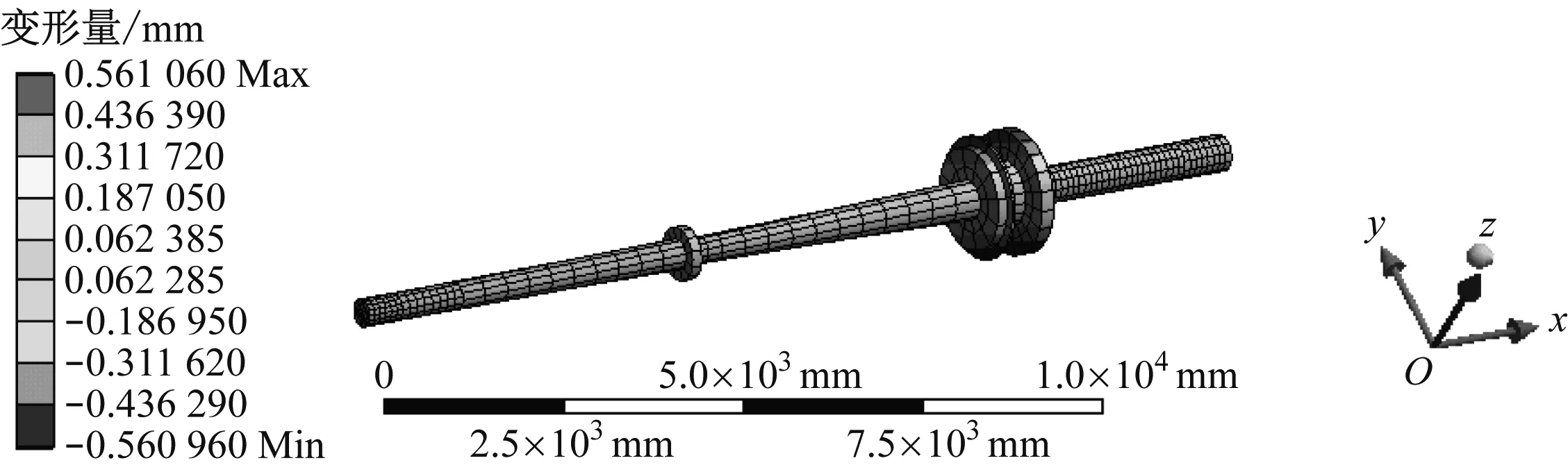
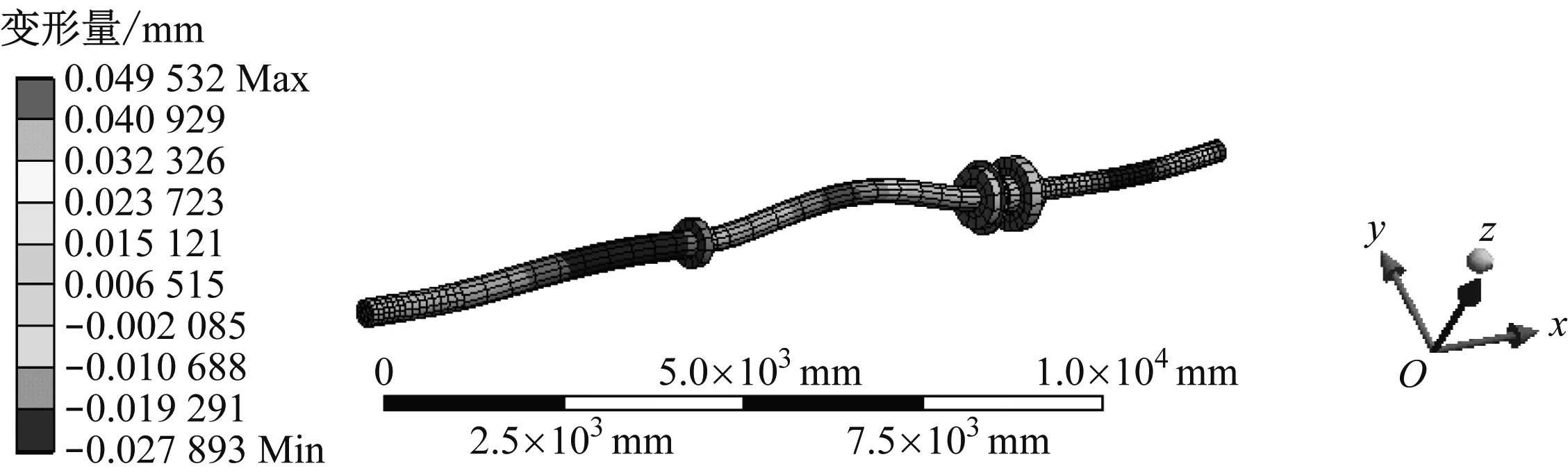
对船舶推进轴系总体振型进行横向分解之后可得到各阶模态的横向分量振型见图5。由图5可知：4阶模态的横向变形量范围为-0.065 401～0.158 320 mm，最大横向变形量出现在轴系尾部；5阶模态的横向变形量范围为-0.560 960～0.561 060 mm，最大横向变形量出现在中间轴与曲轴连接的位置；8阶模态的横向变形量范围为-0.027 893～0.049 532 mm，最大横向变形量出现在中间轴中段位置；10阶模态的横向变形量范围为-0.225 110～0.336 660 mm，最大横向变形量出现在轴系前端位置。比较各阶模态的横向变形量可得：当模态振动为5阶时，横向变形量最大，在船舶设计阶段需重点校核其影响，并在运行管理过程中进行监控。

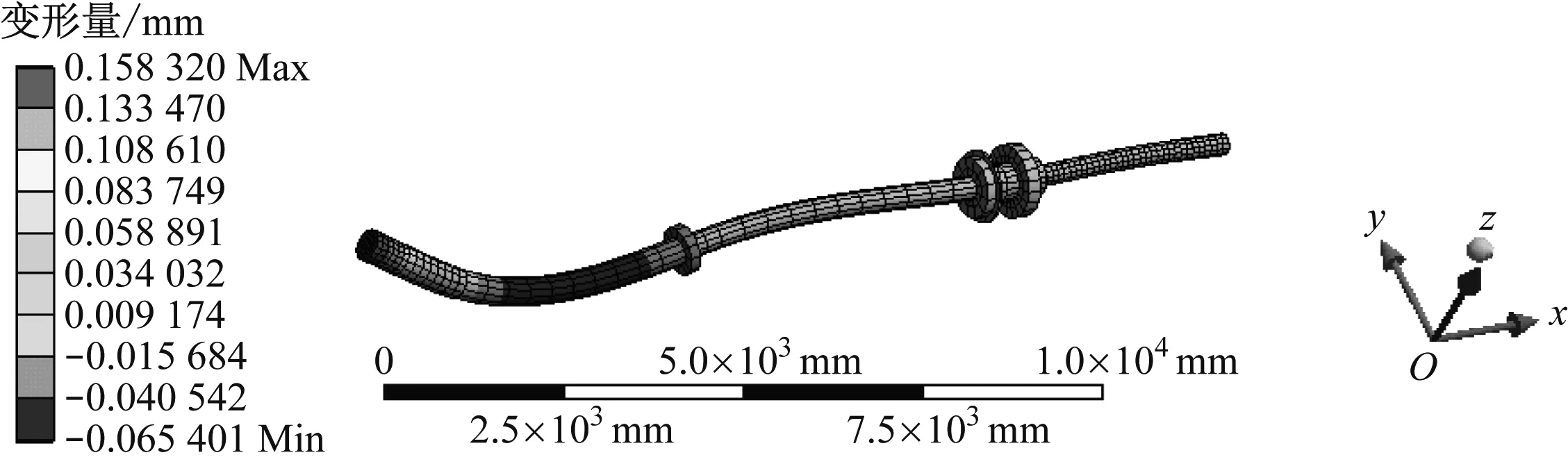
a) 4阶模态

b) 5阶模态

c) 8阶模态

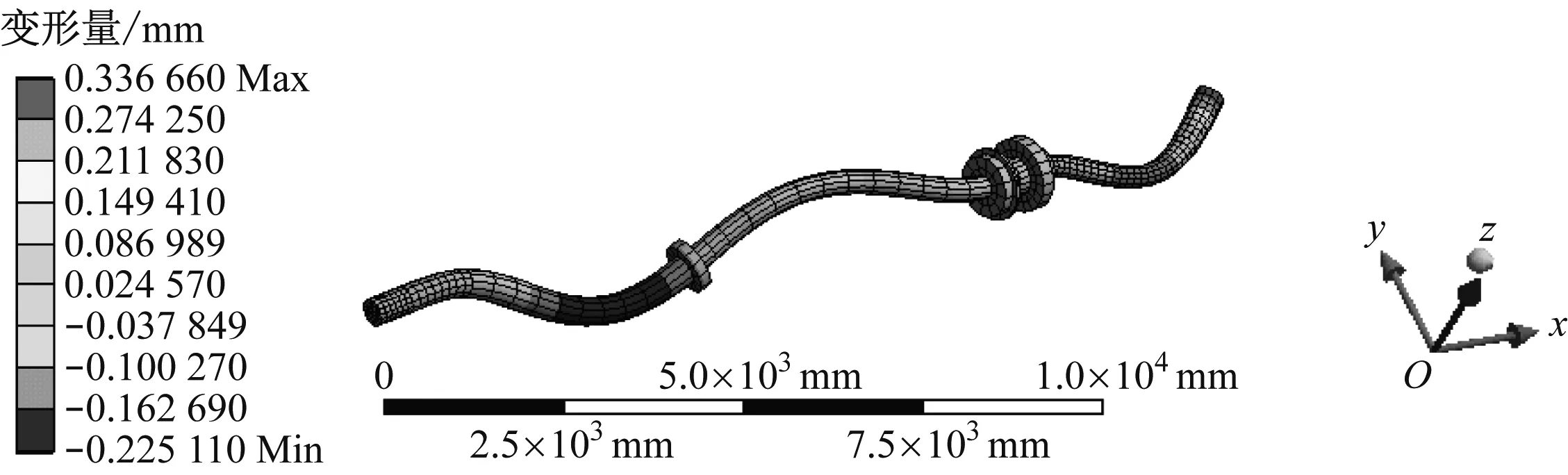
d) 10阶模态图5 船舶推进轴系横向分量振型

4.2.3 垂向分量振型

提取船舶推进轴系总体振型的垂向分量，得到各阶模态的垂向分量振型见图6。由图6可知：4阶模态的垂向变形量范围为-0.096 651～0.240 700 mm，最大垂向变形量出现在轴系尾部；5阶模态的垂向变形量范围为-0.561 030～0.560 990 mm，最大垂向变形量出现在中间轴与曲轴连接位置；8阶模态的垂向变形量范围为-0.026 571～0.406 680 mm，最大垂向变形量出现在中间轴中段位置；10阶模态的垂向变形量范围为-0.328 220～0.174 500 mm，最大垂向变形量出现在轴系前端位置。通过比较可得：正向4个阶次模态的垂向分量均相对较大，5阶模态的横向变形分量最大。

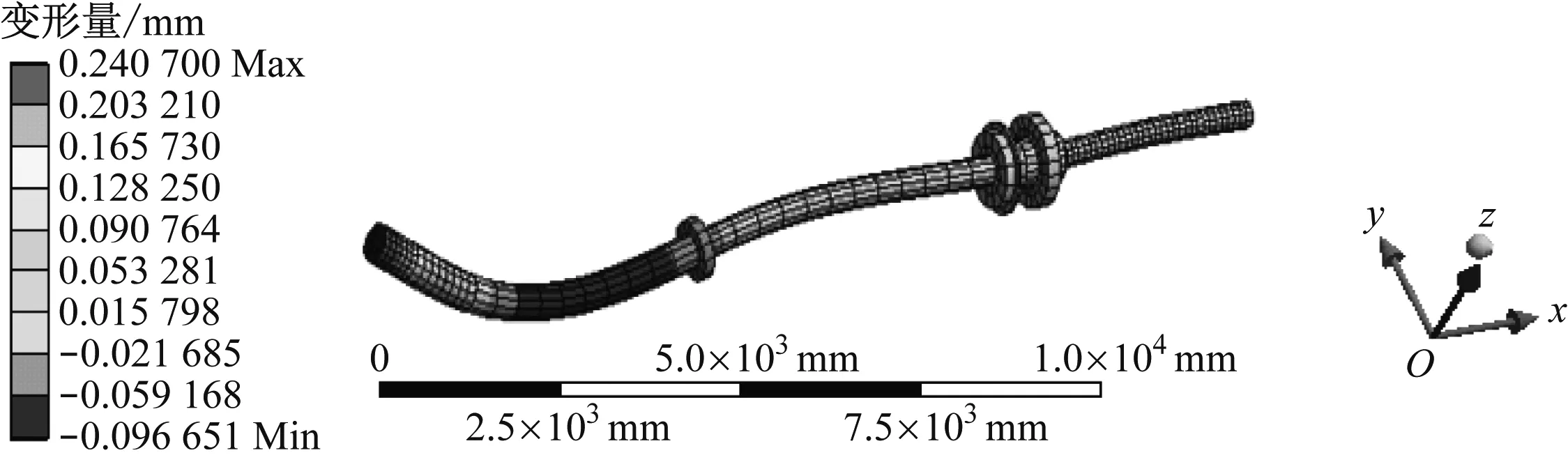
a) 4阶模态

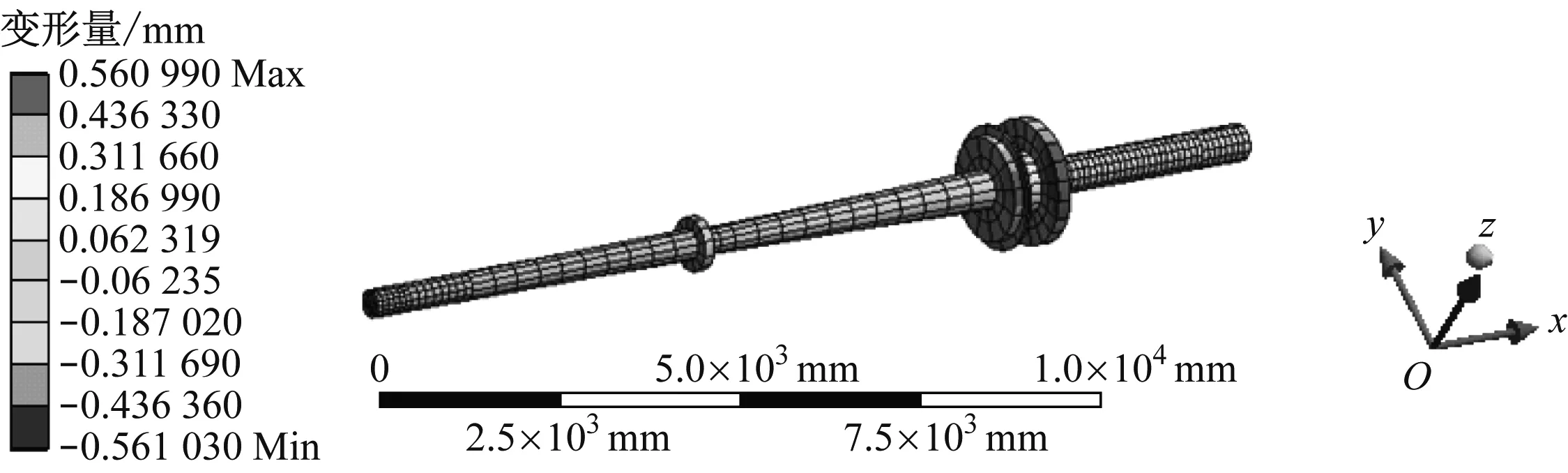
b) 5阶模态

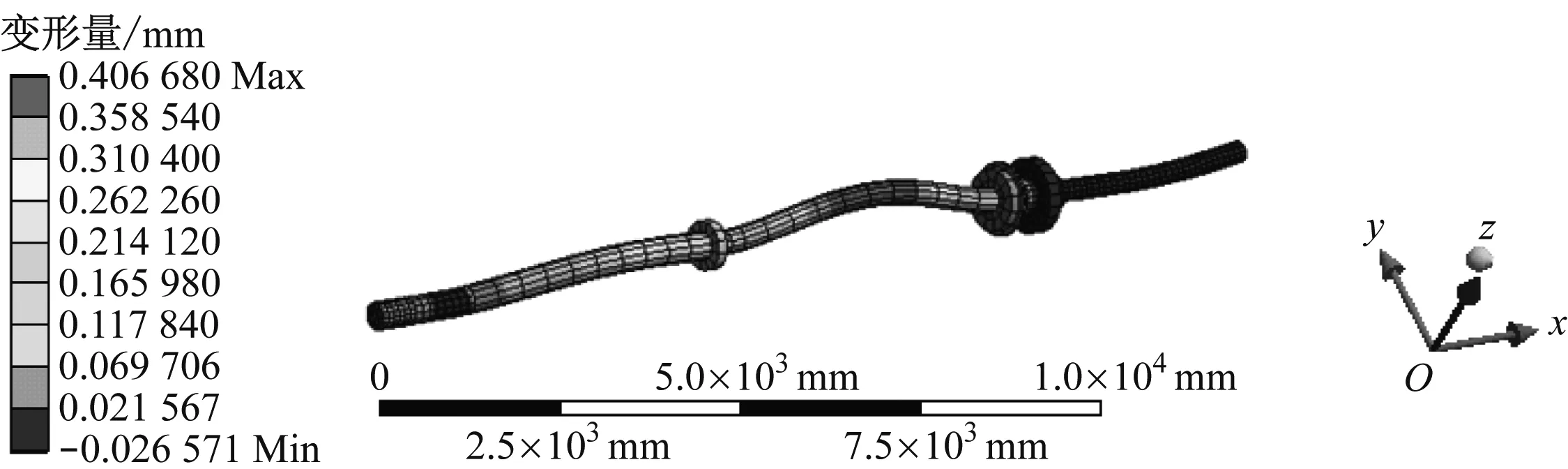
c) 8阶模态

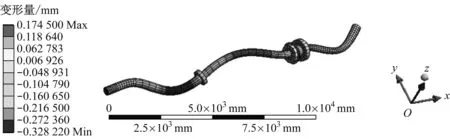
d) 10阶模态图6 船舶推进轴系垂向分量振型

5 试验验证

根据仿真对象设计船舶轴系横振试验，试验海域为中国东海试航区，海况为3级，风力为蒲氏3级，海水温度为20 ℃，海水密度为1.020 t/m，水深约为60 m；船舶为压载工况，艏部、舯部和艉部吃水分别为4.3 m、6.0 m和7.7 m，实测转速范围为30～89 r/min。采用频谱变换与谐次分析方法对实测数据进行处理，得到不同谐次轴系的横振频率和振幅等特征值。将仿真结果与试验数据相对比，结果见图7。由图7可知：有2个实测横向共振频率与4阶模态振动频率吻合，船舶推进轴系模态计算结果与实船试验结果的一致性较好。

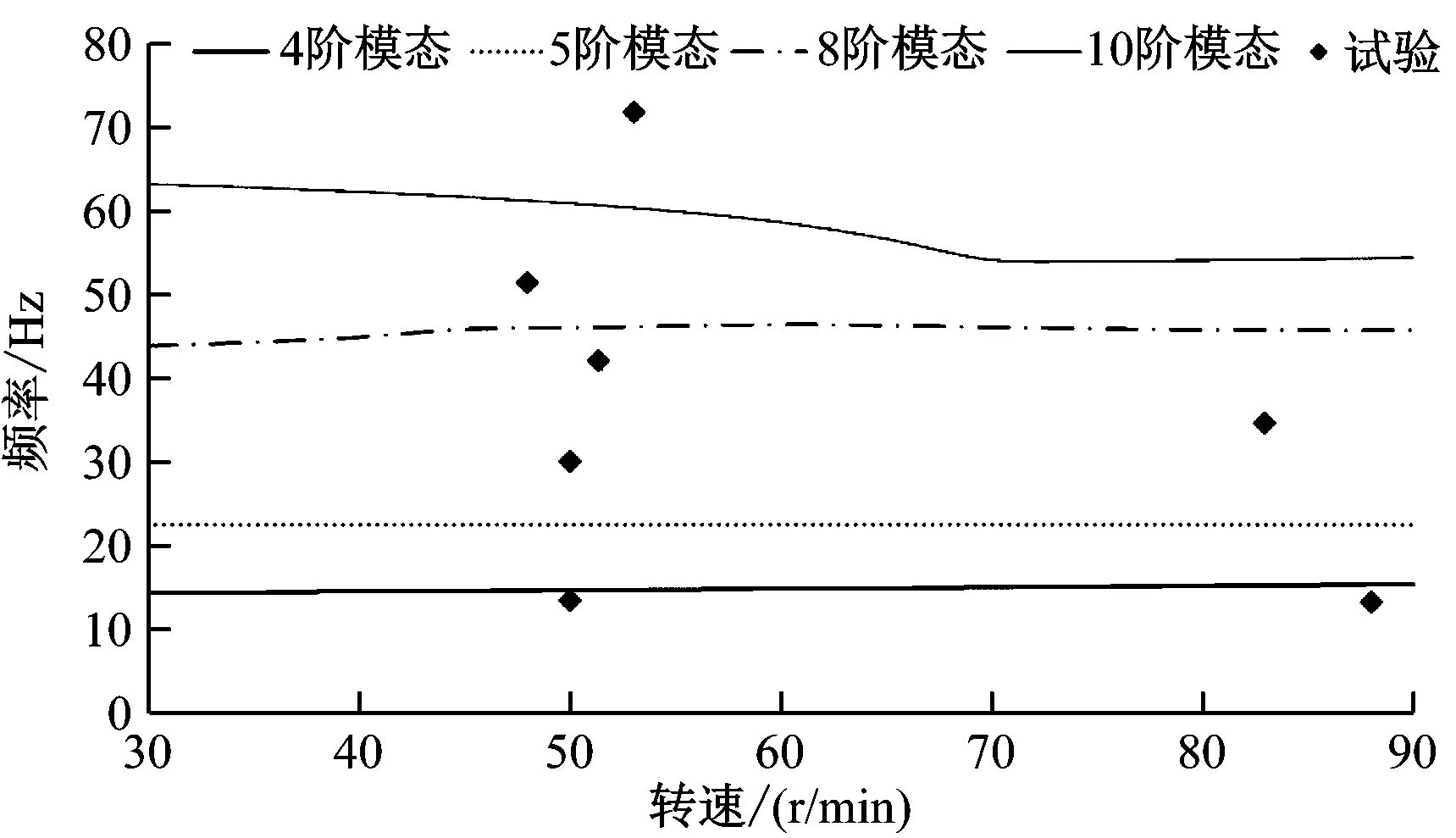
图7 仿真结果与试验结果对比

6 结 语

采用有限元理论形成的可变油膜刚度系数船舶推进轴系模态仿真方法，可更精确地对船舶推进轴系的模态特征量进行计算分析，得到船舶推进轴系模态特征与轴转速之间的关系。将船舶推进轴系模态仿真结果与实船试验数据相对比，结果表明，模态计算结果与实船试验结果的一致性较好，验证了本文提出的方法的准确性，该方法可为船舶推进轴系振动设计和校核提供理论支撑。