渤海简易独腿导管架节点全周期疲劳分析

杨 俊， 张延辉， 何 力， 王逢军

(海洋石油工程股份有限公司，天津 300451)

0 引 言

海洋平台在海上运行期间会受到风、浪、流和冰等多种环境荷载的作用。由于风和流的作用频率与海洋平台的自振频率差异较大，对导管架节点的整体疲劳影响很小，目前国内外相关规范对海洋平台进行的疲劳分析主要集中在波浪疲劳方面。由于不同海域的冰参数差异明显，各规范在海洋平台的冰力计算和冰条件取值方面尚未形成统一的方法。

针对冰激振动和疲劳研究：季顺迎等和兰志刚等基于辽东湾定点多年的冰情观测资料研究了冰激振动监测和海冰参数；岳前进等研究了柔性结构物在不同冰速下的破坏情况和荷载模式，提出了准静态振动、稳态振动和随机振动，同时对稳态振动情况下出现的频率锁定情况进行了观测和分析；张大勇等分析了冰与直立腿抗冰结构相互作用的过程，提出了冰激直立腿平台的疲劳寿命分析流程。上述研究很少对独腿简易平台在不同冰激模式下的振动疲劳进行研究；同时，对平台在服役全周期内受到的冰激振动与波浪疲劳的累加损伤影响开展的研究也较少。

考虑到独腿平台具有对称分布的结构特点，采用SACS软件对其进行简易疲劳分析，筛选出重点关注的节点和影响最大的荷载的方向。在此基础上，针对平台在不同冰速下受到的稳态振动和随机振动影响，分别采用ANSYS软件的瞬态分析和谱分析方法得出关注节点的冰激振动疲劳损伤；针对非冰期的情况，采用SACS软件进行详细的波浪谱疲劳分析，得出关注节点的波浪疲劳损伤，并采用Palmgern-Miner线性累积损伤理论对冰激振动疲劳和波浪疲劳进行叠加处理，完成全周期的疲劳分析。

1 计算方法

1.1 Palmgern-Miner线性累积损伤理论

Palmgern-Miner线性累积损伤理论假定：在给定的应力水平下，累积损伤的速度与之前的载荷历程无关，且加载顺序不影响疲劳寿命的计算值。一定时间内多个工况的累积损伤

D

的表达式为

(1)

式(1)中:

S

为疲劳强度安全系数，

S

>1；

n

为第

i

种工况的应力循环次数；

N

为第

i

种工况的应力范围对应的许可应力循环次数，由S-N曲线确定。S-N曲线一般采用文献[1]中的WJT曲线。在WJT曲线计算无法满足疲劳寿命要求的情况下，需根据WJ1曲线的应用条件对节点焊趾进行打磨处理，经过处理的节点的疲劳寿命能比处理前增加1倍。

1.2 波浪简化疲劳

简化疲劳评估方法是一种间接的疲劳评估方法，又称许用应力范围法，通过对作用的应力范围

S

与许用值

S

进行比较确定疲劳强度。

U

=

S

/S

(2)

式(2)中：

U

为应力范围与许用值的比值，

U

<1表示疲劳满足要求。

通过简化疲劳分析，可筛选出导管架结构上疲劳影响较大的节点和对应的荷载方向。

1.3 波浪谱疲劳

波浪谱分析理论在国内外相关规范和相关研究中均有详细的描述，可采用SACS软件完成相关分析，流程见图1。

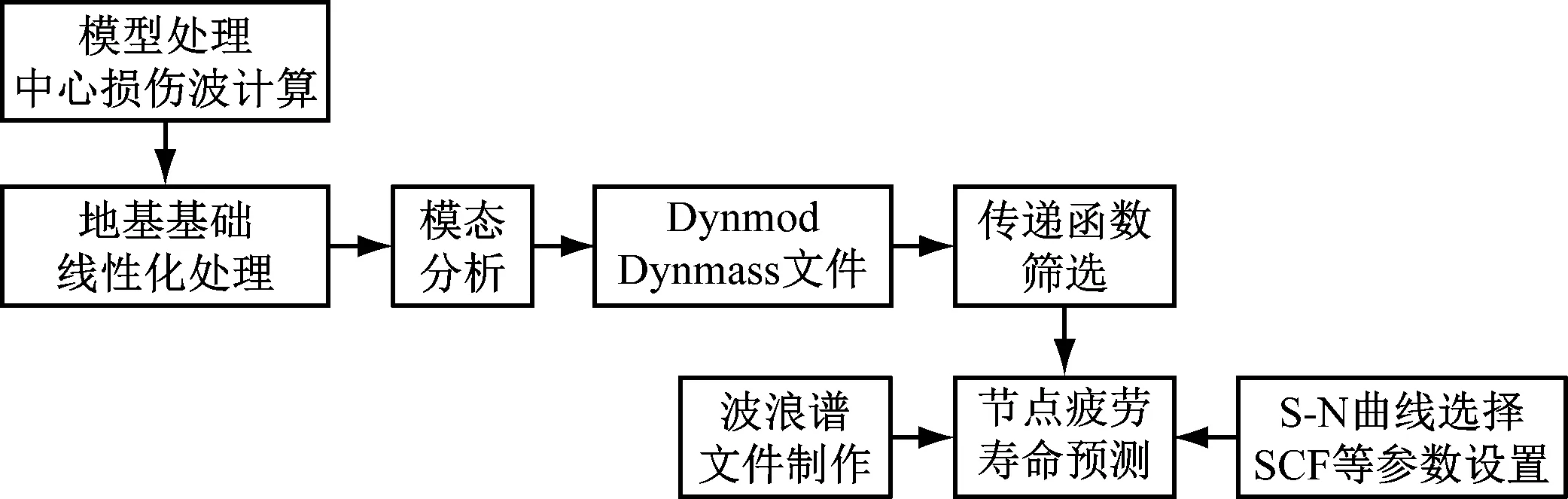
图1 基于SACS软件的波浪谱疲劳计算流程

1.4 冰激振动疲劳

根据岳前进等基于现场测量进行的观测和理论研究，根据冰速的不同，冰对结构物的振动激励主要分成3种：当

v

<2 cm/s时，冰激振动为稳态振动；当

v

=2～4 cm/s时，冰激振动为稳态振动；当

v

>4 cm/s时，冰激振动为随机振动。在进行疲劳计算时，需考虑稳态振动和随机振动的影响。

1.4.1 稳态振动冰荷载

结构物在稳态振动模式下的冰荷载时程曲线见图2，其中：

T

为结构物一阶固有频率

f

对应的周期;

F

为结构冰荷载的最大值，近似取静冰荷载计算。

F

=

mIf

σ

Dh

(3)

图2 结构物在稳态振动模式下的冰荷载时程曲线

式(3)中：

m

为形状系数，对圆形截面取0.9；

I

和

f

分别为嵌入系数和接触系数，当

D

≥2.5 m时，

If

=0.4；

σ

为冰无侧限压缩强度，渤海区域一般取

σ

=2.0 MPa；

D

为冰挤压结构的宽度，m；

h

为冰厚，m。Δ

F

=

qF

(4)

式(4)中：Δ

F

为最大冰荷载与最小冰荷载之差，kN；

q

为系数,与冰速相关，本文取

q

=0.5。根据不同冰况下的冰荷载时程曲线，通过ANSYS的时域分析可得到关注节点处的应力幅值，各应力幅值的循环次数

n

的表达式为

n

=

P

×

d

×24×3 600×

f

(5)

式(5)中：

d

为冰期，渤海区域按45 d考虑；

P

为

j

工况出现的概率，可通过冰厚概率密度函数

f

(

h

)和冰速概率密度函数

f

(

v

)拟合;

f

为结构的自振频率。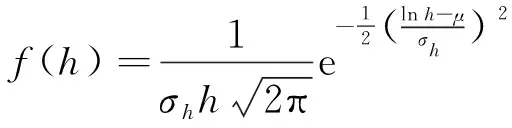

(6)

(7)

式(6)和式(7)中：

σ

为冰厚概率均值；

μ

为概率方差;

σ

为冰速概率均值。1

.

4

.

2 随机振动冰荷载

(8)

(9)

通过ANSYS对上述各工况下的冰载荷谱进行分析，可得出节点处的应力方差。若假设节点处的应力峰值符合瑞利分布，则结构物的应力峰值概率密度函数

p

(

σ

)的表达式为

(10)

式(10)中：

σ

为结构应力峰值，MPa；

σ

为应力标准差，MPa。每种冰况在1 a内的循环次数

n

可根据式(5)统计，同时对应力分布进行积分，可得到

j

工况下第

i

个变幅应力Δ

σ

的循环次数

n

的表达式为

n

=

n

×

P

(Δ

σ

)

(11)

式(11)中：

P

(Δ

σ

)为第

i

个变幅应力出现的概率。

2 模型及主要尺寸参数

本文以渤海辽东湾北部某简易不加抗冰锥独腿三桩导管架平台(以下简称C平台)为研究对象，其设计使用寿命为17 a。C平台上部主甲板的尺寸为14 m×14 m，操作质量为620 t，标高为EL.(+)14.3 m；下部为间距为20 m的3个桩，桩径为1.1 m，下部结构总质量为450 t，水深为16.6 m；主腿尺寸在有斜撑处为∅4 000 mm×65 mm，在其余部位为∅4 000 mm×38 mm。

C平台的SACS和ANSYS计算模型见图3，其中：SACS计算模型用于进行波浪简化疲劳和波浪谱疲劳计算，模型中标注了各类型节点的区域；ANSYS计算模型采用板壳单元和质量点单元建模，用于进行冰激振动的时域和谱分析，ANSYS网格划分中在关注节点位置进行了加密;A、B、C、D和E为节点位置区域。为简化计算，边界为考虑5倍桩径处固定约束。波浪荷和冰载数作用位置标高为EL.(+)3.2 m。

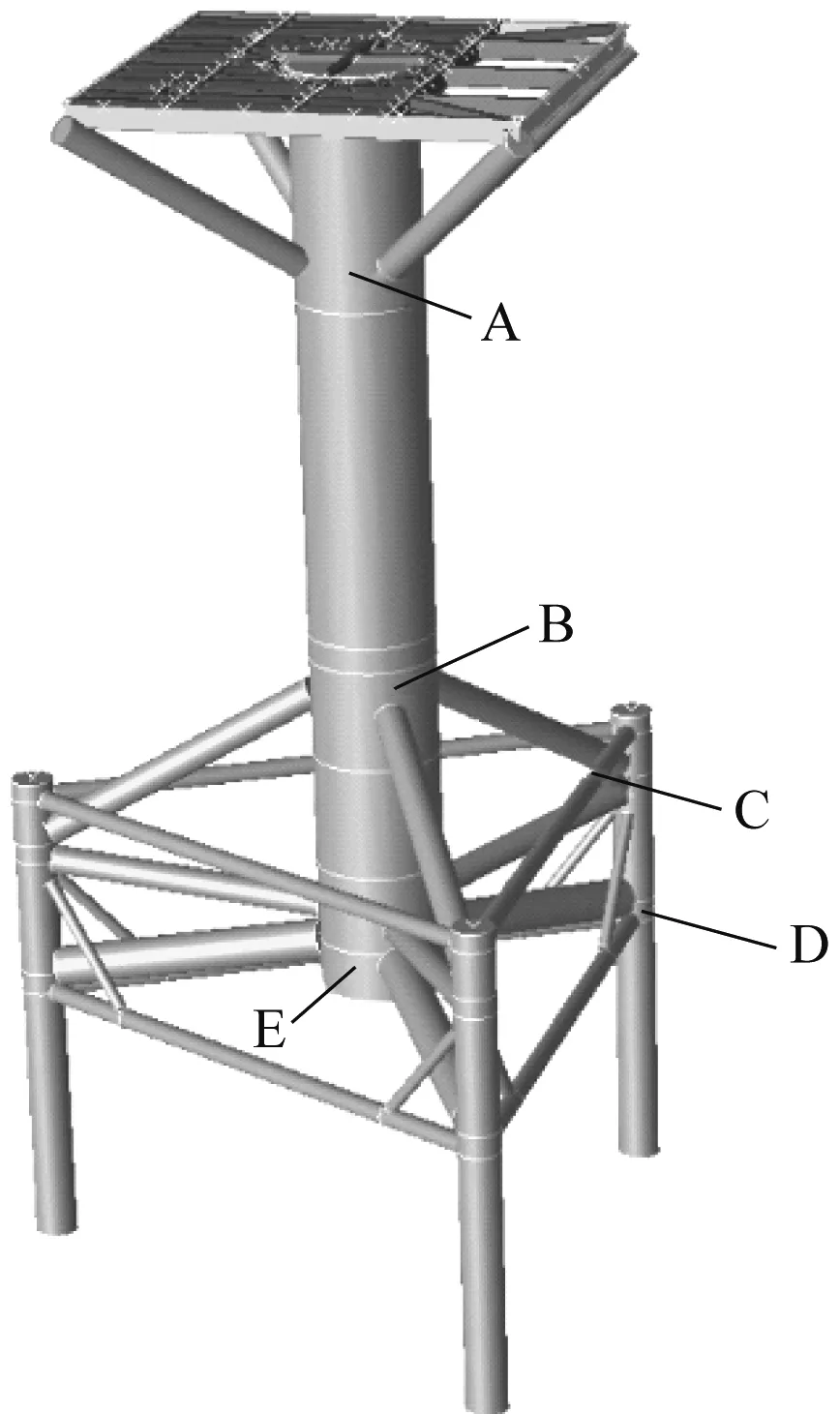
a) SACS计算模型

b) ANSYS计算模型图3 C平台的SACS和ANSYS计算模型

3 计算结果及分析

3.1 波浪简化疲劳计算

通过简化疲劳分析，得到SACS计算模型主要节点的简化疲劳

U

值见表1。

表1 SACS计算模型主要节点的简化疲劳UC值

通过计算发现，B区域LG03节点的疲劳受波浪的影响最大，进一步分析该节点在0°～120°波浪角度下的疲劳

U

值，结果见图4。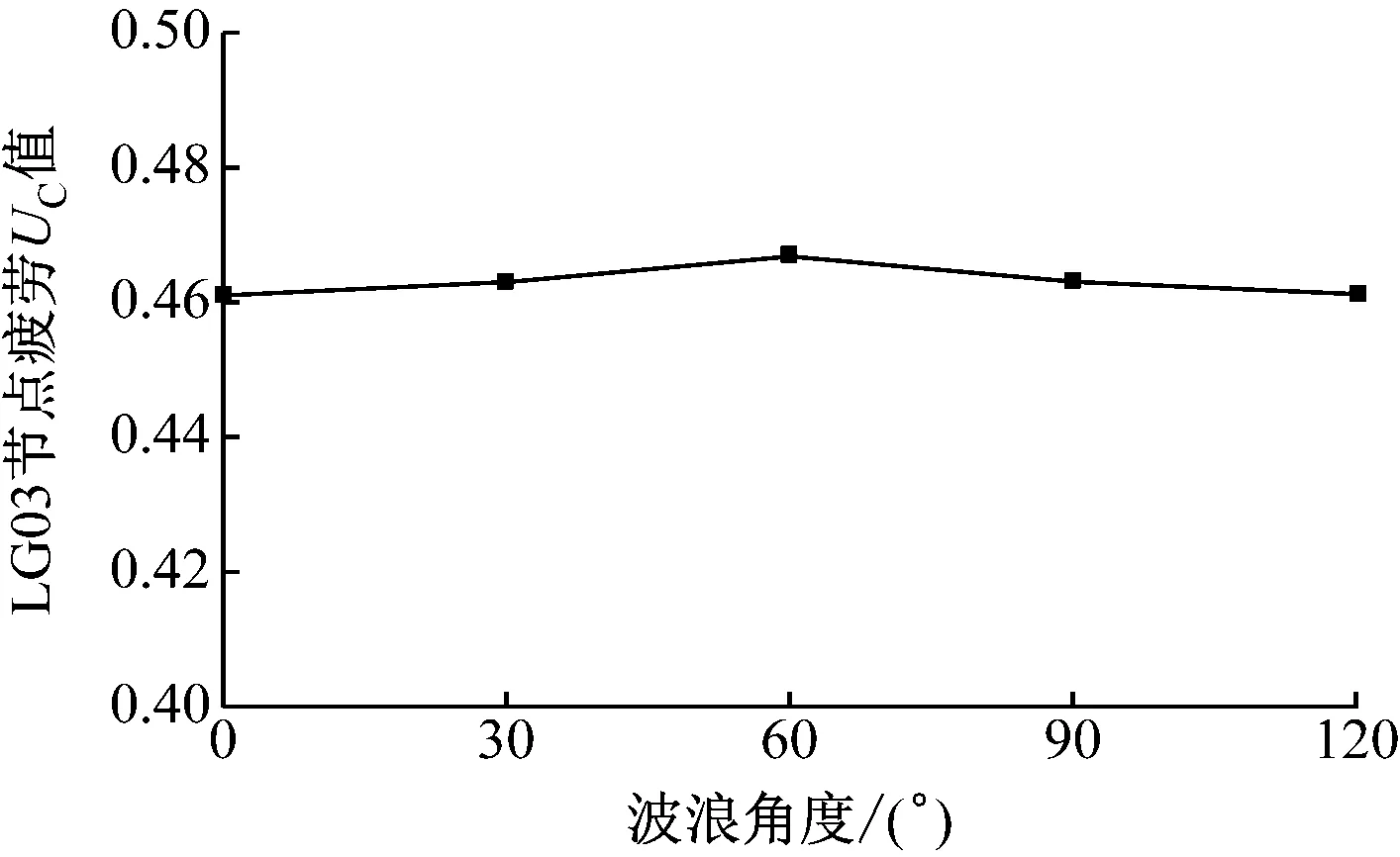

图4 LG03节点疲劳UC值随波浪角度的变化情况

由图4可知，由于C平台的结构具有对称性，波浪入射角对节点疲劳的影响较小。本文主要对LG03节点在波浪角度为60°时的波浪谱疲劳和冰激振动疲劳进行分析。

3.2 波浪谱疲劳分析

通过SACS计算C平台的固有频率，结果见表2，波浪角度为60°时的基底弯矩传递函数见图5。

表2 通过SACS计算得到的C平台固有频率

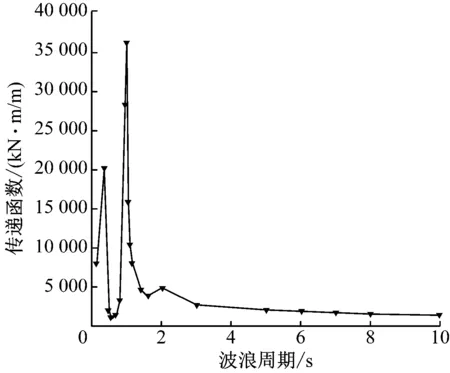
图5 波浪角度为60°时C平台的基底弯矩传递函数

根据API-WJT疲劳曲线，在不考虑安全系数的情况下，LG03节点的最短使用寿命为152.7 a，按平均有效冰期为45 d考虑，折算波浪荷载下LG03节点每年的疲劳损伤

D

为

(12)

3.3 冰激振动疲劳计算

根据式(6)和式(7)，采用文献[11]中的冰参数取值方式，将冰厚分为0～<9 cm、9～<18 cm、18～<27 cm和27～36 cm等4个区间；考虑到稳态振动与随机振动的区别，将冰速分为2～<4 cm/s、4～<20 cm/s、20～<40 cm/s、40～<60 cm/s和60～80 cm/s等5个区间。各种状况下冰厚与冰速的联合分布概率见表3。采用ANSYS计算模型的一阶模态周期为1.25 s。

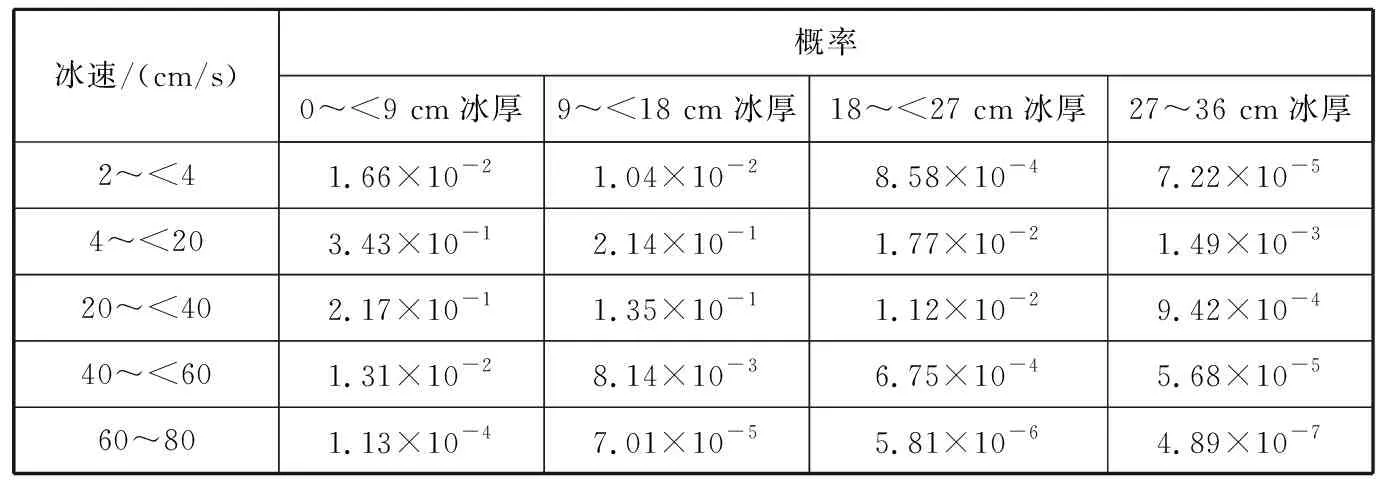
表3 各种冰况下冰厚与冰速的联合分布概率

1) 针对冰速为2～<4 cm/s的稳态冰振，每年各冰厚区间内的最大冰荷载

F

、平均应力幅范围和各工况下的疲劳损伤等见表4，典型冰荷载加载曲线和节点应力情况见图6～图8。

表4 稳态冰振情况下疲劳情况

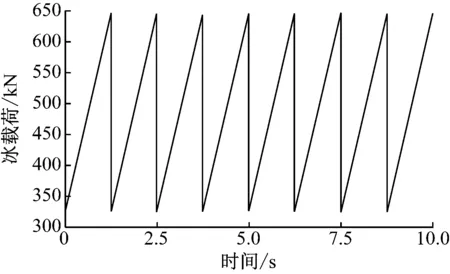
图6 冰荷载施加曲线

图7 节点处应力变化情况

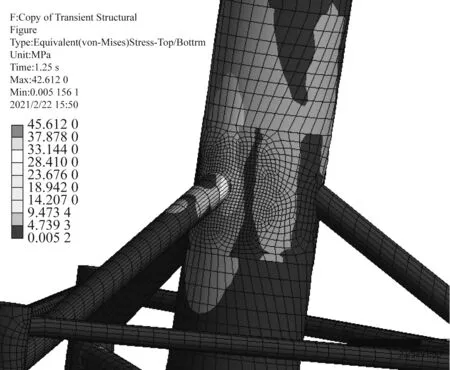
图8 节点应力分布情况

结合式(5)计算稳态冰振各冰厚区间下LG03节点每年的疲劳损伤

D

为

D

=∑

D

2·0

.

004 6

(13)

2) 针对冰速大于4 cm/s的随机振动，结合式(8)～式(11)，采用ANSYS进行应力谱分析，得到随机冰振情况下节点应力标准差见表5，节点疲劳损伤见表6。

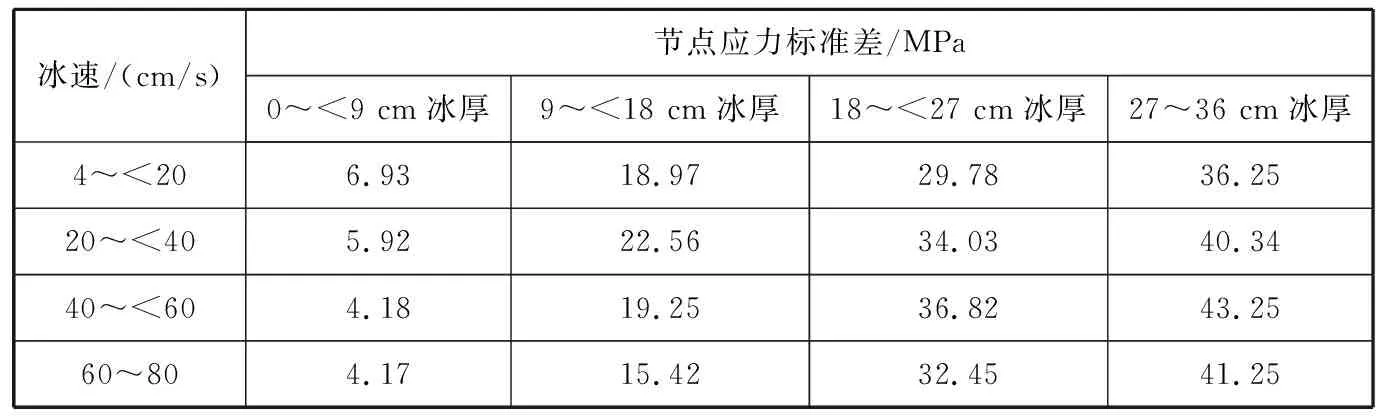
表5 随机冰振情况下节点应力标准差

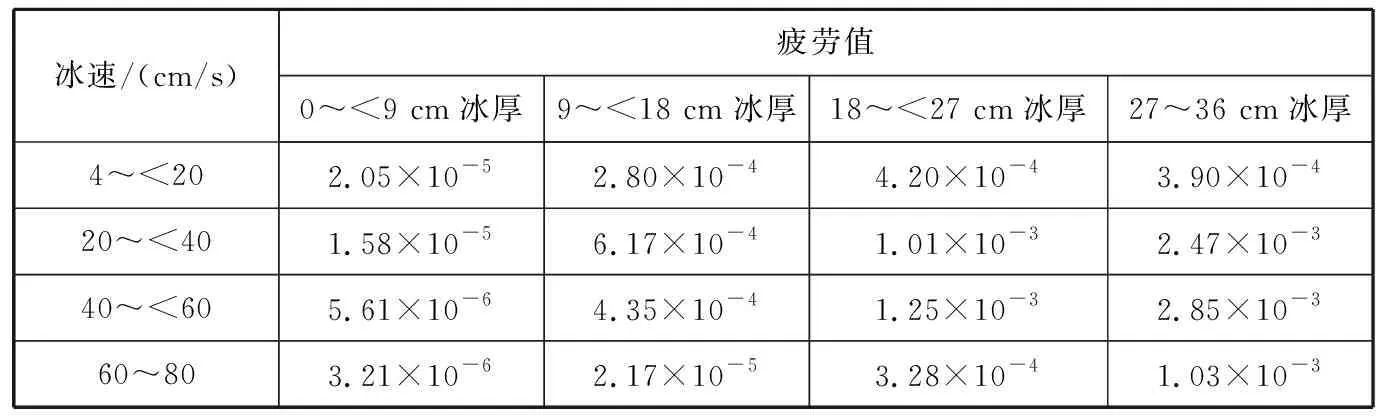
表6 随机冰振情况下节点疲劳损伤

结合式(5)计算各随机冰振工况下LG03节点每年的疲劳损伤

D

为

D

=∑

D

3·0

.

011 1

(14)

3.4 管节点疲劳损伤和疲劳寿命计算

仅考虑波浪的影响，C平台在WJT疲劳曲线下的疲劳寿命为175.4 a，满足设计年限的5倍安全系数下的85 a的要求。

在综合考虑波浪和冰激振动的影响的情况下，结合线性损伤原理对各工况下的疲劳损伤

D

进行叠加，节点疲劳损伤

D

=0.021 4 a，表明C平台在WJT疲劳曲线下的疲劳寿命为46.7 a，小于85 a，需按WJ1疲劳曲线使用要求对焊趾进行打磨处理，处理之后的疲劳寿命预计为93.4 a，满足疲劳寿命设计要求。

4 结 语

基于线性损伤理论，分别对各工况下的疲劳损伤进行分析和累加，可实现冰区导管架节点的冰激与波浪联合全周期疲劳分析。对于C平台，在综合考虑波浪和冰激振动的情况下，需按WJ1疲劳曲线使用条件对关注节点焊趾进行打磨处理，以满足疲劳寿命设计要求。

对比波浪与冰激振动疲劳的影响，有效冰期占全年的12.3%，疲劳影响达到73.4%。稳态冰激振动可激起管节点产生较大的疲劳应力幅值，虽然作用时间只占平台全周期的0.33%，但疲劳影响达到21.5%；虽然随机冰激振动激起的节点疲劳应力幅值小于稳态冰激振动，但其出现频率远大于稳态冰激振动，疲劳影响达到51.9%。在设计和使用冰区的简易平台过程中，需对冰激振动予以重视。同时，注意到目前国内外规范在冰荷载参数取值上差异较大，特别是对冰速、冰厚等参数的概率密度分布的研究较少，还需针对具体的使用海域进一步对冰况进行监测和试验研究。