一类偏微分方程初值问题的近似解析解法

王兵贤, 徐 梅, 张弘毅

(淮阴师范学院 数学与统计学院, 江苏 淮安 2233000)

0 引言

现代科学、技术、工程中的大量数学模型都可以用微分方程来描述,较多近代自然科学的基本方程本身就是微分方程.因此,科学和工程计算的一个主要任务也是求解微分方程的(特别是偏微分方程)定解问题.然而,由于较多背景意义下的偏微分方程,譬如流体力学问题往往不定常的、非线性的,加上黏性、湍流和激波等复杂的现象.因此,较多偏微分方程的解较难用解析形式来表示,从而也涌现出了较多有效的近似数值解法[1-6],包括有限差分方法、基本解方法、边界元、有限元方法以及同伦方法等等,但对于一些偏微分方程,特别是非线性发展方程,其收敛性和稳定性结果分析是近似数值解法研究中一个比较困难的.

基于此,本文研究如下偏微分方程初值问题:

utt=F(ut,u,ux,uxx,…)

(1)

u(x,0)=φ0(x),ut(x,0)=φ1(x)

(2)

如果F(ut,u,ux,uxx,…)=uxx,则方程(1)为典型的双曲型方程,如果F(ut,u,ux,uxx,…)=-ut+uxx+G(u),则方程(1)为典型的电报方程[7-8].而且,G(u)不同,所描述的物理背景也不同.本文考虑一种近似解析解法,该解法对于G(u)是非线性项时也是有效的.

1 近似解析方法

下面介绍近似解析方法的具体过程.首先,将方程(1)的两侧在0到t上积分,得到

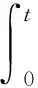
即

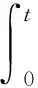
因此有

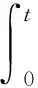
(3)

这里H[u]=F(ut,u,ux,uxx,…).

接着将方程(3)两侧再在0到t上积分,得

即

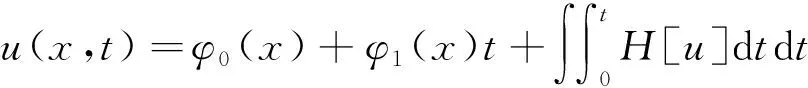
(4)

如果H[u]在t=0处的展开式为

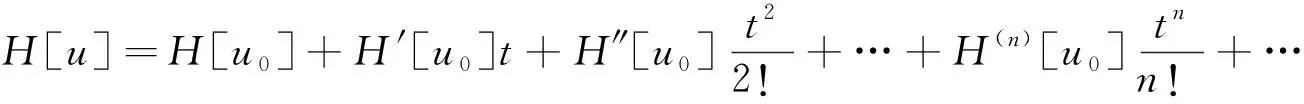
(5)

则将式(5)代入式(4)中得

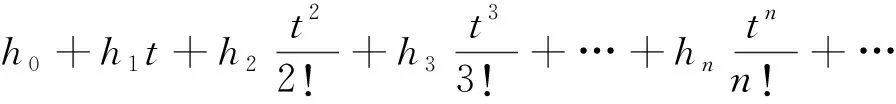
(6)

即

h0=φ0(x),h1=φ1(x),h2=H[u0],

h3=H′[u0],…,hn=H(n-2)[u0].

注1 式(6)实质上是u在t=0处的泰勒展开式,即

2 近似解析方法的应用

以3个问题为例,说明本文近似解析方法的有效性.

2.1 波动方程初值问题

考虑问题

(7)

式(7)是典型的波动方程初值问题,在数学物理方程中有经典的解析求解方法,运用本文讨论的方法,其基本解析过程如下:

在该问题中,根据方程(1)的形式,

H[u]=-uxx，

则

h0=sinx,h1=-sinx,h2=H[u0]=-uxx(x,0)=sinx,

h3=H′[u0]=-uxxt(x,0)=-(h1)xx=-sinx.

以此类推,计算得

即为方程解.

2.2 线性电报方程

考虑电报方程初值问题

其中

对于该问题,用本文讨论解析解法进行求解,过程如下:

h0=sinx,h1=0,

-ηh1-ζ2h0+(h0)xx+ζ2sinx=-ζ2sinx-sinx+ζ2sinx=-sinx,

-2ηh2-ζ2h1+(h1)xx-2ηcos0sinx+ζ2(-sin0)sinx=2ηsinx-2ηsinx=0,

-2ηh3-ζ2h2+(h2)xx-2ηsin0sinx+ζ2(-cos0)sinx=ζ2sinx+sinx-ζ2sinx=sinx.

以此类推计算得

即为方程的解.

2.3 非线性电报方程

考虑非线性电报方程初值问题

其中

则对于该问题,用本文近似解析解法进行求解过程如下:

h0=1-cosx,

h1=-(1-cosx),

-h1+(h0)xx-2sin(1-cosx)-cosx+2sin(1-cosx)=

1-cosx+cosx-2sin(1-cosx)-cosx+2sin(1-cosx)=1-cosx，

-h2+(h1)xx-2cos(h0)·h1+cosx-2(1-cosx)cos(1-cosx)=

-1+2cosx-cosx+2(1-cosx)cos(1-cosx)+cosx-2(1-cosx)cos(1-cosx)=

-1+cosx，

cosx-2(1-cosx)2sin(1-cosx)+2(1-cosx)cos(1-cosx)=

-h3+(h2)xx+2sin(h0)h1-2cos(h0)h2-cosx-2(1-cosx)2sin(1-cosx)+

2(1-cosx)cos(1-cosx)=1-cosx+cosx-2(1-cosx)sin(1-cosx)+

2(1-cosx)sin(1-cosx)-cosx-2(1-cosx)2sin(1-cosx)+2(1-cosx)cos(1-cosx)=

1-cosx.

以此类推计算得

即为方程的解.

3 总结

由于复杂工程背景的驱动,出现了大量非线性偏微分方程初值问题,本文所讨论的近似解析解法对于非线性偏微分方程初值问题同样适用.另外,较多偏微分方程反问题求解对于正问题的求解方法有较高的要求,非线性性的处理也面临着较大的困难.因此,本文所讨论的方法也可以用于反问题的求解中,拟另文讨论.