核心素养背景下小学生运算能力的培养策略
2021-10-01彭国庆
彭国庆


[摘 要]运算能力是数学核心素养之一,在小学数学教学中可以运用“多元表征以明运算之理、多类型练习以熟运算之术、融入问题解决以善运算之用、多内容关联以通运算之道”四个策略培养学生的运算能力。
[关键词]运算能力;培养策略;核心素养
运算是小学数学教学中最传统的内容之一,运算能力自然也备受重视,成为大家关注的基础学习能力之一。《义务教育数学课程标准(2011年版)》将运算能力确定为十大数学核心概念之一,关于运算能力的描述是“运算能力主要是指能够根据法则和运算律正确地进行运算的能力” 。下面笔者就结合自己的教学实践从“明理、熟术、善用、通道”这四个方面谈小学生运算能力的培养策略。
一、多元表征以明运算之理
数学学习不仅要关注学习的结果,更要关注学习的过程。教师在教学中经常遇到这样的情况:学生在家长或非专业人员的提前教学下已经学习了两位数乘两位数的计算方法,但他们对算理却理解甚少,如学生在计算36×12时,能够记住36×12的竖式书写程序,但是对于2乘36、1乘36的结果分别表示什么,乘积又表示什么,却说不出来。对算法理解的多少不仅会对后续的运算学习有影响,还影响着问题解决的能力,所以计算教学不仅要教学生知道怎么算,还要结合具体内容采用多元表征方式帮助学生理解算理。
1.创设情境,理解算理
数学运算本身是抽象的,因此学生会感觉计算是枯燥的,理解算理更是犹如在枯燥的程序中寻找枯燥的理由。然而,合适的情境可以破除“枯燥”并帮助学生在有意义的、有趣的情境中理解算理。如计算36×12,教材呈现了这样的数学情境图(如图1):
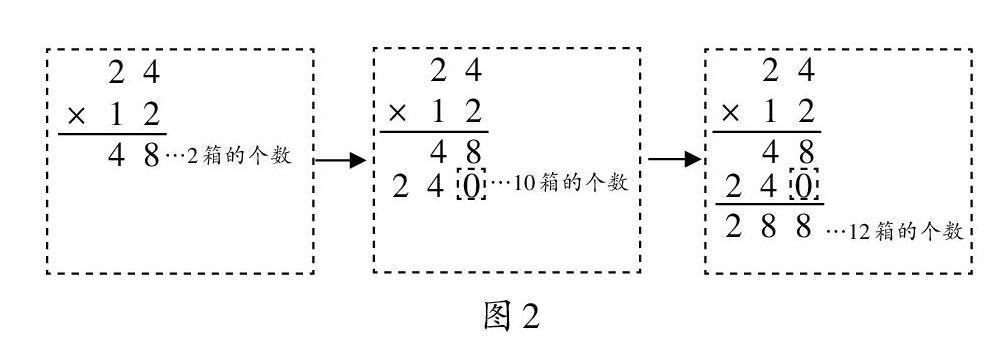
要计算12箱南瓜有多少个,可以分两步:先算2箱有多少个南瓜,算式是2×24=48(个);再算10箱有多少个,算式是10×24=240(个);然后把两次计算的总数相加,得到48+240=288(个)。这样就是把12箱南瓜的个数进行分拆计算,而这样的分拆计算,正好可以帮助学生理解24×12的竖式计算过程(如图2)。
至此,教师再针对竖式中的每一步进行提问,帮助学生理解每一步运算的含义以及最后结果的含义,进而达到知其然知其所以然的学习目的。
再如,教学混合运算时,创设问题情境可以有效帮助学生理解混合运算的顺序。如1副羽毛球拍是70元,1个羽毛球是4元,买2个羽毛球和1副羽毛球拍一共要多少元?要解决这个问题就要先算出2个羽毛球一共要多少元,算式是2×4,然后再加上1副羽毛球拍的钱数,写成综合算式是70+2×4。把分步计算的过程对应到递等式过程中来,学生就能够理解乘法和加法的混合运算中为什么要先算乘法了。
2.动手操作,理解算理
动手操作是学生学习数学的有效学习方式。在计算教学过程中,动手操作可以帮助学生把抽象的数理应用过程变为具象化的可视化操作活动,使学生在可视化的操作活动中充分理解算理,掌握算法。如教學用凑十法计算9加几的加法计算时,教师先出示一个和例题同样的情境图,即“一个盒子里装有9个苹果,盒子外面有4个梨”(有经验的教师都是用可移动的板贴图来表示),然后提出问题“一共有多少个水果?”。学生可以将1个梨“放”进装有苹果的盒子里,凑满10个,然后再加上盒子外面的3个梨,这样得出一共有13个水果。最后让学生完成“试一试”(如图3)。
学生在移一移、圈一圈的操作活动中,理解了用凑十法计算9加几的方法的分解过程,体会到凑十法计算的快捷性,还为后面继续学习8、7、6等加几做好了铺垫。
3.几何直观,理解算理
数是抽象的,形是具象的,在运算的过程中可以通过几何直观帮助学生理解算理。如对于同分数加减法,教材呈现了这样的几何直观图(如图4):
又如,在计算分数乘分数的时候,教材呈现了将长方形面积等分和再等分图(如图5)帮助学生理解分数乘分数的算理。
两次等分图既展现了计算的过程,同时又包含计算的结果,可以说是几何直观中的经典之作。通过这样的直观图就能帮助学生理解分数乘分数就是分了再分、取了再取的道理。
二、多类型练习以熟运算之术
对学生运算能力的培养还需使学生能够熟练应用运算方法进行快速、正确的运算,具体体现在加强对学生口算、估算、笔算(竖式计算、递等式计算)能力的培养。
1.加强口算练习
口算是所有运算的基础,加强口算练习,就相当于做好运算学习的塔基工程。口算练习要从一年级抓起,从10以内的加减法开始逐步拓展到多位数的口算,逐步加深口算的难度;从整数的口算到小数、分数、百分数的口算,从数的口算到式的口算,逐步拓展数与代数的运算领域,从而拓展口算练习的宽度和高度。 要加强口算练习就要天天练,练习的内容主要以与即将学习的新知有关的旧知(运算)以及学生易错的口算题为主,每天练习的量为10题左右,保证学生能在加强基础口算的同时,纠正一些常见的口算错误。口算的形式可以题组对比的方式,例如在两位数乘两位数的口算中设置对比题25×4和24×5,可帮助学生区分算式不同的同时培养学生认真审题的习惯。
2.加强估算练习
估算是学生进行运算以及检验运算结果的方式之一,但学生的估算正确率远远低于口算和笔算的正确率,一方面是估算的应用频率较低,另一方面是学生的估算意识没有初步形成。这样就造成了学生在解决实际问题时估算能力不足,教师亟须把现实生活中应用广泛的估算与数学中的估算学习对应起来。加强估算,首先要掌握估算的方法。在学生刚认数时,经常给出“17和12这两个数,哪个数最接近20?哪个数最接近10?”这样的练习,就是在为后面学生学习估算做好准备,而后让学生在具体的问题情境中认识到估算的必要性,理解估算的方法。如创设问题情境:张大叔把收获的生姜装在同样大的袋子里, 一共装了 40袋, 他称了其中的 4 袋, 结果分别是 18 千克、 21 千克、19 千克、 23 千克。 他一共收获生姜大约多少千克?学生体会到这些数都是接近20的,虽然有的数是超过20的,有的数是不足20 的,但是只要接近20都可以将其看成20后进行估算。通过解决问题,学生就能掌握估算的方法,体会估算的实际应用价值。
3.加强笔算练习
小学的笔算主要有两种形式,一是四则运算,主要是列竖式进行运算,二是四则混合运算,主要是采用递等式的方式进行运算,前者是后者的基础,后者是前者的延续和再使用。笔算练习应该从低年级的加、减法和乘、除法开始,首先夯实进位加法和退位减法的基础;其次夯实连续进位和连续退位的减法的基础,这些都是学生的易错点;再次夯实两位数乘一位数的乘法和除法运算的基础,在夯实运算的过程中加强算法的指导,如在乘法中重点指导学生掌握进位书写以及乘积加进位数的方法,除此之外,还要帮助学生区分两位数乘两位数的两次乘积的乘法运算和最后的加法运算,减少学生混淆这两种运算的问题。四则混合运算是学生进行数运算的终极目标,学生在计算时不仅要熟练解决运算顺序的问题,同时还要保证每一步计算结果的正确性,因此,混合运算的练习要本着由易到难的原则,在激发学生获得成功感的同时提高学生的运算能力。在笔算练习中还要加强简算练习,因为除了按照一定的规则、顺序进行运算,简算能运用运算规律或性质使得原本复杂的运算变得简单和快捷。因而,加强简算练习,除了能提高学生的运算能力,還可以培养学生的观察能力、辨析能力和灵活应用知识的能力,培养学生思维的灵活性和深刻性。
三、融入问题解决以善运算之用
当下的运算学习多是融合在问题解决中,通过运算解决一些实际问题,增强学生的运算能力,因此在解决问题中还要强化学生善于运用合理简洁的运算途径去解决实际问题的能力。
1.善于运用估算解决实际问题
学生在日常生活中常常要解决一些关于预算的问题,如购买高铁票:商务座2114元/张,一等座1095元/张,二等座689元/张,只买一种票,买3张要准备多少元?这个问题可以用笔算解决,也可以用估算解决,但是把每种票价都多看一点,看成整千整百数后进行估算,就很容易得出预算结果,如商务座看成2200元/张,3张大约需要2200×3=6600(元);一等座看成1100元/张,3张大约需要1100×3=3300(元);二等座看成700元/张,3张大约需要700×3=2100(元)。这就体现了课程标准中指出的“用合理简洁的运算途径去解决实际问题”。除了数与代数领域,估算在统计与概率领域中的应用也是比较频繁的,如根据折线统计图中给出的数据预测即将出现的数据;图形与几何领域中结合方格图估计一个不规则图形的面积;根据一个圆柱形玻璃瓶中水的体积,估测和它同样的2个瓶子中的水的体积;等等。在诸多的问题解决中体会估算在问题解决中的便捷性,能增强学生估算的应用意识和使用频率。
2.善于运用简便运算解决实际问题
数学本身就是追求简洁的,教师在教学问题解决策略时要善于选择并运用简便运算体现数学的简洁性,以增强学生的运算能力。如计算长方形的周长时选用“周长=(长+宽)×2”进行计算,计算长方体的表面积时选用“S=2(ab+ac+bc)”进行计算,就比较简便。一个问题可以用加法或者乘法计算解决时优选乘法计算,同理,一个问题可以用减法或者除法计算解决时优选除法计算。如解决“张晓华和赵丽同时从同一地点出发,张晓华向东走,每分钟走60米;赵丽向西走,每分钟走55米。经过6分钟他们相距多少米?”这样的问题时,教师就要引导学生选用“(60+55)×6”进行列式计算,尽可能使得运算简便。当然,这种简便运算的选择是在对比的前提下产生的,所以教师在教学过程中要注意结合实际问题引导学生进行比较,在多样化算法的基础上实现算法的优化。
四、多内容关联以通运算之道
所谓运算之道就是运算中蕴含的基本规律、基本性质等。学生学习运算,不仅要知道现阶段所学运算的方法和算理,还要能够善于发现、总结运算中的规律,善于将现阶段所学的运算知识融入整个运算知识体系中去,以通晓运算之道。
1.疏通联系,理解运算原理的一致性
数的运算犹如一颗石子投入水中,激起的涟漪不断由内向外晕开形成的同心圆,这些同心圆是以运算的基本规则为圆心,不同类型的数为半径的。教师在带领学生学习运算的时候,要不断地帮助学生梳理、分析现有知识与已有知识之间的联系,找到它们的共性之处,使学生形成完整的认知结构。如对于加、减法计算都是基于相同计数单位上的数才能够相加、减这一知识点,教师要帮助学生梳理为什么要小数点对齐;在教学异分母分数加、减法的时候,教师要引导学生明白通分成同分母分数进行加减运算的道理,然后把整数、小数、分数的加减运算方法进行梳理和对比,帮助学生找到运算方法的一致性,形成完整认知结构。再如两位数乘两位数的笔算过程中蕴含了乘法的分配律,所以教学乘法分配律时,教师要引导学生回头看两位数乘两位数的运算过程,合理解释这一运算律在乘法竖式运算中的应用,促进学生理解竖式和递等式运算的内在原理的一致性。
2.勾连关系,理解运算规律和方法的一致性
数学知识之间是有内在的规律和方法一致性的。如教学整数除法时,教师要引导学生发现除法的规律,如被除数一定,除数越大,商越小。在整数、小数、分数的学习中不断推广这些规律后,学生就能体会到运算规律的一致性。又如学习了除法、分数、比之间的关系后,学生在学习分数基本性质时,就可以结合商不变性质解释分数的基本性质,在学习比的基本性质时,就可以结合分数基本性质解释比的基本性质……这样的互释使看似不同性质的规律通过内在的联系呈现了一致性。再如乘法和除法存在互逆关系,教学分数除法的时候,借助倒数把分数除法转化为分数乘法,就能使学生体会到两种算法之间的一致性。这样勾连运算之间的关系,能有效地把运算知识串联起来,帮助学生构建新知识网络。
3.关联迁移,理解运算蕴含数学思想方法的一致性
数学运算能力还是多因素融合的能力,包含理解、运用数学思想方法。如在归纳总结加法交换律时,要求学生根据问题情境写出几个等式,经过观察后发现规律,将这种合情推理的方法迁移到后续的加法和乘法运算律的学习中,所以在这些规律的总结方面要能够体现数学思想方法的一致性。又如探究小数加法的计算方法时,借助人民币单位把小数转化成整数再计算,这种计算方法也能迁移到小数乘法、小数除法中。因此,在总结方法的时候,要关联之前的运算方法,让学生体会到这些运算方法中所蕴含的数学思想是一致的。
综上,学生运算能力的培养是一项长期的工程,教师在平时的教学中只有持之以恒地去做,才能收到理想的效果。
(责编 金 铃)
