基于神经网络的微波集成电路补偿模型设计

许 弘，刘 军，李志强，任 坤

(杭州电子科技大学射频电路与系统教育部重点实验室，浙江 杭州 310018)

0 引 言

随着集成电路工艺迈向后摩尔时代，以微米尺度2.5/3D异质异构互连工艺，实现多工艺平台设计的集成电路和传感、惯性等功能结构的微小化集成，逐步成为多功能电子系统高度集成设计和生产的新方向。以微米尺度互连实现系统的高密度集成，不同类型的集成电路芯片以及功能单元等，无法通过传统印制电路板(Printed Circuit Board，PCB)板级集成、灵活拆换、调试设计元件参数等方式实现系统设计优化，一次设计成功变得非常关键。由此，建立系统集成设计所需的多层级芯片、功能单元、互连结构等精确模型，并使用这些模型在电子设计自动化(Electronic Design Automation，EDA)工具中建立协同仿真设计流程，成为支持集成微系统设计的重要环节[1-2]。

射频集成电路是现代无线通信系统集成设计的重要组成部分。若射频芯片由系统设计单位自身设计完成，可采用设计工具(如Keysight Advanced Design System、Cadence SpectreRF)对设计原理图进行封装，从而得到可释放系统设计应用的宏模型。若射频芯片源于市场采购，芯片销售方通常只提供芯片产品手册等说明文档，只有部分测试数据支持用户芯片选型和小信号仿真，无法支持用户执行谐波等高阶功能的仿真。由于仿真设计结果和芯片实测结果存在一定的偏差，在高频应用上足以对系统集成设计造成一定的影响。因此，需引入模型补偿技术，补偿仿真模型偏差。人工神经网络(Artificial Neural Network，ANN)是一种常用建模框架，采用ANN的补偿模型建立微波器件、微波电路等的精确模型已有许多研究，Watson等[3]提出一种混合电磁ANN模型，用于微波器件补偿模型的建立。Bandler等[4-5]提出一种基于空间映射技术的ANN模型，用于补偿粗糙模型与精细模型之间的差值。随后，出现了大量的基于ANN模型的微波集成电路行为模型或补偿模型研究[6-9]。

本文提出一种射频集成电路宏模型的建模方法，以参考实际电路结构所建立的等效电路模型为基础，引入ANN技术，对初始建立模型和实测结果之间的误差进行补偿，形成一种快速建模方法。

1 理论分析

1.1 人工神经网络模型

图1 基本神经网络结构

人工神经网络是一种并行计算模型，由大量的节点(或神经元)相互联接构成。每个节点代表一种特定的输出函数，称为激活函数。每2个节点间的连接都代表1个通过该连接信号的加权值，称为权重。1个基本的神经网络包括1个输入层、多个隐藏层和1个输出层，其基本结构如图1所示。

神经网络的训练分为前向传播和反向传播[10]。在前向传播过程中，数据从输入层输入，乘以权重，由激活函数计算后得到相应节点的值，不断重复，直到数据传输到输出层。在反向传播过程中，神经网络的输出先与目标标签进行比较，计算出损失函数，再根据损失函数对神经网络的权重及偏置进行优化，最终得到有效的神经网络模型。

1.2 神经网络补偿模型

神经网络补偿模型用于补偿等效电路模型与实测数据之间的差值部分。为了使2个模型数据能够直接叠加，补偿模型应以并联的方式连接到等效电路模型上。Y参数是电路的导纳参数，反映端口间的传输导纳[11]。在二端网络的并联运算当中，相较于S参数，采用Y参数极大地简化了运算过程。因此，可以考虑先将S参数转换为Y参数，其转换表达式如下：

(1)

(2)

(3)

(4)

由于神经网络补偿模型补偿的部分为等效电路模型与实测数据之间的差值，因此，神经网络将两者的差值作为输出，以各项环境条件作为输入，补偿模型的训练框架如图2(a)所示。其中的神经网络补偿模型是一个基本的全连接神经网络，如图2(b)所示,包含1个输入层、1个输出层及1个隐藏层。其中输入层包含若干个输入节点，节点个数等同于输入变量个数；输出层包含8个节点，分别对应ΔY11，ΔY21，ΔY12和ΔY22的实、虚部，ΔY为等效电路模型与实测数据之间的差值；隐藏层包含50个节点(神经元)，以tanh函数作为激活函数。神经网络补偿模型可以表示为：

(5)

(6)

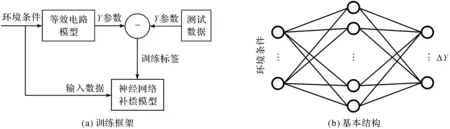
图2 神经网络补偿模型的训练框架及其基本结构

神经网络补偿模型采用均方误差(Mean Squared Error，MSE)损失函数，该函数用于表征神经网络训练误差，反映神经网络训练进程，其表达式为：

(7)

式中，y为神经网络输出值，y′为实测数据与模拟数据的Y参数差值。

用Adam优化器最小化损失函数，将训练好的神经网络补偿模型与等效电路模型并联，并联后的模型即为最终的电路模型[12]。

2 基于神经网络补偿模型的射频低噪声放大器建模

图3 芯片实物照片

本文实验对象为一片低噪声放大器电路芯片，经过拼接处理的芯片实物如图3所示,芯片采用台湾稳懋的PED25 0.25 μm GaAs pHEMT工艺设计制造，其工作参考电压为5 V，工作频段为6～13 GHz，5 V偏压环境下的静态工作电流为12 mA，增益典型值为24 dB，噪声系数约为1.3 dB，1 dB压缩点为2 dBm，输入输出驻波比分别为1.5和1.3。用于实验室系统集成仿真建模指标要求为：以偏置电压及小信号频率作为模型输入，S参数作为模型输出，采用均方根误差(Root Mean Squared Error，RMSE)来计算模型输出与实测数据误差，要求误差计算结果小于0.3，其计算公式如下：

(8)

式中，|S11j|表示第j个频率采样点对应的测试数据S11模值，|S′11j|表示第j个频率采样点对应的仿真数据S11模值，以此类推；n为频率采样点个数。本文实验以0.1 GHz为采样间隔，共计71个采样点。

若直接用芯片测试数据建立芯片行为模型，所建模型不具有芯片的基本物理信息，难以模拟未经芯片测试的所有功能。因此，本文尝试直接基于电路物理结构，结合芯片照片和芯片产品手册提供的电路结构等信息，建立芯片等效电路模型拓扑结构，如图4所示。芯片等效电路中的晶体管模型采用工艺设计包(Process Design Kit，PDK)自带模型模拟。在5 V偏压下，由芯片产品信息建立的等效电路模型的S21仿真结果与实际电路的测试结果对比如图5所示。

图4 等效电路模型示意图

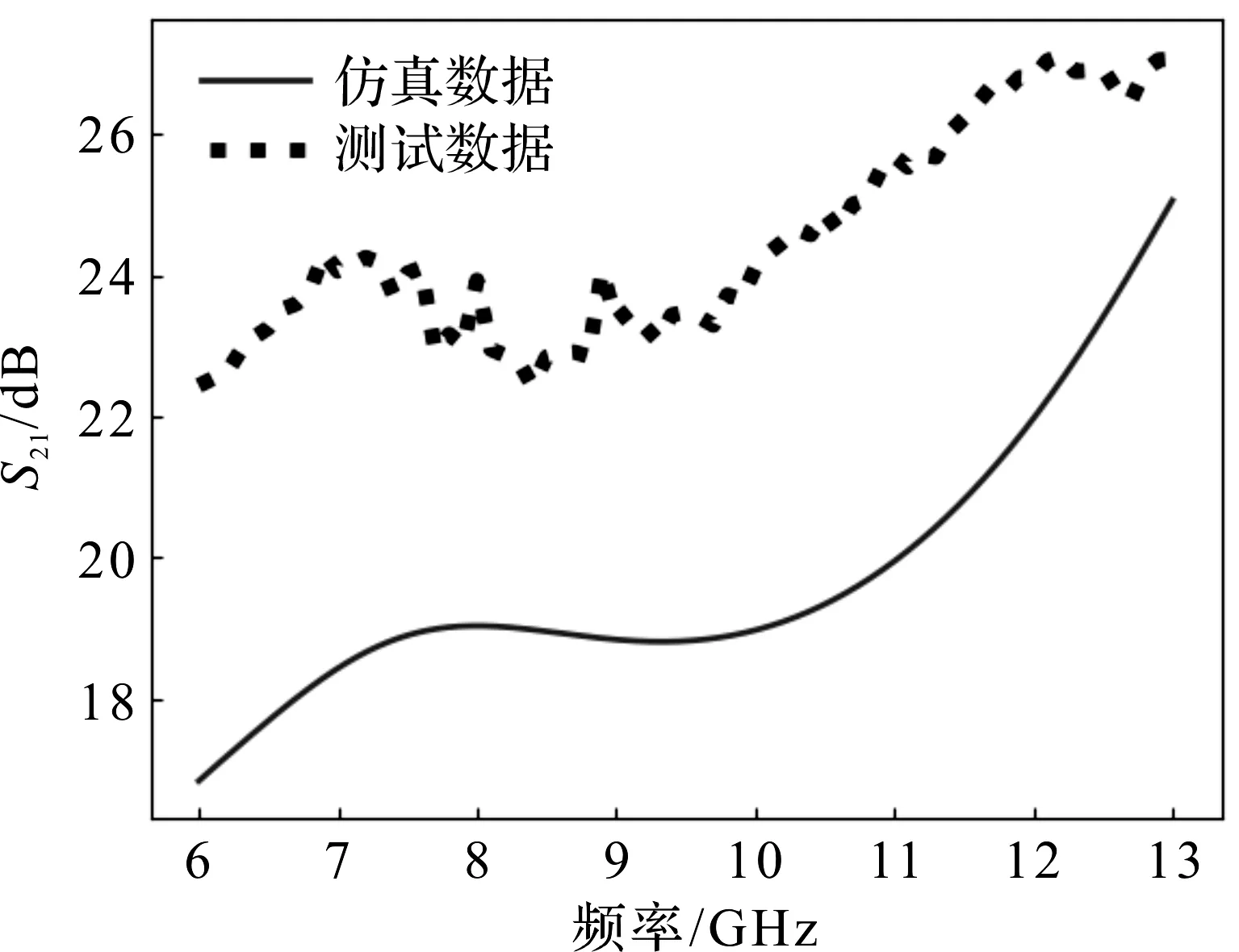
图5 初始等效电路模型数据对比

从图5可以看出，测试数据与仿真数据有较大的偏差，根据式(8)计算得到的误差值高达3.61，无法满足系统仿真精度的要求。模型与实测数据的误差主要由仿真器精度、元器件模型精度、环境误差、工艺误差等导致。因此，需对等效电路模型进行优化，调整电路各级之间的阻抗匹配，优化流程如图6所示。输入匹配通过调节电路模型输入端元器件参数、匹配信号源与输入端传输线的阻抗，优化输入端信号传输效率；输出匹配则通过调节输出端元器件参数，优化输出端信号传输效率；级间匹配通过调节各晶体管之间的元器件参数，优化各级信号传输效率；综合优化再次对各个元器件参数进行微调，使电路模型仿真结果尽量向测试数据靠拢。

图7 优化后等效电路模型数据对比

图6 等效电路模型优化流程图

经过参数优化后的等效电路模型在5 V偏压下的S21仿真结果如图7所示。与图5对比，模型仿真数据与测试数据之间的误差大幅度减小，能正确表征电路的带宽、趋势、放大能力等基本性能，仅在增益上仍有部分差距。通过式(8)计算得到优化后模型的误差值为0.868，相比初始模型已有大幅度改进，但仍未能满足指标要求。继续优化元器件参数已经很难进一步减小差值，故需通过建立补偿模型对其进行补偿。

神经网络补偿模型的建立流程如图8所示。

图8 神经网络补偿模型建立流程图

首先，进行参数转化，将仿真数据与测试数据全部转化为Y参数，并计算两者间的差值，将差值作为神经网络输出端的目标标签。其次，进行数据集划分，将转化后的数据集划分为训练数据集和测试数据集。训练集和测试集的数据分别如表1和表2所示，表中的r和i分别为实部和虚部的简写。

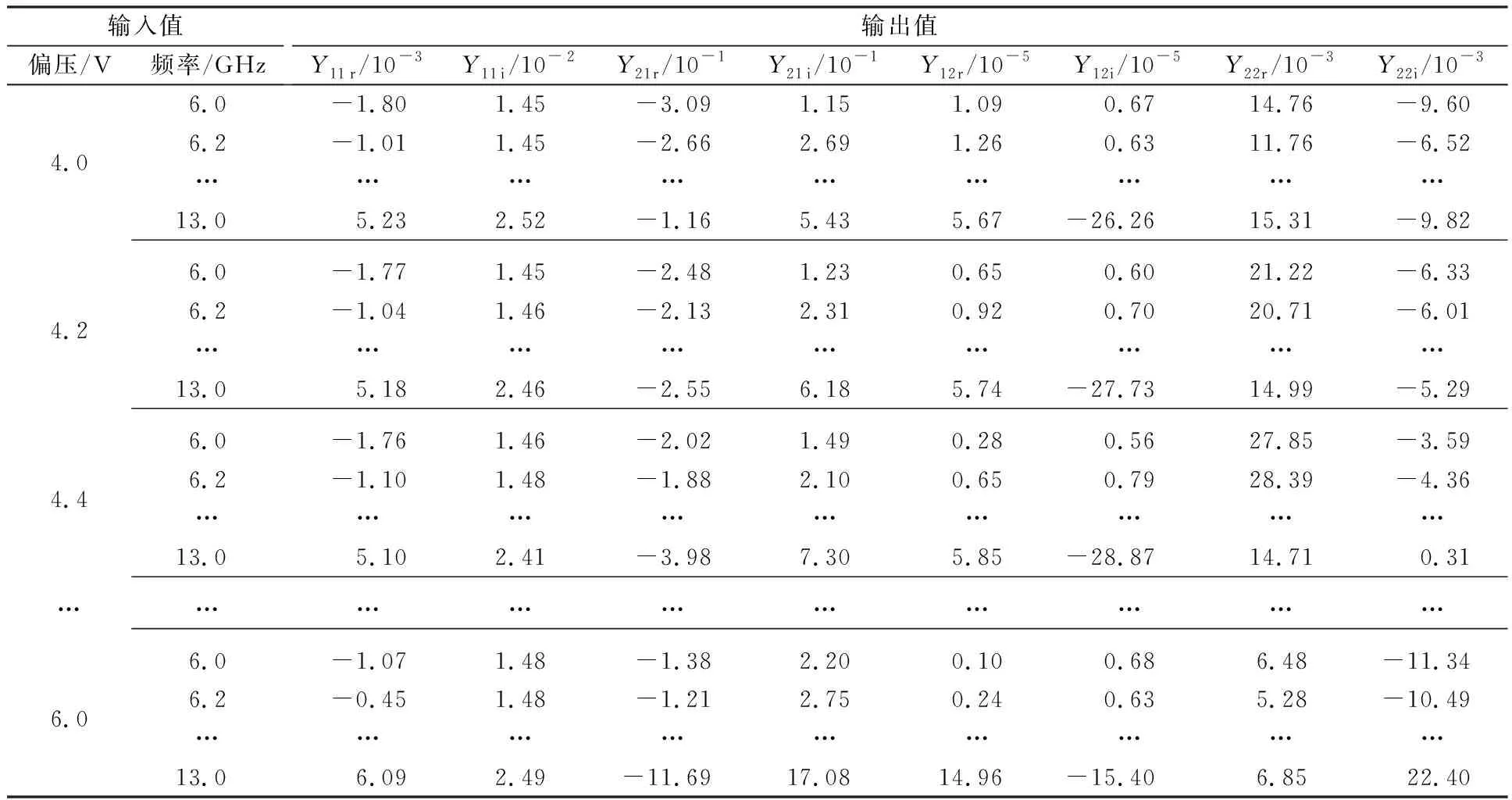
表1 神经网络补偿模型训练数据集

表2 神经网络补偿模型测试数据集

表3 神经网络训练过程误差表

从表3可以看出，随着训练轮数的增加，神经网络的误差值不断减小，最终训练集的误差为0.075。用测试集数据对神经网络进行验证，得到测试集误差为0.090。训练集的Y11实部差值预测结果和测试集的Y11虚部差值预测结果如图9所示。从图9可以看出，神经网络在训练集和测试集上均取得了良好的效果。

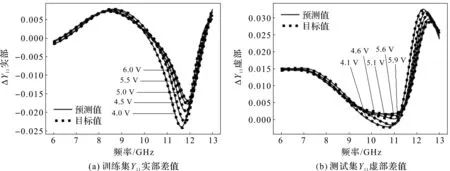
图9 训练集Y11实部差值和测试集Y11虚部差值的预测结果

将训练好的神经网络补偿模型与等效电路模型并联在一起，得到最终的电路宏模型。在5 V偏压条件下，运用ADS仿真软件对补偿后模型进行仿真，仿真数据与未补偿模型仿真数据以及测试数据的对比如图10所示。从图10可以看出，与未经补偿的等效电路模型仿真数据相比，模型补偿后的仿真数据与实际电路的测试数据匹配地更好，根据式(8)计算得到的误差值降低为0.274，达到建模指标要求。

图10 补偿前后模型仿真数据以及测试数据对比

3 结束语

针对模型仿真数据难以匹配电路实测数据的问题，提出一种新的宏模型建模方法，通过建立神经网络补偿模型补偿了等效电路模型与实测数据之间的差值。相较于传统等效电路建模方法，本文设计的补偿模型在保留传统模型物理特性的同时，弥补了传统模型精度不高的缺陷，提高了模型精度，提升了集成系统的仿真效率。但是，模型仿真结果中仍存在少量拟合误差，建立模型所依赖的测试数据也包含部分测试误差，对集成系统的仿真精度造成一定影响，这是今后需要进一步解决的问题。