热解炭表面复合型裂纹初始起裂角研究

刘 刚，王丽雅，查 潇，张建辉

(杭州电子科技大学机械工程学院，浙江 杭州 310018)

0 引 言

热解炭具有耐磨、耐腐蚀以及优异的生理相容性等特点，自1969年首次使用以来，无论是作为整体材料还是作为石墨基体的涂层，已成为大多人工机械心脏瓣膜的首选材料[1]。植入人体的人工机械心瓣瓣片表面长期承受血流的循环冲击，由于空化气蚀等原因，在涂层表面不可避免地出现半椭圆形微小裂纹[2]。这些微小裂纹可能对宏观裂纹的扩展产生重大影响，甚至威胁患者的生命[3]，因此，对热解炭涂层表面微裂纹扩展的研究至关重要。目前，国内对热解炭涂层断裂性能研究方面的报道较少，国外相关研究人员对热解炭涂层材料裂纹扩展进行了较多的研究，如Ritchie等[4]使用电伺服液压测试系统对热解炭包覆石墨复合材料进行疲劳裂纹扩展试验，研究人工心瓣的断裂韧性与疲劳裂纹扩展速率；Ryder等[5]运用损伤容限设计方法对人工心脏瓣膜组件进行疲劳寿命预测。断裂力学中，根据裂纹所受载荷形式将裂纹分为3种类型：张开型(Ⅰ型)、滑开型(Ⅱ型)及撕开型(Ⅲ型)[6]。人工心瓣瓣片在心脏内作开合运动时，热解炭涂层裂纹扩展面与血流载荷之间的夹角时刻变化，瓣片表面裂纹受到不同方向血流的载荷作用，涂层不是单纯的Ⅰ型或Ⅱ型断裂，因此研究人工心瓣热解炭涂层表面Ⅰ-Ⅱ复合型裂纹更为合理。裂纹初始起裂角是研究裂纹扩展的重要参数，在预测裂纹扩展路径与处理止裂问题上具有重要意义[7]。本文采用有限元分析软件ABAQUS，结合断裂分析软件FRANC3D仿真求解热解炭试样表面微裂纹初始起裂角，讨论裂纹倾斜角和深度对裂纹初始起裂角的影响，为后续研究热解炭涂层裂纹扩展及其寿命预测提供理论依据。

1 理论基础

植入人体心脏的人工心瓣瓣片表面长期承受血流的循环冲击作用，由于空化气蚀等原因，在瓣片表面出现物理性微小裂纹(小于500 μm)。一般情况下，60 kg成人的心脏瓣膜瓣内径入口瓣为25 mm、出口瓣为23 mm[8]，裂纹尺寸远小于结构尺寸，可以将含裂纹人工心瓣表面等效为含中心半椭圆形表面裂纹的无限大平板。断裂分析软件FRANC3D中，计算裂纹初始起裂角的方法有最大拉应力准则(Maximum Tensile-Stress，MTS)、最大剪应力准则、广义应力和应变能释放率等，本文采用MTS准则计算裂纹初始起裂角。Erdogan等[9]于1963年首先提出一定载荷作用下含裂纹平板产生裂纹失稳扩展现象的判据，即MTS准则。主要包括两个方面：(1)裂纹在裂纹尖端周向拉应力最大的方向θ0起裂扩展；(2)当沿θ0方向上距裂纹尖端距离为临界值rc的周向力σθ超过临界应力σc时，裂纹开始起裂扩展。表示为：

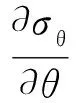
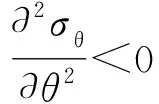
σθ=σc

(1)

裂纹尖端应力场在极坐标下采用Williams特征极数展开可得：

(2)

(3)

式中，r，θ为极坐标，其原点位于裂纹尖端，σr为极坐标下裂纹尖端径向应力，σθ为周向拉应力，裂纹在周向拉应力最大方向上起裂扩展。KⅠ，KⅡ分别表示Ⅰ型和Ⅱ型应力强度因子(Stress Intensity Factors，SIFs)。结合式(1)—式(3)可以得到裂纹初始起裂角的计算公式[10]：

(4)

2 模型参数与网格划分

2.1 模型几何参数

ABAQUS是一套具有强大功能的工程模拟有限元软件，从简单的线性分析到复杂的非线性分析都可以用它来解决[11]。在ABAQUS中建立3D几何模型如图1所示，模型为中部含有半椭圆形裂纹的板块，其中2W=2H=10a，H=5t，a和b为半椭圆轴长，β为裂纹面与水平方向所成倾斜角。模型材料为各向同性热解炭，弹性模量E=28 GPa，泊松比ν=0.3。模型上下表面分别施加方向相反的载荷σ=10 MPa，其中Ⅰ型裂纹载荷与模型端面垂直，Ⅱ型裂纹载荷与模型端面平行[12]。

图1 几何模型与半椭圆形裂纹

2.2 网格划分

通过FRANC3D读取有限元模型，采用20节点六面体二次缩减单元(C3D20R)对模型进行全局网格划分，由于裂纹尖端存在奇异点，半椭圆形裂纹尖端采用1/4节点技术进行自适应网格划分以提高计算精度，带预制裂纹的网格模型如图2(a)所示。进行准静态裂纹扩展分析时，为了确定裂纹前缘不同位置处的裂纹初始起裂角，在半椭圆形裂纹前缘选取21个等距节点，半椭圆形裂纹形状左右对称，左边11个节点如图2(b)所示。

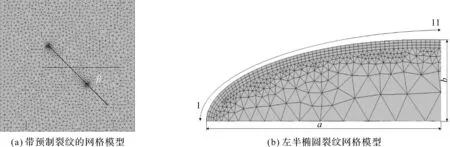
图2 网格划分模型

3 仿真实验结果与分析

根据应力强度因子理论，影响应力强度因子的因素主要包括裂纹形状、裂纹位置以及裂纹数目等，继而影响裂纹初始起裂角[2]。本文通过改变裂纹倾斜角β和裂纹短半轴长度b来研究不同倾斜角与深度裂纹对热解炭涂层半椭圆形中心裂纹初始起裂角的影响。

3.1 可靠性验证

结合应力强度因子手册[13]中基于实验基础的理论值和式(4)可以计算得到裂纹初始起裂角，但是，由于实验条件的限制，理论值KⅠ，KⅡ有限且不能满足不同裂纹倾斜角与深度下裂纹初始起裂角的求解，因此，用有限的理论数据来验证FRANC3D仿真求解的可行性，继而通过仿真求解不同裂纹情况下的裂纹初始起裂角。Ⅱ型裂纹中，保持裂纹深度不变，不同裂纹倾斜角下的半椭圆形中心裂纹尖端初始起裂角仿真值与理论计算值如表1所示。

表1 FRANC3D中裂纹初始起裂角仿真值与理论值对比

由表1可知，裂纹初始起裂角仿真值与理论值误差在5%以内，说明基于ABAQUS和FRANC3D软件对热解炭涂层裂纹初始起裂角的仿真模拟具有可行性。

3.2 裂纹倾斜角对半椭圆形裂纹初始起裂角的影响

保持裂纹深度不变，倾斜角β的范围取0°～90°，每隔15°重新建模仿真分析。Ⅰ型裂纹初始起裂角随裂纹倾斜角β的变化规律如图3(a)所示。由图3(a)可以看出：(1)倾斜角β=0°时，裂纹初始起裂角为0，即裂纹沿着初始开裂方向扩展；(2)裂纹深度保持不变时，同一倾斜角下的裂纹前缘初始起裂角关于裂纹前缘中心节点对称，方向相反；(3)随着裂纹倾斜角逐渐增大，以裂纹前缘中心节点为中心，裂纹初始起裂角向裂纹两端延伸，呈单调增大的趋势，即裂纹前缘越接近材料表面，裂纹尖端起裂角越大，这主要是由于裂纹前缘不同节点处SIFs不同，越靠近裂纹尖端处的SIFs对有限元模型边界和载荷条件越敏感，受到的影响也就越大[14]。图3(b)为裂纹倾斜角β=45°时裂纹前缘不同位置处的KⅠ，KⅡ值，可以看出，KⅠ关于裂纹前缘中心对称，KⅡ关于裂纹前缘中心互为相反数，结合式(4)可以论证，当裂纹深度保持不变时，同一倾斜角下的裂纹前缘初始起裂角关于裂纹前缘中心节点对称，裂纹扩展方向相反。

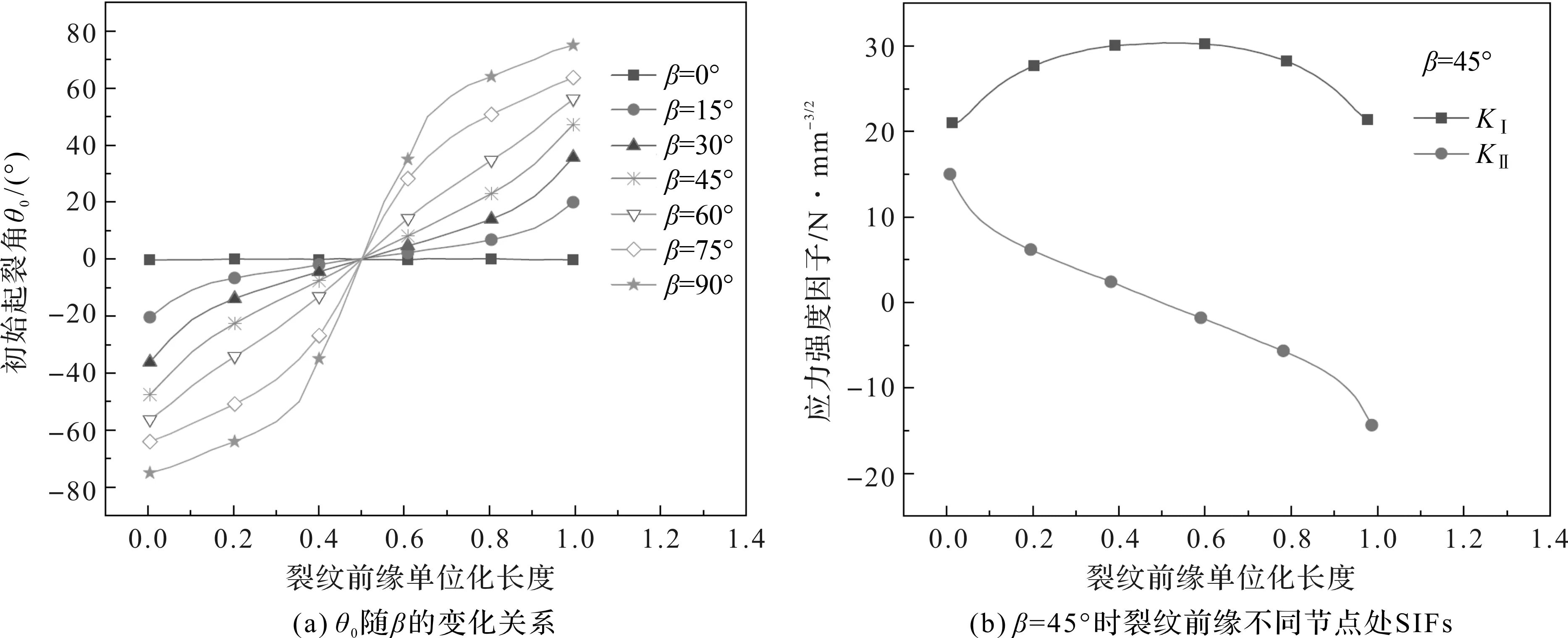
图3 倾斜角β变化时，Ⅰ型裂纹初始起裂角θ0及β=45°时裂纹前缘SIFs分布

Ⅱ型裂纹初始起裂角随裂纹倾斜角β的变化规律如图4(a)所示。由图4(a)可知：(1)β为0°和90°时，初始起裂角稳定在70.5°，方向相反；(2)裂纹深度保持不变时，同一倾斜角下的裂纹前缘初始起裂角关于裂纹前缘中心节点对称，方向相反；(3)裂纹倾斜角β=45°时，除裂纹两端初始起裂角相对较大外，其余位置初始起裂角接近于零。随着裂纹倾斜角β偏离45°，初始起裂角逐渐变大，且偏离程度越大，初始起裂角越大。图4(b)为裂纹倾斜角β=45°时调用ABAQUS进行裂纹有限元仿真分析得到的应力云图，从图4可以看出，裂纹前缘应力分布关于裂纹中心对称，且在裂纹尖端处存在明显的应力集中现象，达到229.8 MPa。

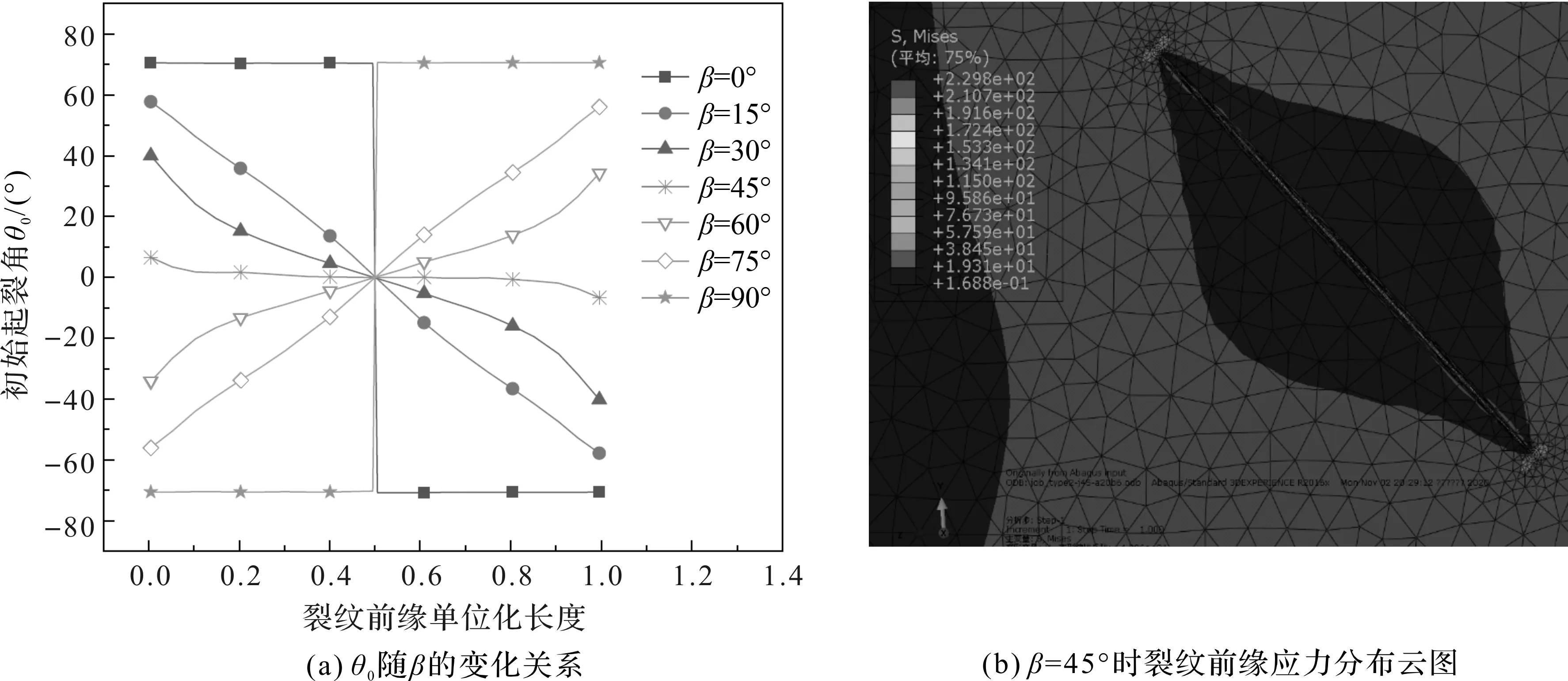
图4 倾斜角β变化时Ⅱ型裂纹初始起裂角θ0及β=45°时裂纹前缘应力分布

3.3 裂纹深度对半椭圆形裂纹初始起裂角的影响

保持裂纹倾斜角β=45°以及半椭圆形裂纹长半轴a的长度不变，改变短半轴b的长度，使得b/t在0.2～0.8之间变化，每隔0.2数量级重新建模仿真分析。β=45°时不同裂纹深度下的裂纹初始起裂角的分布情况如图5所示。从图5可以看出：(1)同一深度下的Ⅰ型和Ⅱ型裂纹前缘初始起裂角关于裂纹前缘中心节点对称，方向相反，且在裂纹尖端处取得最大值，在裂纹前缘中心取得最小值。(2)随着裂纹深度(b/t)的增大，靠近模型表面的Ⅰ型和Ⅱ型裂纹初始起裂角变化速率呈递减趋势。b/t=0.2，即裂纹深度最小时，靠近模型表面的裂纹初始起裂角变化速率最大，说明裂纹深度越小，对模型表面裂纹初始起裂角影响越大。(3)不同裂纹深度下的Ⅱ型裂纹初始起裂角分布较Ⅰ型裂纹更为贴近，说明裂纹深度对Ⅰ型裂纹初始起裂角的影响程度大于Ⅱ型裂纹。

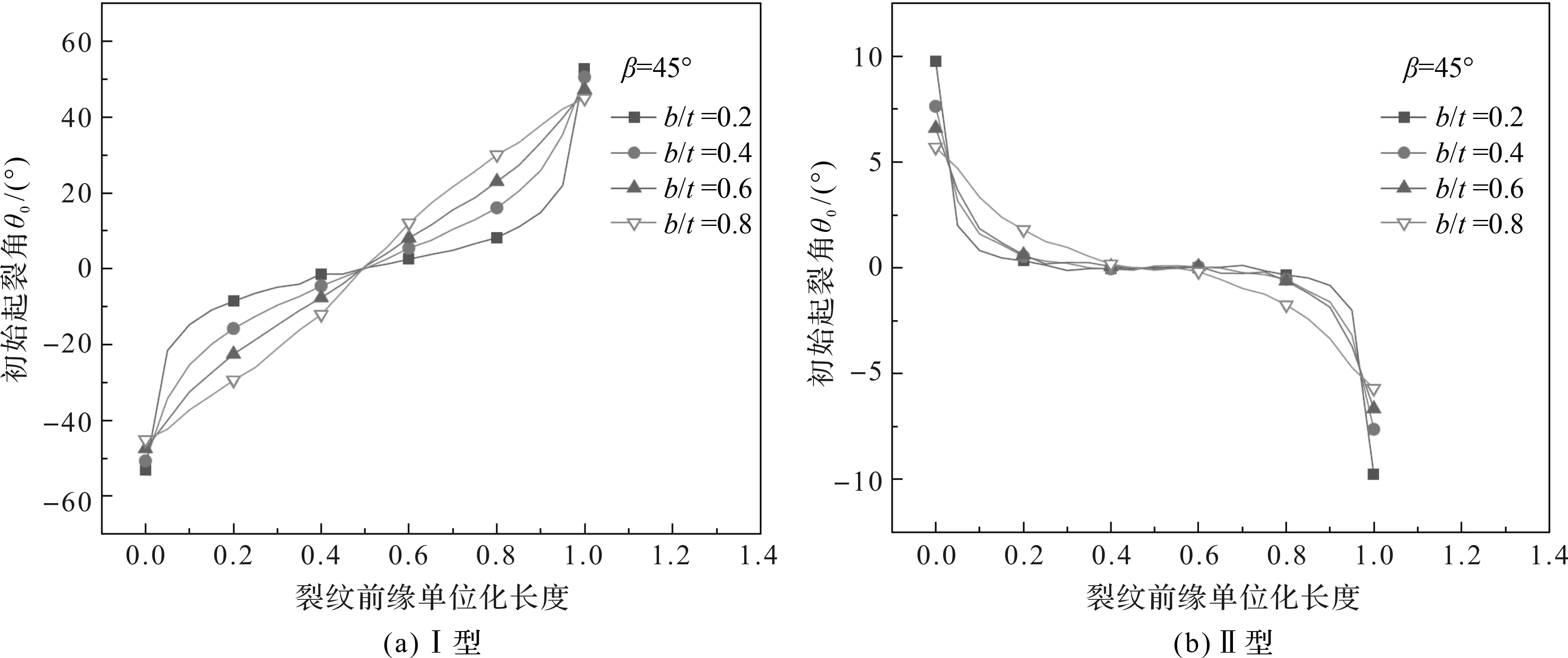
图5 β=45°，不同深度裂纹Ⅰ，Ⅱ型裂纹初始起裂角分布

4 结束语

本文运用ABAQUS有限元分析和FRANC3D断裂分析软件对人工心瓣热解炭涂层表面半椭圆形中心裂纹初始起裂角展开研究，验证了ABAQUS有限元和FRANC3D断裂分析软件联合仿真模拟的合理性与可靠性。裂纹初始起裂角在裂纹前缘中心取得最小值，在裂纹尖端取得最大值，说明在裂纹扩展过程中，裂纹尖端处的角度改变量大于裂纹中心处。裂纹深度和裂纹倾斜角均对裂纹初始起裂角产生不同程度的影响。在此基础上，后续将对热解炭涂层裂纹扩展及寿命预测展开进一步研究。