深度学习中的预条件动量梯度算法
2021-09-29张亮亮喻高航
张亮亮,喻高航
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
深度学习(Deep Learning,DL)[1]在许多实际领域中取得了显著的成功,如图像分类[2]、目标检测[3]和人脸识别[4]等,但在大规模数据集上训练深度神经网络仍然很费时。一阶优化算法是深度学习中广泛使用的方法,如动量梯度算法。常用的动量梯度算法主要有重球法(Heavy Ball Method,HB)[5]和Nesterov加速梯度法(Nesterov’s Accelerated Gradient Method,NAG)[6]。当动量方向为有利方向时,动量梯度算法通常能够加速优化,但是,动量项在迭代过程中积累过多历史梯度信息导致超调,造成迭代过程中的震荡现象[7],在一定程度上阻碍了算法的收敛速度。“比例—积分—微分”优化控制器(Proportional-Integral-Derivative Controller,PID)[8]是一种通过控制系统误差来调整系统的反馈控制方法,可以有效克服超调现象,具有鲁棒性,已广泛应用于无人驾驶和智能机器人等实际控制领域。文献[9]提出一种加速深度神经网络优化的PID算法,在PID控制器与大规模优化算法之间建立联系。实际应用中,PID控制器中的微分项通常采用一阶差分近似,在优化过程中无法有效利用二阶信息。为此,本文采用拟牛顿方程,提出一类预条件动量梯度算法。
1 深度学习优化模型
1.1 经验风险最小化
深度学习中常见的一类学习问题是回归与分类等监督学习问题,提供了包含输入数据和带有标签的训练数据集。对已知样本构成的训练集{(x1,y1),(x2,y2),…,(xn,yn)},监督学习通常需要求解经验风险最小化(Empirical Risk Minimization,ERM)[10]模型:
(1)
通过优化模型参数θ,进而预测未知样本x的标签值y,其中li(θ)是第i个样本关于θ的损失函数,n是样本总数,xi∈Rd是第i个样本的输入特征向量,d是特征向量维数,yi∈R是第i个样本的标签(或目标)。
1.2 优化算法
求解模型(1)最常用的是一阶优化算法,比如梯度下降法(Gradient Descent Method, GD):
(2)
式中,α是学习率,一般取常数,k是迭代次数。梯度下降法的算法简单,易于实现,但收敛速度慢。为了加速训练神经网络,目前深度学习领域常用的是随机梯度算法或动量梯度算法,其中经典的动量方法包括重球法[5]:
(3)
其迭代格式可写为:
(4)
另外一种常用的动量梯度方法是Nesterov加速梯度法[6]:
(5)
两种动量方法中的参数β∈(0,1)决定动量项的权重。
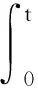
(6)
离散形式为:
(7)
式中,e(t)是系统误差,t是系统响应时间,kp,ki,kd是PID的权重系数,分别控制PID中P项,I项和D项。
对式(4)和式(5)中第1行公式两边同时除以βk+1,得到:
(8)
对式(8)从k+1到1列举并相加可得:
(9)
将式(9)代入式(4)和式(5)中的第2行公式,可得:
(10)
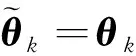
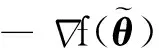
2 预条件动量梯度算法
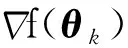
(11)
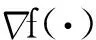
(12)
令θ=θk-1,有:
(13)
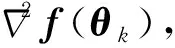
(14)
当kd=0时,式(14)可退化为HB算法;当kd≠0,令Qk=(βI/kd-Bk),式(14)改写为:
(15)
称式(15)为预条件动量梯度算法(Preconditioned Momentum Gradient Algorithm,PMG)。
预条件因子Qk中Bk的更新迭代,可以采用拟牛顿算法中常用的BFGS修正公式[12]:
(16)

式(14)进一步写为:
(17)
基于BFGS的预条件动量梯度算法的主要步骤如下。

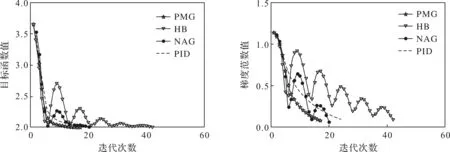
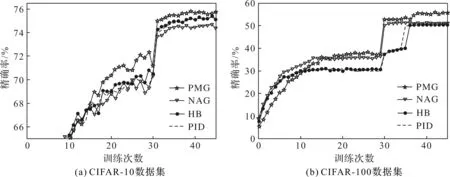
输入:目标函数f(θ),初始迭代点θ0∈Rn,初始迭代矩阵B0=I(I∈Rn×n单位矩阵),最大迭代次数K,容忍误差ε,参数α>0,β∈(0,1),kd>0;计算梯度值Δf(θ0),如果不满足终止条件,用最速下降法计算θ1=θ0-αΔf(θ0),计算Δf(θ1),置k=1。当Δf(θk)>ε或k PMG算法在每次迭代中保持2个序列的更新,即{Vk},{θk}。当kd=0时,PMG算法退化为HB算法。与PID算法相比,PMG算法中{Bk}的计算能够较好地利用目标函数的二次信息。预条件的选取还可以有其他不同的方式,如DFP修正公式、对角矩阵Bk=diag(λ1,λ2,…,λn)或与谱投影梯度方法[13]类似的仿射单位矩阵等。 引理[14]设{Fk}k≥0是一个非负实数序列,且满足条件Fk+1≤a1Fk+a2Fk-1,∀k≥1,其中a2≥0,a1+a2<1且系数至少有1个是正的。那么序列{Fk}k≥0对所有的k≥1满足关系式 Fk+1≤qk(1+δ)F0 (18) 定理设目标函数f(θ)是μ-强凸的和L-利普希兹连续的,θ*∈Rn是函数f(·)的全局最优点,则算法PMG产生的序列{θk}k≥1满足: 可以证明以下不等式成立, (19) (20) (21) 根据式(19)—式(21),可得: (22) 因为f(θ)是μ-强凸的和L-利普希兹连续的,由凸优化理论有: (23) 将式(23)代入式(22),可得: (24) (25) 当PMG算法中参数α,kd满足 为了验证本文提出的PMG算法的有效性,分别在一些小规模的测试函数和大规模的CFIAR数据集上对PMG算法、PID算法、HB算法和NAG算法进行数值对比实验。 例3f3(x)=-[cosx1+1][cos2x2+1]是一个非凸二维三角函数,初始点[-2,1]。 例4f4(x)=sin(x1+x2)+(x1-x2)2-1.5x1+2.5x2+1是多峰函数,初始点[-10,2]。 关于PMG算法的参数设定为:步长α使用回溯法,初始步长α=0.5,动量参数常设为β=0.9,根据文献[8]和文献[15]提出的PID参数选择方法选取参数kd。实验运行环境为Windows 10操作系统下的MATLAB 2016b,配置内存为Intel Core i7-3667U 8GB的笔记本。记录4种算法的终止迭代次数、运行时间和算法的终止误差,结果如表1所示。 表1 不同动量梯度算法求解算例的结果 从表1可以看出,与HB算法和NAG算法相比,PID算法比常用的动量梯度方法更有效。由于PMG算法能够较好地利用目标函数的二次信息,在4种算法中,PMG算法的迭代次数和运行时间都有一定的优势,说明PMG算法可以有效提升算法的效率。 为了更直观比较算法效率,针对测试函数例1的迭代收敛过程,分别从目标函数值和梯度范数值两个角度说明变化情况,结果如图1所示。 图1 不同算法测试部分函数随迭代步数变化的情况 从图1可以看出,HB算法与NAG算法都有明显的震荡,而PMG算法和PID算法均能克服超调现象,其中PMG算法表现更好。 图2 不同算法训练数据集精度随迭代变化的情况 从图2可以看出,PMG算法的预测精度最高,表明高阶信息的有效利用使得PMG算法的性能得到较大提升。 动量梯度算法因积累过多历史梯度信息会导致超调问题,阻碍算法的收敛。针对这个不足,本文将预条件因子与动量梯度法相结合,提出一种预条件动量梯度算法,在提高算法效率的同时克服了超调问题,有效改善了迭代过程中出现的震荡现象。但是,预条件因子生成方法是多样化的,选取合适的预条件会花费额外的时间,后期将针对最优预条件因子的选取问题展开进一步研究。3 收敛性分析

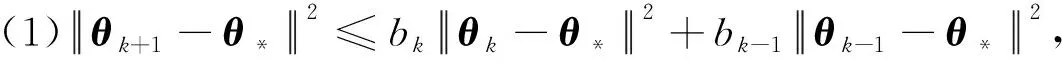
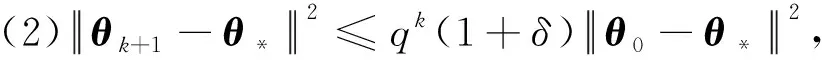
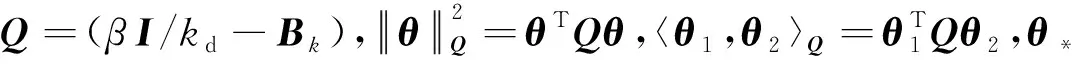

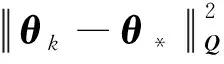

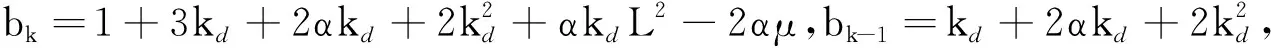
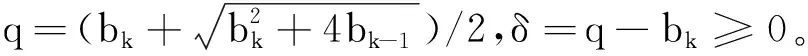
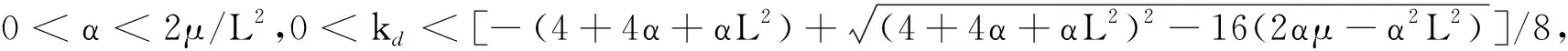
4 数值实验
4.1 测试函数
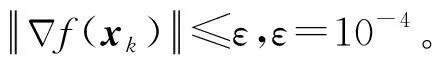

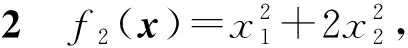
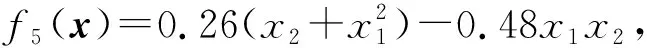

4.2 CFIAR数据集

5 结束语
