一类热弹耦合问题的奇摄动解

帅 欣，包立平

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

耦合热弹性问题是热弹性力学中最一般的问题。它考虑温度同变形的相互作用，即不但温度会产生变形，而且变形也要产生或消耗能量，从而影响温度。这样，在热传导方程中有一个包含应变的附加项，称为温度场和应变场的耦合项。热传导方程和热弹性方程不再是独立的，必须联立才能求解温度、位移和应力。文献[1]采用直接有限元方法来求解基于L-S型广义热弹性理论的窄条薄板受热冲击作用的动态响应问题，结果表明，该方法在求解L-S型广义热弹性耦合的一维问题数值解上具有很高的精度。文献[2]应用非Fourier热传导定律构建了单层材料中温度场模型，得到内外解的存在唯一性，再通过余项估计得到渐近解的一致有效性，从而得到无界域上温度场的分布，描述了非Fourier温度场的具体形态。文献[3]分析了求解热传导方程的几种差分格式，并介绍使用MATLAB编程求解偏微分方程的方法。文献[4]建立了斜拉桥钢索二阶双曲型偏微分方程模型，讨论了加权平均格式差分方程解的收敛性，并运用MATLAB对差分方程的数值解进行求解。文献[5]针对一类带小参数的二阶双曲型方程，提出基于有限差分格式的自适应移动网格方法，给出具体的移动网格算法，改进了均匀网格上求解的结果。文献[6]讨论了具有扩散，微温度和微浓度的圆的一个热弹性边值问题的显式解。本文讨论一类热弹耦合模型并将其简化为求解热传导方程和双曲方程，再求解出相应方程的内外解，最后通过数值分析得出首项的数值解。

1 模型建立

一类热弹耦合模型如下：

(1)

(2)

式中，(x,t)∈Ω，ε为正参数，φ1(x)，φ2(x)，φ3(t)，φ4(t)，α1(x)，α2(x)，α3(t)，α4(t)为已知任意阶连续可微函数，同时假设：

(1)Ω=[0,L]×[0,T]，R=[0,L]；

(2)k为热传导系数，ρ为密度，a,b为常数，记a/ρ=m2,b/ρ=c。

2 形式展开

奇摄动关于方程解可以展开成含小参数的幂级数形式的正则部分和边界层部分理论，对方程(1)的解做正则展开得到正则部分解：

T(x,t,ε)=T0(x,t)+εT1(x,t)+ε2T2(x,t)+…

(3)

比较ε同系幂系数，可得：

(4)

(5)

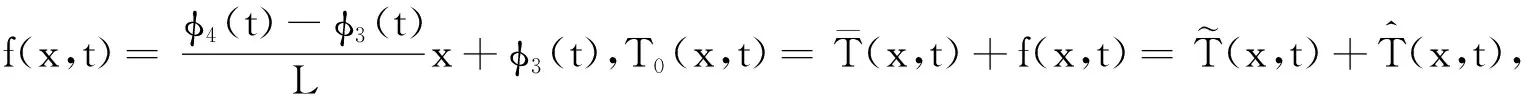
(6)

(7)

(8)

类似方程(4)的求解，可对方程(5)进行求解。给出式T(x,t)的合成展开式：

(9)

代入方程(1)得：

则有p0(x,0)=T0,t(x,0)-φ2(x),pj+1(x,0)=pj,t(x,0)+Tj,t(x,0)，再比较ε同次幂系数，得到：

(10)

(11)

类似方程(4)、方程(5)，可对方程(10)、方程(11)求解。再对方程(2)的解作正则展开，得到：

(12)

将式(12)代入方程(2)，比较ε同次幂系数，得到：

(13)

(14)

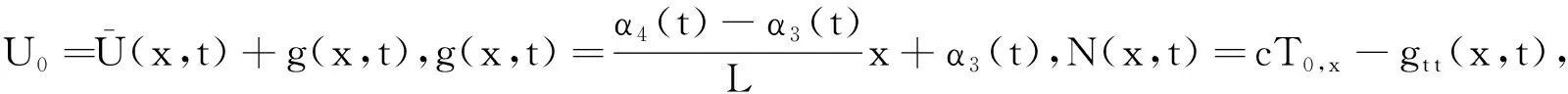
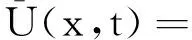
(15)

类似方程(13)的求解，可解出方程(14)。对方程(2)的解U(x,t)作合成展开有：

(16)

比较ε的同次幂系数，可得：

qj+2=2qj+1,t+m2qj,xx+cpj,x-qj,t t

(17)

此时可得q0(x,t)=q1(x,t)=0。

3 余项估计

定理1方程(1)的解

T*(x,t,ε)=T0+…+Tnεn+p0εe-t/ε+…+pn-1εne-t/ε+Rεn+1

的余项R满足：

证明首先考虑方程(1)的解

T*(x,t,ε)=T0+…+Tnεn+p0εe-t/ε+…+pn-1εne-t/ε+Rεn+1

(18)

将余项R代入方程(1)得到：

(19)

式中，G(x,t)=-Tn,t t-pn-1,t te-t/ε，由前面对方程(5)、方程(11)求解可知G(x,t)在闭区域Ω上连续，则存在常数M1，使得∬ΩGdxdt≤M1，将方程(19)等式两边同乘2Rt，并在区域Ω上积分可得：

(20)

经过化简可得：

(21)

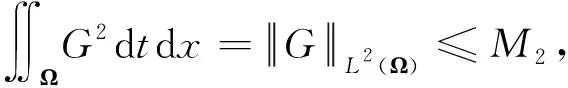
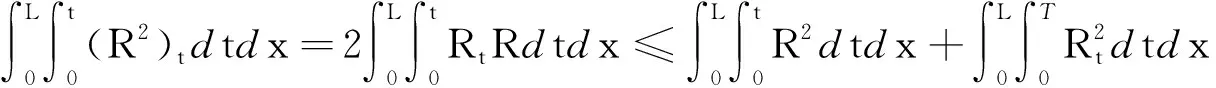
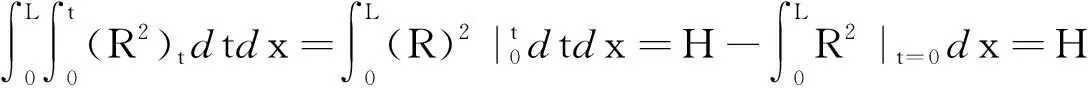
(22)

(23)

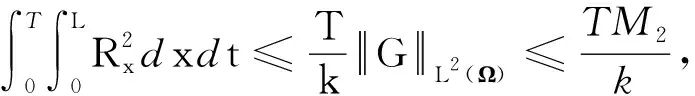
(24)

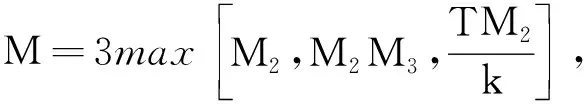
定理2方程(2)的解

U*(x,t,ε)=U0+…+Unεn+q0εe-t/ε+…+qn-1εne-t/ε+Sεn+1

的余项S满足：

S≤cM(x,t)∈Ω

证明首先将方程(2)解

U*(x,t,ε)=U0+…+Unεn+q0εe-t/ε+…+qn-1εne-t/ε+Sεn+1

(25)

的余项S代入方程(2)，可得：

(26)

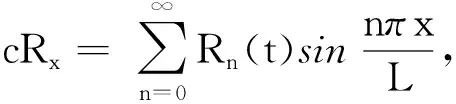
4 数值分析

在区域Ω上定义均匀网格为：

xi=ihi=0,1,2,…,M,M=L/h
tj=jτj=0,1,2,…,N,N=T/τ

(27)

(28)

采用中心差商将方程(13)化为：

(29)

5 数值算例

令m2=1，k=c=1，h=0.01π，τ=0.01，L=π，T=1，取T0=e-x+t，p0=sin(x)et，U0=e-x+t，Ω=[0,π]×[0,1]，分别得出其边界条件。首项误差图形如图1所示。

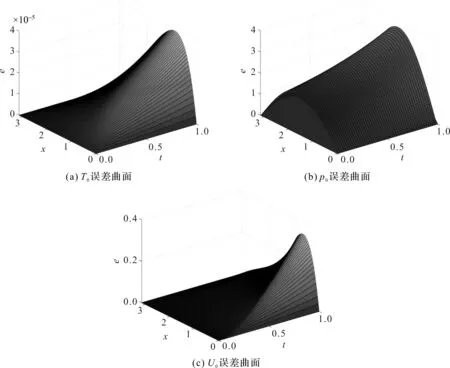
图1 首项误差图

通过图1可以看出，对于T0，U0数值差分格式得出的数值解误差在可接受范围内，当选取步长更小时，误差会更小，由此得出其数值解是有效的。虽然p0的误差较大，但是根据所构造渐近解形式，系数ε可使得其值很小，不影响整体解。

6 结束语

本文讨论一类热弹耦合方程在有界区域上带边界条件的问题。在温度场基础上，考虑弹性场，解耦温度场与弹性场方程，并通过求解温度场方程，得出弹性场变化。后期将针对不能解耦情况下的一维热弹耦合问题展开研究，继而探究二维、三维情形，并分析间断热传导系数下的热弹耦合问题。