变频调速异步电动机电磁转矩计算方法
2012-11-22王崇任
王崇任,韩 力,李 辉
(重庆大学,重庆400044)
0 引 言
由于异步电动机具有结构简单、运行可靠、价格低廉、无失步或退磁等一系列优点,因此在国民经济各行各业应用广泛。近年来,随着电力电子技术的快速发展以及大容量变频器的出现,异步电动机被越来越广泛地应用于各种变频调速系统中。变频调速系统的出现,对异步电动机的电磁设计提出了新的要求。
常规异步电动机的电磁设计仅需要对额定转矩、最大转矩和起动转矩进行校核计算[1],而变频调速异步电动机需要在相当宽的频率范围内变速运行[2]。因此,传统的异步电动机电磁设计程序已无法满足变频调速异步电动机电磁设计的需要。
π 型等效电路模型计算精度高,但计算程序复杂、计算速度慢[3-4];Г 型等效电路模型计算简单,但计算精度低[1,5]。变频调速异步电动机电磁在设计时,需要校核计算不同工况下多点上的电磁转矩。为了兼顾计算精度和计算速度的要求,有必要对π型和Г 型等效电路计算模型进一步深入研究,并在此基础上进行合理选用。
针对变频调速异步电动机不同频率段稳定运行电磁转矩快速、准确计算的问题,本文首先对T 型、π 型、Г 型等效电路及其衍生出的其它等效电路计算模型进行理论分析和对比,并结合变频调速异步电动机的运行特点,给出了各种等效电路计算模型的特点和适用范围,通过与π 型等效电路精确计算模型的对比,说明了各种模型和算法的适用范围。
1 电磁转矩计算
三相异步电动机稳态电磁转矩的计算需要用到等效电路。下面,首先对等效电路模型及其特点进行分析。
1.1 等效电路模型
众所周知,反映异步电动机内部电磁关系的精确等效电路模型为T 型等效电路,如图1 所示[3-5]。
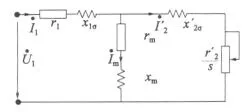
图1 T 型等效电路模型
其中images/BZ_61_342_368_394_439.png和images/BZ_61_458_366_495_434.png 分别为定子绕组的相电压和相电流;images/BZ_61_239_457_279_530.png 为激磁电流;images/BZ_61_542_456_590_533.png为转子绕组相电流的归算值;r1和x1σ分别为定子绕组的电阻和漏抗;r2′和x2′σ分别为转子绕组的电阻和漏抗归算值;rm和xm分别为激磁电阻和激磁电抗;s 为转差率。
为了准确反映激磁支路的物理本质,可将串联的激磁支路转化成由铁耗电阻rFe和磁化电抗xμ并联,从而得到π 型等效电路[3-4],如图2 所示。
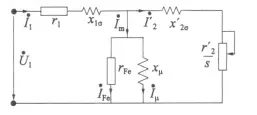
图2 π 型等效电路模型
经推导,将T 型等效电路转化为准确Г 型等效电路,如图3 所示。其中校正系数[5]:

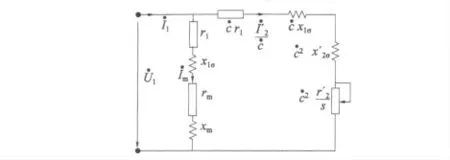
图3 准确Г 型等效电路模型
准确Г 型等效电路与T 型等效电路、π 型等效电路完全等价,只是电路的拓扑结构有所区别。在图3 中,由于校正系数为复数,不便于计算。在额定工频情况下,考虑到x1σ>>r1和xm>>rm,因此可将校正系数近似用一个标量来代替[1,5]:

将式(2)代入图3,由此可得到较准确Г 型等效电路模型[5],如图4 所示。
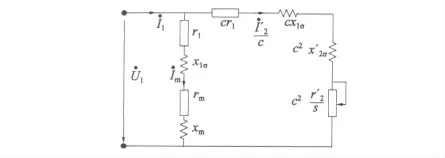
图4 较准确Г 型等效电路模型
根据较准确Г 型等效电路模型,经推导可得到异步电动机的电磁转矩计算式[5]:
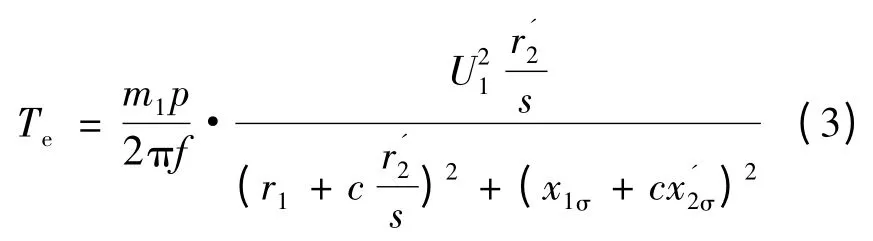
式中:m1、p、f 分别为定子绕组的相数、极对数、频率。
根据调速的需要,变频调速异步电动机可能运行在低频段,此时的计算参数与高频段有很大不同,其定子绕组漏抗不再远大于定子绕组电阻,因此按式(2)、式(3)计算电磁转矩可能偏离实际。但若采用图3 的准确Г 型等效电路模型计算,又会引入复数性质的校正系数,给计算带来不便。为了避免复数校正系数的计算,同时考虑到定转子电阻的影响,本文提出一个新的校正系数计算方法:
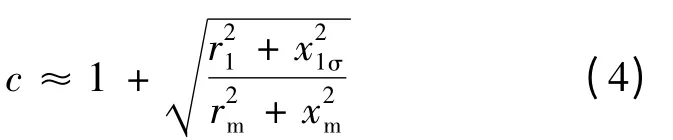
在利用通用π 型等效电路进行异步电动机电磁转矩计算中,要进行三重循环迭代。最里一层以磁路计算为循环判据,中间一层以转差率s 为迭代量,以输出功率为循环判据,最外一层以电动势计算为循环判据(参见图5)。在迭代过程中,π 型等效电路中的磁化电抗xμ随磁路饱和程度变化、铁耗电阻rFe随磁密大小变化,定转子漏抗随饱和系数变化,其算法十分复杂[3-4],如果处理不当,有可能出现迭代震荡或不收敛现象。
为了简化计算,对于采用恒磁通控制的变频调速异步电动机,气隙磁链不变,根据图2 的π 型等效电路模型,在转子侧可利用气隙磁链来直接计算电磁转矩[6]:
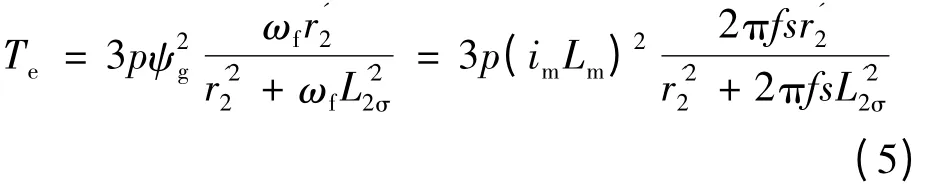
式中:ψg为气隙磁链;ωf为转差角频率;L′2σ为转子绕组漏感的归算值;im为激磁电流;Lm为激磁电感。
在气隙磁链不变的情况下,磁路的饱和程度不变,式(5)中转子电阻、转子漏感、激磁电流、激磁电感等大部分物理量近似为常数,只需计算一次,计算简单、快捷,其计算量比通用π 型等效电路模型大为减少。本文称之为恒磁通π 型等效电路计算模型。
综上所述,根据不同情况,变频调速异步电动机电磁转矩的计算方法可归纳为四种模型,如表1 所示。

表1 四种等效电路计算模型
1.2 电磁设计程序
为了验证上述各种计算模型的适用情况,首先根据三相异步电动机的电磁设计程序,求出电阻和电抗参数,然后分别代入四种等效电路计算模型中,算出各自对应的电磁转矩,最后与通用π 型等效电路计算模型的结果对比。若相符合,则说明该计算模型可用;若不同,则说明该计算模型有局限性。
为了计算变频调速电动机的电磁转矩,应首先给定每个校核点的供电电压、转子转速(或定子频率)、输出转矩。其基本计算思路为先假设电动势E,再假设转差率s,然后计算该转差率下的电阻、电抗值,其次计算出电磁功率,进而求出电磁转矩Te。与给定转矩对比,若不同,则重新假设s;若相同,则继续计算此时的电压U1。若计算电压与给定电压不同,则重新假设E;若相同,则迭代结束,输出此时的转差率。其计算流程如图5 所示。
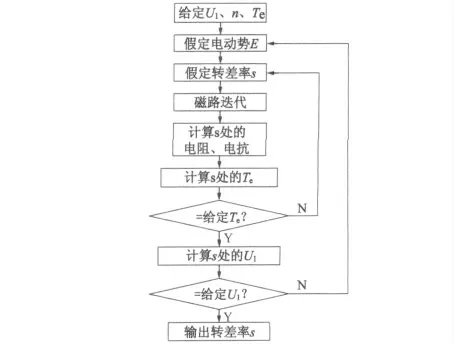
图5 通用π 型等效电路计算流程图
对于采用恒磁通调速的变频电动机,已知供电频率便可直接求出对应的E,不再需要假设E,而只需要假设s。因此,采用恒磁通π 型等效电路计算模型,可减少不必要的迭代,提高计算速度。
1.3 计算实例
对某额定功率为2.2 kW、额定电压为380 V、额定频率为50 Hz、Y 接、6 极、恒磁通控制的三相变频调速异步电动机,采用上述四种等效电路计算模型,对以下四种不同运行工况下的电磁转矩分析进行计算。当电机运行在高频轻载时,取U1= 186.5 V、f =45.2 Hz、s = 0.005,得到的计算结果如表2 所示;当电机运行在高频重载时,取U1= 336.9 V、f = 62.8 Hz、s = 0.282 7(此时电机已超负荷运行,电压和频率已超过额定值),得到的计算结果如表3 所示;当电机运行在低频轻载时,取U1= 6.8 V、f = 1.3 Hz、s= 0.272 8,得到的计算结果如表4 所示;当电机运行在低频重载时,取U1= 24.9 V、f = 4.3 Hz、s =0. 786 9,得到的计算结果如表5 所示。由于通用π型等效电路为精确模型,因此其它的计算结果均以通用π 型等效电路模型的计算结果作为误差分析的参考。
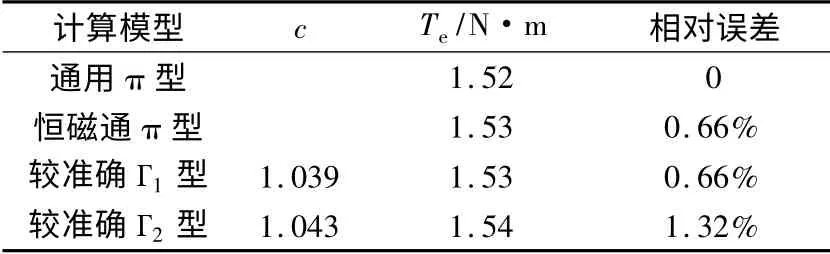
表2 高频轻载运行工况
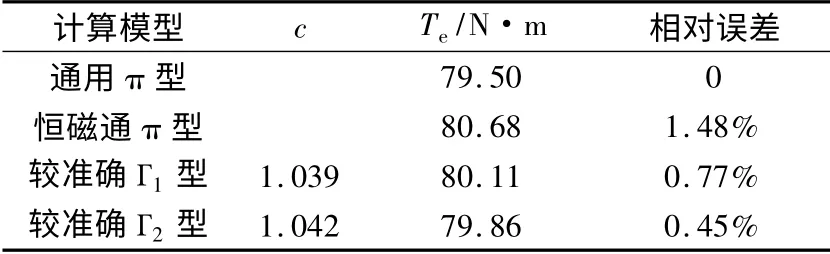
表3 高频重载运行工况

表4 低频轻载运行工况
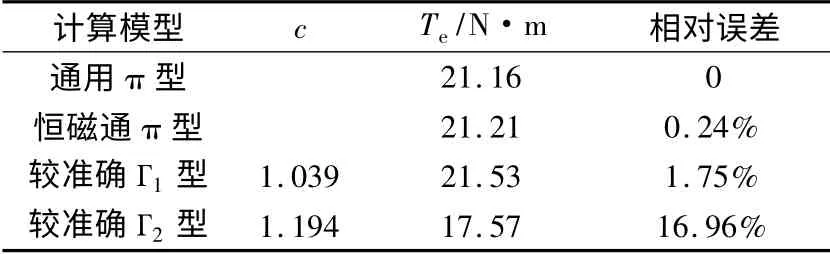
表5 低频重载运行工况
由表2~表5 可见,在高频段,采用四种不同的等效电路计算模型,得到的电磁转矩误差均很小,其中较准确Г1型和Г2型等效电路计算模型没有明显的差别。为了简化算法、提高计算速度,建议采用较准确Г1型等效电路模型。然而,在低频段,较准确Г1型和Г2型等效电路计算模型均出现较大计算误差。同时可见,在四种不同运行工况下,恒磁通π型等效电路计算模型的误差都很小,完全满足工程设计的要求。对于恒磁通控制的变频调速异步电动机,建议采用恒磁通π 型等效电路计算模型,以达到减少计算量、提高计算速度的目的。而对于低频调速过程中气隙磁链发生变化的情况,则必须采用通用π 型等效电路计算模型。
以上结论同样适用于变频调速异步电动机最大转矩的计算。
1.4 误差分析
为了深入探讨较准确Г1等效电路模型的计算误差,下面从理论上做进一步分析。式(1)与式(2)之差反映了较准确Г1型等效电路模型的计算误差大小:
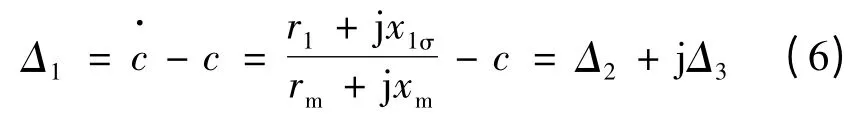
其中:
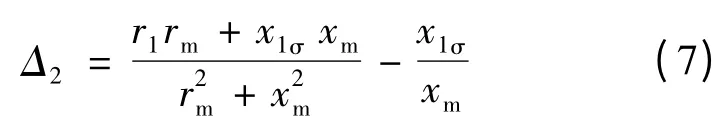
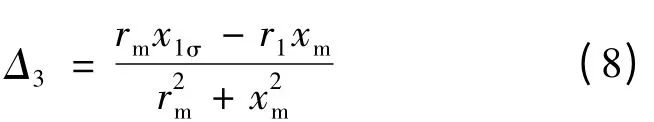
当变频调速异步电动机运行在高频段时,由于频率较高,x1σ>>r1,xm>>rm,则式(7)可化简为:
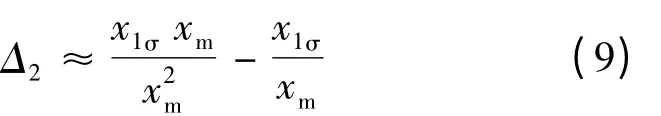
此时,很容易得到Δ2≈0,同理可推出Δ3≈0,进而推出Δ1≈0,因此在高频段较准确Г1型等效电路模型的计算误差很小。上述算例的计算数据验证了理论分析的结果。
当变频调速异步电动机运行在低频段时,在电压和频率不变的情况下,电机的负荷从轻载到重载过程中,随着定子电流的增大,定子绕组漏阻抗压降增大,电动势降低,主磁通减少,铁心的饱和程度降低,因此rm和xm增大,x1σ略有增大,r1不变(忽略温度的影响)。由式(8)可见,Δ3中分母为rm和xm的平方和,变化最大,因此随着负载的增加,铁心的饱和程度降低,Δ3将减小。
对式(7)做进一步推导,可得:
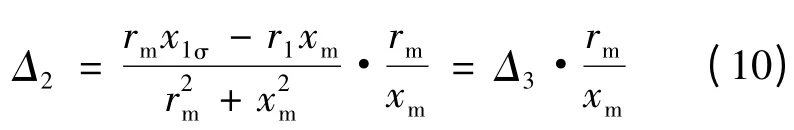
由式(10)可见,随着负载的增加,铁心的饱和程度降低,由于rm和xm同时增大,因此近似不变。当Δ3减小时,Δ2随之减小。再由式(6)可知,Δ1也随之减小。因此,对于较准确Г1型等效电路计算模型,低频重载时误差较小,而低频轻载时误差最大,与计算实例相符。
同理,可对较准确Г2型等效电路计算模型进行误差分析,在此不赘。
2 最大转矩计算
为了区分变频调速异步电动机在高频运行段和低频运行段的不同情况,下面分别讨论其最大转矩的具体计算方法。
2.1 高频段
对于变频调速异步电动机,常常需要对成百上千个运行点进行校核计算。如果每个运行点都根据π 型等效电路计算模型的三重循环迭代来寻找最大转矩,则计算速度将十分缓慢。
文献[7]提出假定s,采用通用π 型等效电路模型,考虑集肤效应、漏磁路饱和的影响,计算s 点对应的电阻和漏抗值,进而计算该点的电磁转矩,通过不断比较得到最大转矩。为了提高计算速度,文献[7]采用了0.618 法。然而,在实际编程计算中发现,对于临界转差率较小的电机,采用该方法会出现无法准确找到最大转矩的现象。若要保证计算的可靠性,可采取s 从0~1 逐点试探的方法,但该方法需要搜寻整个变频运行区间,计算量很大,计算速度很慢。
而较准确的Γ1型等效电路计算模型最为简单,可一步求出最大转矩。根据较准确Г1型等效电路,经推导可得到最大转矩以及出现最大转矩时对应的临界转差率[5]:
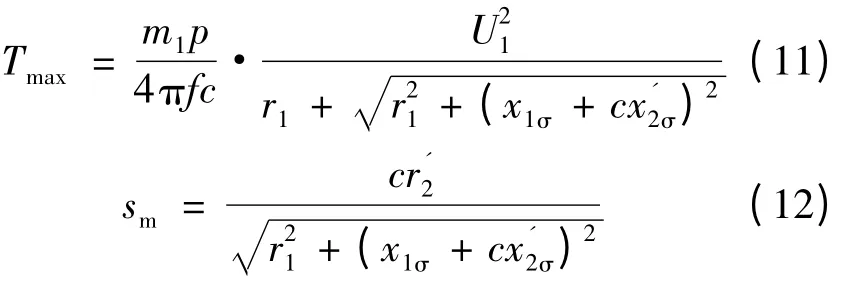
在式(11)、式(12)中,各参数均默认为额定工况下的值。而在最大转矩点,定转子电流达到额定电流2~3 倍,电流的增加将引起磁路饱和程度的变化,从而使得定转子漏抗发生变化。因此,如果直接引用额定点的参数计算最大转矩,显然是不合理的。
为了解决上述问题,本文提出一种新的计算方法。以0.4 倍当前点电压作为供电电压,对电动机进行堵转参数的计算,此时的电流大约为额定值的2~3 倍,其电阻和漏抗参数接近于最大转矩点的情况。将计算出的电阻和漏抗参数代入较准确Г1型等效电路模型,并利用式(11)计算就可得到最大转矩。本文将这种修正参数后再计算最大转矩的方法称为较准确Г3型等效电路模型。
对上面提到的三相异步电动机,采用通用π型、较准确Г1型及本文提出的较准确Г3 型等效电路计算模型,分别对最大转矩进行计算,其结果如表6 所示。由此可见,在高频段,较准确Г1型、Г3型等效电路计算模型的误差不大,但其计算效率远高于通用π 型等效电路模型。

表6 三种等效电路计算模型最大转矩对比(2.5 kW)
为了进一步分析较准确Г1型、Г3型等效电路计算模型对最大转矩的计算精度,下面对另一台大容量的三相异步电动机最大转矩进行计算,其基本参数:额定功率1.2 MW,额定电压1 400 V,额定频率60 Hz,Y 接,4 极。计算结果如表7 所示。
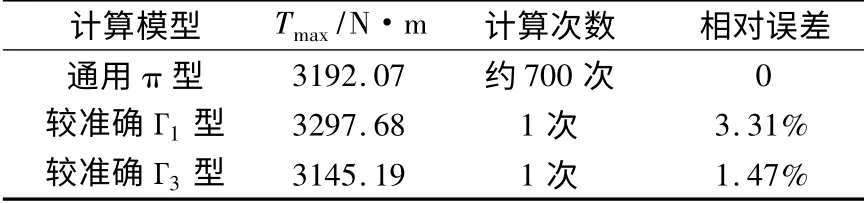
表7 三种等效电路计算模型最大转矩对比(1.2 MW)
对比表6 和表7 的最大转矩计算精度可见,较准确Г1型等效电路计算模型更适合小容量的电机,而较准确Г3 型等效电路计算模型更适合大容量的电机。究其原因,小电机的定子电阻比重较大,使得堵转时定子漏阻抗电压降占外施电压的比例过大,对主磁路的饱和程度影响太大,影响较准确Г3型等效电路的计算精度。因此,本文推荐在sm≤0.1 时采用较准确Г3型等效电路模型来计算最大转矩比较合适,否则还是采用π 型等效电路模型。
2.2 低频段
在低频段,较准确Г1型和Г3型等效电路计算模型都不再适合最大转矩的计算,而只能根据π 型等效电路模型,通过转差率逐点试探法来寻找最大转矩。逐点试探法可靠性高,但计算速度很慢。为了简化最大转矩的计算,许多文献认为,在式(5)中令即可求得使电磁转矩达到最大值时的临界转差率:

然后,把式(13)代入式(5),就可求出最大转矩。然而,这种方法只是一种数学上的推导。实际上,即使对于恒磁通控制的变频调速异步电动机,ψg和L′2σ也随s 的变化而变化,因而不能简单处理。
为了准确而快速地计算低频段的最大转矩,根据通用π 型等效电路计算模型,本文采用转差率定步长试探法。该方法的基本思路:在最大转矩出现的sN~sm区间,转矩-转差率曲线为单调函数。此时,可从额定转差率sN开始迭代,首先令s1= sN,然后每次增加固定步长Δs:

将s1、s2代入π 型等效电路模型,计算出对应的电阻和漏抗参数,进而计算出对应的电磁转矩Te1和Te2。若Te2>Te1,则令s1= s2、Te1= Te2,并重复上述迭代过程;若Te1>Te2,则此时的Te1便为最大转矩Tmax、对应的转差率s1就是临界转差率sm。该算法的流程如图6 所示。
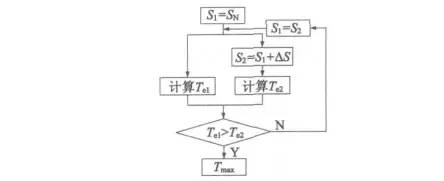
图6 转差率定步长试探法求最大转矩流程图
由于sN和sm一般相差不大,因此该方法计算快捷,不会出现迭代震荡或不收敛等现象,计算速度和可靠性显著提高。
3 结 论
(1)通用π 型等效电路反映了异步电动机内部电磁关系的物理本质,是一种精确模型,适用于变频调速异步电动机各种工况下电磁转矩和最大转矩的计算。但其算法复杂,计算速度慢,有时甚至会出现迭代震荡现象。
(2)对于恒磁通控制的变频调速异步电动机,建议采用恒磁通π 型等效电路模型来计算电磁转矩,在保证计算精度的前提下可有效减少计算量,在计算点数较多的情况下可明显提高计算速度。
(3)变频调速异步电动机在高频运行工况下,建议采用较准确Г1型等效电路模型来计算电磁转矩,这是最简单、快捷的算法,其计算精度能够满足工程设计的需要。但不能采用该模型来计算低频运行工况下的电磁转矩。
(4)本文提出的较准确Г3型等效电路计算模型,计算速度快、精度高,适合于变频调速异步电动机最大转矩的计算,但要求临界转差率不宜过大。
(5)根据π 型等效电路,本文提出的转差率定步长试探法,适合于变频调速异步电动机低频运行工况下最大转矩的计算。
[1] 上海电器科学研究所.中小型三相异步电动机电磁设计程序[M].上海:上海电器科学研究所,1971.
[2] 李伟,韩力.感应电动机变频运行的方式及特性[J].防爆电机,2003(4):4-7.
[3] 陈伟华,黄国治.基于精确等效电路的异步电机第二版电磁计算程序[J].中小型电机,1992,19(1):2-6,23.
[4] 王亚峰,韩力,谭春雨.基于π 型精确等效电路的三相异步电动机电磁设计程序改进及其探讨[J].电机技术,2003(2):3 -5.
[5] 许实章.电机学(下册)[M].北京:机械工业出版社,1988.
[6] 王成元,夏加宽,孙宜标.现代电机控制技术[M].北京:机械出版社,2008.
[7] 陈伟华,黄国治,罗应立.电磁计算程序(第二版)的最大转矩、起动性能计算[J].中小型电机,1992,19(6):6-10.
