基于多尺度联合仿真的汽车加速踏板强度分析
2021-09-29唐俊琦吴奕东孙涛余家皓李明赵勇
唐俊琦,吴奕东,孙涛,余家皓,李明,赵勇
(广州汽车集团股份有限公司汽车工程研究院,广东广州 511434)
0 引言
加速踏板是汽车中非常重要的零部件,它控制着汽车动力的输出,如果其在驾驶中发生断裂可能会导致严重的安全事故,所以保证加速踏板具有一定的强度是非常重要的,而仿真分析可以指导加速踏板强度性能设计,且可以缩短开发周期,有效地节约成本。
目前乘用车使用较多的为悬挂式的加速踏板,其材料主要为玻纤增强型复合材料。相比于传统金属材料,玻纤增强型复合材料具有比强度、比模量高的优点,目前广泛应用于汽车、航空、机械等领域。玻纤增强型复合材料具有明显宏观各向异性的属性,而传统的仿真分析是采用各向同性材料本构对零部件进行有限元分析[1],这种方法主要用于金属材料零部件的强度分析中[2-3],但该种方法不能够精确分析玻纤增强型复合材料零部件的易破坏位置及极限承载力。目前,张玉丽等[4-5]对于玻纤增强型复合材料注塑成型零件采用复合材料建模、模流分析、结构分析的多尺度联合仿真方法进行结构性能分析,最后结果采用Mises应力或者应变来评价,但玻纤增强型复合材料的纤维取向不同,其各个方向的强度性能是不同的,无法用一个固定的应力或应变值作为评价标准,这时就需要引入复合材料强度理论。
工程中常用的复合材料强度失效准则有蔡-希尔准则和蔡-吴准则。这两种失效准则都是基于Mises屈服失效准则推导而来。近些年,多位学者基于这两种失效准则,对使用复合材料的零部件进行强度分析。徐鹍鹏等[6]基于蔡-希尔失效准则对应变强化型移动式真空绝热容器进行强度分析;卢志强等[7]基于蔡-吴失效准则对TSCB人行桥进行了强度分析,但他们都没有结合容器的模流信息,而使用了理想的各向异性本构模型。
本文作者采用结合复合材料建模、模流分析、结构强度分析的联合仿真分析方法对某车型加速踏板进行分析,同时采用基于蔡-希尔和蔡-吴失效准则的失效因子进行评价,并探讨不同失效准则对结果评价的合理性,验证了联合仿真分析方法在加速踏板强度分析的可行性。
1 加速踏板台架试验
1.1 边界条件及载荷工况
试验前需要将加速踏板总成固定在夹具上,来模拟实际安装在整车上的效果。
加速踏板主要的使用工况为沿踏板面正向踩踏,所以文中按照此工况对加速踏板进行台架试验,加载示意图如图1所示,加载方法可描述为:加速踏板在全行程位置,过加速踏板面中心沿法向方向施加正向载荷直至加速踏板开裂。

图1 加速踏板加载示意
1.2 台架试验
台架试验设备采用INSTRON 5966电子万能试验机。对加速踏板按照第1.1节中所述的工况加载直至加速踏板开裂,如图2所示,试验加载速度为30 mm/min。

图2 加速踏板加载情况
选择同一批次3个加速踏板样件进行台架试验,得到力-位移曲线如图3所示。可发现在加载过程中,曲线中有力突然减小的波动,这是因为此时踏板臂已有地方先开裂但整体还未完全断裂,之后踏板臂还可以继续承载,直至踏板臂断裂。
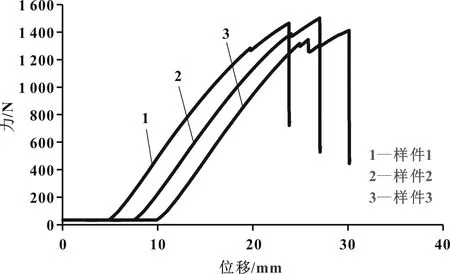
图3 台架试验力-位移曲线
根据实际台架试验及力-位移曲线图,得到该车型加速踏板初始开裂时及最终断裂时的承载力,如表1所示。

表1 极限承载力试验结果
2 加速踏板仿真方法
2.1 有限元模型建立
在HyperMesh软件中创建加速踏板模拟台架试验的有限元模型,其中单元基础尺寸为1 mm,采用四面体单元建模,螺栓、转轴和液压缸加载位置采用刚性单元连接,转轴处释放转动方向自由度,加速踏板与夹具连接位置约束其六向自由度,分析工况与台架试验一致。网格模型如图4所示。

图4 加速踏板网格模型
2.2 多尺度联合仿真
为表现玻纤增强型材料各向异性的属性,采用多尺度耦合的联合仿真分析方法。除建立有限元分析模型外,还需要使用Digimat软件建立玻纤增强型复合材料微观结构初始模型,包括定义玻纤及基体的密度、弹性模量、泊松比、屈服强度、硬化模量、硬化指数、硬化线性模量等材料参数,以及玻纤质量分数、玻纤长宽比、玻纤取向张量等微观结构参数。
然后,通过逆向工程修正实际材料应力应变曲线与初始材料模型间的偏差。同时,使用Moldflow软件进行模流分析,模拟材料在注塑过程中的流动,获得加速踏板玻纤取向信息并映射到结构模型中。
最后,将映射后的纤维取向信息、材料信息、有限元模型提交至Abaqus求解器中进行耦合计算。联合仿真分析流程如图5所示。

图5 联合仿真分析流程
3 结果分析
3.1 蔡-希尔与蔡-吴失效准则数学模型
蔡-希尔与蔡-吴失效准则中用失效方程定义结构的失效,当失效方程F(ε)=1时正处于结构失效的临界点。Digimat中定义了失效因子f使F(ε/f)=1,当失效因子f=1 时,表示当前结构处于失效面上,即为F(ε)=1时,而此时模型的受力即为极限承载力。失效准则中输入的参数,是通过材料样条测试试验获得,而样条在横截面上是各向同性,在纵截面上是各向异性的,即表现为横观各向同性。所以两种失效准则也采用横观各向同性的数学模型。
蔡-希尔失效准则横观各向同性数学模型可以表示为(1轴方向的横截面为各向同性):
(1)
其中,
(2)
式中:f为失效因子,ε11、ε22、ε33、ε12、ε13是复合材料在各方向的应变分量,X为最大轴向拉伸应变,Y为最大横向拉伸应变,S为最大面内剪切应变。
蔡-吴失效准则横观各向同性经验数学模型可以表示为(1轴方向的横截面为各向同性):
F(ε/f)=1
(3)
其中,
(4)
式中:Xt为最大轴向拉伸应变,Xc为最大轴向压缩应变,Yt为最大横向拉伸应变,Yc为最大横向压缩应变。
3.2 仿真与试验结果对比
3.2.1 极限承载力结果对比
在仿真过程中,当某个单元失效因子达到1时认为此单元已经发生破坏,但在之后的分析中此单元仍然继续存在,所以在某单元失效后的分析结果是与实际情况不符的,所以只关注最先开裂的位置,其中表2中的极限承载力也是根据最先开裂位置计算出来的,同时也与试验中最先开裂位置的承载力相对应。

表2 极限承载力仿真结果
对比两种失效准则极限承载力的仿真值如表2所示,可知采用蔡-吴失效准则计算的极限承载力大于采用蔡-希尔失效准则计算的极限承载力。分析原因为:纤维增强型复合材料在材料的主方向的拉压强度通常是不同的,而其中横向拉压强度差别更大,但蔡-希尔失效准则认为复合材料的拉压性能是相同,而蔡-吴失效准则是可以表示拉压性能的差异。玻纤增强型复合材料的抗压性能优于抗拉性能的,所以使用蔡-希尔失效准则计算的失效因子会偏大,因此极限承载力仿真结果会偏小。
将极限承载力仿真结果与表1中的试验结果做对比,可发现蔡-吴失效准则计算的结果更加接近试验结果,其仿真值与试验值的相对误差在10%的范围以内,可见采用蔡-吴失效准则计算的极限承载力较为精确。
3.2.2 开裂位置对比
如图6所示,对比不同失效准则下的仿真模型的最先开裂位置,可发现两个计算结果显示的最先开裂位置不同,但两个位置的失效因子都较大,表示这两个位置都是受力较大的位置。将仿真结果与图7中台架试验结果对比,可发现采用蔡-吴失效准则的模型所表示的最先开裂位置更接近台架试验结果,再次验证采用蔡-吴失效准则计算更加符合实际情况。
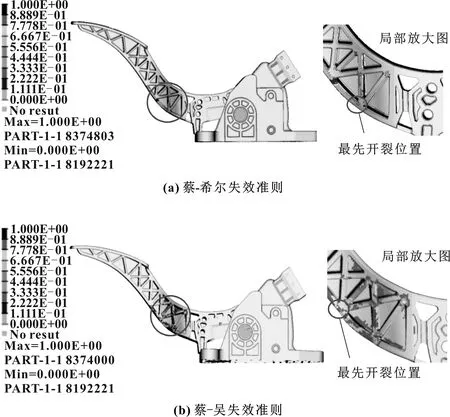
图6 不同失效准则下仿真模型破坏位置

图7 加速踏板台架试验破坏位置
4 结论
通过研究多尺度联合仿真方法进行加速踏板强度分析,主要得出结论如下:
(1)加速踏板使用材料通常为玻纤增强型复合材料,而复合材料其各向异性的属性,导致加速踏板不能再用传统金属的各向同性材料本构进行强度分析,需要采用适用于复合材料的失效准则进行分析,如蔡-希尔或蔡-吴等失效准则。
(2)文中分别采用蔡-希尔和蔡-吴失效准则计算加速踏板的极限承载力。从仿真结果与试验结果对比中可以看出,使用蔡-吴失效准则仿真计算得到的极限承载力数值以及最先开裂位置都与试验结果相接近,且极限承载力的相对误差在10%范围内,所以蔡-吴失效准则更适用在玻纤增强型复合材料的强度仿真中。
