基于气门弹簧设计关键参数的计算与校核

孙辉国，韦静思，吕伟，梁明曦，占文锋

(广州汽车集团股份有限公司汽车工程研究院，广东广州 511434)

0 引言

气门弹簧是发动机配气机构最重要的零部件之一，是保证气门及整个配气机构能够平稳运行的关键零部件。在凸轮运行在基圆部分时，保证气门与气门座圈密封紧闭，不发生二次开启；在凸轮运行在开启部分时，确保凸轮与从动件之间不发生脱离；在气门落座瞬间，保证气门不发生过大冲击。因此气门弹簧力不宜过小也不宜过大，所以气门弹簧关键参数的选择对发动机配气平稳运行是至关重要的[1-2]。

本文作者通过大量的经验和总结，明确了气门弹簧关键参数(F1、F2和工作段平均刚度k)的计算公式及流程。基于广汽某款发动机气门弹簧的选型，在设计早期正向确定能够满足配气机构稳定运行的气门弹簧。并通过配气机构运动学与动力学分析，证明文中提到的气门弹簧选型的方法和流程简便高效，值得推广。

1 气门弹簧相关参数的确定

1.1 气门弹簧预紧力F1的计算

当气门动作在凸轮基圆阶段时，此时气门是关闭的。气缸内的气体压力较大，对气门密封有利，但是如果气道内气体压力大于气缸内的气体压力，气门两边的压力差会使关闭的气门打开，即在发动机压缩和膨胀行程时出现气门关不严的情况。为了避免这样的情况发生，气门弹簧残余力(Frs)应该满足以下要求：

Frs=F1×0.85-Fa-Fb-Fc-Fd>30 N

(1)

式中：Frs为气门弹簧残余力，N；

Fa为气门两侧气体的压力差，N；

Fb为气道压力循环波动的力，N；

Fc为气门受液压挺柱的顶开力，N；

Fd为气门反弹时约10g的惯性力，N；

F1×0.85为考虑弹簧的公差以及颤振,取F1的85%。

(1)Fa为气门两侧气体的压力差[3]，计算公式为

(2)

式中：pp为气道压力，MPa；

pc为缸内压力，MPa；

Dv为气门密封面直径，mm；

Ds为气门杆直径，mm。

(2)Fb为考虑气道压力循环波动对气门压力的影响，其中气道压力波动值Δp=0.05～0.1 MPa，计算公式为：

(3)

(3)Fc为气门受液压挺柱内油压的顶开力，计算公式为

Fc=Fhlif·Lcam/Lvalve

(4)

式中：Fhlif为油压对挺柱柱塞的推力，N；

Lcam为凸轮侧摇臂力臂长度，mm；

Lvalve为气门侧摇臂力臂长度，mm。

(4)Fd为气门反弹时阀面受到的约10g的惯性力，计算公式为

Fd=10×9.8×M

(5)

式中:M为阀系的运动总质量，其计算公式为

(6)

式中：mv为气门质量，kg；

mc为气门上座质量，kg；

ml为气门锁片质量，kg；

ms为气门弹簧质量，kg；

If为摇臂转动惯量，kg·m2；

Lf为摇臂支撑点到气门中心线的距离，m。

按照以上公式分别确定Fa、Fb、Fc和Fd，由Frs>30 N可以得到F1的理论最小值,这个理论最小值可以确保凸轮运行在基圆部分时，气门与气门座圈密封紧闭，不发生二次开启。

1.2 气门最大升程弹簧力F2的计算

一般当气门升程最大时，负加速度绝对值最大，此时气门弹簧力F2需要克服阀系运动质量的惯性力，避免出现摇臂滚子与凸轮飞脱的情况，同时考虑一定量的弹簧安全系数t=1.1～1.8，即气门最大升程弹簧力F2的公式为：

F2>M·a·t

(7)

式中：t为弹簧安全系数；

a为气门最大负加速度绝对值，m/s2，如图1所示。

图1 气门加速度曲线

1.3 气门弹簧工作段平均刚度k的计算

公式(1)和(7)确定了气门弹簧的F1和F2，则气门弹簧工作段的平均刚度k的计算公式为

k=(F1-F2)/Sh

(8)

式中：Sh为气门开启最大升程，mm。

1.4 对于F1不宜过小的补充说明

如果F1过小，则会使气门弹簧工作段的平均刚度太大，导致弹簧设计困难。同时F1过小，在气门开启初期，弹簧力过小无法克服气门的惯性力，导致凸轮与从动件发生飞脱现象。

2 气门弹簧的选型计算

文中基于广汽某款机型运用以上计算公式进行气门弹簧的选型计算。以验证公式使用的可行性。表1为计算需要输入的数据。

表1 气门弹簧选型计算输入

根据公式(1)，可以得到F1>150 N;根据公式(7)，可以得到F2>440 N;根据公式(8)，可以得到气门弹簧工作段平均刚度k=30.7 N/mm。气门弹簧供应商按照F1和F2的要求，提供气门弹簧成品。弹簧的具体参数为：F1=260 N，F2=488 N，工作段平均刚度k=46 N/mm。

3 气门弹簧校核计算流程

图2为气门弹簧校核计算的流程，按照计算流程，通过以上公式可以一次确定配气机构需要的气门弹簧关键参数F1、F2和工作段平均刚度k，弹簧供应商按照要求的弹簧参数设计气门弹簧。这样大大减少了仿真和设计来回校核的工作量，提高了工作效率。

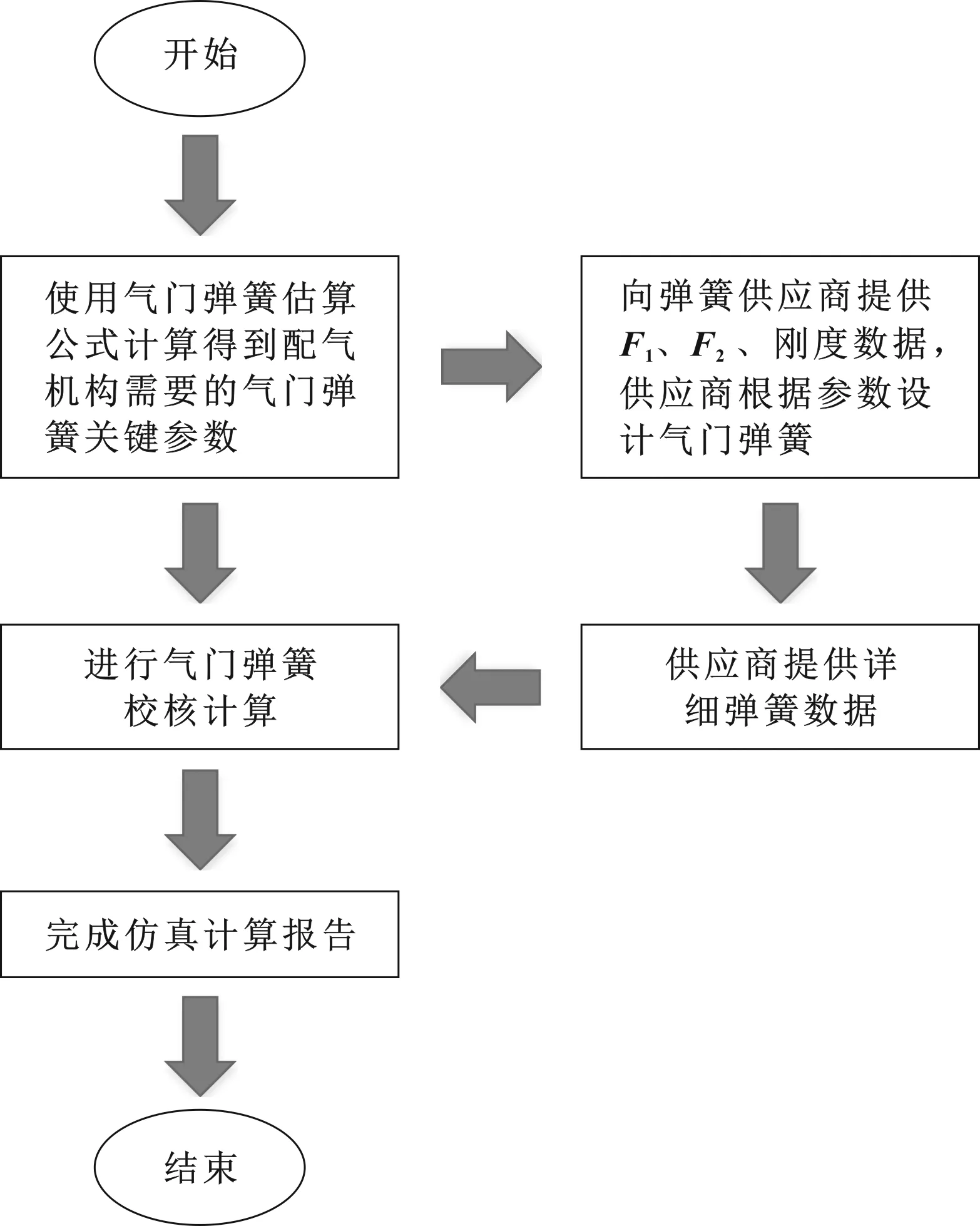
图2 气门弹簧校核计算流程

4 气门弹簧校核计算

气门弹簧对于配气机构至关重要，对于整个配气机构的运动学和动力学结果都将产生较大的影响。因此需要对气门弹簧做更加详细的运动学和动力学分析，以考察气门弹簧是否满足整个配气机构的要求[4]。该发动机配气机构为典型的指型摇臂结构。文中应用AVL-EXCITE软件来进行配气机构的运动学和动力学分析，分析气门弹簧是否能满足配气机构的仿真评价标准。通过AVL-EXCITE软件建立的单阀系分析模型如图3所示。

图3 AVL-EXCITE建立的单阀系模型

4.1 运动学分析结果

(1)凸轮和从动件是两个具有曲面的弹性体，在传递载荷时，就形成了一个接触的区域，并伴随着产生了接触应力。如果凸轮和从动件之间的接触应力太大，在周期性接触应力的反复作用下，将引起凸轮或者从动件工作表面的较大损坏。从计算结果图4来看，凸轮和从动件的接触应力小于1 100 N/mm2，低于设计要求的最大许用应力[4]。

图4 凸轮与从动件接触应力结果

(2)在配气机构运动学分析中，气门弹簧裕度是气门弹簧力与从动件惯性力的比值。气门弹簧力要保证有一定的余量，否则从动件将从凸轮表面跳开，发生“飞脱”现象。但是也不能太大，否则产生过大的摩擦功，影响发动机的性能。从计算结果图5来看，气门弹簧的安全裕度大于t，配气机构不会发生飞脱现象[2]。

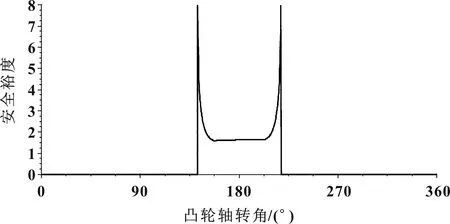
图5 气门弹簧安全裕度

(3)为了防止摇臂在运动中从液压挺柱球头脱落，配气机构要求摇臂对液压挺柱轴向力大于100 N、液压挺柱轴线垂直方向力小于600 N。从计算结果图6来看，液压挺柱轴向和垂直方向的力均满足要求，摇臂不会从液压挺柱球头脱落[5]。

图6 液压挺柱受力结果

(4)由于气门杆头部与摇臂之间是相对滑动的往复周期运动，当两者之间的相对滑动速度过大，同时两者之间的接触应力过大时，则会出现气门杆头部快速磨损的情况。配气机构要求气门杆头部与摇臂相对速度下的接触应力在阈值线以下。从计算结果图7来看，气门杆头部与摇臂之间的相对运动不会引起气门杆的快速磨损[5]。

图7 气门杆头部与摇臂相对速度下接触应力

4.2 动力学分析结果

(1)气门落座的好坏对气门座可靠工作影响很大，当气门落座速度比较大时，会增加气门阀面的磨损，同时产生较大的噪声。图8为气门阀面的运动曲线，从计算结果来看，气门阀面的落座速度小于1 m/s，配气机构不会产生较大的噪声[6]。

图8 气门运动速度

(2)气门关闭时的落座力不应太大，否则会引起气门反跳，导致气门二次开启。通常情况下要求气门阀门落座力小于6倍弹簧预紧力。图9为气门阀面的落座力，从计算结果图来看，气门阀面的落座力小于6倍的弹簧预紧力，气门不会发生反跳现象[6]。

图9 气门阀面受力

(3)图10为凸轮与从动件之间的接触力结果，从计算结果可以看到在凸轮工作段区域，未发生凸轮与从动件之间接触力为0的情况，说明凸轮与从动件未发生飞脱现象[7-8]。

图10 凸轮与从动件接触力

(4)图11为气门弹簧各质量点的受力结果，从计算结果可以看到在凸轮工作段区域，未发生弹簧质量点受力突变的情况，说明弹簧未发生并圈现象。

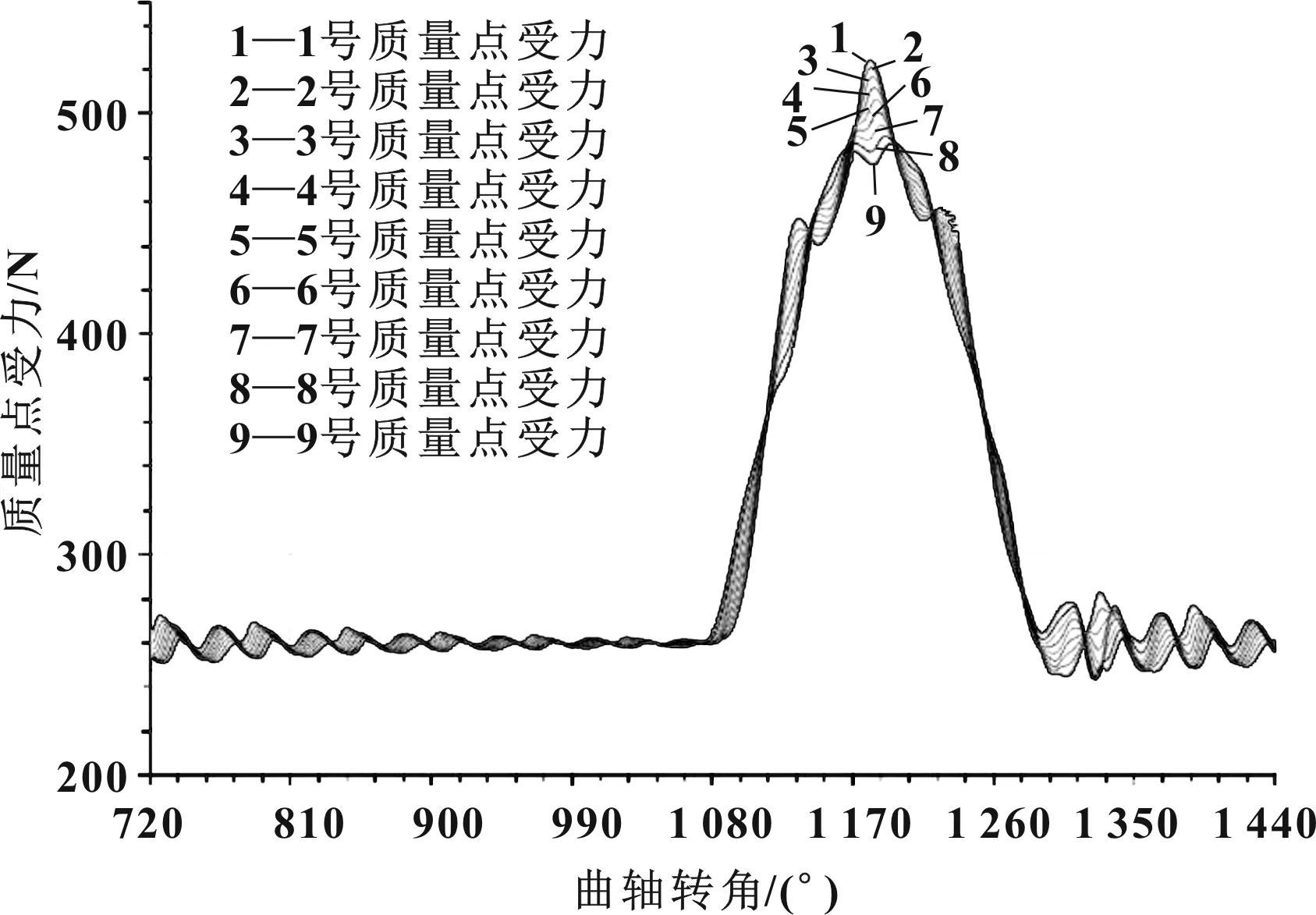
图11 气门弹簧各质量点受力

5 结束语

按照气门弹簧校核计算的流程，通过理论计算以及运动学和动力学的分析，新的气门弹簧符合配气机构仿真的各项评价指标，气门弹簧满足发动机配气机构稳定工作的需要。

通过气门弹簧关键参数的确定，可以在配气机构设计早期，快速地进行气门弹簧的选型，减少了仿真和设计之间来回校核繁琐的工作量，大大地提高了工作效率。文中提出的气门弹簧选型的流程方法简便易行，是一种值得推广的高效的气门弹簧选型方法。