TMD控制高架轨道箱梁结构振动的模型试验研究

2021-09-27张新亚雷晓燕

振动与冲击 2021年16期

张新亚，雷晓燕，罗锟

(1.广州地铁设计研究院股份有限公司，广州 510010；2.华东交通大学铁路环境振动与噪声教育部工程研究中心，南昌 330013)

在高架轨道交通建设中，混凝土箱梁桥的应用较为广泛[1-2]。然而，混凝土桥梁服役过程中的结构振动与噪声已成为制约轨道交通发展的重要因素。混凝土桥梁结构振动会向周围环境辐射噪声，并且噪声以0～200 Hz的较低频段为主，该频段噪声对人的注意力、反应时间及语言辨识能力等有诸多负面影响[3]。振动为噪声之源，因此，找到减少桥梁结构振动的合理措施，对保证轨道沿线的环保健康、促进轨道交通的发展都具有重要意义。

调谐质量阻尼器(tuned mass damper,TMD)不仅可以有效减少结构的动力响应，而且其具有构造简单、安装容易、维护方便的特点，近年已经被广泛成功应用于高层建筑、高耸结构以及大跨桥梁等大型建筑的振动控制[4]。针对轨道桥梁振动与噪声问题，肖新标等[5]研究了TMD对移动荷载作用下桥梁振动的控制规律；王浩等[6]以南京长江大桥为研究对象，研究了TMD在该桥减振控制中的参数敏感性和控制效果。顾萍等[7]分析了多重调谐质量阻尼器(multiple tuned mass dampers,MTMD)抑制铁路钢桁梁桥横向振动的振动效果，也发现相对于TMD，MTMD可扩大减振范围，改善减振系统的鲁棒性；张迅等[8]选取32 m双线混凝土简支箱梁为研究对象，对安装MTMD能否达到减振、降噪的双重效果进行了研究。张新亚等[9]采用有限元的方法研究了TMD控制多阶模态振动的效果，具有一定的实用意义。

但是，可以发现以上研究均停留在理论研究与数值计算上，而TMD在铁路简支箱梁中的试验研究鲜有文献报道。因此，本文以铁路32 m简支箱梁桥为原型，以10 ∶1为几何缩尺比，设计制作了研究结构振动特性的缩尺试验模型，并验证了试验模型的可靠性。在此基础上，通过单点简谐激振，试验研究了TMD控制高架轨道箱梁结构振动的性能。

1 试验模型的设计与制作

1.1 原型简介

某铁路简支箱梁结构，桥长L=32 m，梁宽D=12 m，梁高H=3.05 m，其上部结构为双线CRTS-Ⅱ型板式无砟轨道，结构从上到下依次为钢轨、轨枕、轨道板、CA砂浆层、混凝土底座。梁体采用C50混凝土浇筑，材料弹性模量E=36.2 GPa，密度ρ=2 500 kg/m3。

1.2 模型材料的选取

综合考虑经济、时间成本和试验操作难度，首先确定几何相似常数为CL=10。设计完成的高架轨道箱梁试验模型，如图1所示。梁体、混凝土底座板和轨道板的制作考虑到结构尺寸和操作时长等因素，未选用级配混凝土，而是选用灌浆料浇筑。灌浆料具有流动性好、离析性能差、微膨胀的性能特点，非常适用于小比例混凝土结构物的浇筑。

图1 高架轨道箱梁试验模型Fig.1 Test model of elevated track box girder

钢轨模型按照10 ∶1缩尺比例找厂家选用钢材定制如图2(a)所示。密度为6 870kg/m3，弹性模量为174 GPa，强度满足试验激振要求。通过螺栓紧固件将钢轨固定在轨枕台上，其中钢垫片模拟扣件，如图2(b)所示。CA砂浆层为连接轨道板和混凝土底座的连接层结构，厚度较薄，用灌浆料浇筑操作难度大，查阅相关文献发现，柔韧性较好的橡胶板能较好模拟CA砂浆层特性，而且橡胶板具有很好的耐压耐老化的特点，选用10 mm厚的橡胶材料，如图3所示。

图2 钢轨缩尺模型Fig.2 Scale model of rail

图3 橡胶板材Fig.3 Rubber board

目前高架桥梁中，使用较多的为板式橡胶支座，由于箱梁模型为缩尺浇筑，尺寸较小，相对于足尺试验，该模型质量较轻。为了保证支座约束能够与原型箱梁的边界条件具有相似性的同时，还能方便制作，本试验仿照板式橡胶支座构造设计制作了缩尺支座模型。其采用上下钢板夹橡胶垫块的形式，钢板用膨胀螺丝固定在桥梁与桥墩上，橡胶垫块放置在钢板的限位卡槽中，如图4所示。

图4 橡胶支座Fig.4 Rubber bearing

1.3 模型试验相似常数

研究桥梁振动响应特性时，缩尺试验模型需要满足表1所示与结构性能相关物理量的相似。在这些相似条件均满足的条件下，将模型试验得到的测试结果乘以相似常数即为原型工况对应的响应。

箱梁的弹性模量、密度和几何尺寸作为控制变量需要首先确定。几何尺寸的相似常数即为10，箱梁的密度、弹性模量通过预先浇筑试块测定，试验测得：E1=30 GPa，ρ1=2 203.7 kg/m3。由此可确定控制量：CL=10，CE1=1.206 7，Cρ1=1.134 5，基于相似第一定理、相似第二定理(π定理)和相似第三定理，利用量纲分析法[10]计算出轨道箱梁结构各个参数的相似比，如表1所示。

表1 模型试验相似常数Tab.1 Similarity constant of model test

1.4 试验模型的校验

采用LMS Test.Lab软件的MIMO FRF Testing模块用于测定试验模型的模态，模态试验方案，如图5所示。主要包括激振，数据采集，信号分析及模态参数识别。拾取了前5阶约束模态频率值，如表2所示。振型如图6所示。

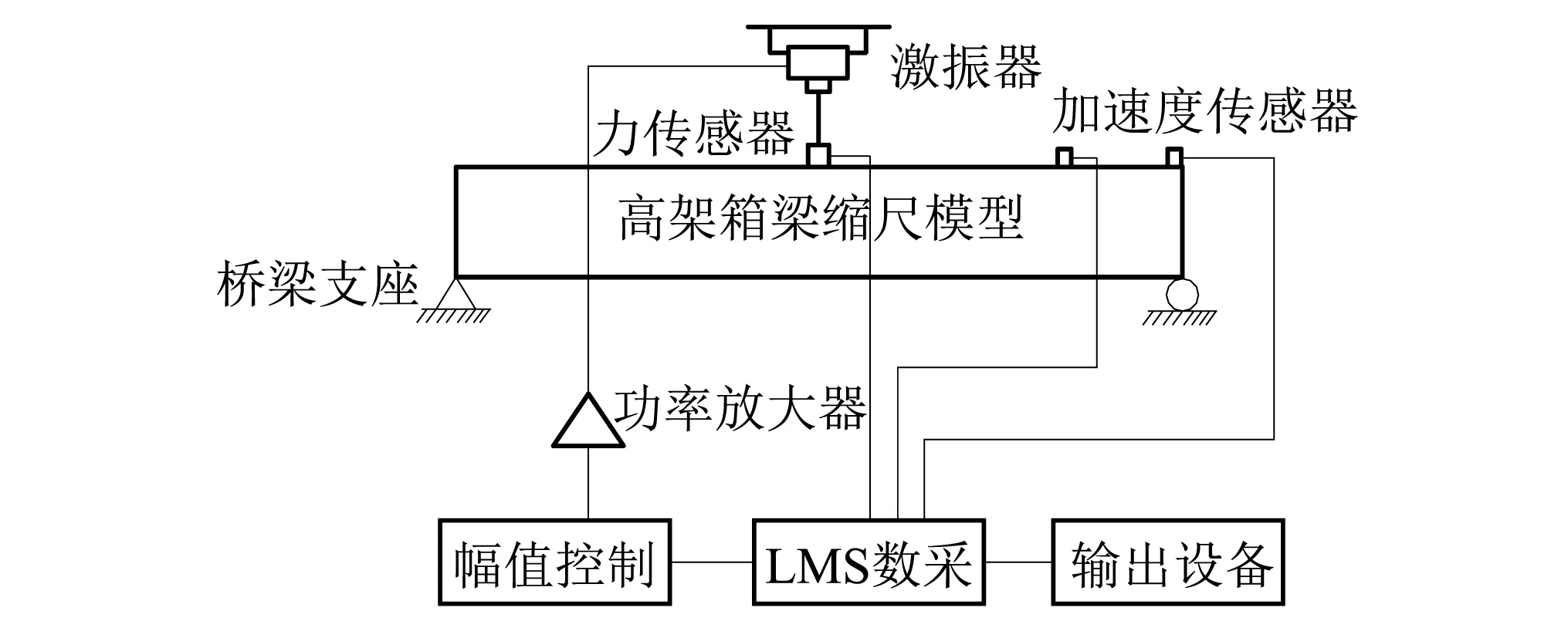
图5 模态测试技术方案Fig.5 Technology solution modal test

同样按照原型桥梁的1/10缩尺定义几何尺寸，适当简化后，利用有限元分析软件ANSYS建立高架轨道箱梁结构动力分析模型，如图7所示。采用Block Lanczos方法进行模型的模态求解，计算了前5阶模态的自由模态频率值与试验结果对比，如表2所示。振型对比如图6所示。

图6 识别的前5阶模态振型对比Fig.6 Comparison of the first 5 modes

图7 轨道箱梁结构有限元模型Fig.7 Finite element model of track box girder structure

由表2和图6计算与试验结果对比可以发现，前5阶模态频率的误差均在10%以内，其中前4阶模态频率误差较小，第5阶模态频率误差略大为6.35%。模态试验得到的前4阶振型与有限元分析结果相比振动趋势基本一致，第5阶振型误差较大。整体来看，试验模型还是具有较高的可靠性，可用于研究轨道箱梁结构的振动响应特性。

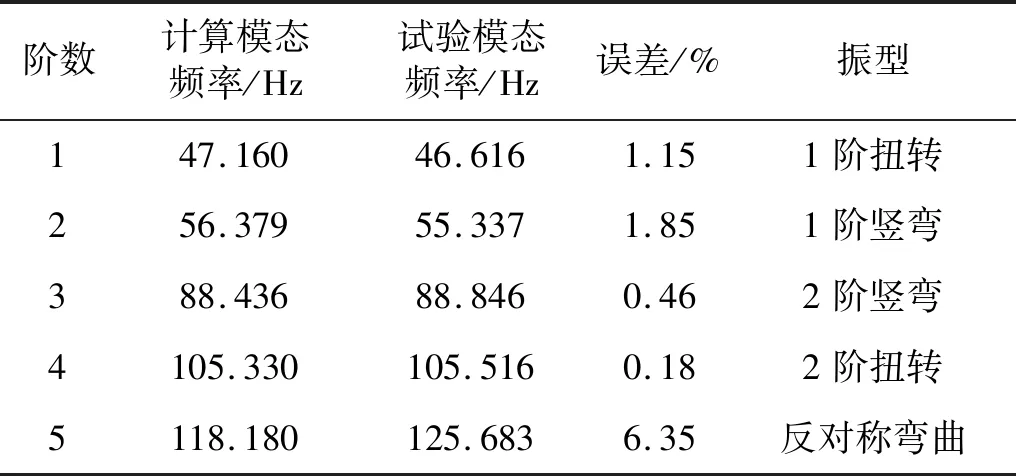
表2 自振频率对比Tab.2 Comparison of natural frequency

2 TMD模型制作及特性测试

2.1 TMD设计理论

混凝土桥梁结构阻尼非常小，在忽略主结构自身阻尼的情况下，TMD存在最优调谐参数[11]。通过在主结构上附加该弹簧阻尼减振系统，原固有频率附近产生的振动响应峰值会产生明显的下降。理论上的TMD最优调谐参数的计算表达式

(1)

(2)

根据已经计算得到的最优频率比ηop和最优阻尼比ζop值，可推导附加调谐质量阻尼器系统的最优阻尼Cop和最优弹簧刚度Kop

Cop=4πηopζopfm

(3)

(4)

式中：μ为TMD系统质量m和主质量M的比值；在桥梁等多自由度结构中；M为受控模态等价质量；f为主结构的自振频率，Hz。

2.2 TMD的设计与制作

本文箱梁振动控制只关注其垂向的动力学响应，并且列车高速过桥时，基频模态对箱梁的振动贡献最大[12]，所以确定轨道箱梁的受控模态为1阶、2阶模态，分别为1阶扭转模态和1阶竖弯模态，受控频率为46.654 Hz，55.542 Hz。

根据TMD设计理论，通过拟定μ可以得到缩尺模型的TMD最优设计参数，现阶段相关研究成果表明，质量比取值在0.5%～2.0%，综合考虑控制效果、经济与结构安全等多种因素，质量比的取值也不宜过大，由此选定1阶TMD系统的质量比为μ=2%；2阶TMD设计μ=1%和μ=2%两种试验工况，即制作两个μ=1%的试验装置。最优设计参数，如表3所示。其中受控模态等价质量通过有限元模态分析获得。

表3 TMD最优设计参数Tab.3 Optimal design parameters of TMD

如图8所示，为制作成型的TMD减振装置，其中质量块选用钢板作为配重，可通过增减薄钢板的数量调谐自振频率，弹簧阻尼材料为碳素钢弹簧，单根弹簧刚度1.86×105N/m。其中1阶TMD成型质量为12.56 kg，质量误差3.6%，6根弹簧总刚度为11.14×105N/m，刚度偏差10.2%；2阶TMD制作成型两个，其中单个质量为5.94 kg，质量误差5.6%，4根弹簧总刚度为7.44×105N/m，刚度偏差10.7%。

图8 TMD装置外观图Fig.8 Appearance of TMD device

2.3 TMD自振参数的测定

TMD制作过程复杂，难免会出现参数误差，为了保证TMD减振控制效果的精度，首先必须对TMD减振装置的自身动力特性进行测定，包括TMD装置的自振频率以及其阻尼比的测定。采用自由衰减振动法[13-14]对TMD减振装置的自振周期进行测试，如图9所示。在钢板上粘贴加速度传感器，给TMD减振装置的质量块一个初始位移，让其做自由衰减振动。拾取1阶、2阶TMD的钢板振动加速度信号分别如图10、图11所示。

图9 TMD自振特性测试Fig.9 Testing of natural vibration characteristics for TMD

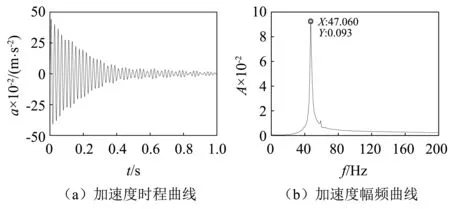
图10 1阶TMD自振特性Fig.10 Natural vibration characteristics of 1st order TMD

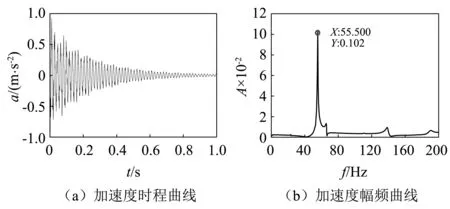
图11 2阶TMD自振特性曲线Fig.11 Natural vibration characteristics of 2nd order TMD

对时域信号作傅里叶变换得到1阶TMD减振装置的自振频率为47.06 Hz，并计算阻尼比为0.019 1，与最优频率相对误差为2.9%，；计算得到2阶TMD减振装置的自振频率为55.5 Hz，阻尼比为0.018 6，与最优频率相对误差为0.93%，总体来看，TMD减振装置的制作满足调谐要求。

3 试验概况

3.1 试验工况与测点布置

为研究TMD减振效果，试验设计了4种工况：工况1为安装TMD前的桥梁模型，工况2为安装1阶TMD(质量比为0.02)的桥梁模型，工况3为安装2阶TMD(质量比为0.01)的桥梁模型，工况4为安装2阶模态TMD(质量比为0.02)的桥梁模型。每种工况分别在振动较大的翼缘板(C1)和腹板(C2)位置布置测点，以分析减振效果。图12为4种工况特征点布置情况。

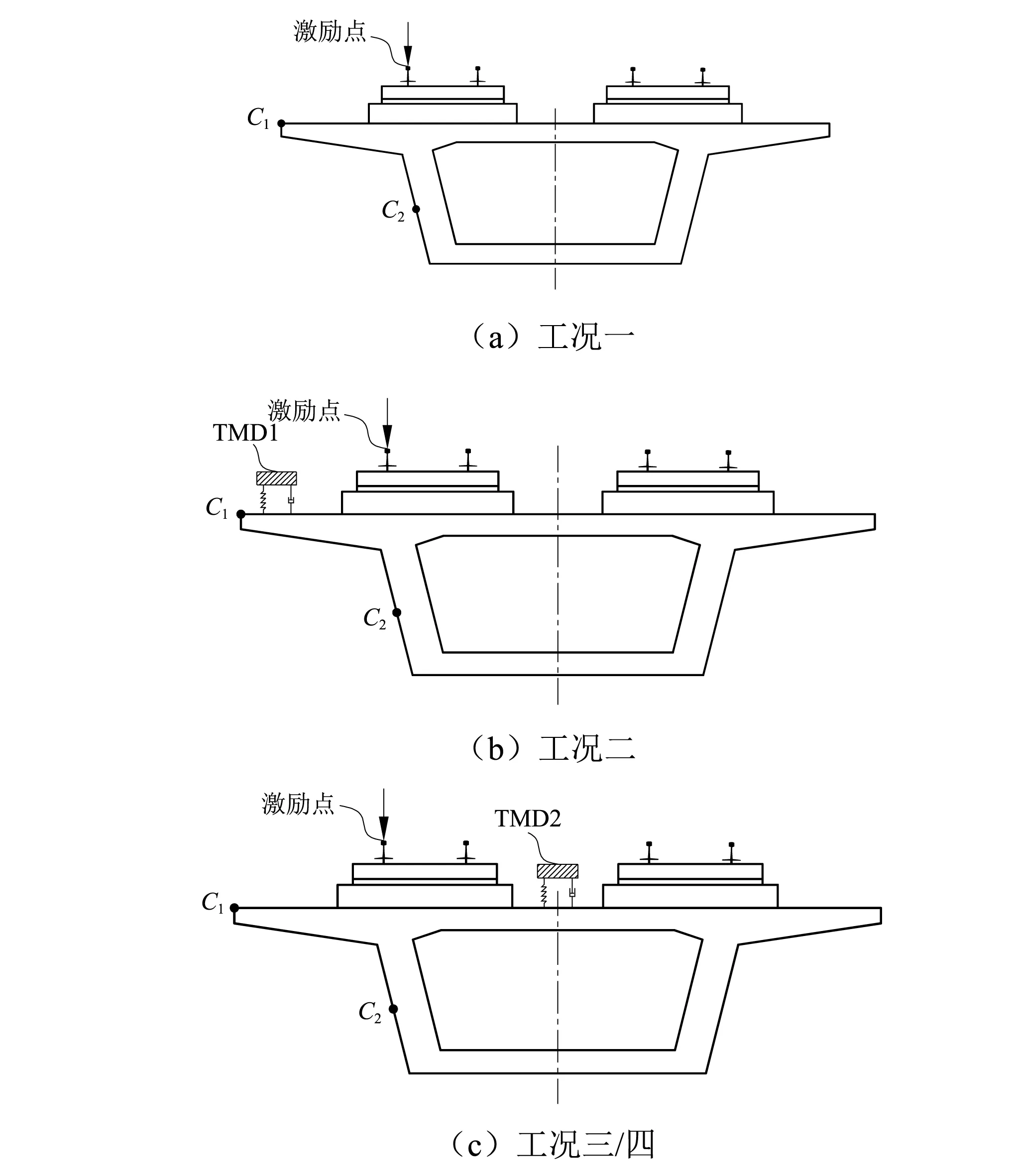
图12 特征点布置Fig.12 Arrangement of feature points

张新亚等的研究指出TMD安装位置应该为受控模态变形最大的位置，即该阶模态的波腹位置，而且安装位置应该为其他模态振动变形较小的点，以减小其他模态的干扰。所以1阶TMD安装在跨中截面翼板位置，2阶TMD安装在跨中截面的顶板位置。

3.2 试验加载方案

试验选用激振器提供激振力，激振能量更大，分布更均匀，并有多种激励信号可供选择。在本次试验中选择输出正弦信号，经功率放大器放大，由激振器输出激振力，如图13所示。简谐荷载频率成分单一，但能够明显激起受控模态共振，并且为了研究作用荷载的激振频率对TMD减振效果的影响，减振前后采用相同的激振幅值28 N。

图13 激振力时程曲线Fig.13 Time history curve of force

激振位置选择在跨中截面的钢轨上，如图12所示，以尽可能接近现场的工况，激振位于跨中，能够明显激起2阶受控模态的共振峰值。

4 TMD减振效果分析

4.1 时域分析

测定结构在45～49 Hz的激振频率下，工况一、工况二中测点的振动响应，并绘制安装TMD前后跨中截面翼板在45 Hz，47 Hz和49 Hz的加速度时域响应，如图14所示。可以发现在加速幅值为28 N的正弦荷载激励下，激振频率分别为45 Hz，47 Hz，49 Hz时，减振前翼板测点加速度响应峰值分别为0.144，0.310，0.166，安装1阶模态TMD后，47 Hz减振效果最佳，加速度幅值降至0.084 m/s2。

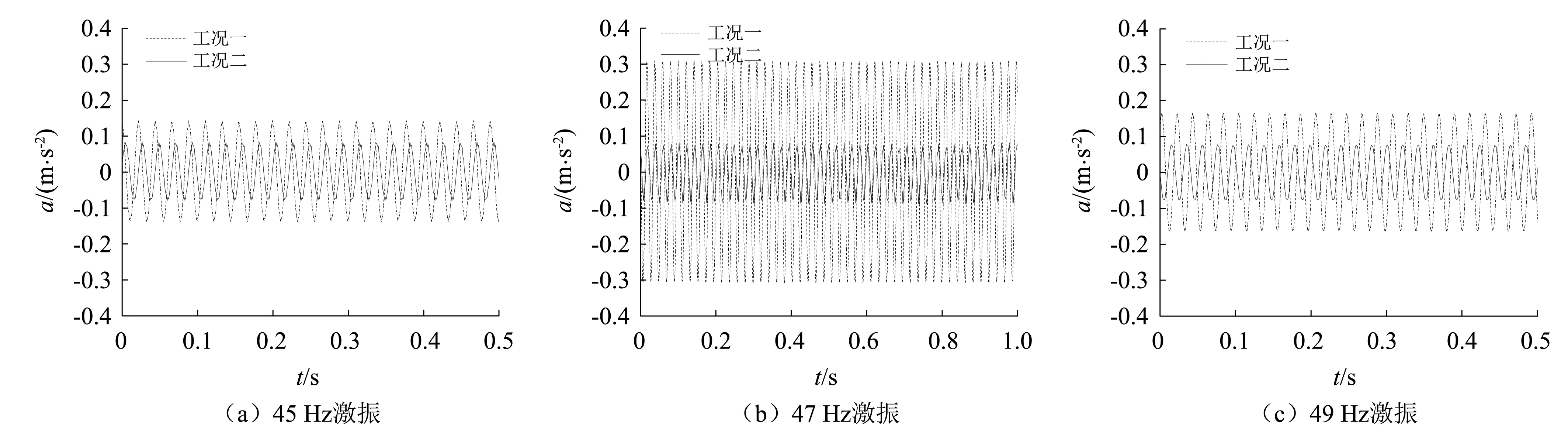
图14 C1加速度时域响应Fig.14 Time-domain response of acceleration at C1

工况一、工况三和工况四中跨中截面翼板测点在54 Hz，55.5 Hz和57 Hz激振下的加速度时域响应，如图15所示。可以发现激振频率分别为54 Hz，55.5 Hz，57 Hz时，安装2阶模态TMD后，加速度时域响应明显降低。并且显然质量比为0.02时TMD减振效果优于质量比为0.01。

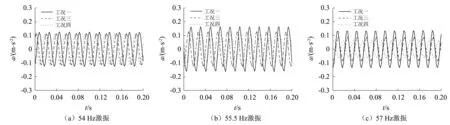
图15 C2加速度时域响应Fig.15 Time-domain response of acceleration at C2

4.2 频域分析

图16和图17分别给出了不同激振频率下工况一与工况二跨中截面翼板测点C1和腹板C2的加速度有效值随激振频率的变化。

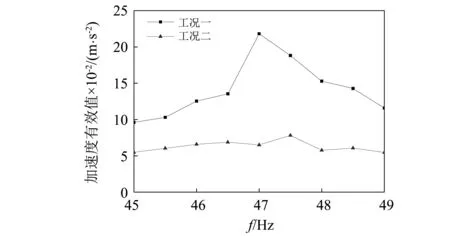
图16 C1测点加速度有效值Fig.16 RMS of acceleration at C1

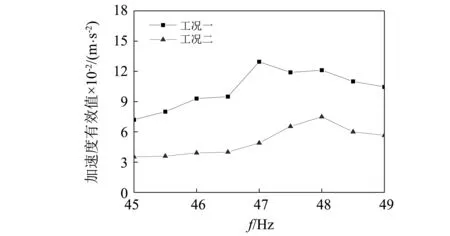
图17 C2测点加速度有效值Fig.17 RMS of acceleration at C2

由图可知，激励点位置的选择能够明显激起1阶模态共振，在分析频段范围内，未安装TMD的轨道箱梁模型翼板和腹板的加速度有效值在47 Hz处出现最大峰值，与1阶固有频率46.654 Hz一致。并且可以发现相对于腹板位置，翼板的峰值体现比较明显，这是因为跨中截面的翼板位置为1阶模态的波腹位置。

轨道箱梁模型安装TMD之后，翼板和腹板的加速度有效值在47 Hz附近得到了明显的抑制，并且安装TMD之后翼板在47.5 Hz出现新的峰值，腹板在48 Hz出现新的峰值，分析原因是附加质量块对桥梁系统的自振特性产生了影响，使共振频率发生了偏移。从图中还可以发现，越接近共振频率，TMD减振效果越好，当激振频率为47 Hz时，未安装TMD时的翼板测点加速度有效值为0.212 m/s2，而安装TMD之后翼板的加速度有效值仅为0.065 m/s2，降幅达到70.2%；腹板测点加速度有效值为0.130 m/s2，而安装TMD之后腹板的加速度有效值仅为0.049 m/s2，降幅达到62.2%。

图18和图19分别给出了不同激振频率下工况三和工况四跨中截面翼板和腹板测点的加速度有效值，并将其与工况一未安装TMD时的加速度有效值进行对比。

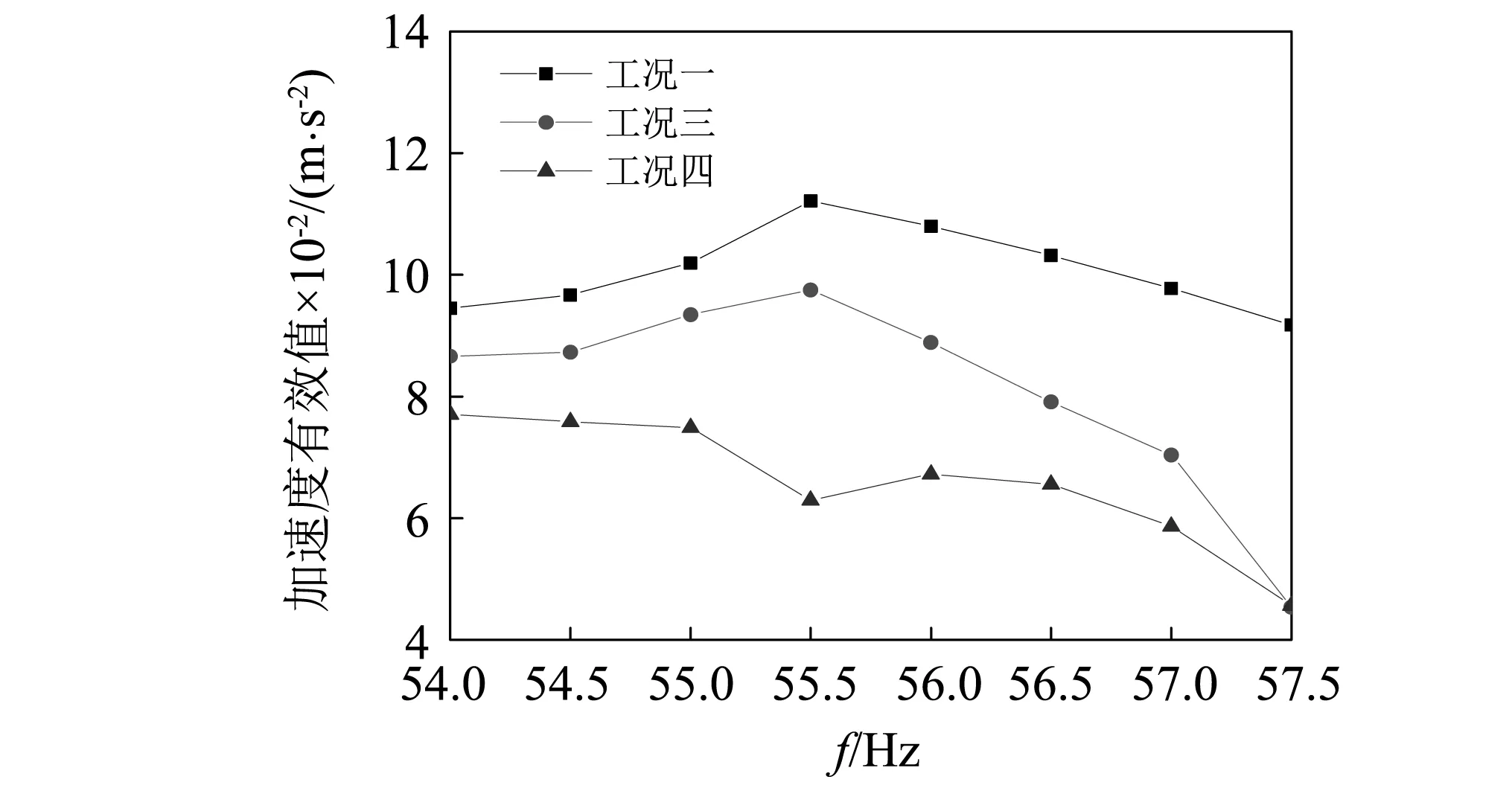
图18 C1测点加速度有效值Fig.18 RMS of acceleration at C1

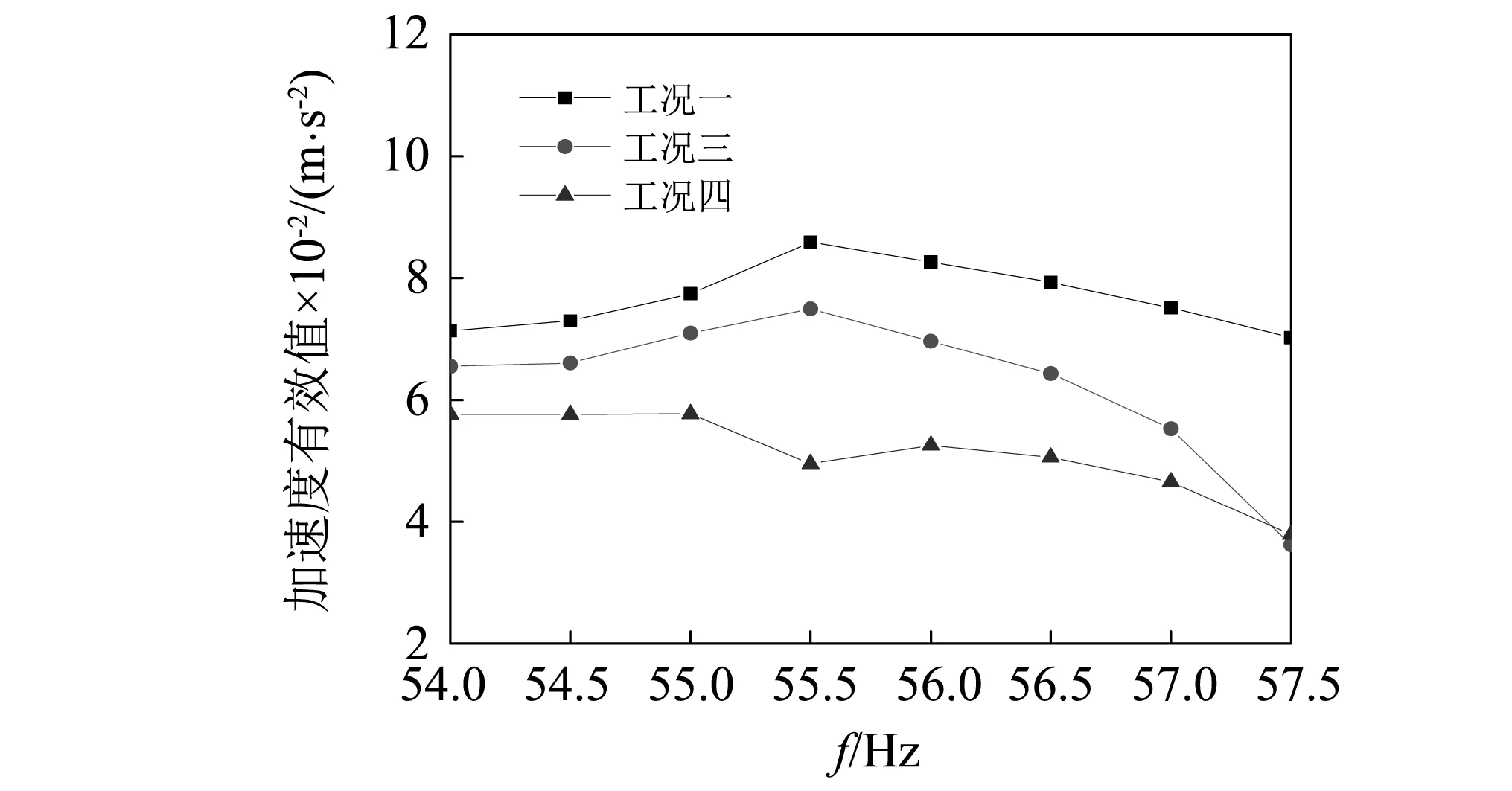
图19 C2测点加速度有效值Fig.19 RMS of acceleration at C2

由图18、图19可知：在分析频段范围内，未安装TMD的轨道箱梁模型翼板和腹板的加速度有效值在55.5 Hz处出现最大峰值，与2阶固有频率55.542 Hz接近。轨道箱梁模型安装TMD之后，翼板和腹板的加速度有效值在55.5 Hz附近得到了明显的抑制，并且质量比为0.02时的减振效果更好。

当质量比为0.01时，减振后测点的振动响应仍然在55.5 Hz激振时出现峰值，减振效果在57.5 Hz激振时效果最佳，减振前翼板加速度有效值为0.091 8，减振后为0.045 3，降幅可达50.7%。腹板加速度有效值为0.070 2，减振后为0.036 2，降幅可达48.4%；当质量比为0.02时，在激振频率为55.5 Hz时减振效果最佳，未安装TMD时的翼板测点加速度有效值为0.112 m/s2，而安装TMD之后翼板的加速度有效值仅为0.062 9 m/s2，降幅达到44.0%；腹板测点加速度有效值为0.085 9 m/s2，而安装TMD之后腹板的加速度有效值仅为0.049 5 m/s2，降幅达到42.4%。