翼板动平衡方法研究
2018-11-14张西宁赵欢夏心锐杨雨薇
张西宁,赵欢,夏心锐,杨雨薇
(西安交通大学机械工程学院,710049,西安)
旋转机械在航空航天、汽车、石油、电力等领域发挥着不可替代的作用[1]。随着现代旋转机械朝高速化、重载化、智能化的方向发展,旋转机械中,转子平稳运行显得尤为重要[2]。由于设计不合理、生产制造以及工作过程中质量颗粒的脱落或吸附都会引起转子部件的失衡,引发系统的强烈振动,加剧转子、密封、轴瓦等的机械磨损,甚至还会诱发其他形式的振动。为了避免发生这些现象,对转子质量分布进行有效改善,研究高效、精确的动平衡方法势在必行[3-4]。
目前,通用的离线动平衡方法主要是加、去重法,难以精确控制去除质量的大小,导致平衡精度较低。在线动平衡装置主要有气体式、液体式、电磁式及机械式[5-9]。气体式动平衡装置结构复杂;液体式平衡过程不稳定;电磁式驱动系统体积大,结构复杂,且平衡能力有限;机械式在高速时配重块难以准确定位,平衡效率较低。
本文提出了一种新的翼板动平衡方法,通过调整周向安装于转子周围的翼板迎角,产生相应的补偿力,对主轴不平衡质量产生的离心力进行平衡。该方法可实现在线动平衡,且平衡头整体结构简单,无需引入其他附加结构。动平衡实验结果验证了本文提出的翼板动平衡方法的有效性。
1 翼板动平衡原理
设想将翼板周向安装于旋转主轴周围,使其弦线与主轴轴线相垂直,而翼展平面与旋转轴轴线平行,此处翼板迎角为翼板弦线与翼板安装点处圆的切线之间的夹角。与圆周切向有一定夹角的翼板在空气中运动时,翼板相对运动方向存在一定的迎角,一方面翼板的迎角变化产生不同大小的离心力,另一方面翼板还会产生垂直于相对来流方向的升力以及平行于相对来流方向的阻力[10]。当翼板的离心力、升力与原始失衡量大小相等、方向相反时,失衡离心力就得到了抵偿。翼板平衡原理如图1所示。

图1 翼板动平衡原理图
1.1 平板形翼板分析
为了方便起见,选用离心力不随迎角变化的平板形翼型,对翼板随主轴旋转时的气动特性进行分析。平板形翼型属于对称翼型,对称翼型具有如下的气动特性[11]:升力系数与几何迎角成正比;几何迎角为0时,升力系数亦为0,即0升力迎角为0°;翼型的压力中心和气动中心处于同一点[12]。
本文随主轴旋转做圆周运动的平板形翼板升力计算公式如下
FL=ρν2sL/2=ρω2R2sL/2
(1)
式中:FL为升力;L为升力系数;ω为转轴转速;ρ=1.29 kg/m3为空气密度;R为翼板几何中心到转轴距离;s为翼板面积。其中,对称形翼板的升力系数为
L=2πα
(2)
式中:α为翼板迎角。
平板形翼板的阻力系数为[13]
D=2sin2α
(3)
由于4个翼板两两180°相对安装,相对翼板产生的阻力方向相反,形成阻力矩,对所能提供的平衡量不产生影响。不平衡质量所产生的离心力为
F=mω2r
(4)
式中:m为不平衡质量;r为不平衡质量到转轴的距离。
单个翼板提供的平衡量与翼板迎角、转子转速、翼板安装半径的关系如下
(5)
式中:m′为翼板提供的等效平衡质量,m=m′。
由式(5)可知,平板形翼板产生的升力所等效的补偿质量与翼板面积、迎角及安装半径的平方成正比。增大翼板面积和安装半径可以提高翼板所产生的升力及其等效的补偿质量。
在翼板随主轴转动过程中,不仅存在升力和阻力,还存在离心力。翼板相对迎角为α时的离心力如图2所示,其竖直分量为
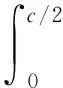


(6)
式中:h为翼板厚;c为翼板弦长。翼板离心力水平分量为
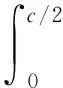
(7)

图2 平板形翼板离心力分析示意图
由式(6)可知,无论翼板迎角为多少度,其所受的离心力在竖直方向分量不变即为常量。由式(7)可知,翼板不同迎角的离心力水平分量皆为0。综上所述,平板形翼板的离心力不随翼板迎角的变化而变化。在平板形翼板动平衡过程中,翼板提供的补偿质量都是翼板所受升力的等效补偿质量,因而采用平板形翼板可研究升力提供的补偿质量及平衡机制,并从侧面验证了平板的气动特性。
1.2 圆弧形翼板分析
为提高翼板的平衡能力,对翼板翼型进行改进。翼板在动平衡过程中,实际线速度较低,因而雷诺数相对较小,而圆弧翼型[14](弯板翼型)具有良好的低雷诺气动性能,且圆弧形翼板易于加工,不需要借助模具,更具有优势[15],因而选择圆弧形翼板作为动平衡基本翼型装置。圆弧形翼板在提供相对更大的升力同时,产生的离心力也可提供一定的平衡力,共同实现平衡补偿。
圆弧形翼板在随主轴旋转时,翼板产生升力外还产生离心力。升力所提供的等效平衡补偿质量如下
(8)
式中:s=2.29×10-2m2为面积;R=0.09 m;r=0.04 m。经计算得到m′=2.29L。
圆弧形翼板以一定的迎角随主轴旋转时产生的离心力,如图3所示。
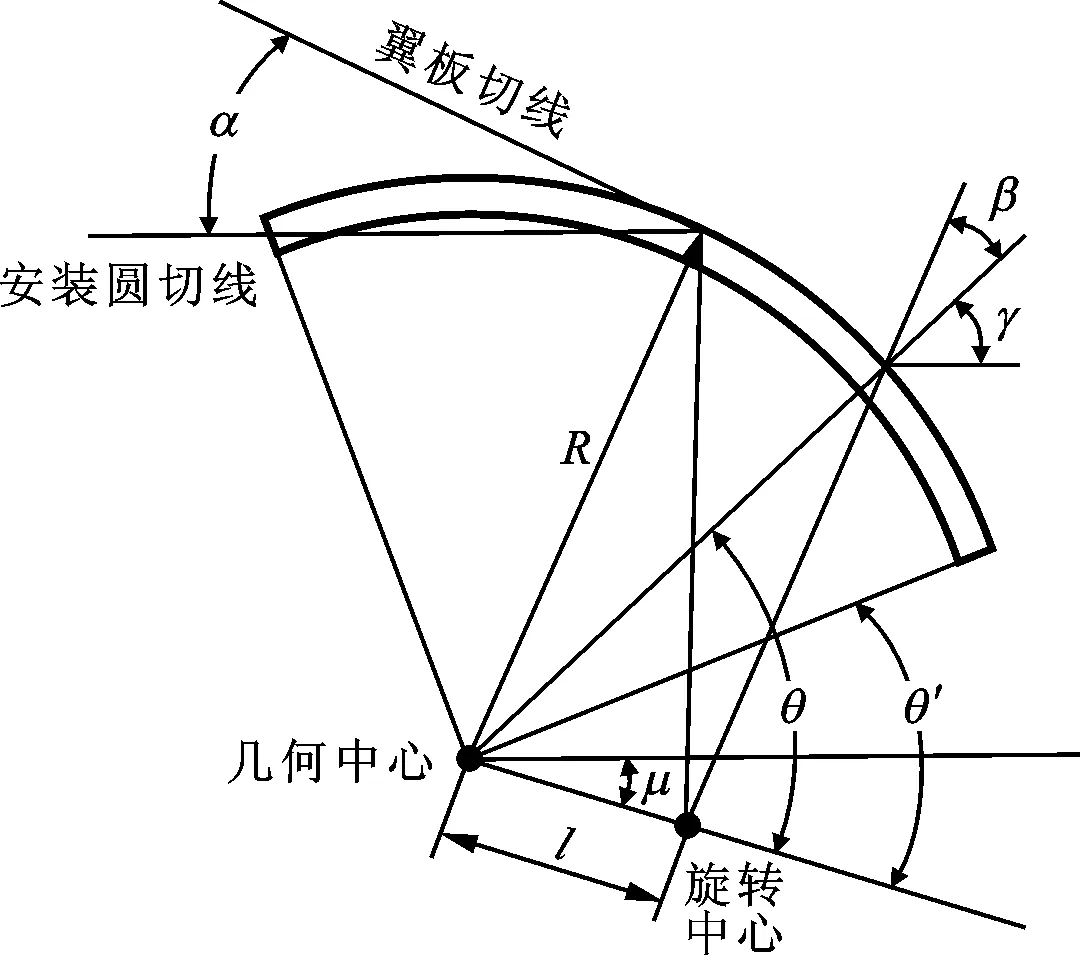
图3 圆弧形翼板迎角为α时的离心力计算示意图
当翼板迎角为α时,离心力为

(9)
式中:l为翼板旋转中心到几何中心的距离;θ为几何中心与旋转中心的连线与翼板相对旋转中心最低点处的旋转半径夹角。
图3中,μ为几何中心与旋转中心的连线与水平线夹角,根据圆弧形翼板的安装与旋转中心的几何关系,有μ=α/2,θ′=π/4-μ,可得
(10)
相应的,翼板离心力的水平分量为
(11)
由式(10)可知,圆弧形翼板的离心力难以用解析解表达,且翼板产生的离心力方向分布不一致。利用Matlab求出式(10)和式(11)的数值解。
翼板平衡装置由4个翼板两两相对布置,当单个翼板迎角变化提供补偿质量时,其余3个翼板保持0°迎角不变。此处翼板迎角为翼板在安装点处翼板切线与安装圆切线的夹角。以该点处安装圆切线为参考,翼板前端(相对来流方向)偏离该圆时,迎角为正,偏向该圆时,迎角为负,如图3所示,翼板迎角为正。
单个翼板工作时,翼板的安装位置为0°,翼板的离心力和与其180°相对的翼板离心力合成,得到单个翼板工作时离心力所能提供的补偿质量和角度如表1所示。
由于翼板180°相对安装,表1中单个圆弧形翼板作用是指在其他3个翼板迎角都为0时,只调整一个翼板的迎角,该翼板平衡装置所能提供的补偿质量。在该翼板迎角为0°时,平衡头产生的补偿质量亦为0。根据表1,拟合出单个翼板离心力等效的补偿质量与翼板迎角的关系为m=|1.17α|+0.5,α≠0,拟合出单个翼板离心力等效的平衡角度与翼板迎角关系为
当α=0时(初始状态),有m=0,δ=0。

表1 单个圆弧形翼板离心力提供的补偿质量
2 翼板流场仿真分析
2.1 平板形翼板仿真分析
对所设计的翼板进行流体仿真计算,以验证其气动特性[16-20]。平板形翼型形状简单,因而直接在gambit软件中进行翼板的几何建模,用四边形结构网格绘制O型远场网格。O型远场网格区域的直径是所设计翼板弦长的10倍,网格形状如图4所示。

图4 平板形翼板网格划分图
将划分好的网格导入fluent软件,进行下一步数值模拟计算[19]。计算中,湍流模型选择无黏模型inviscid,即忽略空气的黏性作用,设置远场边界为压力远场,操作压强为默认值101 325 Pa,显示压强设置为0 Pa。翼板设定为静壁面类型,对主轴转速为3 000 r/min状态下的翼板进行数值模拟计算。fluent计算迎角为5°时的升力系数如图5所示。
根据升力曲线可知,当翼板迎角为5°时,计算所得升力系数为0.27。翼板弦长为100 mm,展长为124 mm,面积为0.012 4 m2,翼板安装中心距离转子轴心为0.09 m,计算主轴转速为3 000 r/min时,平板形翼板的升力为

翼板迎角为5°时的压力分析图如图6所示。
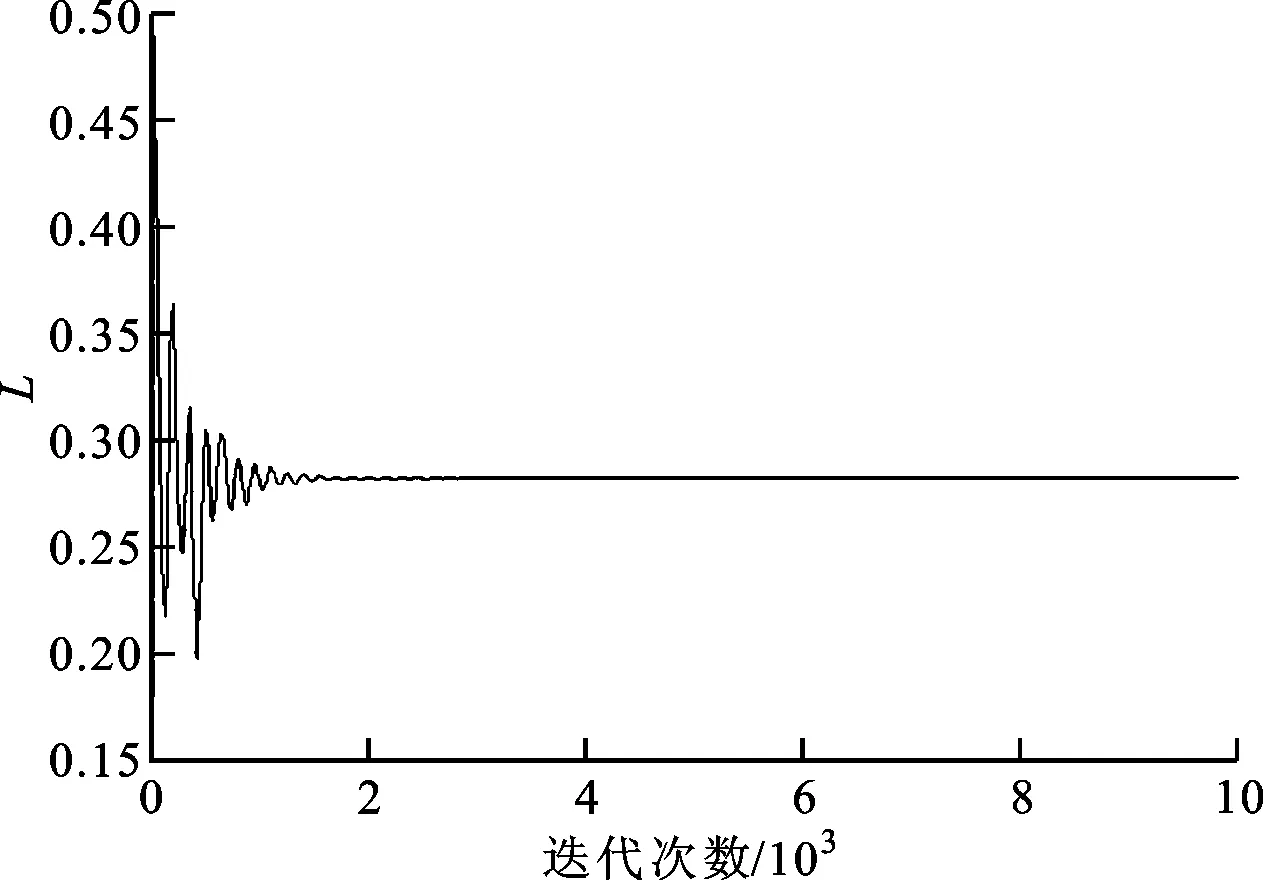
图5 平板形翼板迎角5°时的升力计算结果

图6 平板形翼板压力分析结果
翼板下表面压力pd大,上表面压力pu小,上、下表面压强差大约为260 Pa,但是压力差主要作用于翼板前缘,即受力面积为翼板面积一半。应用压力和压强转换公式,将压强差折合为压力差,得到FL=(pd-pu)s=260×0.012 4÷2=1.612 N。该值与用升力系数计算所得升力大小相符,说明仿真计算过程正确。

图7 圆弧形翼板压力分析结果
2.2 圆弧形翼板仿真分析
圆弧形翼板迎角为0°时的压力分析图如图7所示。根据压力分布图,计算翼板的升力为
FL=(pd-pu)s=91.73 N
(12)
根据所得升力,估算圆弧形翼板的升力系数如下
(13)
圆弧形翼板的升力系数在翼板迎角为0°时为1.57。4个翼板两两对称布置,当翼板迎角为0°时,各翼板所产生的升力相互抵消,对平衡过程不产生影响,因而作为初始状态。
3 翼板平衡力测试
3.1 平板形翼板测试
平板形翼板动平衡部件在立式动平衡机上进行组装,如图8所示。连接轴安装于平衡机主轴上,由3个螺钉紧定连接轴,以保证其相对平衡机不发生滑移。翼板支架、连接轴、轴套之间的接触面间安装有橡胶垫片,增加了平衡头与平衡机主轴的摩擦力,使平衡头与主轴同步旋转。平衡机与翼板平衡头的连接轴上设有螺纹孔,以进行系统初始不平衡量的检测,并对翼板平衡装置引入的附加不平衡量进行平衡。平衡头的翼板从0°以逆时针方向编号,依次为1、2、3、4。

图8 平板形翼板平衡头装配图
在800 r/min下对翼板进行实验测试。以5°为间隔调整一个翼板(翼板2),分析其产生的补偿质量。翼板2的不平衡质量为调整翼板2后所得补偿质量与初始状态(翼板迎角为0°)不平衡质量相减所得到的补偿质量及相位,各迎角下的分析结果如图9所示。图9a中不同翼板迎角提供的补偿质量与初始状态相连接,以直观判断所产生的补偿质量相位关系。
由翼板2的不平衡量可知,迎角相反时所提供的补偿质量相位相反,且理论计算、仿真分析以及平衡机测试结果趋于一致。
对与翼板2相对的翼板4进行平衡能力测试,得到实验结果如图10所示。与图9a同理,图10a中迎角正负不同时,所产生的平衡力也相反。

(a)不平衡量
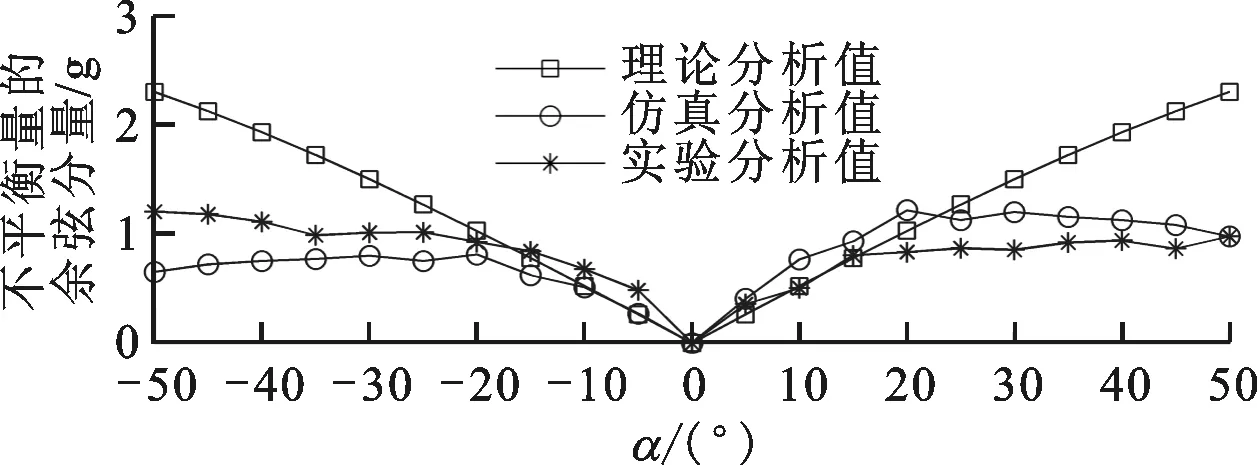
(b)补偿质量图9 调整翼板2补偿质量的变化情况

(a)不平衡量
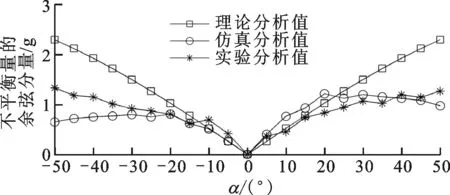
(b)补偿质量图10 调整翼板4补偿质量的变化情况
对比图9a、图10a可知,两个相对的翼板迎角相同时,所产生的平衡力方向相反。
3.2 圆弧形翼板测试
圆弧形翼板平衡装置安装于改装的钻床,如图11所示,同3.1中平板形翼板平衡能力测试方法相同,进行圆弧形翼板的平衡能力测试。

图11 圆弧形翼板实验台
分别单独调整处于0°(键相位置)的翼板1和处于180°的翼板3的迎角,共同调整翼板1和3相同的迎角或相反的迎角,补偿质量与迎角关系如图12所示。

图12 圆弧形翼板补偿质量与翼板迎角的关系
由图12可知,单个圆弧形翼板的平衡质量可达38 g,翼板1提供的补偿质量与迎角关系为m=0.53|α|+0.41,α≠0。初始时,α=0,m=0。
翼板3的补偿质量与迎角的关系为m=0.54|α|+0.98,当两相对翼板迎角互为相反数共同作用时,补偿质量和迎角的关系为m=1.09|α|+1.14。
两个180°相对的翼板离心力在迎角相同时大小相等、方向相反,相互抵消,不提供平衡质量,在迎角互为相反数时提供的补偿质量倍增。
4 翼板动平衡实验
在钻床上进行圆弧形翼板动平衡实验测试,分别在8个不同的角度添加不同的试重,以模拟主轴产生的不平衡质量。根据图12中补偿质量与翼板迎角相对应的数学关系,对相应的翼板进行调整,具体调整方法及平衡效果如表2所示。
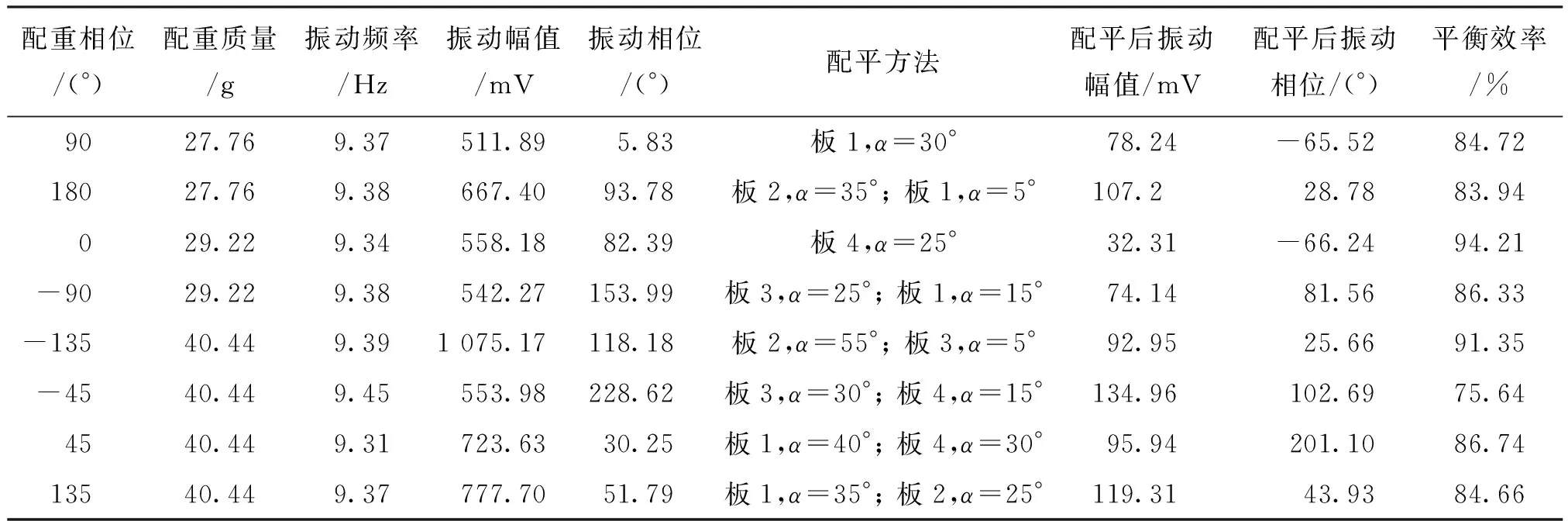
表2 翼板具体调整方法及平衡效果
由表2可知,翼板平衡装置可对主轴上任意相位的不平衡质量进行有效平衡,平衡的不平衡质量达40.44 g,平衡能力为1 617.6 g·mm。
5 结 论
本文提出了一种新的翼板动平衡方法,并设计了翼板动平衡装置。通过调整安装于旋转主轴周围的翼板迎角,进行补偿质量的调整,分析翼板迎角与补偿质量之间的关系,建立翼板迎角与不平衡质量之间的数学模型,从实验上验证了采用翼板进行主轴动平衡的可行性。
设计了4个互成90°安装的翼板平衡头装置,实现对任意大小和方向失衡量的补偿校正。与现有的平衡装置相比,该装置结构简单,安装方便。
从fluent软件数值计算得到的翼板工作过程中的流场状况符合理论计算,验证了翼板平衡方法的可行性。
动平衡实验结果表明,在钻床转速为560 r/min时,校正后振动幅值下降达94.21%,平衡能力高达1 617.6 g·mm,验证了本文提出的动平衡方法。
