不同正则化方法在船舶辐射噪声计算中对比与试验研究

2021-09-27李瑞彪卜文俊徐荣武

振动与冲击 2021年16期

李瑞彪，何琳，卜文俊，徐荣武

(海军工程大学船舶振动噪声重点实验室，武汉 430033)

船舶在满足航行及船员舒适性要求前提下，其水下辐射噪声也显得尤为重要，尤其是对于科考船、军用舰艇等，水下辐射噪声也是船舶的核心指标[1]，决定着船舶的综合声学性能，直接影响船舶作业和作战能力。因此，实时预报船舶自身辐射噪声水平，尤其是重要特征频段或线谱，对于指导船舶降低辐射噪声，提高船舶综合声学性能具有重要意义[2]．

曹跃云等[3-4]基于工况传递路径分析 (operational transfer path analysis,OTPA)法开展噪声源贡献、载荷识别、传递路径分析等应用研究。而在船舶辐射噪声评估中，OTPA法基于“响应-传递路径-响应”模型[5]，以测得的船舶自噪声或振动加速度响应为输入，远场辐射噪声响应为输出，通过预先求解输入响应与输出响应之间的辐射噪声传递函数来实时预报辐射噪声。

OTPA模型的关键是求解传递函数，本质属于反问题，不同领域的研究者针对不同的应用场景提出了奇异值分解(singular value decomposition,SVD)方法、Tikhonov正则化等求解方法，以提高传递函数求解精度。Golub等[6]针对病态问题求解提出了GCV正则化参数求解方法；Hansen等[7-8]针对病态问题研究了L-curve、广义交叉验证(generalized cross validation,GCV)等正则化参数求解方法，并讨论了L-curve和GCV两种正则化参数求解方法在不同背景干扰下的性能；郭荣等[9]研究了基于SVD和Tikhonov正则化的载荷识别方法，并基于平板载荷识别仿真和简支梁载荷识别试验讨论了噪声对SVD、L-curve方法的影响；Cheng等[10]针对传统OTPA采用SVD法求解传递函数的不足，提出了Tikhonov正则化方法，并基于球形声源仿真和圆柱壳结构振动传递试验对比研究了GCV正则化参数求解方法。

而受制于船舶辐射噪声测试及应用条件，船舶噪声源及其复杂，工况数据输入往往包含较强的海洋环境背景噪声[11-12]。针对船舶水下辐射噪声评估应用，目前，讨论基于不同正则化方法在不同噪声背景下求解水下辐射噪声传递函数的公开报道较为少见。基于此，本文结合船舶实际工程应用，考虑不同背景噪声环境对辐射噪声传递函数的影响，在理论上系统分析SVD和Tikhonov正则化方法，提出简化的准最优判别准则正则化参数求解方法；同时，设计双层圆柱壳缩比舱段模型，用于模拟船舶运行工况，并在千岛湖开展水下声辐射测试试验，验证不同方法在不同噪声下的适用性。

1 基于OTPA的船舶辐射噪声评估方法

1.1 OTPA理论

通过改变船舶航速、设备开启状态等设计若干噪声测试工况，建立壳体振动加速度响应与目标点辐射噪声响应间的传递关系。则OTPA模型可表示为

(1)

式中：Tj(ω)为第j个壳体响应到目标点辐射噪声响应的系统传递特性函数；Xkj(ω)为第k个工况下第j个传感器测得的壳体振动加速度响应；Yk(ω)为第k个工况下距离船舶正横方向1 m处的目标点水听器测得的辐射噪声响应；j=1,2,…,m，k=1,2,…,r。式(1)简化成矩阵形式为

Xr×mTm×1=Yr×1

(2)

对式(2)求解，则系统传递函数矩阵Tm×1(ω)为

(3)

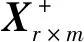
假设求得辐射噪声传递函数之后，在航行中获得某工况下船舶振动响应为Xtest(ω)，则目标点辐射噪声响应Ytest(ω)可表示为

Ytest=XtestTm×1

(4)

1.2 SVD方法

OTPA模型的关键是辐射噪声传递函数的求取，传统OTPA通常采用SVD方法计算辐射噪声传递函数Tm×1，对Xr×m进行奇异值分解，即[13]

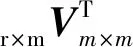
(5)

式中：Ur×r和Vm×m为酉矩阵；∑r×m可表示为

∑r×m=diag(σ1,σ2,…,σj,…,σm)

(6)

式中：σj为第j个奇异值，且满足σf≥σj+1≥0。定义累计贡献率(cumulative contribution rate，CCR)作为确认主奇异值数量的指标，目前工程上一般设RCC(L)≥85%[14]，则RCC(L)可表示为

(7)

对应选取前L个奇异值，则传递函数Tm×1为

(8)

式中，Vm×L与Ur×L分别为选取矩阵Ur×r和Vm×m的前L列向量构成的矩阵，化简为

(9)

式中，Uj和Vj分别为酉矩阵Ur×r和Vm×m的第j列向量。但是在船舶辐射噪声测试中，无论是测得的辐射噪声响应还是振动加速度响应，都掺杂有海洋环境背景噪声，会导致系统出现不同程度的病态性，其可以用条件数cond(X)表示，即[15]

(10)

通常认为，当cond(X)<100时，系统为良性，当cond(X)处于100～1 000时，系统为中等程度病态；当cond(X)>1 000时，系统为严重病态。式(10)中，当σm趋于0，则系统为严重病态，此时，SVD由于没有充分考虑环境噪声扰动等因素带来的误差影响，式(2)的解也会失去物理意义，辐射噪声评估误差也会较大。

2 Tikhonov正则化方法

2.1 Tikhonov正则化理论

在实际工程应用中，假设评估得到的辐射噪声传递函数为Tλ，定义误差函数e为

e=XTλ-Y

(11)

为使得误差函数e最小，Tikhonov正则化方法引入参数λ用于平衡解的拟合程度和稳定性，则Tikhonov正则化公式可定义为

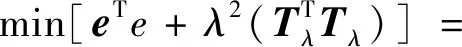
(12)

式中，‖XTλ-Y‖2与‖Tλ‖2分别为残差范数和解范数。对函数J(λ)求一阶导数，且仅当一阶导数为0时，J(λ)最小，此时对应的Tλ为最优正则化解，即

(13)

对式(13)进行化简，即

(XTX+λ2Im)Tλ-XTY=0

(14)

式中：Im为m阶单位矩阵；辐射噪声传递函数Tλ为

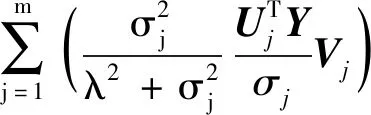
(15)

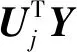
(16)

(17)

在式(16)与式(17)中，M=UTY=[M1,M2,…,Mm]T。Tikhonov正则化与SVD方法相比，其通过参数λ平衡解的拟合程度和稳定性，充分考虑了辐射噪声传递函数求解过程中由于解的不稳定性和环境噪声等因素带来的误差影响。Tikhonov正则化方法的关键是选择参数λ，因此，借鉴病态逆问题求解的GCV和L-curve正则化参数λ求解方法，计算最优正则化参数λ以降低辐射噪声计算误差。

2.2 GCV方法

从式(13)可看出，正则化参数越大，正则化程度越大，噪声越小，但是正则化误差越大，反之则相反。GCV方法通过广义交叉验证寻找最合适的正则化参数λ，其表达式可表示为

(18)

式中，trace(·)为矩阵的迹，表示矩阵对角线元素之和；Ir为r阶单位矩阵；Xλ满足Tλ=XλY，即

Xλ=(XTX+λ2Im)-1XT

(19)

则矩阵的迹可转化为

trace(Ir-XXλ)=trace[Ir-X(XTX+λ2Im)-1XT]=

(20)

当GCV(λ)取最小值时所对应的参数λ即为GCV确定的最优正则化参数，其不需要对原始数据中误差进行先验估计或假设，但当数据变化非常平缓时则不易求解。

2.3 L-curve方法

在求解正则化参数λ过程中，参数λ决定着残差范数和解范数的大小，最直观的操作是获得一个最优参数λ使得两者都同时达到最小，而L-curve方法则正是以图示方式直观的显示了以参数λ为变量的解范数和残差范数之间的关系，定义残差范数函数和解范数函数

(21)

式中，ρ(λ)和η(λ)均为参数λ的函数。L-curve方法以lg[ρ(λ)]为横坐标，lg[η(λ)]为纵坐标作曲线，曲线形状类似“L”，当λ使得lg(ρ(λ)]和lg[η(λ)]同时最小时便为最佳正则化参数，该点恰为L曲线曲率最大点，则L曲线曲率计算公式可表示为

(22)

L-curve方法与GCV方法相比，其同时考虑了残差范数与解范数，可最大程度上调整数据拟合度部分与解间的平衡，适用于高噪声背景下求解。

3 舱段模型试验

3.1 试验概述

为对比不同方法在不同噪声背景下的辐射噪声评估性能，设计了缩比舱段模型，并在千岛湖水声试验场开展了水下声辐射测试试验，舱段模型示意图，如图 1所示。

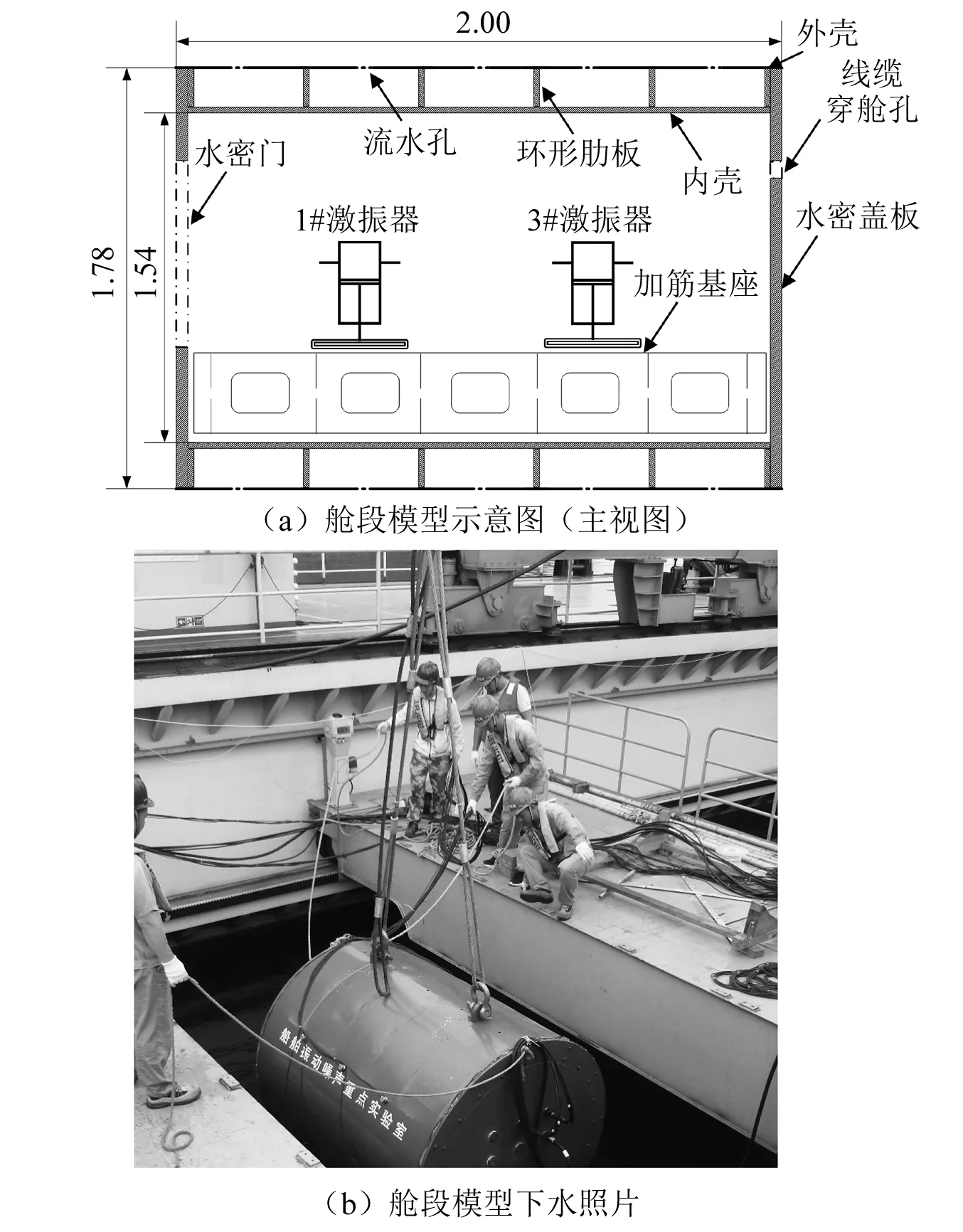
图1 舱段模型示意图及下水照片(m)Fig.1 The schematic diagram and launching of cabin model(m)

从图1(a)可知：舱段模型为双层圆柱壳结构，舱段外径1.78 m，内径1.54 m，长2.00 m，外壳与内壳通过6个环形肋板焊接相连，肋板沿轴向等间距分布。艏端水密门用于试验期间调试、更换试验设备，与壳体法兰通过螺栓连接，艉端水密盖板与舱段通过螺栓连接，并设计6个线缆穿舱孔，用于舱内激振器、传感器及泄漏监测报警器等设备线缆与外部岸上试验平台连接。试验期间，舱段内外壳之间为充水状态，其通过外壳体上下表面的10个流水孔注排水，如图1(b)所示，舱段模型通过钢缆下放，水下吊放深度为25 m(舱段中心轴距水平面距离)，更换试验设备时，可将舱段提升至试验平台上，打开水密门进行更换和调试。

3.2 工况设计

舱段模型内部安装4台激振器，用于模拟船舶机械设备工作，如图 2所示。1#激振器、3#激振器布置在左舷，2#激振器、4#激振器布置在右舷，激振器激振频率范围100～2 000 Hz，最大激振力500 N。

试验期间，1#激振器与2#激振器可通过预制的垫板增加单层橡胶隔振器或双层隔振装置来调整安装状态，实现激振器刚性和弹性安装的切换，以模拟船舶上设备隔振或安装状态变化情况。舱段模型外壳表面布置15个湿端加速度传感器，如图 2所示，编号为32#～36#，沿轴向均匀布置3圈，每圈5个传感器，用于测量舱段模型外壳体振动。以图2(a)中标注的“34(35)”为例，其表示34#传感器与35#传感器沿中轴面对称布置，其中34#传感器位于模型上侧，35#传感器位于模型下侧。在两侧正横方向上布置两个水听器，编号为48#～49#，距舱段外壳分别为6 m和10 m，用于测量舱段模型向水中辐射的噪声。

试验中分别以采集的经过预处理后的不同转速下机械设备振动信号、扫频信号(频率间隔为1 Hz)为激振器输入激励源，通过位于试验平台上的B &K PULSE发射激励信号，改变激振器安装状态，同时，作为对比，选择若干施加不同高斯白噪声作为环境扰动，改变不同工况信噪比，用于对比不同方法在不同噪声下的适用性，共计100余组组合工况。其中，激振器安装状态的调整可通过在试验平台上打开水密门更换1#隔振器与2#隔振器的隔振装置进行。另外，试验中正常环境下背景噪声约为103.75 dB (100～2000 Hz)，信噪比≥20 dB。信号采样频率为8 192 Hz，每组工况信号采集时间100 s。

4 不同背景噪声下辐射噪声评估结果对比

随机选择若干组工况，分别采用不同方法评估辐射噪声，并添加不同噪声等级的噪声扰动，对比分析正常环境和添加噪声扰动下不同方法的辐射噪声评估误差。定义累计误差用于衡量辐射噪声在全频段误差的大小，公式为

(23)

式中：Ytest,i为第i个频率点辐射噪声声压谱级评估值；YM,i为第i个频率点辐射噪声声压谱级实测值；N为频率点数。需要说明的是，试验中辐射噪声声压级均为48#、49#水听器所测声压级按照球面波衰减规律归一化为距离舱段模型1 m处距离处声压级的平均值。

4.1 正常环境下辐射噪声计算结果对比

随机选择两个工况分别命名为1#工况和2#工况，采用不同的方法评估辐射噪声，声压谱级图对比，如图 3所示。从1#、2#工况对比结果可知：与L-curve和GCV方法相比，SVD方法部分频点计算结果与实测值在全频带上吻合较差，最大误差分别为16.73 dB，26.55 dB，较L-curve方法计算误差分别大7.70 dB，17.60 dB，较GCV方法计算误差分别大2.11 dB，16.67 dB。

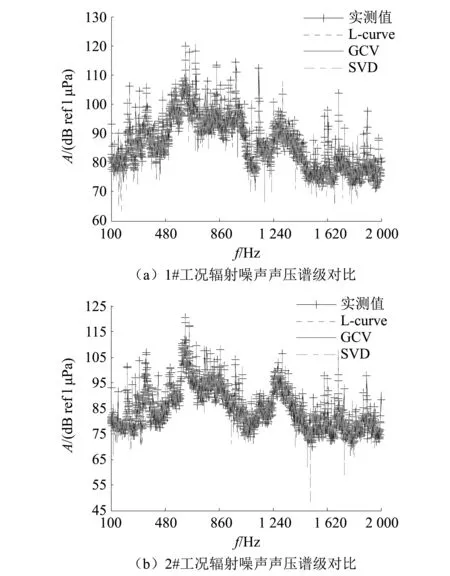
图3 辐射噪声声压谱级对比Fig.3 Comparison of radiated noise pressure spectrum levels

进一步分析不同方法辐射噪声计算的累计误差，如表1所示。正常环境条件下，基于GCV方法与L-curve方法得到的辐射噪声计算误差基本相同，而SVD方法与GCV方法和L-curve方法相比，1#工况辐射计算误差大约为0.83 dB，2#工况辐射噪声计算误差大约为0.90 dB。

表1 正常环境下辐射噪声累计误差对比Tab.1 Comparison of cumulative errors under normal conditions

经过对比分析，在正常环境下，SVD方法较L-curve与GCV方法评估性能差，而L-curve与GCV方法两者的累计误差基本相同，辐射噪声计算最大误差较GCV方法小约0.93～5.59 dB，其主要是由于系统在不同频率点受湖试中其他噪声干扰，不同频率点的病态程度不同。以1#工况条件数分析为例，在部分频率点上，系统条件数大于1 000，处于严重病态，约占全频带的4.6%，此时极小的环境环扰动也能增大辐射噪声计算误差，如图4所示。同时，分析条件数和计算误差都较大的频率点处的皮卡德条件，如图5所示，离散傅里叶系数趋于0的速度没有奇异值趋于0的速度快，此时基于Tikhonov正则化方法计算得到的近似解受环境扰动严重，但由于L-curve方法较GCV方法和SVD方法，同时考虑了残差范数与解范数，可近似得到最优的正则化参数，最大程度上降低辐射噪声计算误差受解的不稳定性和环境噪声等因素带来的影响。

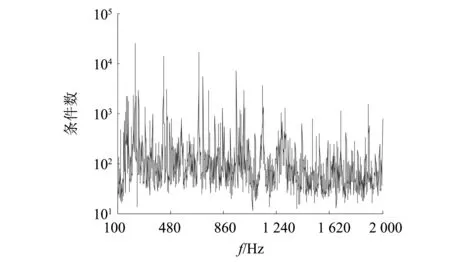
图4 1#工况条件数分析Fig.4 Condition number analysis of operating condition 1#

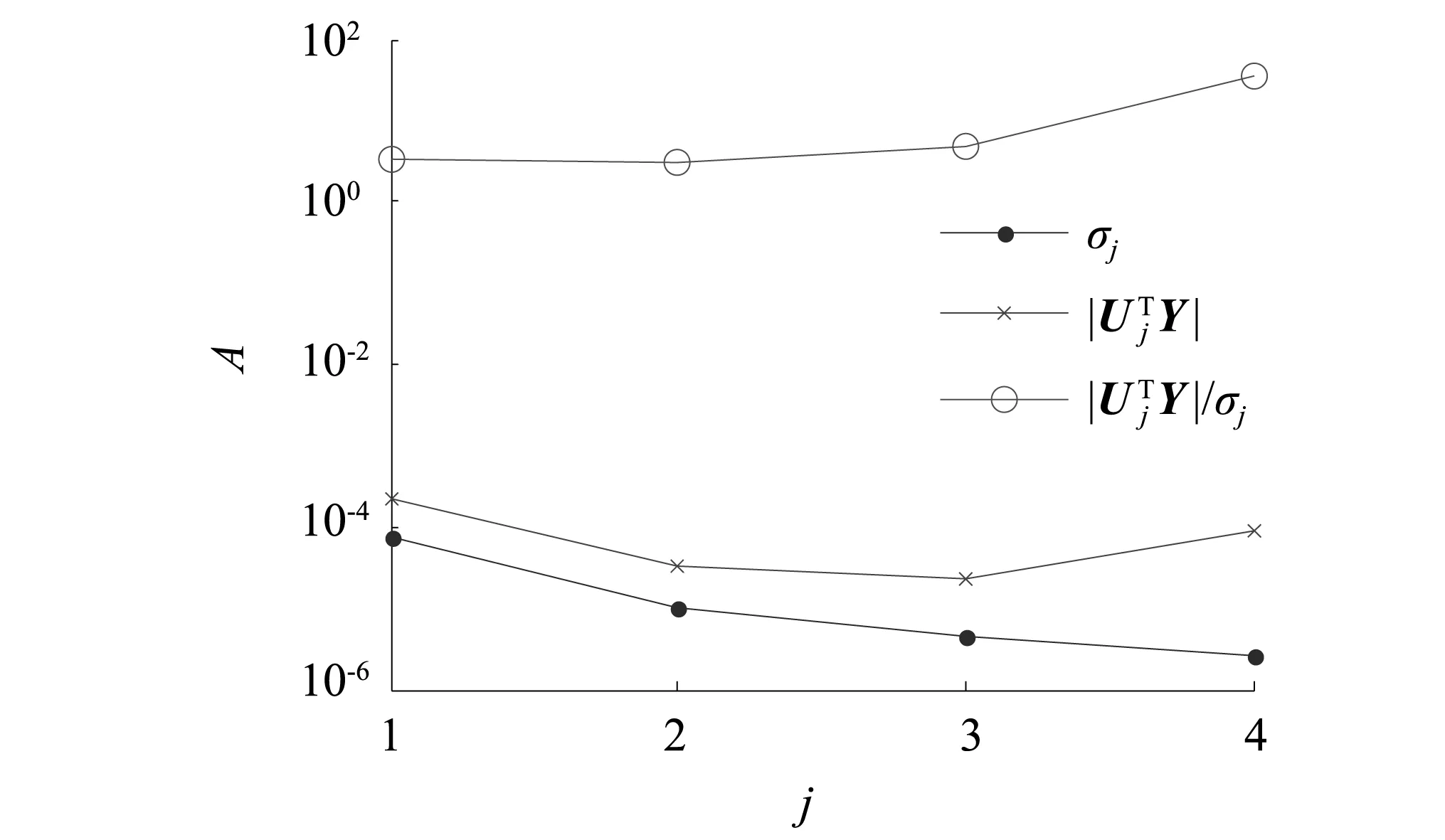
图5 离散皮卡德条件分析Fig.5 Analysis of discrete Picard condition

4.2 不同背景噪声下辐射噪声计算结果对比

为进一步对比不同方法计算得到的正则化参数在不同背景噪声环境下的适用性，试验中分别向振动加速度响应施加5 dB，10 dB，20 dB的高斯白噪声，辐射噪声响应施加5 dB，10 dB，15 dB的高斯白噪声作为环境扰动。分别计算基于不同方法的辐射累计误差，如表2所示。随着输出响应中噪声水平的增大，辐射噪声计算误差也不断增大，而输入响应中噪声变化对辐射噪声计算误差几乎无影响，主要是由于当系统条件数过大时，远场辐射噪声响应有微小的误差或扰动时，经过计算，传递函数T的误差将会被严重放大。从表 2可知：对于1#工况，L-curve方法在低噪声背景下辐射噪声累计误差较GCV方法小约0.13 dB，较SVD方法小约1.02 dB，在高噪声背景下较GCV方法小约0.28 dB，较SVD方法小约0.77 dB。对于2#工况，L-curve方法在低噪声背景下辐射噪声累计误差较GCV方法小约0.11 dB，较SVD方法小约0.74 dB，在高噪声背景下较GCV方法小约0.29 dB，较SVD方法小约0.85 dB。

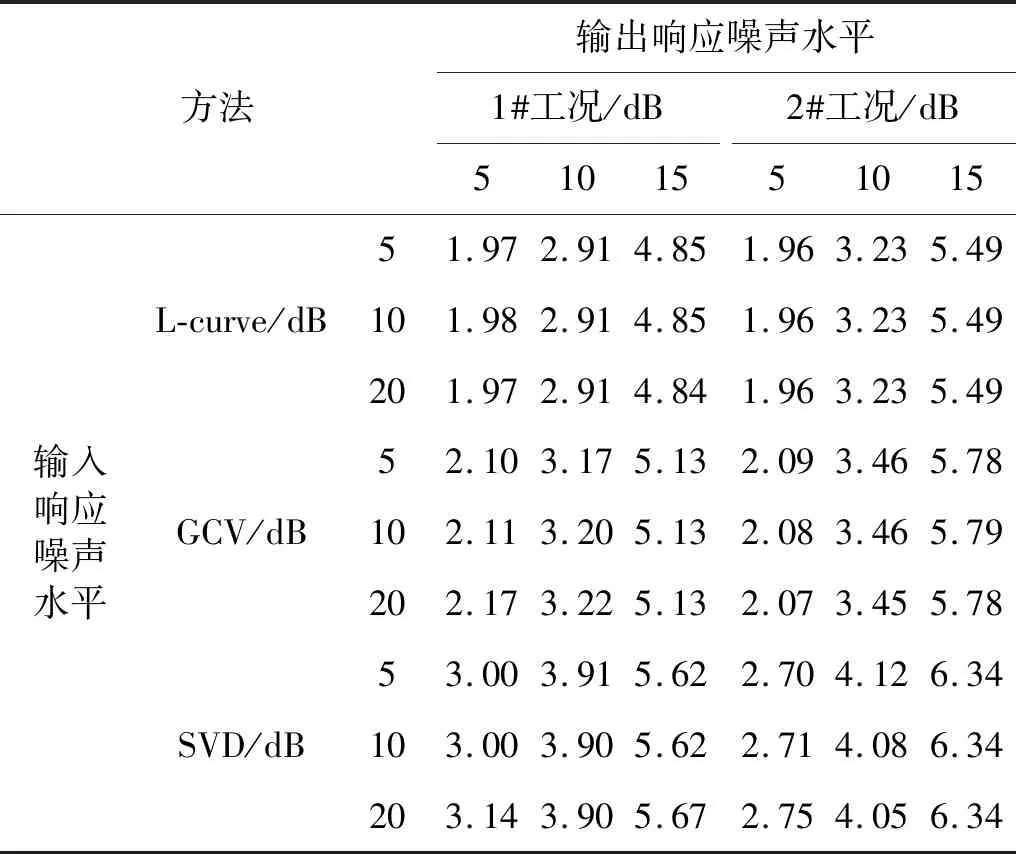
表2 不同背景噪声下辐射噪声累计误差对比Tab.2 Comparison of cumulative errors under various noise levels

可见，与正常环境的辐射噪声计算误差相比，随着环境扰动的增大，其对辐射噪声计算误差的影响也在不断增大，主要原因是在病态系统条件下，基于SVD和Tikhonov方法计算得到的是近似解，而扰动增大，会加剧解的不稳定性，而综合对比，在相同背景噪声环境下，L-curve方法可最大程度上调整数据拟合度部分与解间的平衡，抗环境扰动性能最好，而SVD方法最差。

5 准最优判别准则

第4章对比了不同正则化方法在不同背景下的辐射噪声评估误差，Tikhonov正则化的本质是在不断优化正则化参数，而随着正则化参数的变化，误差也随着增大或减小。因此，本节在系统分析误差来源基础上，进一步提出准最优判别 (quasi-optimality,Q-O)准则以寻找接近最佳的正则化参数，并通过水下辐射噪声试验分析计算误差。

5.1 Q-O判别准则理论

分析基于正则化方法求解辐射噪声的误差来源，可定义为

(24)

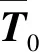
(25)

式(25)等价于求解

(26)

此时，对其进行变换，则Q(λ)可近似表示为

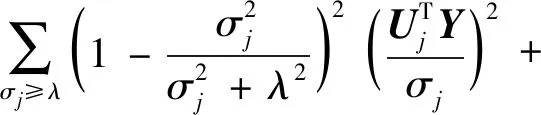
(27)

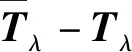
5.2 辐射噪声误差对比

基于Q-O准则分析正常环境下辐射噪声计算误差，声压谱级计算结果对比，如图 6 所示。在全频带上基于Q-O淮则计算得到的声压谱级值与实测值吻合较好，其中：1#工况辐射噪声累计误差为1.58 dB，较L-curve方法降低约0.14 dB；2#工况辐射噪声累计误差为1.40 dB，较L-curve方法降低约0.07 dB。可见，在正常环境下，基于Q-O准则与基于L-curve方法的辐射噪声评估性能相当。

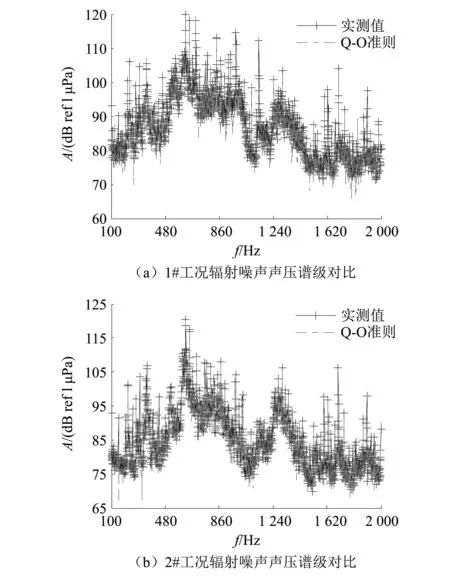
图6 基于Q-O准则计算的辐射噪声声压谱级对比Fig.6 Comparison of radiated noise pressure spectrum levels based on the Q-O criterion

进一步分析基于Q-O准则在不同背景噪声下的辐射噪声计算误差，如表3所示。辐射噪声计算误差随输入响应噪声水平的增大几乎保持不变，而随输出响应噪声水平的增大而增大。其中：1#工况在低噪声水平下辐射噪声计算误差约为 1.90 dB，较L-curve方法降低约0.09 dB，性能基本相同，较SVD方法降低约1.10 dB；在高噪声水平下辐射噪声计算误差约为4.43 dB，较L-curve方法降低约0.42 dB，较SVD方法降低约1.19 dB；2#工况在低噪声水平下辐射噪声计算误差约为 1.99 dB，与L-curve方法性能基本相同，较SVD方法降低约0.71 dB；在高噪声水平下辐射噪声计算误差约为5.17 dB，较L-curve方法降低约0.32 dB，较SVD方法降低约1.17 dB。可见，随着背景扰动的增大，基于Q-O准则方法综合平衡正则化误差与摄动误差，辐射噪声计算误差要低于L-curve方法，反映在高噪声背景环境下，Q-O准则可较L-curve方法计算得到最佳的正则化参数，其环境扰动性能要优于L-curve方法。

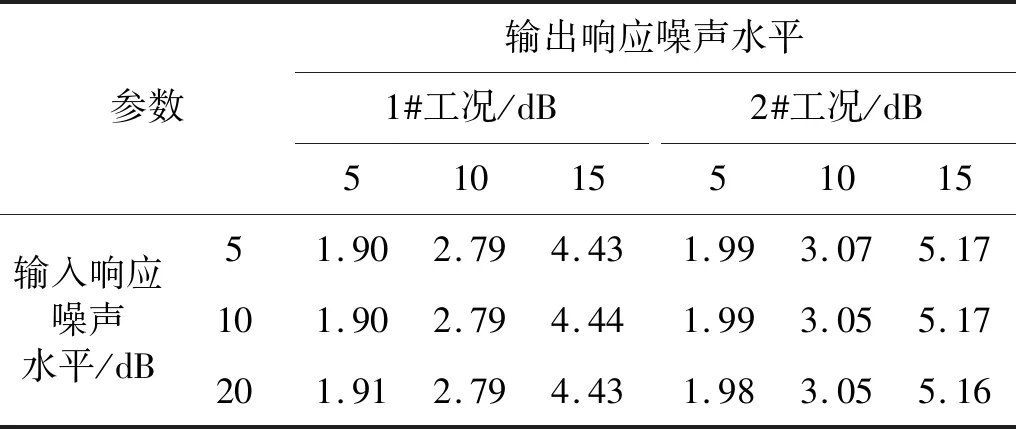
表3 基于Q-O准则的不同环境下辐射噪声累计误差对比Tab.3 Comparison of cumulative errors based on Q-O criterion under various noise levels

5.3 最佳正则化参数变化对辐射噪声误差影响分析

从Q-Q准则等计算得到的不同正则化参数来看，不同的方法皆是致力于计算“最佳”正则化参数，不同的正则化参数导致辐射噪声计算误差也不尽相同。因此，基于Q-O准则计算得到的正则化参数基础上，从改变正则化参数角度，对正则化参数施加不同程度的人为误差，讨论其鲁棒性，即正则化参数波动对辐射噪声计算误差的影响，结果如表4所示。“0 dB”指正常环境，而由于输入响应噪声水平对辐射噪声计算误差无影响，表中仅讨论输出响应中施加不同噪声水平下的辐射噪声计算误差(输入响应中噪声水平为5 dB)；“-10%”表示在最佳正则化参数基础上减小10%，其余与之类似，分别与基于Q-O准则计算得到的辐射噪声结果对比。

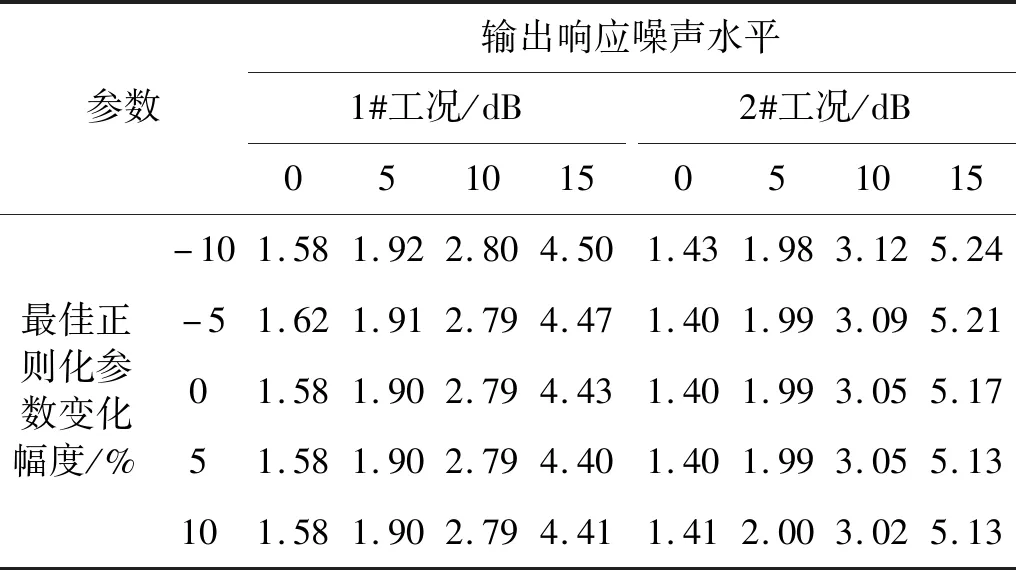
表4 不同正则化参数下辐射噪声累计误差对比Tab.4 Comparison of cumulative errors with various regularization parameters

对于1#工况，在高噪声背景下，其辐射噪声计算误差随正则化参数的增大先减小后增大，在正则化参数增大5%时，辐射噪声计算误差最小，约为4.40 dB，较Q-O准则辐射噪声计算误差降低约0.03 dB，在其余背景噪声或正常环境下，辐射噪声计算误差都不小于基于Q-O准则的辐射噪声计算误差；对于2#工况，在中等噪声背景下，其辐射噪声计算误差随正则化参数的增大而减小，在正则化参数增大10%时，辐射噪声计算误差最小，约为3.02 dB，较Q-O准则辐射噪声计算误差降低约0.05 dB，在高噪声背景下，其辐射噪声计算误差随正则化参数的增大而先减小至不变，在正则化参数增大5%时，辐射噪声计算误差最小，约为5.13 dB，较Q-O准则辐射噪声计算误差降低约0.04 dB，在低背景噪声或正常环境下，辐射噪声计算误差基本不小于基于Q-O准则的辐射噪声误差。

可见，在较高噪声背景下，改变基于Q-O准则计算得到的最佳正则化参数，辐射噪声计算误差会在基于最佳正则化参数得到的误差附近波动，最大可进一步降低误差约0.05 dB，与基于Q-O准则方法计算得到的正则化参数性能基本相同，表明在有限计算下，基于Q-O准则综合考虑计算过程中摄动误差与正则化误差之间的平衡，其计算得到的正则化参数基本可视为最佳正则化参数，在船舶工程应用上可指导优化辐射噪声计算误差。