托盘运输包装单元冲击响应的试验与有限元分析
2021-09-27王志伟
王志伟,伍 炼
(1.暨南大学 包装工程研究所,广东 珠海 519070;2.暨南大学 产品包装与物流广东普通高校重点实验室,广东 珠海 519070;3.暨南大学 珠海市产品包装与物流重点实验室,广东 珠海 519070)
实际物流中,大多数的包装产品都是通过堆码的方式来进行运输。运输过程中,由于路面不平而产生的冲击和振动是引起包装件破损的主要原因[1],所以产品的包装防护设计应考虑振动与冲击的作用[2]。国内外学者做了大量的产品堆码包装方面的研究,但主要集中在产品关键部件的冲击破损[3-6]和复杂运输包装系统振动的分析方法方面[7-8],而在托盘堆码运输单元的冲击响应分析以及有限元建模方面却没有相关的研究。在堆码包装研究方面,主要集中在静态条件下产品受静压以及在动态条件下堆码包装受振动的情况,而堆码包装系统受到瞬态冲击的研究较少[9-13]。
孙君等[14-15]通过随机振动试验分析了堆码啤酒瓶周转箱中不同位置的啤酒瓶的振动特性及加速度峰值分布规律。刘远珍等[16-17]探讨了在堆码包装系统中,高斯信号激励下引起包装系统响应呈现非高斯特性的原因。房树盖等[18]针对不同加速度谱型激励下非线性堆码包装系统的动力学响应进行研究,找到了决定整个非线性系统响应的原因是共振区域的激励。Wang等[19-20]研究了堆码包装系统在不同约束条件、不同振动等级、不同谱型激励下的动压比-频率图、动压力响应功率谱和动压力的力水平穿越分布,给出动压力的力水平穿越分布总体上是接近Weibull分布的结论;同时也研究了堆码包装系统的动压力峰值分布规律,给出了线性系统中非零均值的峰值概率密度函数。在运输包装动力学性能的研究中,基于构件的加速度响应功率谱密度的加速随机振动测试技术[21-22]的提出,丰富了堆码包装系统的试验研究方法。
在产品包装有限元分析(finite element analysis,FEA)方面,主要用于分析冲击与振动情况下的产品性能[23-30],而通过有限元方法对复杂堆码包装系统受冲击时的动态响应的研究较少。林深伟等[31-33]采用试验与有限元分析相结合的方法,得出两层堆码包装系统中上层包装件的加速度功率谱主要受一阶共振频率控制,而下层包装件的加速度功率谱受一阶共振频率和二阶共振频率共同控制。刘龙涛等[34]采用有限元分析软件ANSYS对某机载产品进行了模态分析和随机振动分析,得到了随机振动下的应力响应功率谱。
为防止堆码产品在物流过程中的移动和相互碰撞,通常在运输过程中对堆码包装单元进行不同程度约束,也就是对整体进行捆扎。不同的约束方式,对堆码包装单元的冲击响应特性会产生重要影响,而在托盘堆码运输单元的冲击响应分析这方面至今几乎没有研究。本文以蛋白粉罐托盘运输单元为研究对象,通过试验与有限元相结合的方法研究该运输单元在3种约束方式、不同冲击位置以及两种冲击方向下(水平冲击和竖直冲击)的冲击响应特性;并进一步通过有限元方法分析拉伸缠绕膜加4条打包带约束方式下的冲击力载荷和最大响应位移以及最大响应加速度的关系。
1 材料和系统参数测定
试验用托盘运输单元由马口铁蛋白粉罐、瓦楞纸板衬垫、木质顶板、木托盘、聚丙烯打包带、聚乙烯拉伸缠绕膜组成,每层70个蛋白粉罐,共9层,如图1(a)所示。单层蛋白粉罐的排列方式如图1(b)所示。层与层之间用瓦楞纸板间隔,按层数从底层到顶层进行编号(1~9)。蛋白粉罐为圆柱体结构,内直径为128 mm,高度为175 mm,厚度为0.2 mm。托盘尺寸为1 200 mm×1 000 mm,瓦楞纸板衬垫的厚度为2 mm,打包带的厚度为1 mm,拉伸缠绕膜的厚度为0.02 mm。
(1)拉伸缠绕膜和打包带弹性模量的测定。切取10个150 mm×10 mm的聚乙烯拉伸缠绕膜、10个300 mm×100 mm的聚丙烯打包带试样,采用CMT8202万能材料试验机,以50 mm/min的加载速度对试样进行拉伸性能测试,得到拉伸缠绕膜和打包带的力-位移曲线。通过计算得到拉伸缠绕膜和打包带的弹性模量平均值分别为1.75 MPa和1.66×103MPa。
(2)瓦楞纸板衬垫弹性模量的测定。裁取5个100 mm×100 mm的瓦楞纸板衬垫试样,使用Criterion系列微机控制电子万能试验机,沿试样厚度方向以2 mm/min速度进行压缩试验,得到瓦楞纸板衬垫的力-位移曲线。通过计算得到瓦楞纸板衬垫的平均弹性模量为3.14×102MPa。参考一般的纸质缓冲材料,将瓦楞纸板衬垫的泊松比设为0.3。
(3)拉伸缠绕膜的缠绕力以及打包带的捆扎力的测定。通过拉力计测得拉伸缠绕膜对整个系统产生的缠绕力为51.4 N,打包带对整个系统的捆扎力为80.2 N。
在有限元分析中,蛋白粉罐(产品)取马口铁材料参数,托盘和顶板取同质木材料参数。支撑托盘的基础地板相对于其他材料而言,刚性大,取大值。相关参数如表1所示。

表1 材料参数Tab.1 Material parameters
(4)系统阻尼比以及摩擦因数的测定。将图1(a)所示的产品包装件放置在振动台上,加速度固定在顶层蛋白粉罐的内底面上,如图1(c)所示。进行加速度幅值为0.2g的扫频试验,扫频范围3~200 Hz,扫频速率12 Hz/min,得到蛋白粉罐的传递率曲线。利用半功率带宽法,计算得到该系统的阻尼比范围为0.07~0.08。

图1 托盘运输单元Fig.1 Pallet stacked unit
摩擦因数主要来自于蛋白粉罐与纸板的摩擦,采用KHP-015A数显式摩擦因数实验仪,参考GB/T 22895—2008《纸和纸板 静态和动态摩擦因数的测定 平面法》进行摩擦试验测定。裁取80 mm×200 mm纸板试样6张;测试用的滑块质量为200 g,试验速度2 mm/min。试验结果取6组试验的平均值,得到纸板的静摩擦因数为0.30,动摩擦因数为0.25。
2 冲击试验分析
为保持货物在托盘上的整体性,一般需施加适当的约束形成一整体托盘运输单元。最常见的约束方式有:使用打包带进行捆扎和使用拉伸缠绕膜进行裹包。约束方式对托盘运输单元的冲击响应特性具有一定影响。试验和有限元分析采用的3种约束方式,俯视图如图2所示。分别是拉伸缠绕膜加4条打包带(见图2(a),虚线框表示拉伸缠绕膜),6条打包带无拉伸缠绕膜(见图2(b)),4条打包带无拉伸缠绕膜(见图2(c))。

图2 约束方式Fig.2 The bundling method of impact test
采用DASP-V11大容量数据自动采集和信号处理系统进行冲击试验,应用该系统的测量和分析模块,通过采集力锤的冲击激励信号以及加速度传感器的冲击响应信号进行分析。试验采集的水平冲击和竖直冲击激励信号,如图3所示。

图3 冲击激励信号Fig.3 The shape of impact excitation
2.1 水平冲击试验
水平冲击试验研究3种约束方式下托盘运输单元的水平冲击特性。力锤对托盘1,2,3,4 4个位置分别进行水平冲击,分别得到各层Ai,Bi,Ci,Di(i=1,5,9,i为层数)4个测点的加速度响应,如图4所示。力锤的采样频率为10.24 kHz,加速度传感器的采样频率为640 Hz。

图4 水平冲击Fig.4 Horizontal impact
2.2 竖直冲击试验
竖直冲击试验研究3种约束方式下托盘运输单元的竖直冲击特性。力锤从托盘底部位置1从下往上进行竖直冲击,分别得到各层沿Ai,Bi,Ci,Di(i=1,5,9,i为层数)4个测点的加速度响应,如图5所示。力锤的采样频率为10.24 kHz,加速度传感器的采样频率为1 280 Hz。

图5 竖直冲击Fig.5 Vertical impact
2.3 结果分析
2.3.1 水平冲击试验结果分析
通过水平冲击试验,可得到3种约束方式下托盘1,2,3,4位置激励时各层蛋白粉罐各测点的水平传递函数。由于对称性和同一层各测点测试结果相近,这里仅给出托盘1位置激励时各层蛋白粉罐测点Ai(i=1,5,9)的水平传递函数以及托盘3位置激励时各层蛋白粉罐测点Ci(i=1,5,9)的水平传递函数,如图6和图7所示。图6上半部分图和图7上半部分图为试验结果图,图6下半部分和图7下半部分图为后面的有限元分析结果图。
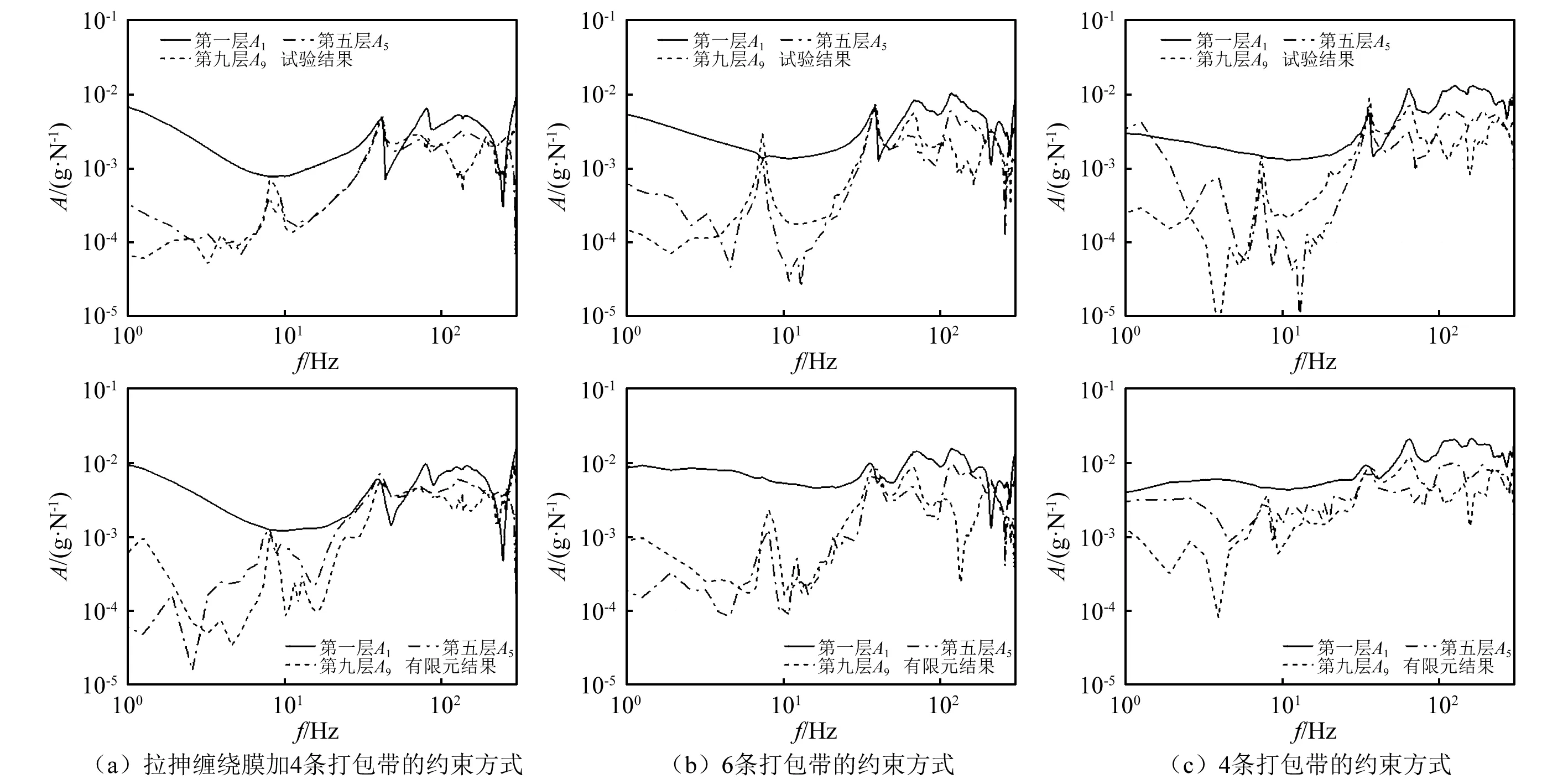
图6 水平冲击传递函数(1号点冲击,Ai点响应)Fig.6 Transfer function of horizontal impact(impact position at point 1,response point at Ai)

图7 水平冲击传递函数(3号点冲击,Ci点响应)Fig.7 Transfer function of horizontal impact(impact position at point 3,response point at Ci)
从图6、图7试验结果图中可以看出:该托盘运输单元具有多个共振点,且在100 Hz以内前三阶共振频率比较明显,前三阶共振频率的特征分别如表2和表3中。从表2和表3中可以看出,拉伸缠绕膜加4条打包带的约束方式下的二阶共振频率和三阶共振频率均大于6条打包带和4条打包带的约束方式。3种约束方式下,系统的二阶和三阶共振频率随着约束方式的加强其而增加大。约束方式的加强引起蛋白粉罐托盘运输单元系统刚度的增大,最终使得系统的共振频率增大。系统的前三阶共振频率在约束方式为6条打包带和4条打包带时相接近,说明这两种约束方式对该系统的影响基本相同,从而在实际运输过程中用4条打包带对其进行捆扎就足够。同时,系统的前三阶共振频率在不同位置(1号点冲击与3号点冲击对比)冲击下相差不大,说明冲击位置的改变对该系统冲击响应的影响甚微,这可能是由于托盘的长宽尺寸相差不大造成的。

表3 水平冲击试验与有限元分析共振频率(3号点冲击,Ci点响应)Tab.3 The resonant frequencies of horizontal impact test and finite element analysis(impact position at point 3,response point at Ci)
2.3.2 竖直冲击试验结果分析
通过竖直冲击试验,可得到3种约束方式下、托盘激励位置在1时各层蛋白粉罐各测点的竖直传递函数。由于同一层各测点测试结果相近,这里仅给出托盘1位置激励时各层蛋白粉罐各测点Ai(i=1,5,9)的竖直传递函数,如图8所示。图8上半部分图为试验结果图,图8下半部分图为后面的有限元分析结果图。
从图8试验结果图中可以看出:该运输包装单元具有多个共振频率,且在100 Hz以内前三阶共振频率比较明显,前三阶共振频率特征如表4所示。由表4可知:系统一阶共振频率在3种约束方式下都在20 Hz左右;二阶和三阶共振频率在约束方式为拉伸缠绕膜和4条打包带情况下均大于其他两种约束方式。同时,6条打包带的约束方式和4条打包带的约束方式在前三阶共振频率时相接近,进一步说明这两种约束方式对该系统的影响相同。

表4 竖直冲击试验与有限元分析共振频率(1号点冲击,Ai点响应)Tab.4 The resonant frequencies of vertical impact test and finite element analysis (impact position at point 1,response point at Ai)

图8 竖直冲击传递函数(1号点冲击,Ai点响应)Fig.8 Transfer function of vertical impact(impact position at point 1,response point at Ai)
3 冲击试验有限元分析
3.1 有限元模型的建立
为实现与试验的相互验证,同时也为了发展物流冲击环境作用下产品包装件复杂结构的分析与设计技术,本文采用有限元分析法分析了托盘运输单元在3种约束方式下的冲击响应特性。在ProE软件中建立三维实体模型,将其导入到Hyper Works软件的LS-DYNA分析模块中建立有限元模型,利用LS-DYNA求解器进行求解。
(1)材料属性设定。在有限元分析中,托盘运输单元的材料参数根据表1进行设置。除此之外,拉伸缠绕膜的缠绕力和打包带的捆扎力参考汽车安全带的处理[35],通过建立预紧力单元对其进行设置,采用100号材料(该材料卡片具有拉伸失效的行为,从而可以模拟拉伸缠绕膜和打包带的实际作用过程),取铁的材料参数(即密度为7.85×103kg/m3,泊松比为0.3,弹性模量为2.00×105MPa)。
(2)单元与网格划分。通过*PART_COMPOSITE,将相同材料属性的结构组成PART便于单元及网格的划分。对于基础地板、托盘、瓦楞纸板衬垫以及顶板设置成实体单元(单元类型为1,即*SECTION_SOLID);将蛋白粉罐设置为壳单元(单元类型为16,即*SECTION_SHELL);将聚乙烯拉伸缠绕膜和聚丙烯打包带设置成膜单元(单元类型为5,即*SECTION_SHELL);将预紧力单元设置成梁单元(单元类型为5,即*SECTION_BEAM)。蛋白粉罐托盘运输单元网格划分,如图9所示。单元数为54 637个,节点数为63 570个。
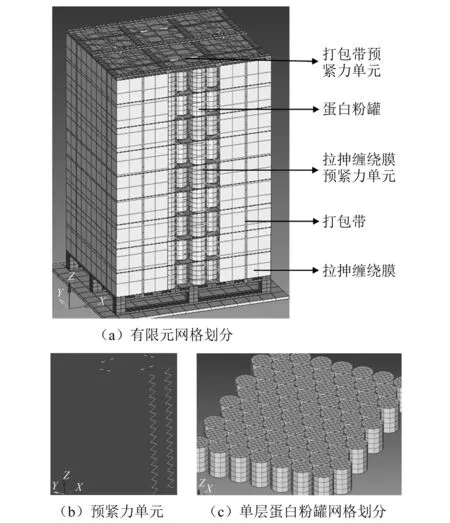
图9 有限元分析模型网格划分Fig.9 The grid of finite element analysis model
(3)接触类型及约束条件设定。考虑产品包装在冲击过程中各部件的实际接触情况,定义托盘底部与基础地板为面面接触,托盘的顶铺板与第一层瓦楞纸板底部为面面接触;预紧力单元与拉伸缠绕膜、预紧力单元与打包带均为点焊接触;其他各部件,蛋白粉罐与上下之间的瓦楞纸板衬垫、蛋白粉罐之间以及顶板与瓦楞纸板衬垫都将其设置为单面自动接触。这里的约束主要是针对水平方向的冲击试验,对底部的基础地板施加x,y,z方向的固定约束。
(4)载荷的施加。载荷的定义由两部分组成:一部分为收缩缠绕膜的缠绕力和打包带的捆扎力的施加;另一部分为冲击激励的施加。拉伸缠绕膜的缠绕力和打包带的捆扎力则通过*INITIAL_AXIAL_FORCE_BEAM卡片将拉伸缠绕膜的缠绕力设为51.4 N,将打包带的捆扎力设为80.2 N。冲击激励主要来自于冲击试验采集到的冲击力锤的激励,将这个作为有限元分析中激励的输入,冲击激励的形状如图2所示。由于在试验过程中是通过力锤冲击托盘来进行冲击试验,所以在有限元分析中,激励的施加是通过节点力(即*LOAD_NODE_POINT(FORCES)卡片)的方式施加给整个系统的。设置系统阻尼参数为0.07,静摩擦因数为0.30,动摩擦因数为0.25。
3.2 有限元结果分析
有限元得到的托盘运输单元的水平冲击加速度响应画在图6有限元结果图、图7有限元结果图中,竖直冲击加速度响应画在图8有限元结果图中;有限元分析得到3种约束方式下的共振频率分别列在表2、表3和表4中。有限元计算得到的共振频率与试验结果吻合较好,有限元得到的蛋白粉罐的传递函数趋势与试验结果一致,能够较好地反映产品包装件的冲击振动特性。在对冲击试验进行分析时,借助有限元分析这样一种手段能够减少成本,同时也能够为堆码包装件系统的分析与设计提供有效手段。
3.3 冲击力与最大响应位移以及最大响应加速度的关系
为进一步探究冲击力载荷与最大响应位移以及最大响应加速度的关系,取水平方向冲击下的拉伸缠绕膜加4条打包带的有限元模型进行分析。在HYPERMESH的LS-DYNA接口中对托盘底部的节点(节点编号为2705)施加X方向的冲击力载荷,冲击力载荷的形状,如图10所示。选取的冲击力载荷的等级分别为196 N,392 N,490 N,980 N,1 470 N,1 960 N,2 450 N,2 940 N,3 430 N,3 920 N,4 410 N,4 900 N。

图10 冲击力载荷的形状Fig.10 The shape of impact load force
取第九层的某一个蛋白粉罐上的节点(节点编号为666832)作为位移和加速度响应的输出节点,得到的最大响应位移以及最大响应加速度结果,如图11所示。其中:图11(a)表示冲击力与最大位移的关系;图11(b)表示冲击力与最大加速度的关系。

图11 冲击力与最大响应位移以及最大响应加速度的关系Fig.11 The relationship between impact load force and maximum response displacement and maximum response acceleration
从图11中可知:随着冲击力载荷的增大,最大位移也随之增大。而随着冲击力载荷的增大,最大加速度响应也随之增大,并且呈现出非线性关系。这是由于蛋白粉罐在受到冲击力载荷的时候发生了从静摩擦到动摩擦的转变。
4 结 论
本文通过试验与有限元相结合的方法,分析约束方式、冲击位置以及冲击方向(水平冲击和竖直冲击)对九层蛋白粉罐托盘运输单元冲击响应特性的影响规律,主要得出以下结论。
(1)水平冲击试验与竖直冲击试验的传递函数表明:该托盘运输单元具有多个共振点,在100 Hz以内主要由前三阶共振频率控制;拉伸缠绕膜加4条打包带的约束方式下的二阶共振频率和三阶共振频率均大于6条打包带和4条打包带的约束方式,而6条打包带的约束方式和4条打包带的约束方式在前三阶共振频率时相接近;说明拉伸缠绕膜加4条打包带的约束方式对该系统的共振频率影响较大。
(2)水平冲击试验表明:该托盘运输单元的前三阶共振频率在不同位置(1号点冲击与3号点冲击对比)冲击下相差不大,说明冲击位置的改变对该系统冲击响应的影响不大;约束方式加强后托盘运输单元二阶共振频率和三阶共振频率有所增加。在只有4条打包带的约束方式下,二阶共振频率为31.87Hz,三阶共振频率为55.62 Hz;在6条打包带约束方式下,二阶共振频率为34.37 Hz,三阶共振频率为59.73 Hz;在拉伸缠绕膜加4条打包带的约束方式下,二阶共振频率为37.50 Hz,三阶共振频率为70.62 Hz。
(3)竖直冲击试验结果表明:系统一阶共振频率在3种约束方式下都在20 Hz左右,说明3种约束方式对一阶共振频率没有影响;二阶和三阶共振频率在约束方式为拉伸缠绕膜和4条打包带情况下均大于其他两种约束方式。
(4)有限元计算得到的共振频率和产品传递函数曲线的趋势与试验结果较好吻合,表明有限元法可为物流中复杂产品包装件的分析与设计提供有效手段。同时,由于摩擦力的存在,冲击力载荷与最大响应位移与最大响应加速度呈现非线性关系。
