基于量子粒子群算法的主动悬架分数阶控制策略
2021-09-27曹青松张定军
许 力,曹青松,张定军
(江西科技学院 机械工程学院,南昌 330098)
主动悬架可以简单看成由被动悬架与作动器组成的一种新型悬架,作动器可实时依据路面信息及车身振动情况按照控制规律对车身产生一个力的作用,来平衡路面的冲击,提高车辆平顺性与乘坐舒适性。所以,作动器控制策略影响着主动悬架性能,相关研究也受到国内外许多学者的广泛关注,已经提出了以整数阶微积分理论作为基础的主动悬架滑模控制、自适应控制、模糊控制等诸多控制策略[1-3]。
近年来,由于分数阶微积分的记忆特性,能更真实地描述具有黏弹、滞回等非线性物体的数学模型,越来越多地应用于磁流变液或油气主动悬架的数学建模上[4-5]。孙会来等[6]采用Caputo分数阶微积分对油气悬架进行数学建模,通过试验证明了分数阶模型比整数阶模型更为精确。此外,分数阶微积分对被控对象参数的变化具有较强鲁棒性等优点[7-8],许多学者将分数阶微积分理论应用于主动悬架的控制器设计。Tar等[9]基于包含空气弹簧、黏性阻尼弹簧和液压非线性阻尼器的模型,引入分数阶控制器以抑制路面带来的振荡。梁军等[10]将其应用于半主动悬架的天棚控制中,对天棚阻尼系数进行优化,提高了平顺性。高远等[11]提出一种以分数阶微分信号作为控制器输入的分数阶模糊控制方法。陈炎冬等[12]在主动悬架滑模控制中引入分数阶趋近率,有效削弱了滑模控制中抖振问题。
在分数阶控制器设计过程中,由于增加了积分阶次或微分阶次等参数,从而使控制器参数整定变得更加复杂。许多学者为简化参数整定过程,将分数阶微积分进行等效逼近[13]再采用各类数字算法对其参数进行优选。Dong等[14]基于电液悬架线性模型,设计了分数阶PIλDμ控制器,采用克隆选择算法对参数进行整定。吴光强等[15]采用Oustaloup滤波器算法对分数阶天棚阻尼半主动悬架进行参数整定,与被动悬架、整数阶主动悬架对比分析。陈炎冬等[16]采用遗传算法对主动悬架分数阶控制器参数进行优化,通过仿真表明,其对削弱车身共振效果明显优于整数阶PID控制器。游浩等[17]针对1/4车辆被动悬架,建立分数阶数学模型,采用粒子群算(particle swarm optimization,PSO)法对弹簧刚度和阻尼系数进行优化,优化后乘车舒适性可明显改善。张欣等[18]针对高低温试验箱分数阶被控系统,设计一个分数阶PIλDμ闭环控制器,利用量子粒子群算法(quantum particle swarm optimization,QPSO)对控制器参数进行整定,采用量子旋转门对粒子位置进行更新,并与PSO整定方法比较,得出QPSO具有更强的寻优能力。
本文基于上述研究背景,建立基于分数阶PIλDμ控制器的1/4悬架模型,采用QPSO算法对PIλDμ进行参数整定,建立集合车身垂向加速度、悬架动挠度和车轮动载荷的综合评价函数,从时域和频域分析被动悬架、整数阶主动悬架和分数阶主动悬架的控制性能。
1 分数阶微积分与Outstaloup逼近法
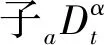
(1)
由式(1)可知,分数阶微积分算子sα的幅频特性曲线是以20αdB/dec为斜率的直线,相频特性为恒定值α·(π/2)。整数阶微积分中α只能为正整数或负整数,幅频和相频相对固定、不易调节,分数阶微积分中α可以为任意实数,幅频和相频特性调节更为方便。
关于分数阶微积分的数值计算,不同的定义式有不同的计算方法,通常计算结果受步长h影响较大。要更准确地计算其数值,h值越小越好,累加次数相应增多,计算量更大。将分数阶微积分分成几个频率段,并在各频率段内用不同阶次的整数阶微积分进行拟合近似,可得到较为准确的计算结果,且减小了累加次数。本文采用的是改进型Outstaloup逼近算法,在某一频率段(ωb,ωh)内对分数阶微积分算子sα可近似为整数阶零极点型式的累乘。
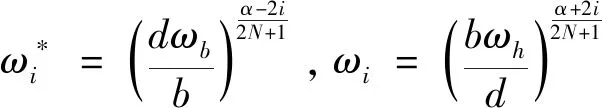
在频率段(0.001 rad/s,1 000 rad/s)内,-0.5阶微分算子伯德图在滤波器阶次分别为1,3,5时的曲线,如图1所示。滤波器阶次越高,逼近效果越好,但是增加了累乘次数,所以本文选取的滤波器阶次N为3。
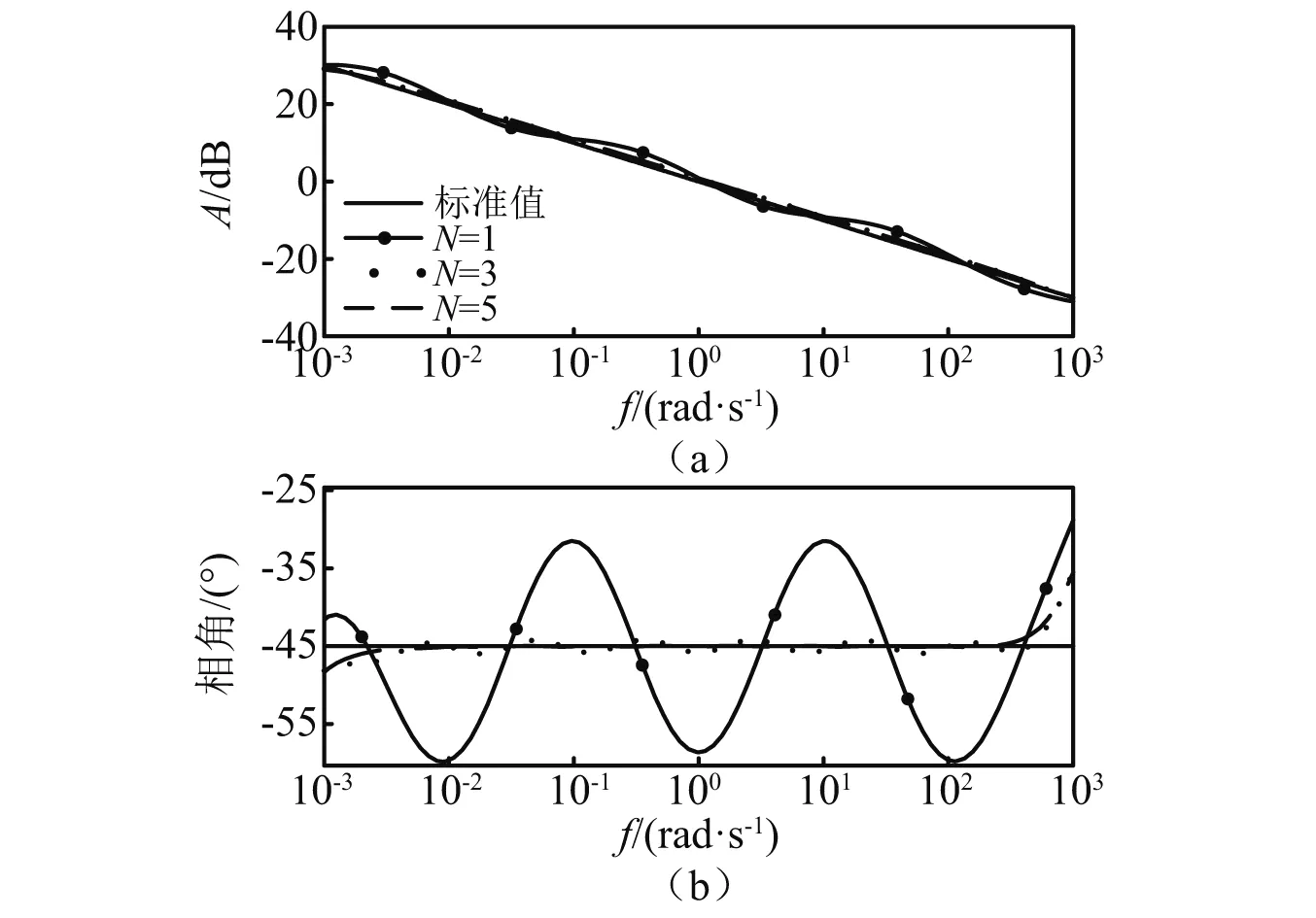
图1 不同阶次滤波器逼近效果Fig.1 Approximation effect of different order filters
2 基于分数阶控制器的主动悬架模型
2.1 1/4车辆主动悬架模型
图2所示为1/4悬架振动模型,忽略了轮胎阻尼,图中:mb为车身质量,mt为轮胎质量,kb为车身悬架刚度,cb为悬架阻尼系数,xb,xt分别为车身和轮胎的垂向位移,x0为路面输入,u为作动器输出的力。那么,主动悬架系统的线性动力学微分方程为
(3)
2.2 基于分数阶PIλDμ控制器的悬架模型
图2中u是由车身加速度误差信号经PIλDμ控制器得到,如式(4)所示
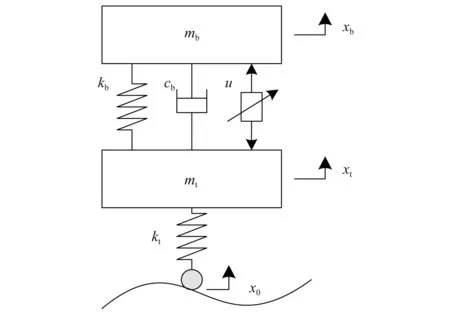
图2 主动悬架系统模型Fig.2 Active suspension system model
U(s)=-F(s)s2Xb
(4)
对式(3)两边做拉普拉斯变换,可得车身位移和轮胎位移对路面激励的传递函数,分别如下所示
(5)
(6)
式中:A(s)=s2[F(s)+mb]+B(s);B(s)=cbs+kb。
同时,分数阶控制器PIλDμ是在整数阶PID控制器的比例系数、积分系数、微分系数3个可调参数基础上,再引入可调的积分阶次参数λ和微分阶次参数μ,其能灵活地调节控制器。分数阶PIλDμ控制器的时域表达式为
(7)
其传递函数为
F(s)=kp+kis-λ+kdsμ
(8)
当F(s)=0时,为被动悬架;当F(s)=kp+kis-1+kds时,为含整数阶PID控制器的主动悬架;当式(4)中的F(s)为式(8)时,则为含分数阶PID控制器的主动悬架。因此,可设计如图3所示含分数阶PID控制器的主动悬架控制系统。
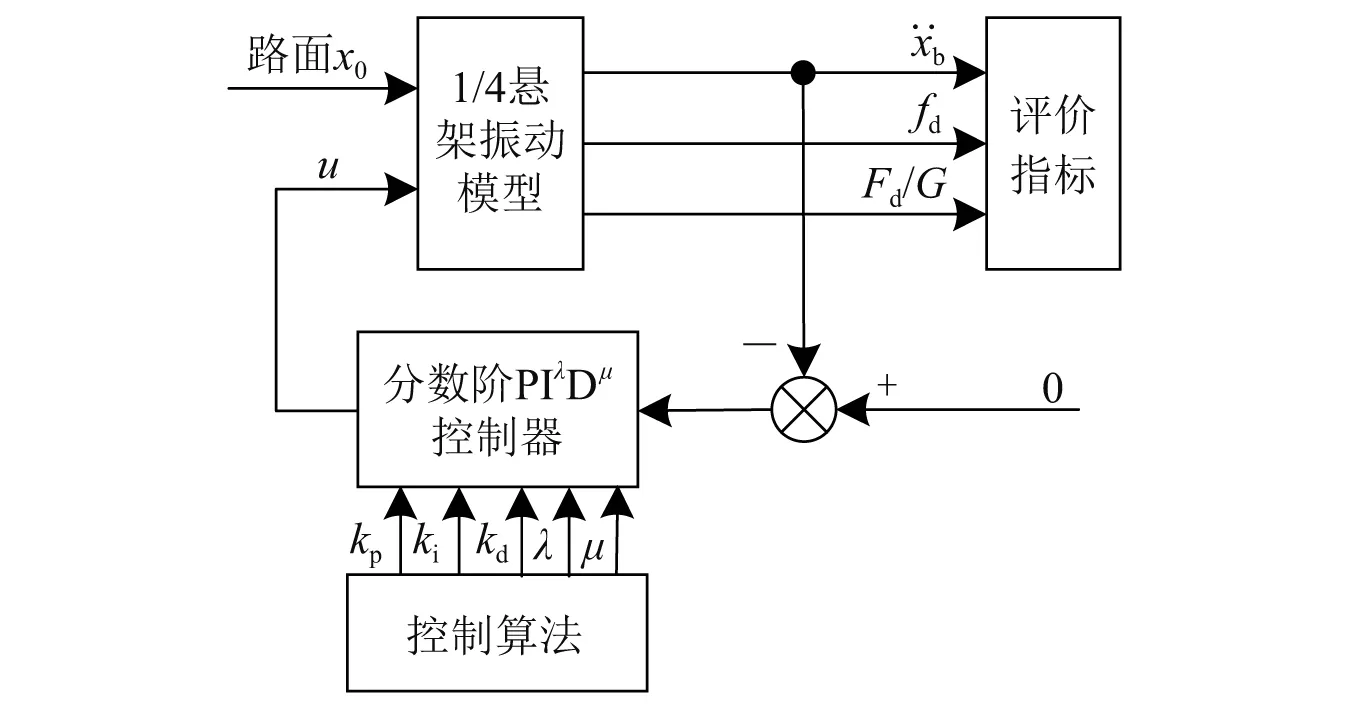
图3 系统控制框图Fig.3 System control block diagram
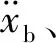
(9)
式中:g为重力加速度,取9.8 m/s2;fd_max为悬架动行程最大值,取0.1 m;l1,l2,l3为加权系数,定义域均为(0,1),三者之和为1,根据主动悬架不同性能的需要而设置加权系数大小。
3 主动悬架分数阶PIλDμ参数量子粒子群优化
3.1 量子粒子群优化算法(QPSO)
QPSO算法是一种具有全局搜索能力的智能算法,解决了PSO算法容易陷入局部最优解的问题。在粒子进化时,群体中的大部分粒子可能聚集在次优解附近,只有少部分粒子远离次优解,为了避免粒子过早向次优解聚集而引起的早熟现象,本文引入群体平均最佳粒子作为粒子进化因素之一,这样可使远离次优解的粒子做全局搜索,找到最优解。
将[Kp,Ki,Kd,λ,μ]看成五维解空间中粒子,并找出使主动悬架的评价函数值最小的粒子,这些粒子具有量子特性,随迭代次数的增加而进化。每次进化,粒子依据个体最佳粒子Pi(t)、群体最佳粒子G(t)、群体平均最佳粒子C(t)以及随机函数组合成的进化规则而进行更新。C(t)可防止群体陷于早熟,随机函数使得粒子能以不同的概率出现在解空间各个位置,降低了局部最优可能性。其进化规则如下式所示
Xi,j(t+1)=±α·|Cj(t)-Xi,j(t)|·ln[1/ui,j(t)]+
si,j(t)
(10)
其中,
si,j(t)=φi,j(t)·Pi,j(t)+[1-φi,j(t)]·Gj(t)
(11)
(12)
式中:t为第t次迭代;Xi,j为第i粒子第j维;α为收缩-扩张系数,令其由首次迭代时为1并线性衰减至迭代结束时为0.5;ui,j(t),φi,j(t)为第t次迭代第i粒子第j维的概率函数,且ui,j(t),φi,j(t)~U(0,1);Pi,j为第i粒子的个体最佳粒子的第j维;Gj为粒子群最佳粒子的第j维;Cj为粒子群平均最佳粒子的第j维;M为粒子群粒子个数。
3.2 主动悬架分数阶控制器参数优化与确定
根据3.1节QPSO算法的思想,主动悬架分数阶控制器参数具体整定流程图如图4所示。
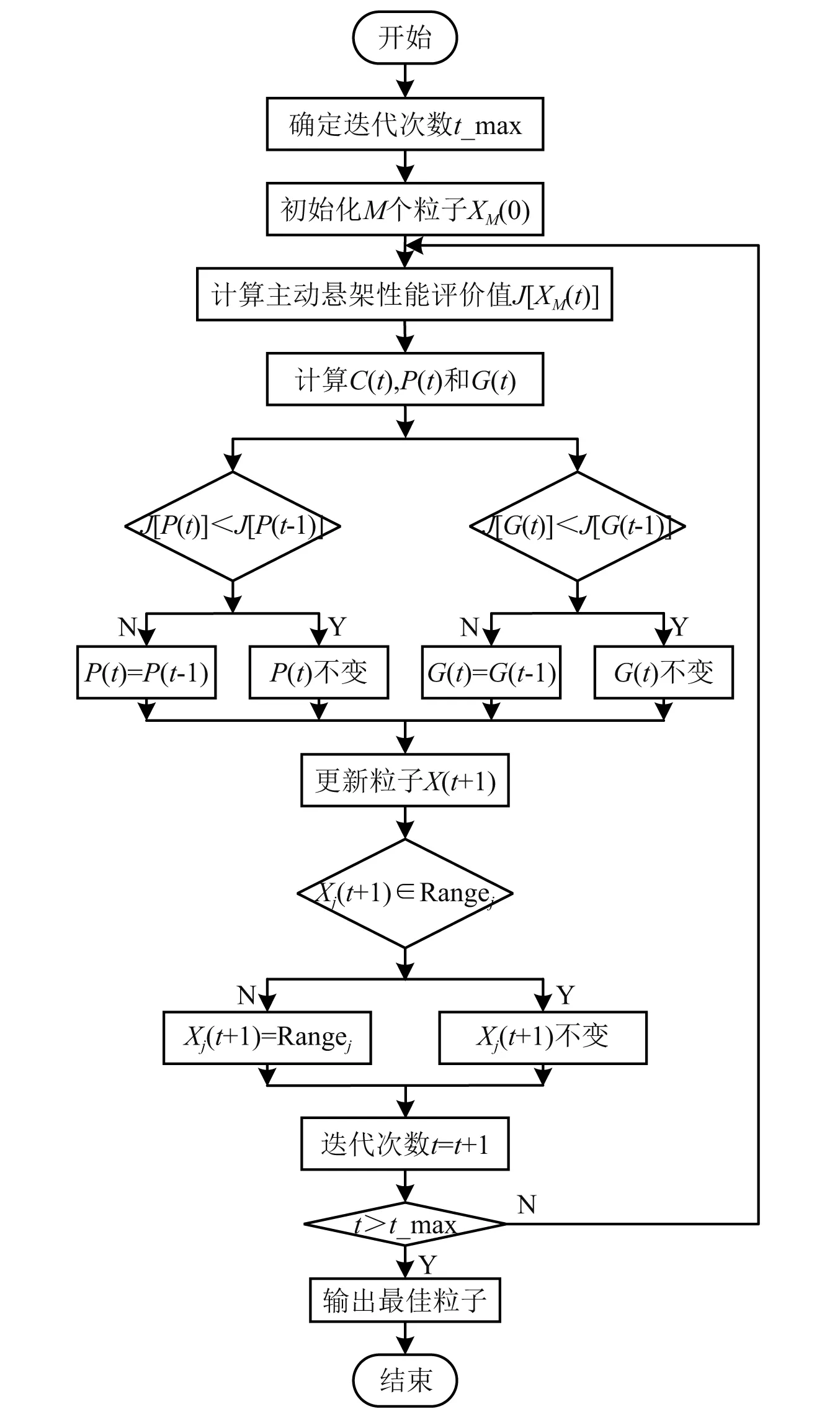
图4 QPSO参数整定流程图Fig.4 Flow chat of setting parameters by QPSO
步骤1初始化,设置迭代次数t_max及粒子初始值。将控制器参数[Kp,Ki,Kd,λ,μ]看成五维空间中粒子,在其取值区间内随机生成M个粒子当作初始值,并且此M个粒子看成首次迭代中的个体最佳粒子Pi(0)。
步骤2将步骤1生成的各粒子代入式(5)、式(6),得到车身垂向加速度、悬架动挠度和车轮相对动载荷值,并将这3个值代入式(9)得到各粒子对应的综合评价值J[Xi(0)]。找到M个粒子中评价值最小的那个粒子记为G(0)。同时,计算M个粒子的平均值C(0)。利用式(10)~式(12)获得M个新粒子XM(1)。
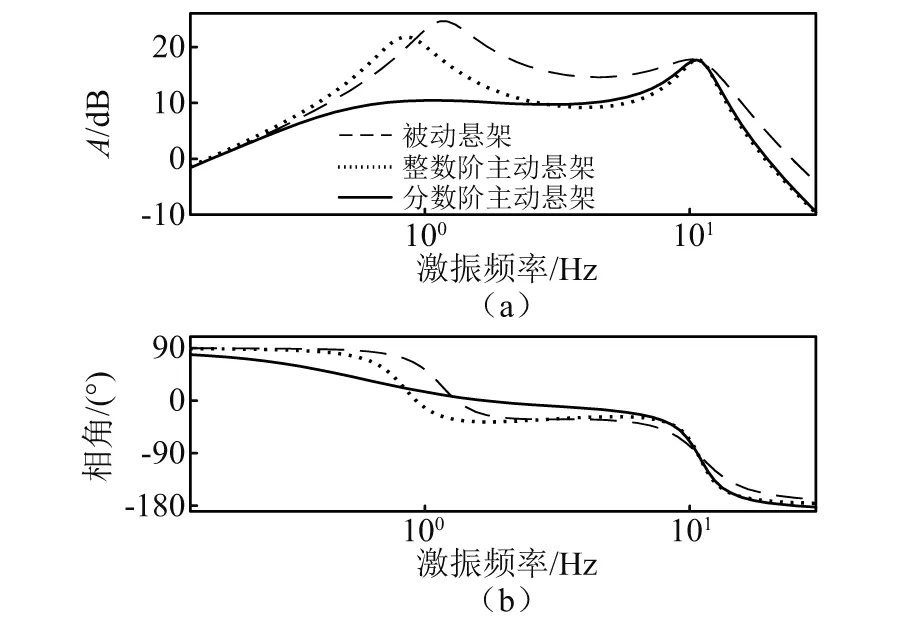
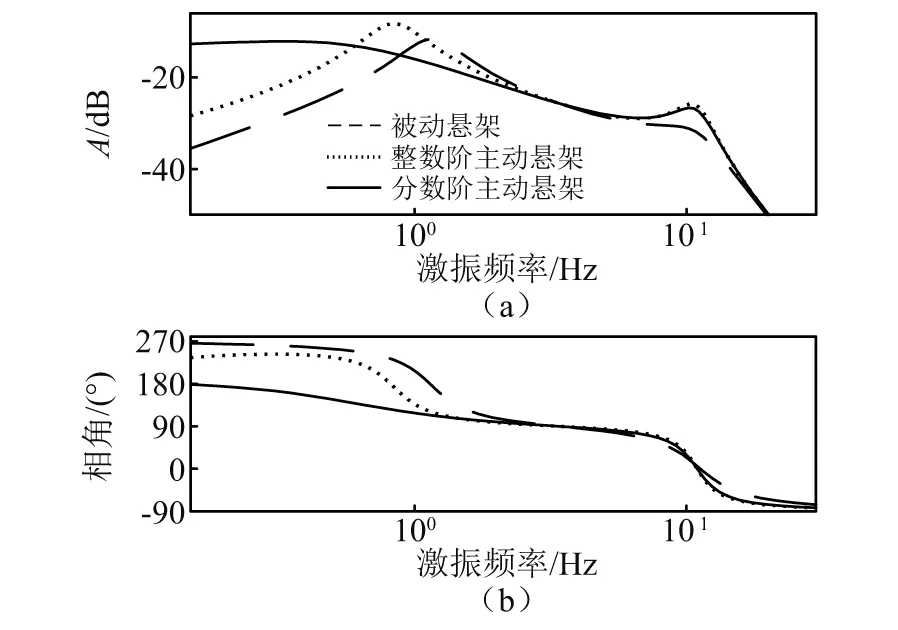
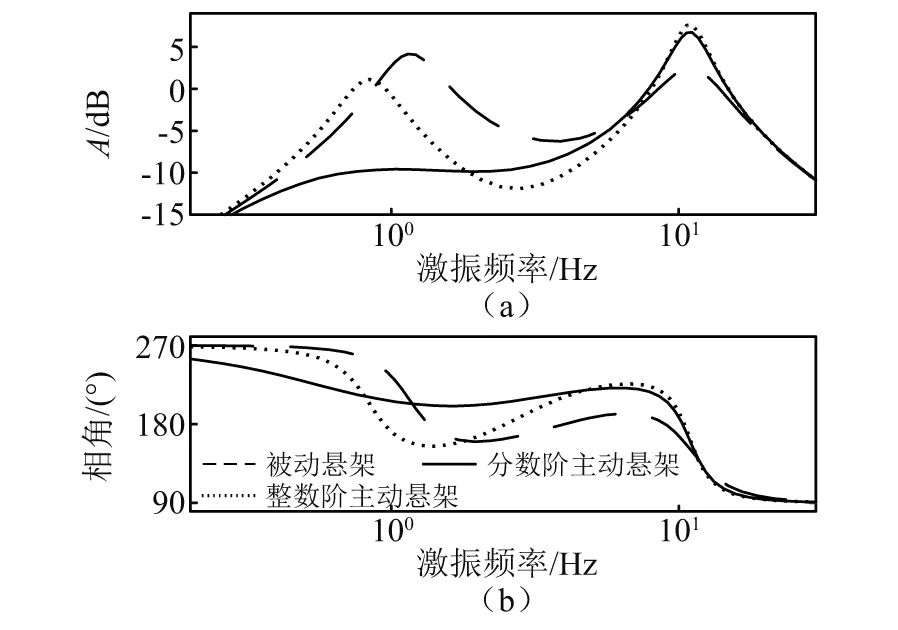
步骤3计算粒子更新后的综合评价值,找出本次迭代最佳粒子G(t)(综合评价值小者为佳),并判断J[G(t)] 步骤4找出本次迭代每个个体最佳粒子Pi(t),判断方法与步骤3一致,并计算出的平均最佳粒子C(t)。 步骤5根据式(10)~式(12)更新出下次迭代的所有粒子XM(t+1),并判断新粒子各维是否超出边界Range,若超出,则用边界值代替那一维,否则,粒子值不变。回到步骤3。 步骤6迭代结束,输出所有迭代过程所有粒子中使悬架综合评价指标值最小的那个粒子。 悬架系统参数如表1所示。设定式(8)中加权系数为:l1=0.8,l2=0.1,l3=0.1。依据3.2节的算法,设定t_max=100,M=50,Kp∈(-1 000,1 000),λ∈(-1,0),μ∈(0,1),Ki,Kd∈(-5 000,5 000)。路面输入为采用滤波白噪声法生成的车速为30 km/h的B级路面随机激励信号,其时域曲线如图5所示。 表1 悬架参数Tab.1 Suspension parameters 图5 路面激励Fig.5 Road excitation 图6所示为两种主动悬架参数整定过程,相比于QPSO整数阶参数整定,对分数阶参数进行整定时,J值更小并更容易收敛至最优值,全体粒子也更容易达到最佳位置。说明虽然分数阶参数比整数解参数多了两个,但利用QPSO对分数阶参数整定时,效率更高。 图6 参数整定过程Fig.6 Parameters setting process 求得整数阶控制器参数为:[334.5,362.9,0],分数阶控制器参数为:[54.39,3 750,69.59,-0.887 3,0.273 5]。 对被动悬架、整数阶主动悬架和分数阶主动悬架进行时域仿真分析,观测车身垂向加速度、悬架动挠度及车轮相对动载荷的变化趋势。表2为3个观测参数的均方根值,图7~图9为观测参数时域曲线,图10为两种主动悬架作动器输出的作用力时域曲线。 表2 被测参数均方根值Tab.2 RMS of measured parameters 见表2所示,相比于被动悬架,整数阶控制方式及分数阶控制方式下的主动悬架综合性能分别提升了21.64%和27.11%。车身垂向加速度降低明显,其中整数阶主动悬架下降了28.56%,分数阶主动悬架降低了30.8%。结合图7,分数阶主动悬架的瞬时值相对最小,被动悬架的瞬时值相对最高。所以由QPSO确定参数的两种主动悬架均可减小车身垂向加速度,提升车辆平顺性,并且分数阶主动悬架相对整数阶主动悬架提升的更明显。 图7 车身垂向加速度时域曲线Fig.7 Vertical acceleration of vehicle body 在悬架动挠度方面,表2所示的被动悬架均方根值最小,而分数阶主动悬架相对最大,但与整数阶主动悬架相差不多。结合图8可知:分数阶悬架动挠度的最大值与整数阶主动悬架相比有所下降,相比被动悬架其最大值几乎相等,均在0.016 m附近。在车轮相对动载荷上,被动悬架也是表现最为良好的。结合表2和图9可知:无论是均方根值还是瞬时值,分数阶主动悬架均优于整数阶主动悬架。总体来看:分数阶主动悬架相比整数阶主动悬架能够进一步增强车辆的减振性能,提升了平顺性。 图8 悬架动挠度时域曲线Fig.8 Dynamic deflection of suspension 图9 车轮相对动载荷时域曲线Fig.9 Wheel relative dynamic load 图10为两种主动悬架控制力的输出曲线,整数阶控制力均方根值为96.67 N,均方根值为108.1 N。分数阶控制的作动器相比整数阶控制在增加汽车平顺性同时,加大了作动器的输出。然而,相对于分数阶控制的输出,整数阶作动器在相同时间内,正负变化相对频繁。 图10 作动器输出Fig.10 Actuator output 根据式(5)、式(6)可求出车身垂向加速度、悬架动挠度和车轮-路面相对动位移对路面激励导数的传递函数。其伯德图如图11、图12、图13所示。 图对频域特性Fig.11 Frequency-domain 图12 xb-xt对频域特性Fig.12 Frequency-domain characteristics of xb-xt versus 图13 Fd/G对频域特性Fig.13 Frequency-domain characteristics of Fd/G versus 由1/4车辆悬架的频率特性可知:该模型有两个共振点,分别处在1 Hz和10 Hz附近。由图11可知:在1 Hz附近的共振点处,整数阶和分数阶控制的主动悬架相对被动悬架,其增益峰值分别减小了35%和69%,主动悬架对1 Hz处的共振有明显抑制作用,但分数阶的抑制效果更好,从而对车辆平顺性有显著改善。在3~10 Hz的频率段,主动悬架的增益幅值明显下降,并且两种主动悬架对振动的抑制效果相差不大。在10 Hz及以上的频率段内,两种主动悬架对于平顺性的改善效果不明显。 由图12可知:整数阶主动悬架动挠度的增益在模型的两个共振点处均保持较大值,分数阶主动悬架在4 Hz以下的频段内对悬架动挠度的增益最低,而在4 Hz以上频段内,其增益相较于被动悬架恶化。 由图13可知:在1 Hz左右的频段内,分数阶主动悬架车轮相对动载荷增益最低,在中间频段整数阶主动悬架增益最低,在10 Hz左右的频段内,两个主动悬架对车轮相对动载荷有明显的恶化,这是因为评价指标的制约,相较而言,整数阶主动悬架的恶化程度高于分数阶主动悬架。综合以上幅频分析可知,分数阶控制主动悬架对于低频段减小共振效果明显。 从图11~图13相位曲线来看:含分数阶控制器的主动悬架系统低频段相位变化更加平缓,高频段相位变化与整数阶主动悬架和被动悬架变化趋势类似,分数阶控制器更容易实现主动悬架控制系统的稳定性。 建立1/4主动悬架振动模型,采用量子粒子群优化算法对整数阶控制器和分数阶控制器进行参数整定,从时域、频域两方面对被动悬架、整数阶主动悬架和分数阶主动悬架进行对比研究。结果表明,主动悬架对车辆平顺性有很大改善,相对于整数阶主动悬架,分数阶主动悬架在车身垂向加速度、悬架动挠度和车轮动载荷等指标方面均有一定程度的改善;相比被动悬架在高频段有一定程度恶化,而低频段分数阶主动悬架性能改善明显。因此,采用量子粒子群算法对含分数阶控制器的主动悬架进行参数优化的方法可取,为主动悬架分数阶控制器设计奠定基础。4 仿真分析
4.1 仿真参数
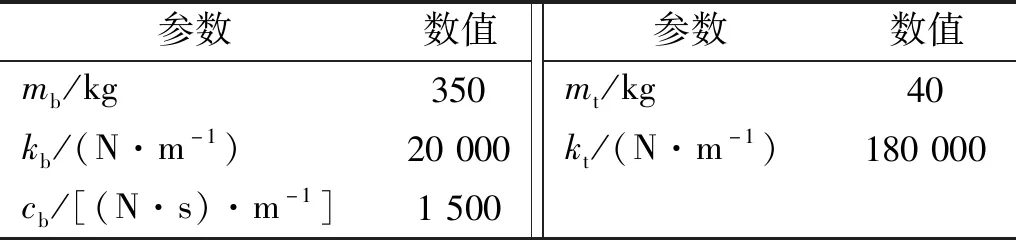
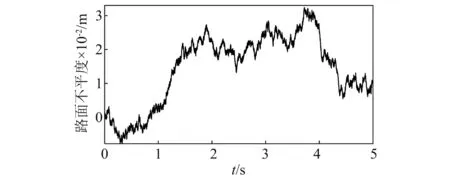
4.2 控制器参数整定过程
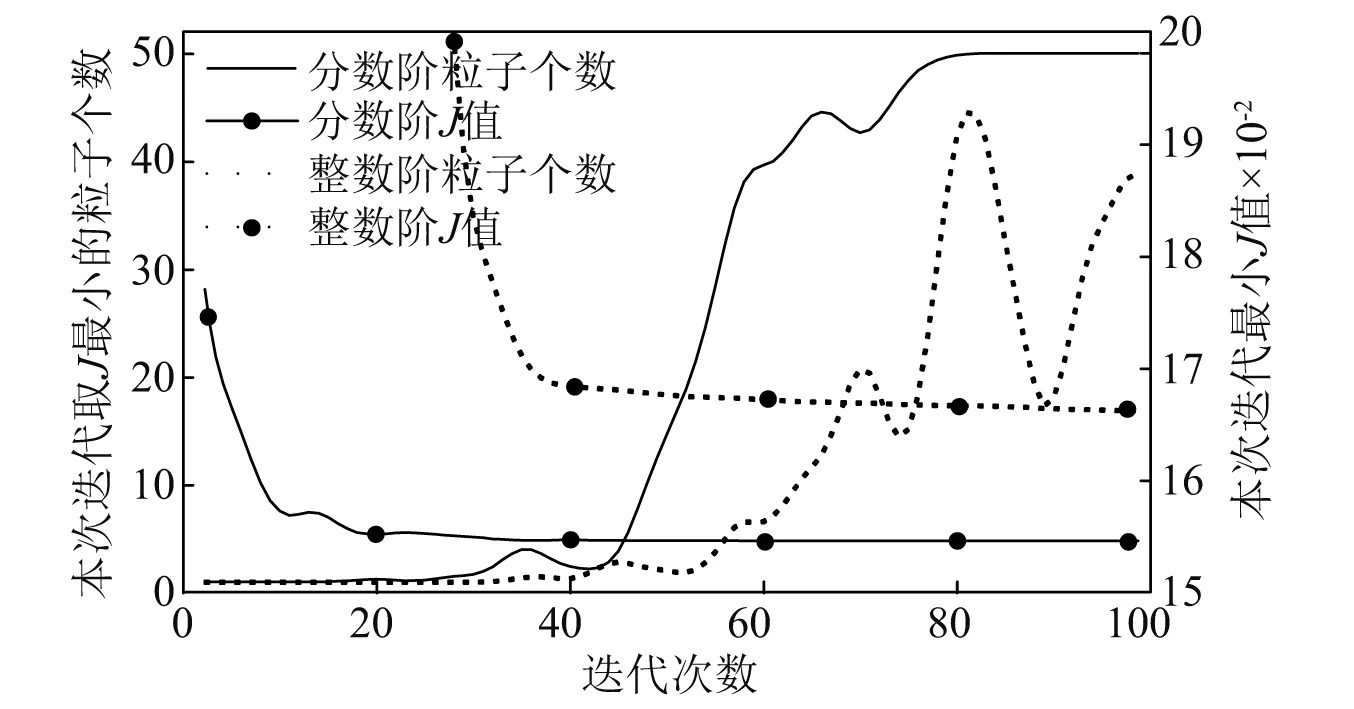
4.3 时域分析
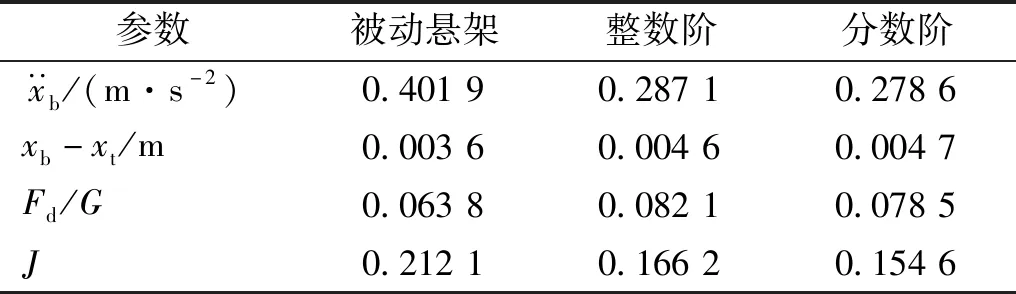
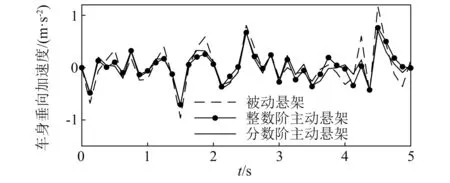
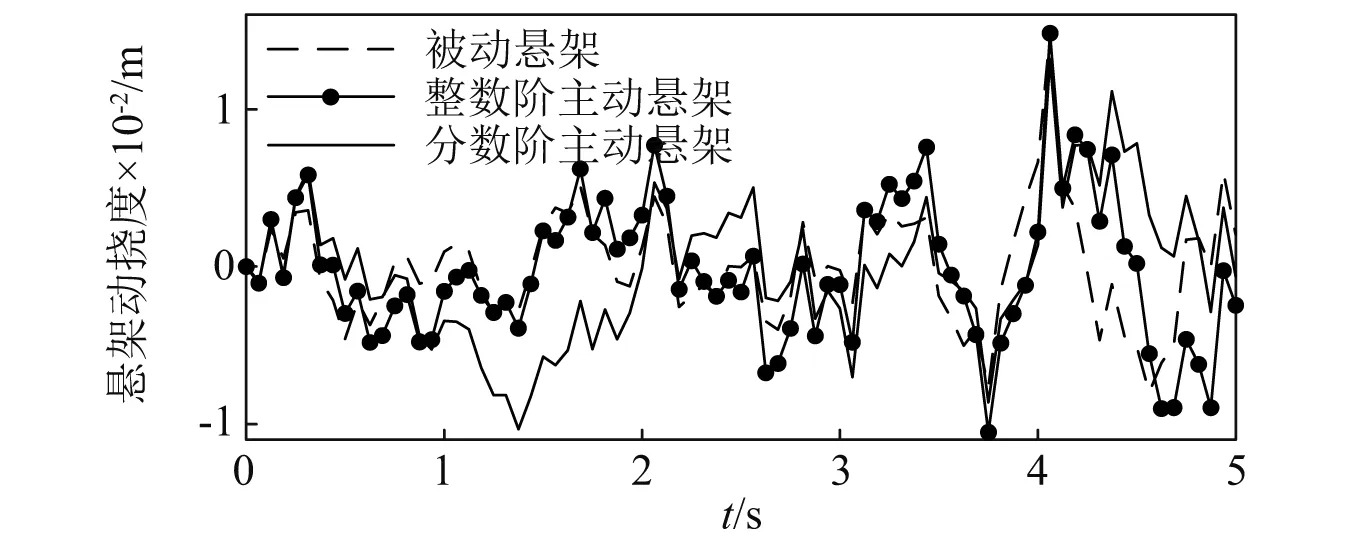
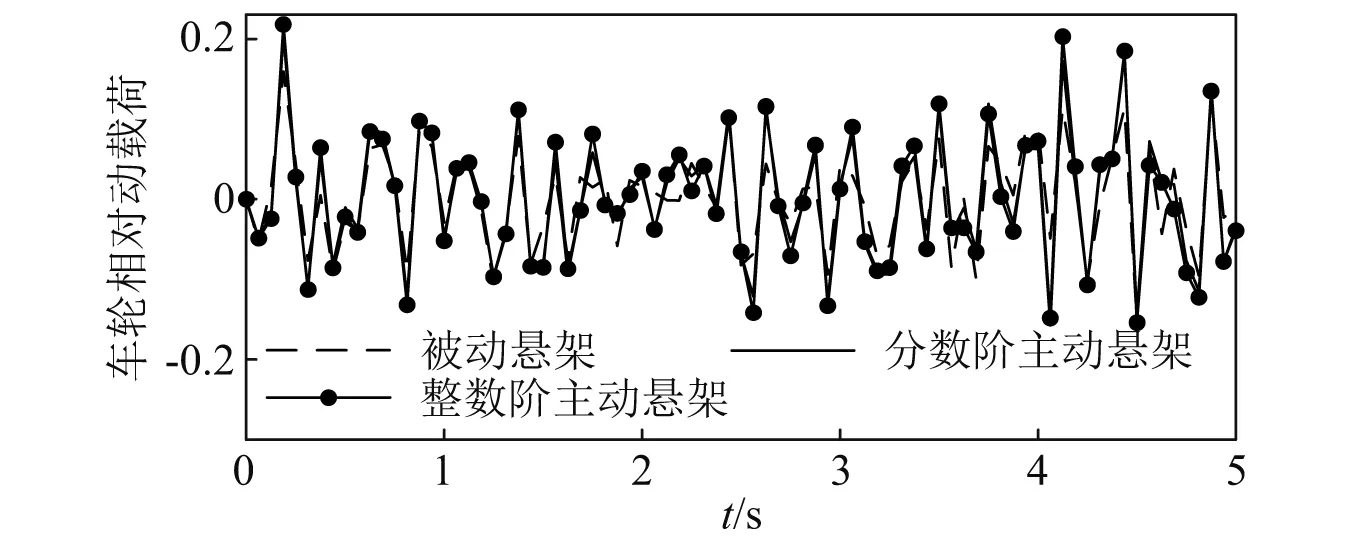
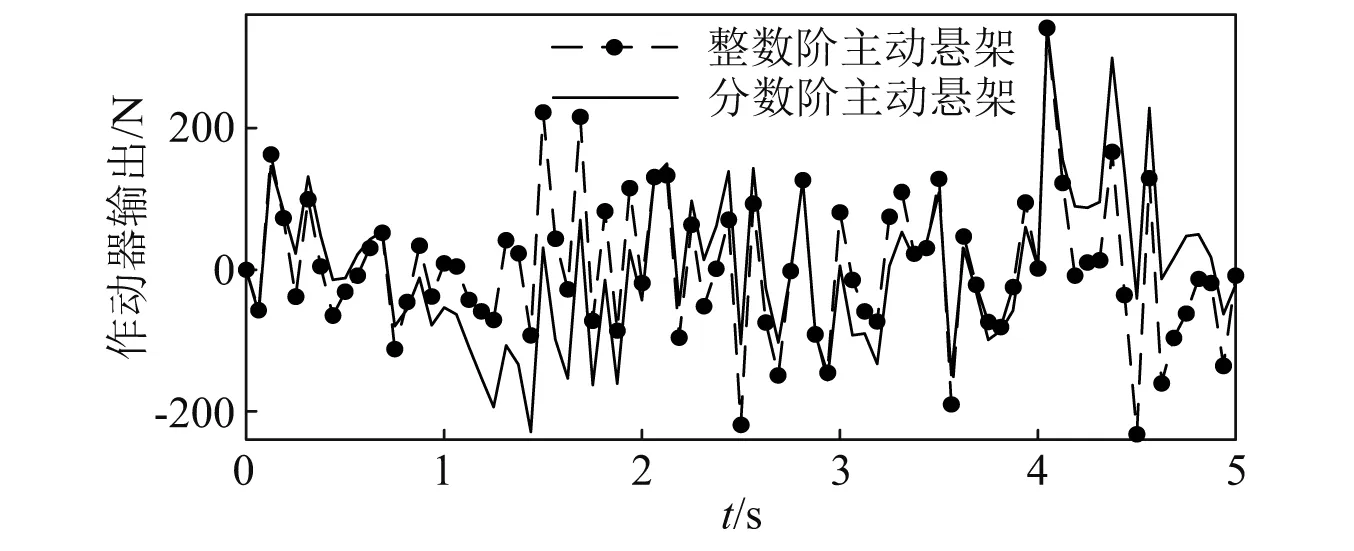
4.4 频域特性分析
5 结 论
