钢弹簧浮置板隔振器垂向动反力随机振动特征研究

朱志辉，黄宇佳，黄承志，丁德云

(1.中南大学 土木工程学院，长沙 410075；2.中南大学 高速铁路建造技术国家工程实验室，长沙410075；3.北京九州一轨环境科技股份有限公司，北京 102600)

我国轨道交通正在迅猛发展，为减少城市轨道交通对线路沿线造成的振动与噪声影响，工程中常采用钢弹簧浮置板轨道(floating slab track，FST)。钢弹簧隔振器是钢弹簧浮置板轨道的重要元件，钢弹簧隔振器动反力(dynamic reaction force,DRF)是引起基础动力响应的激振力，直接反映了浮置板轨道的减振性能。钢弹簧隔振器受力情况复杂，极易出现损坏现象，因此针对钢弹簧隔振器的研究成为近年来最热门的问题之一。目前关于钢弹簧隔振器的研究可总结为：获取并归纳力学参数变化规律[1-6]、优化与改进力学模型[7-12]、钢弹簧对浮置板轨道动力响应的影响[13-16]。钢弹簧隔振器动反力特征是造成钢弹簧性能劣化的根本原因，研究钢弹簧动反力特征对指导钢弹簧隔振器参数设计与疲劳分析具有重要意义，但目前关于钢弹簧隔振器动反力特征的研究尚不够成熟。

李忠继等[17]利用有限元方法建立列车、浮置板轨道模型，并通过模态叠加法、轮轨相互作用模型建立列车-连续型浮置板轨道系统动力学模型，计算浮置板中部钢弹簧隔振器的动反力，其研究以某一确定的轨道不平顺样本作为轮轨激扰输入，未考虑轨道不平顺随机性引起的钢弹簧隔振器垂向动反力统计学特征。李俊岭等[18]将钢轨模拟为离散支承欧拉梁、浮置板模拟为离散支承有限长自由梁，建立列车-浮置板轨道(train-floating slab track，T-FST)耦合垂向动力学模型，计算分析钢弹簧隔振器垂向动反力的动力特性，其研究同样未考虑轨道不平顺随机性引起的钢弹簧隔振器垂向动反力统计学特征，也未研究参数变化对钢弹簧隔振器反力频率成分的影响规律；同时其采用模态叠加法建立浮置板振动方程，该方法在选取模态时难以全面考虑轨道结构局部高频振动模态，从而存在着无法准确计算钢轨局部振动与轮轨之间相对位移的缺点。由于车-轨耦合系统振动响应是一个随机过程[19]，赵岩等[20-22]的研究表明，对少量轨道不平顺样本计算得到的动力响应时程结果进行统计分析是缺乏可靠性的，无法完全反应结构随机振动响应的全部特征。Lu等[23]直接指出轨道不平顺引起的列车-结构耦合振动应该采用随机振动的方法进行研究。虚拟激励法(pseudo excitation method,PEM)是研究随机振动的一种手段，与传统的Monte-Carlo等方法相比具有更高计算效率与精度[24-28]。

因此，本文通过虚拟激励法将轨道高低不平顺转化为一系列简谐不平顺的叠加，将非平稳随机振动问题转化为确定性时间历程问题，建立了车辆-浮置板轨道耦合系统竖向随机振动模型。基于该随机振动模型，揭示了钢弹簧隔振器动反力随机特征，研究了轨道不平顺、车速对钢弹簧隔振器动反力随机特征的影响规律，为进一步研究环境振动、钢弹簧疲劳荷载谱以及钢弹簧参数设计提供理论研究基础。

1 列车-浮置板轨道动力学模型

1.1 列车模型

由于钢弹簧隔振器动反力主要由列车垂向作用引起，故本文仅考虑垂向向振动自由度，每节车体共有10个自由度。列车的运动方程为

(1)

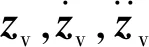
1.2 浮置板轨道模型

模态叠加法难以全面考虑轨道结构局部高频振动模态，导致无法准确计算钢轨局部振动与轮轨之间相对位移。而通过建立有限元模型，采用直接刚度法，不需要人为设定分析截至频率，计算精度较高。因此为了更加准确计算钢弹簧垂向动反力，本文采用有限元直接刚度法建立浮置板轨道动力方程。

(2)

式中，Mb，Kb，Cb分别为浮置板轨道子系统的质量矩阵、刚度矩阵、阻尼矩阵，可以在ANSYS软件中直接获得。其中阻尼矩阵Cb包括轨道板本身的材料阻尼、钢弹簧及轨下弹簧-阻尼器单元阻尼，采用Rayleigh阻尼来模拟轨道结构的阻尼特性，可表示为

(3)

式中：α，β为Rayleigh阻尼系数，根据浮置板轨道的前两阶竖向自振频率ω1，ω2计算，阻尼比取2%[29]；Ne为具有单元阻尼的单元类型数；Ci为第i个弹簧-阻尼器单元的阻尼。建立的列车-浮置板轨道耦合振动模型如图1所示。

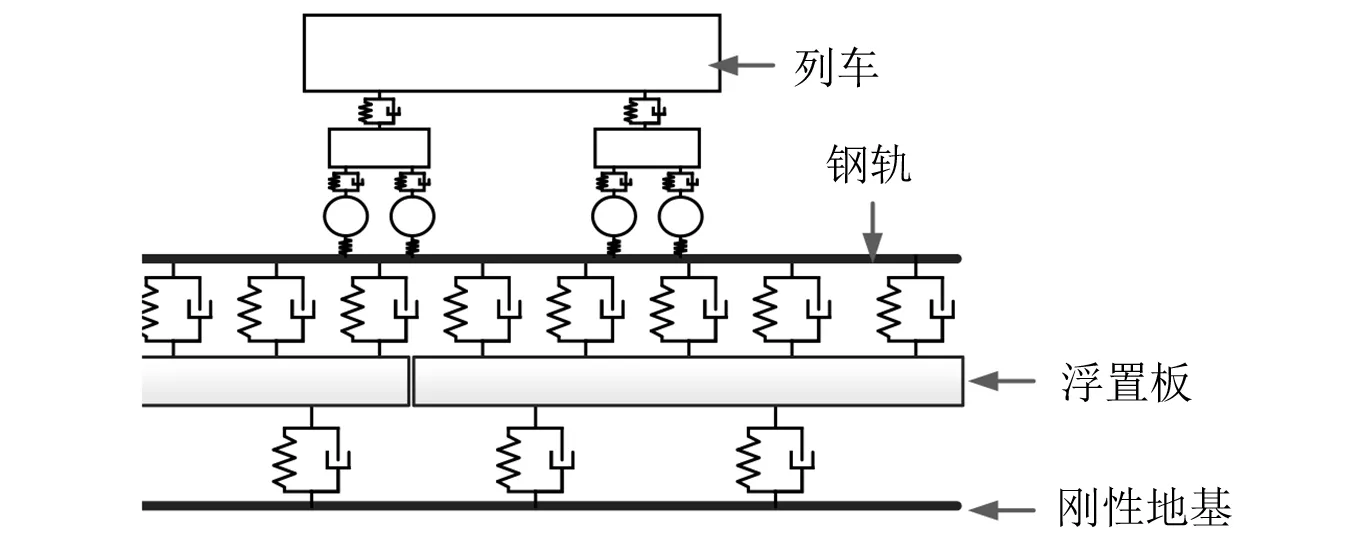
图1 列车-浮置板轨道耦合振动模型Fig.1 Dynamic model of T-FST coupled system

1.3 轨道不平顺模型

由于目前尚缺少与“地铁无砟轨道不平顺谱”直接相关的资料，目前已有研究中多用美国六级谱来模拟城市地铁的轨道不平顺[30-34]，为分析钢弹簧隔振器动反力受不同轨道不平顺条件的影响，本文参考已有文献并采用下列几种常用的轨道不平顺谱进行研究，且只考虑轨道高低不平顺：①美国六级谱；②美国五级谱；③美国四级谱。各类轨道不平顺谱的具体表达式可参考文献[35]。

1.4 轮轨接触模型

列车子系统和浮置板轨道子系统之间通过轮轨接触关系耦合成一个整体。目前处理轮轨垂向接触关系主要基于两种模型：①忽略轮轨相对变形的密贴模型；②考虑轮轨相对变形的Hertz接触模型。虽然密贴模型理论上较为简单，但其忽略了轮轨之间相对变形，从而难以真实反映轮轨之间的动态相互作用。因此本文采用考虑轮轨相对变形的Hertz接触模型模拟轮轨接触关系[36]，轮轨接触刚度按照式(4)求解

(4)

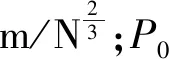
2 基于虚拟激励法的钢弹簧隔振器动反力计算

2.1 列车-浮置板轨道耦合时变系统随机振动分析

通过轮轨接触关系将车辆子系统和轨道子系统组成整体耦合时变系统，可建立列车-浮置板轨道耦合时变系统动力方程，如式(5)所示

(5)

列车-浮置板轨道耦合系统所受的外荷载F由以下两个成分组成：列车自质量确定性激励F1(t)和轨道不平顺随机激励F2(t)，即

F=F1(t)+F2(t)

(6)

根据随机振动理论，轨道不平顺激励F2(t)可写为

F2(t)=Γ(t)G(t)x(t)

(7)

G(t)=diag[g(t-t1)]…g(t-t1)…
g(t-tNw)]

(8)

x(t)=[x(t-t1)…x(t-t1)…x(t-tNw)]T

(9)

式中：Γ(t)为作用力指示向量；G(t)为慢变均匀调制函数矩阵；x(t)为轨道不平顺多点异相位平稳随机激励向量；Nw为列车轮对总数。

本文假设轨道不平顺是零均值的平稳随机过程，因此列车-浮置板轨道耦合系统随机响应的均值是由列车自质量确定性激励F1(t)引起的。对轨道不平顺随机激励F2(t)构造虚拟激励

(10)

则由此引起的列车-浮置板轨道耦合系统的虚拟响应为

(11)

Sxx(ω)=Sv(Ω)/v,ω=Ωv=2πv/λ

(12)

式中：H(t-τ)为脉冲响应函数；Sxx(ω)为轨道不平顺x(t)的功率谱密度函数；Sv(Ω)为空间域功率谱密度函数，Ω为空间圆频率，rad/m；ω为时间圆频率，rad/s；λ为轨道不平顺的波长，m。

随机响应的自谱密度矩阵Szz(ω,t)如式所示，求出随机响应的自谱密度矩阵Szz(ω,t)后，通过频域内积分并开方就可得到系统随机响应的标准差。

HT(t-τ2)dτ1dτ2=Szz(ω,t)

(13)

由于车辆匀速运行，假定x=vt为第1个车轮在t时刻位置离轨道起点的距离，则车轮在时间域受到的轨道不平顺激励为

zx(t)=g(t)x(t)

(14)

式中，g(t)为慢变均匀调制函数，取

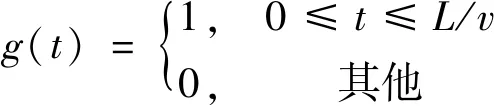
(15)

同一条轨道上的任意两车轮受到相同的轮轨间随机激励，但是会由于车轮间距存在相位差，轨道不平顺引起的第i节车辆第l个轮对垂向位移zxil为

zxil=zx(t-Δtil)

(16)

式中，Δtil为第i节车辆第l个轮对与第1个轮对作用时间上相差的常因子。则第i节车辆第l个轮对受到的虚拟轨道不平顺为

(17)

因此，该轮对所受虚拟轮轨力为：

(18)

2.2 钢弹簧隔振器动反力

列车行驶过程中，钢弹簧隔振器垂向动反力F可写成

F=kΔx+cΔv

(19)

式中：k，c分别为钢弹簧隔振器竖向刚度、竖向阻尼；Δx，Δv为钢弹簧隔振器顶部、底部位移之差与速度之差。

一般认为，受浮置板自质量静压作用，钢弹簧隔振器自身固有频率与浮置板自振频率(6～16 Hz)相当，李俊岭等的研究表明：地铁列车行驶过程中，由车辆自身结构特性引起的钢弹簧隔振器动反力主频远小于钢弹簧自身固有频率；王建伟等开展现场试验，研究了加载频率为1～10 Hz的钢弹簧隔振器动态特性参数变化，其研究结果表明：钢弹簧隔振器动态参数仅在其共振频率附近相比静态参数增大10%，对于其它加载频率则增大3%～5%左右。因此对于一般情况下的地铁浮置板轨道，列车行驶不会引起钢弹簧隔振器共振、钢弹簧隔振器刚度与阻尼不会产生较大的变化，故本文简化考虑k，c分别为静态下钢弹簧隔振器竖向刚度、竖向阻尼。

工程设计中，钢弹簧隔振器垂向动反力的最大值通常是重点关注对象，本文基于3倍标准差法则确定具有99.7%保证率的钢弹簧隔振器垂向动反力随机特征上下限值。同时，根据2.1节列车-浮置板轨道耦合时变系统随机分析方法，开发了相应的计算程序，具体计算流程如图 2所示。

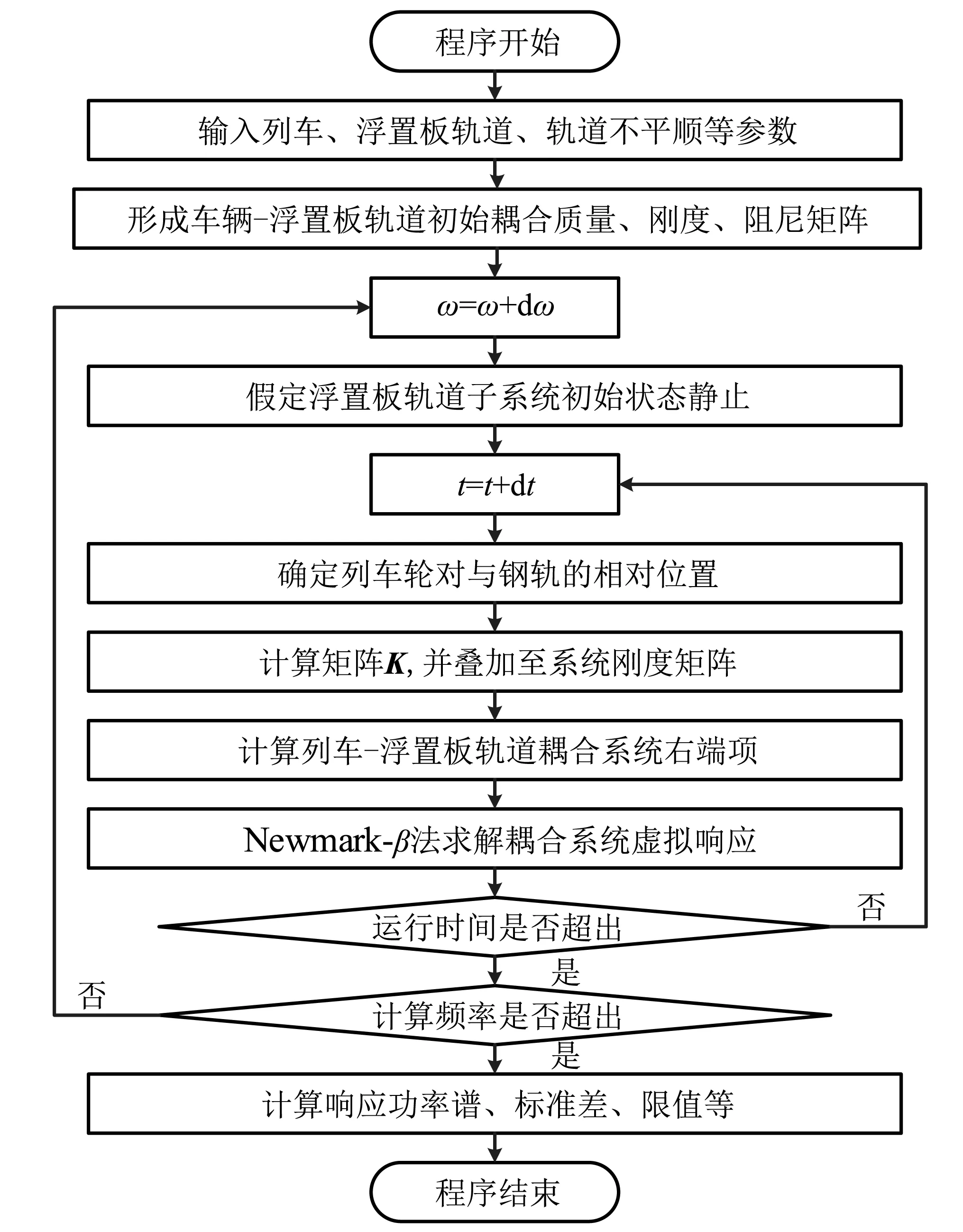
图2 列车-浮置板轨道耦合系统随机振动分析流程图Fig.2 Flowchart for the random vibration analysis of T-FST model

3 模型验证

本文采用文献[37]中的车辆及钢弹簧浮置板轨道动力学参数，并基于本文的列车-浮置板轨道耦合时变系统随机分析方法及自编程序，计算了浮置板在不考虑剪力铰连接作用时，6车编组的地铁车辆以60 km/h速度在轨道不平顺为美国六级谱的轨道上运行的系统竖向振动，并将本文计算结果与Ma等研究的结果进行对比以验证本文模型及程序的正确性。

图3和表1分别给出了钢轨和轨道板在行车方向距离模型始端54 m处的浮置板与钢轨竖向位移时程曲线和最大值结果，从图表结果可以看出本文方法计算得到的钢轨和轨道板竖向位移和Ma等研究中的结果基本一致，说明本文方法能够较好地反映列车-浮置板耦合振动特性。

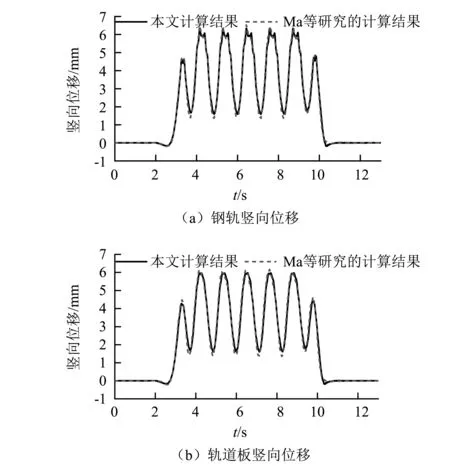
图3 浮置板轨道位移时程对比Fig.3 Comparison of time-history results of FST displacement

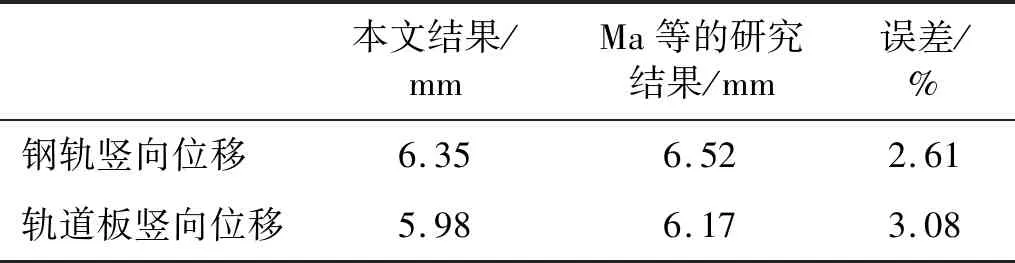
表1 钢轨和轨道板竖向位移最大值对比Tab.1 Comparison of maximum vertical displacement results of rail and slab

4 计算结果与分析

4.1 钢弹簧浮置板轨道有限元模型

以实际工程中采用的一种钢弹簧浮置板轨道作为研究对象，开展钢弹簧隔振器垂向动反力研究。其中，预制轨道板尺寸(长×宽×厚)为4.8 mm×2.7 mm×0.34 mm，混凝土强度等级为C50，每块轨道板以1.2 m为间隔设置4对钢弹簧隔振器，以0.6 m为间隔设置8对扣件，相邻轨道板间设置4块剪力铰相连。

本文采用ANSYS软件建立浮置板轨道有限元模型，如图4所示。为了消除边界条件对数值计算结果的影响，模型中建立了25块4.8 m长的轨道板(图4展示了第1～第3块浮置板)，首尾各有24 m的钢轨延长段。钢轨采用beam188单元模拟，为了考虑轨道结构的高频振动，单元长度为0.1 m。轨道板采用solid45单元模拟。根据剪力铰在实际浮置板轨道结构中起到的抗弯与抗剪作用，在相邻轨道板接缝处采用抗弯和抗剪弹簧模拟剪力铰的作用，参数分别为设为5×108N·m/rad，5×108N/m。采用combin14单元模拟轨下扣件以及钢弹簧隔振器的弹性支撑作用，底部为全约束，扣件与钢弹簧隔振器的具体参数如表2所示。

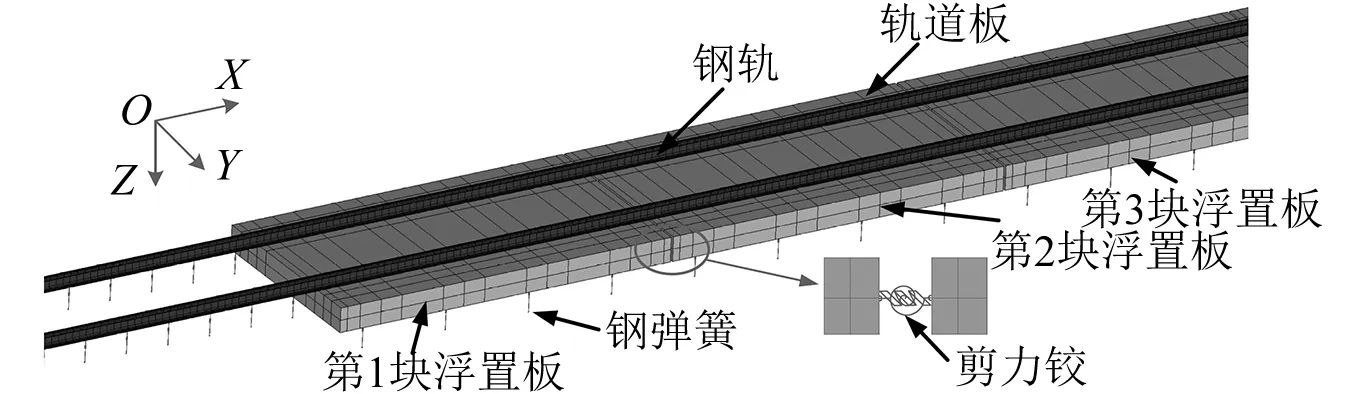
图4 浮置板轨道有限元模型Fig.4 Finite element model of FST

表2 扣件与钢弹簧参数Tab.2 Parameters of fastner and steel-spring

4.2 钢弹簧隔振器动反力随机特性分析

基于列车-浮置板轨道耦合系统随机动力学模型，取6车编组地铁B型车(参数见表3[38])以80 km/h速度单线通过浮置板轨道的计算结果，对钢弹簧隔振器动反力随机特征进行研究。轨道不平顺为美国六级谱，波长范围为1～100 m。以图4所示有限元模型为例，取第13块浮置板(位于整个浮置板轨道结构跨中)一侧由板端到板末的第2个钢弹簧隔振器为研究对象，如图5中F所示。

图5 钢弹簧隔振器位置示意图Fig.5 Schematic diagram of steel spring isolator position

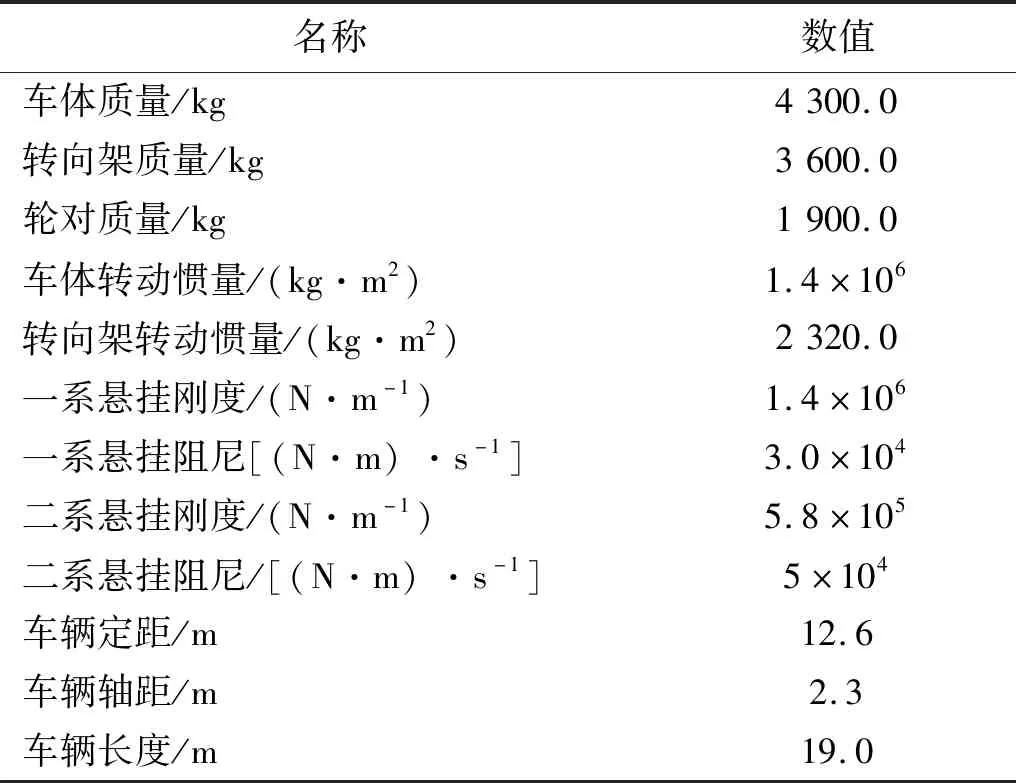
表3 地铁B型车计算参数Tab.3 Parameters of B type metro train

图6给出了该钢弹簧隔振器动反力的随机特征，从图中可以得到：

(1)钢弹簧隔振器动反力受车辆轴质量确定性激励控制，其中随机激励引起的钢弹簧动反力标准差最大值约为确定性激励引起的钢弹簧动反力均值最大值的1.7%。

(2)根据三倍标准差法则计算的钢弹簧隔振器动反力上限值和下限值的最大值分别为29.85 kN与27.22 kN，上限值和下限值最大值相差2.63 kN；相对于钢弹簧隔振器动反力均值最大值的变化在4.6%～-4.8%。

通过对图6(a)钢弹簧隔振器动反力均值做快速Fourier变换，可以得到动反力均值的功率谱密度(power spectral density,PSD)曲线，如图7(a)所示；图7(b)给出了基于虚拟激励法得到的随机激励下钢弹簧隔振器动反力的时变PSD 云图。从图7(a)可知，当车速为80 km/h 时，主频f1=0.077 Hz，(1/f1)与列车通过浮置板轨道的加载时间t接近；同时，与车辆长度相关的加载频率fv≈f2(fv=v/lv=1.17 Hz，v和lv分别为车速和车辆长度)，说明车辆长度的周期性激励对钢弹簧反力影响较大。从图7(b)可知，随机荷载激励下钢弹簧反力的主频大致分布在两个连续的频段0.22～1.78 Hz和6.67～13.32 Hz内，分别与车辆长度引起的周期性加载频率(fv=1.17 Hz)，车辆轴距引起的周期性加载频率(ft=v/lt=9.66 Hz，lt为车辆轴距)密切相关。

图6 钢弹簧隔振器动反力随机特征Fig.6 Random characteristics of vertical DRF of steel spring isolators

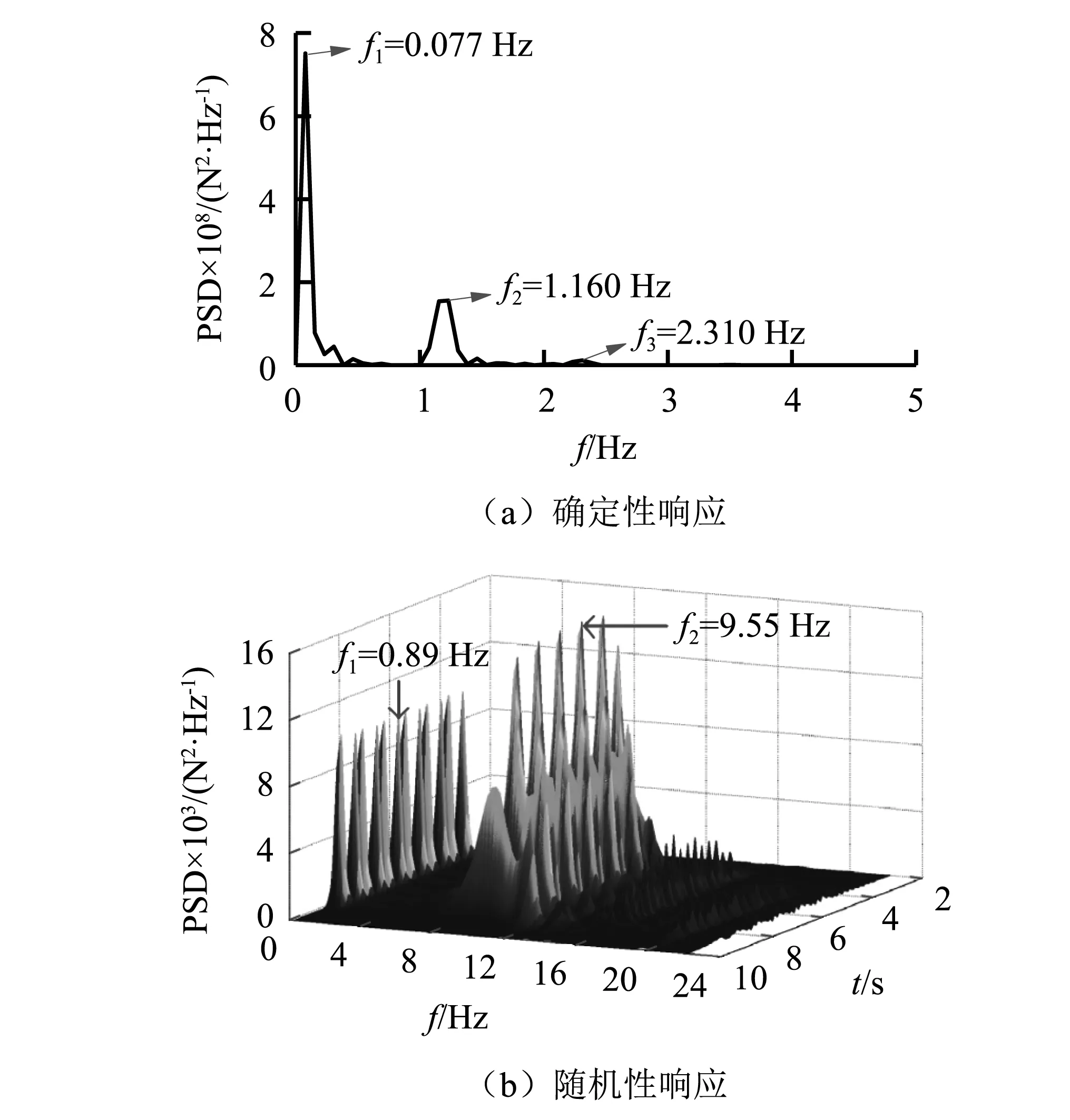
图7 钢弹簧隔振器动反力功率谱Fig.7 Spectrum of vertical DRF of steel spring isolators

4.3 轨道不平顺对钢弹簧隔振器动反力的影响

由4.2节分析可知，轨道不平顺对钢弹簧隔振器动反力影响不可忽略，本节将通过对比车速为80 km/h条件下不同轨道不平顺引起钢弹簧隔振器动反力随机响应的特征，研究轨道不平顺对钢弹簧隔振器动反力均值(μ)、标准差(σ)、上限值(μ+3σ)的影响规律。

图8给出了不同轨道不平顺下钢弹簧隔振器动反力的随机特征，表4给出了不同轨道不平顺下统计参数最大值以及根据上限值与静力情况下钢弹簧隔振器反力最大值计算的放大系数。不同轨道不平顺下钢弹簧反力的标准差时程曲线波形相似，幅值大小不同，说明：尽管轨道不平顺等级不同，但是列车经过时，对钢弹簧反力造成的离散性随时间的变化规律是一致的；美国四级谱(FAR4)引起的钢弹簧反力标准差最大，美国六级谱(FAR6)引起的钢弹簧反力标准差最小，二者标准差最大值相差1.42 kN，上限值最大值相差3.94 kN，表明尽管钢弹簧隔振器动反力受轨道不平顺激励影响较小，但随着轨道不平顺的劣化，钢弹簧隔振器动反力仍会进一步增大。同时，轨道不平顺的劣化使得动力放大系数迅速增大，从而加剧环境振动。

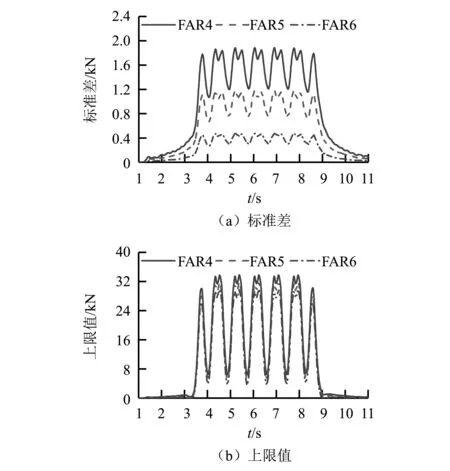
图8 不同轨道不平顺下钢弹簧隔振器动反力随机特征Fig.8 Random characteristics of vertical DRF of steel spring isolators under different track irregularity level

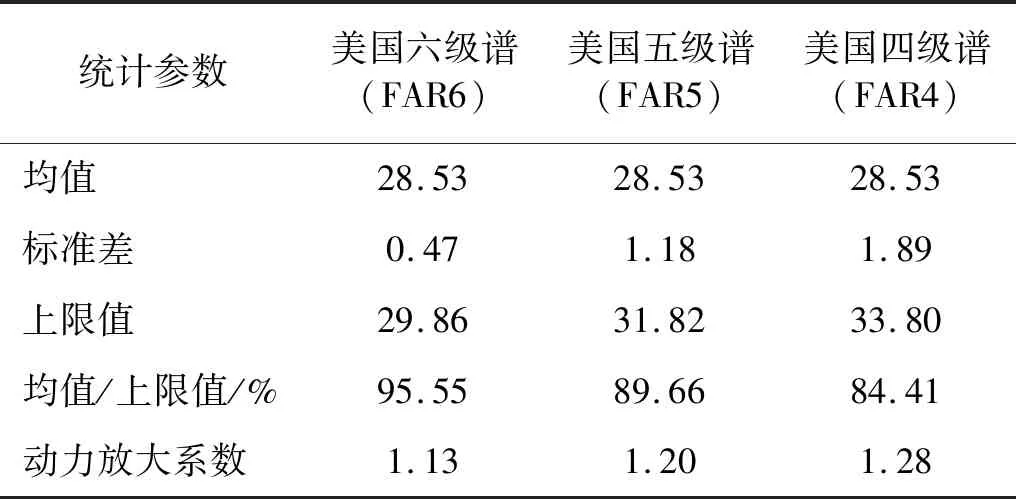
表4 不同轨道不平顺下统计参数最大值Tab.4 Statistical parameter maximum values of vertical DRF under different track irregularity level

图9给出了3种轨道不平顺下钢弹簧隔振器动反力功率谱。从图中可以得出以下结论：不同的轨道不平顺对钢弹簧隔振器动反力功率谱的主频分布没有影响，钢弹簧反力功率谱的主频主要和车辆长度和车辆轴距引起的周期性加载频率有关(分别为9.55 Hz与0.89 Hz)。说明同一行车条件下，不同轨道不平顺对二者有影响的波长范围相似，但轨道不平顺等级越差，各频点处的功率谱幅值越大。

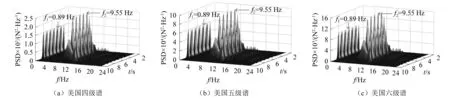
图9 不同轨道不平顺条件下钢弹簧隔振器动反力功率谱Fig.9 Spectrum of vertical DRF of steel spring isolators under different track irregularity level

4.4 车速对钢弹簧隔振器动反力的影响

近年来，国内城市轨道交通逐步开通了120 km/h的地铁线路，未来可能会进一步提速。列车运行速度对车辆-浮置板轨道耦合系统的动力响应影响显著，为研究钢弹簧隔振器动反力随机特征随车速的变化规律，本文选取轨道不平顺为美国六级谱，对6种车速情况进行分析，分别为：40 km/h，60 km/h，80 km/h，100 km/h，120 km/h，140 km/h。

图10给出了钢弹簧隔振器动反力统计参数最大值随车速变化规律，表5给出了统计参数的最大值以及根据上限值与静力情况下钢弹簧隔振器反力最大值计算的放大系数，从图表中可以看出：当车速从40 km/h增大到140 km/h时，钢弹簧反力均值最大值从28.29 kN增大到28.93 kN，标准差最大值从0.17 kN增大到0.71 kN，上限值最大值从28.76增大到31.05 kN，均值占上限值的比值由98.37%减小为93.17%，说明列车轴质量引起的钢弹簧隔振器动反力均值受车速影响较小，轨道不平顺引起的钢弹簧隔振器动反力标准差受车速影响较大，车速越大，钢弹簧隔振器动反力的离散性越大，引起的环境振动越剧烈。车速越大，钢弹簧隔振器动反力的动力放大系数也越大。由图10(c)计算值知，钢弹簧隔振器动反力上限值与速度近似呈线性关系，本文拟合了上限值与速度计算的公式如下，拟合曲线如图10(c)所示

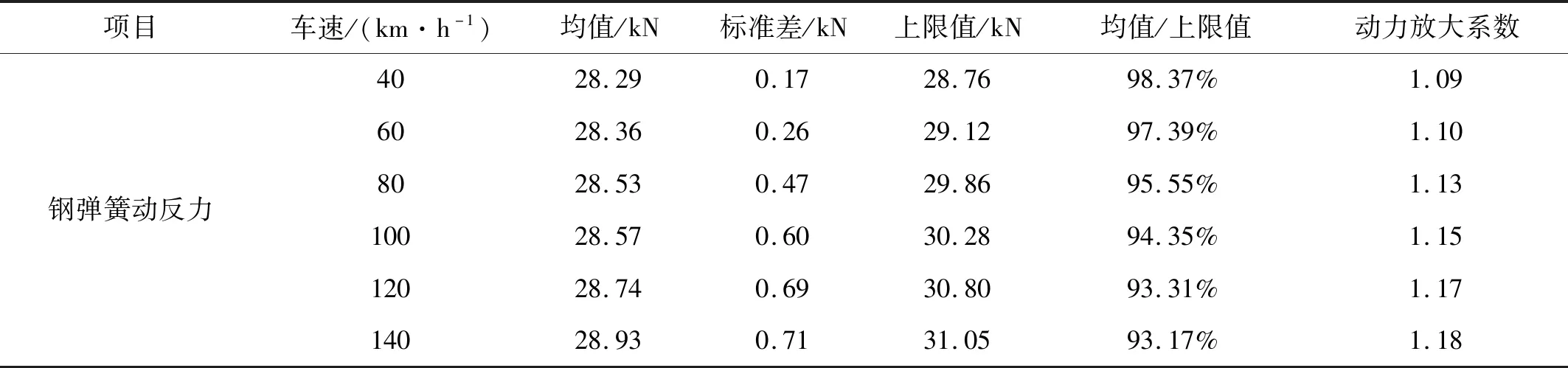
表5 不同车速下钢弹簧隔振器动反力统计参数最大值Tab.5 Statistical parameter maximum values of vertical DRF under different train speed

图10 钢弹簧隔振器动反力统计参数最大值随车速变化规律Fig.10 Statistical parameter maximum values of vertical DRF varying with train speed

Fu=0.024 16v+27.8

(20)

式中：Fu为钢弹簧隔振器动反力上限值，kN；v为车速，km/h。拟合公式的残差平方和为0.06，线性拟合度评价指标R平方为0.98。

图11(a)～图11(f)分别给出40～140 km/h车速下，轨道不平顺随机激励引起的钢弹簧隔振器动反力功率谱，从图中结果可以得出以下结论：

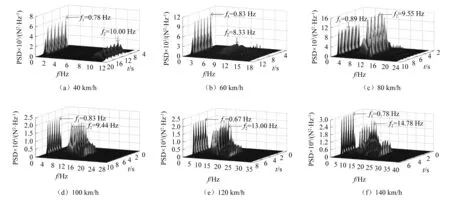
图11 不同车速下钢弹簧隔振器动反力功率谱Fig.11 Spectrum of vertical DRF of steel spring isolators under different trainspeed

(1)当车速小于60 km/h时，钢弹簧隔振器动反力随机分量主要集中在与车辆长度周期性加载频率相近的低频段，随着车速的增大，中短波分量引起的振动频率被激发，该频率与车辆轴距周期性加载频率相近，此时轨道不平顺引起的钢弹簧反力随机分量主要集中在两个连续的频段。

(2)当车速为80km/h时，车辆轴距引起的周期性加载频率ft=v/lt=9.66 Hz，而本文所研究浮置板轨道的一阶自振频率约为10.51 Hz，二者相近，易发生共振，因此在此车速下钢弹簧反力功率谱在频率f2的值大于f1，其余车速下f1值均大于f2。

5 结 论

本文基于有限元法与虚拟激励法，建立了列车-浮置板轨道耦合系统竖向随机振动模型，以6车编组的地铁B型车通过钢弹簧浮置板轨道为算例，研究了车辆-浮置板轨道耦合系统的竖向随机振动特征，分析了轨道不平顺和车速对钢弹簧隔振器垂向动反力的影响规律，得出了如下结论：

(1)本文建立的列车-浮置板轨道耦合系统竖向随机振动模型，可以准确的求解得到车辆、浮置板轨道振动响应的均值(μ)、标准差(σ)和限值(μ±3σ)等统计参数。在轨道不平顺随机激励下，任意时刻的振动响应并非确定值，而是介于下限值(μ-3σ)和上限值(μ+3σ)之间。钢弹簧隔振器动反力主要受列车轴质量确定性激励影响。

(2)钢弹簧隔振器动反力受轨道不平顺激励影响较小，但随着轨道不平顺的劣化，动反力会进一步增大，动力放大系数也随之迅速增大，加剧环境振动；不同的轨道不平顺对钢弹簧隔振器动反力功率谱的主频分布影响不显著，说明同一行车条件下，不同轨道不平顺对二者有影响的波长范围相似。

(3)钢弹簧隔振器动反力统计参数随着车速的增大而增大，钢弹簧隔振器动反力上限值与速度近似呈线性关系；车速越大，动力放大系数增大，轨道不平顺引起的离散性越大，钢弹簧隔振器动反力随机分量主要集中分布在两个连续的频段内，分别与车辆长度周期性加载频率和车辆轴距周期性加载频率密切相关，车速增大，中短波分量引起的振动频率参振越大。