考虑环境因素影响的海洋平台结构损伤检测研究

吴文开，徐明强，王树青，蒋玉峰，王国兴

(1.中国海洋大学 工程学院，山东 青岛 266100；2.山东交通学院 船舶与港口工程学院，山东 威海 264200)

海洋平台体积庞大、结构复杂，且长期服役于恶劣的海洋环境下，结构损伤逐渐累积。为保证结构作业的安全性与耐久性，对海洋平台进行健康监测是必不可少的[1]。由于具有全局、自动化检测的能力，基于结构振动特性的损伤检测技术在结构健康监测领域得到了广泛重视，学者们发展出了一系列的损伤检测方法[2]。其基本思想是:损伤会改变结构的物理属性(例如刚度)，进而影响结构的动力特性，反过来，利用结构的动力特性构建损伤灵敏度指标，即可实现损伤判定[3]。然而，常用的损伤指标，如结构频率，极易受到海洋环境因素(如温度、潮汐、海生物附着等)变化的影响，以致在实际应用中难以准确反映出结构损伤[4]。为了将损伤检测方法更好地推广到工程实践，发展能够消除环境因素影响的损伤检测技术至关重要。

温度是影响结构刚度变化的一种典型环境要素[5]。Askegaard等[6]在对一座三跨钢筋混凝土人行桥为期3年的监测中发现，季节性的温度变化对桥梁频率的改变达到了10%。Doebling等[7]对美国阿拉莫斯峡谷大桥进行的模态测试则表明，气温日变化引起大桥1阶频率的改变接近5%。然而，Farrar等[8]对I-40桥进行破坏性试验时发现，将桥梁一侧的工字梁沿横截面切割1/2，其1阶频率的改变仅为8%。不难看出，环境因素的变化对结构动力响应的影响较为明显，在一定程度上会掩盖结构真实损伤，从而导致损伤误判和损伤漏判的发生。

已有的考虑环境因素影响的损伤检测方法主要分为两大类：一类是建立环境因素与结构动力响应之间的相关性模型，Peeters等[9]建立了ARX模型，通过测量温度的变化预测结构频率，当预测频率与识别频率不吻合时认为结构发生了损伤，然而此类方法要求环境因素是可测的，但对海洋结构而言，由于其服役环境相当恶劣，通常不具备可测量条件；第二类方法考虑了环境因素不可测量或难以测量的情况，此类方法将结构动力响应分解成结构损伤和环境因素影响两个部分，仅需要响应信息，是近年来的研究热点。应用较为广泛的有主成分分析(principal component analysis，PCA)和协整分析(cointegration analysis，CA)等。

Yan等[10]考虑了线性或弱非线性环境因素变化的影响，首次将通过PCA降维处理后得到的残差作为损伤指标，以一个三跨桥的有限元模型和一个木桥的物理模型试验对方法的有效性进行了验证。随后，Yan等[11]融合了两种新型聚类策略，将PCA方法进一步推广到处理环境因素的非线性影响。吴森等[12]先利用PCA消除一钢结构平台动态响应中的温度影响，继而以小波包系数节点能量谱计算结构损伤敏感特征来识别结构损伤。常鹏等[13]采用结构响应的小波包能量谱作为特征参数的输入，以主成分残差作为损伤指标，通过一个藏式古建筑两年的实测数据验证了该方法可以剔除温度变化的影响。Wang等[14]采用PCA方法消除振型数据中的环境影响，进而构造反映结构真实状态的残差应变能，通过多变量假设检验进行损伤判定，对某一海上风机现场监测数据的分析表明，该方法可有效避免误判问题。

Cross等[15]首先提出采用响应数据的协整残差作为损伤判定指标，并以一个温度变化条件下的层合板损伤试验验证了该方法的有效性。由于实际信号可能在不同的时间尺度下具有不同的共同趋势，Worden等[16]先对信号进行多分辨分析，进而求解各时间尺度下分解信号的协整残差，在一定程度上提高了协整方法的损伤检测灵敏度。梁亚斌等[17]采用EG(engle-granger)两步协整求解结构前2阶频率的协整残差，通过钢筋混凝土梁和钢桁架桥的数值模拟表明该方法可有效消除温度影响且具有一定的噪声鲁棒性。刁延松等[18]以测点响应的AR(autoregressive model)模型系数作为协整变量，通过一个海洋平台模型的实验证明了所提方法可以有效消除温度变化的影响。Huang等[19]发展了一种基于卡尔曼滤波和协整的损伤识别方法，先通过协整系数构建卡尔曼滤波的状态向量，而后利用递归过程在线估计结构状态的变化，将该方法应用于天津永和大桥，成功地识别出了两处结构损伤。

PCA和CA均为多元统计分析的重要内容，两者颇有类似之处。然而，在健康监测领域尚未对两种方法进行过比较研究。本文以一个海洋平台模型为例，考虑空气、海水和海底泥土温度变化的联合影响，以结构的模态频率作为样本数据，以X-bar控制图作为损伤判别标准，分析比较两种方法在损伤识别效果以及噪声鲁棒性方面的性能差异，为海洋平台损伤检测方法的选取提供参考借鉴。

1 主成分分析(PCA)

1.1 基本原理

PCA又称“Karhunen-Loeve变换”、“本征正交分解”，是一种多元统计分析方法。PCA通过求解样本数据协方差矩阵的特征值问题，以前几阶特征向量构造的主成分代替样本数据，达到了简化问题和减少计算量的目的。

取结构n阶模态频率的N个观测值，对频率作中心化处理，组成N×n阶测量频率矩阵X，其协方差矩阵可表示为

(1)

则主成分分析的实质是求解以下特征值问题

CΦ=ΛΦ

(2)

式中：Λ=diag(λ1,λ2,…,λn)为由n个特征值组成的对角矩阵，且λ1≥λ2≥…≥λn;Φ=[φ1,φ2,…,φn]为与特征值对应的特征向量所组成的特征向量矩阵。

设定能量阈值ε，使得对于前k(k≤n)个特征值，满足

(3)

则前k个特征向量为主成分向量，可构成投影矩阵

T=[φ1,φ2,…,φk]

(4)

进而得到原频率矩阵基于低维空间的估计

(5)

定义残差矩阵

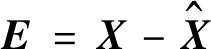
(6)

则第t个观测值对应的残差向量为et=[et1,et2,…,etn]，对其求Euclid范数，可得到描述观测值与估计值之间偏离程度的主成分残差

(7)

1.2 X-bar控制图

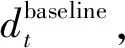
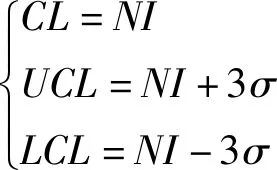
(8)

由于主成分分析已消除了环境因素的影响，因此正态分布假设下基准数据对应的主成分残差位于区间[NI-3σ,NI+3σ]内的概率为99.74%。

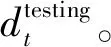
(9)

此外，测试数据和基准数据的残差均值比

(10)

也可以作为损伤判别标准，该比值趋于1，则结构正常，当残差均值比较大时可以认为结构发生了损伤。

考虑到样本数目的有限性，用于定量描述结构损伤的异常值比例不宜设置过小，本文以异常值比例超过10%，残差均值比超过1.5作为损伤判别标准。

2 协整分析

2.1 协整理论概述

从时间序列分析的角度看，协整就是将一组具有长期共同趋势的时间序列，通过线性组合的方式规整为一个时间序列，这个新的序列在反映了原始序列特征的同时，已经消除了共同趋势。对于结构频率时间序列(即一系列采集的结构频率数据)而言，这种长期的共同趋势通常是由环境因素变化引起的。

为了更好地理解协整的概念，首先需要定义单整过程。如果一个非平稳随机时间序列{yt,t=1,2,…,N}经过d次差分后为平稳过程，则{yt}为d阶单整过程，记为yt～I(d)。现假设一组d阶单整的非平稳序列yt=[y1t,y2t,…,ynt]T，如果其线性组合

ζt=β1y1t+β2y2t+…+βnynt

(11)

为d-1阶单整序列，即为I(d-1)过程，则yt中的各序列存在协整关系。其中β=[β1,β2,…,βn]T称为协整向量。

2.2 平稳性检验

由2.1节可知，协整与时间序列的单整阶数，即平稳性密切相关，因此在协整分析前，需要对时间序列进行平稳性判断，通常用增广单位根(augmented Dickey-Fuller，ADF)进行检验[20]。构造时间序列{yt}的p阶自回归模型AR(p)的误差修正形式

(12)

式中：Δ为差分算子；ρ和γj为模型系数；εt为高斯白噪声序列。

若{yt}是非平稳过程，则模型至少有一单位根，对应ρ=0。故可作以下假设检验

H0∶ρ=0,H1∶ρ<0

(13)

检验统计量为

(14)

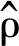
若拒绝H0，则{yt}是平稳序列，即yt～I(0)。若接受H0，则{yt}是非平稳序列，需构造原序列差分{Δyt}的自回归模型，并根据式(13)进行假设检验。以此类推，如果对于{Δkyi(t)}的自回归模型拒绝H0，则yt～I(k)。由于实际观测序列通常不是发散的，因此多为I(1)或I(2)过程。

2.3 Johansen方法

对于一个n维多元时间序列yt=[y1t,y2t,…,ynt]T，若其各序列同为1阶单整，即∀yit～I(1)，i=1,2,…,n，t=1,2,…，N，则可通过Johansen方法估计协整向量β，其实质是对yt的向量自回归模型(vector auto regression,VAR)的参数作极大似然估计[21]。

首先构造多元时间序列yt的p阶向量自回归模型VAR(p)

(15)

式中：Πi和Φ为系数矩阵;εt为多元高斯白噪声过程，有εt～N(0,Ω);dt为确定性趋势。通过适当的变换，可以得到模型的误差修正形式

(16)

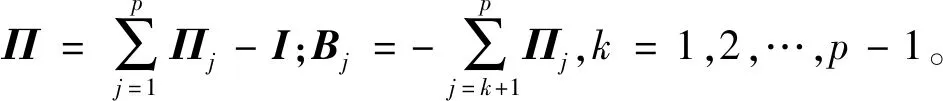
Johansen方法认为，如果n个时间序列之间存在协整关系，则系数矩阵Π必不满秩，设rank(Π)=m，则原序列yt有m个协整向量，且存在n×m的满秩矩阵α和β，满足

Π=αβT

(17)

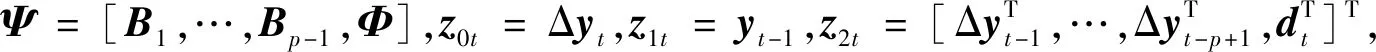
z0t=αβTz1t+Ψz2t+εt

(18)

忽略常数系数(2π)-nN/2，则似然函数为

(19)

从而得到Ψ的极大似然估计为

(20)

r0t=αβTr1t+εt

(21)

(22)

记m个特征值λ1≥λ2≥…≥λm及对应的特征向量为φ1,φ2,…,φm，通常取最大的特征值对应的特征向量作为协整向量。

2.4 模型定阶

在进行Johansen协整检验之前，需要先确定模型的滞后阶数p，在正态分布假设下，通常可采用AIC，BIC和HQ信息准则。文献[22]认为，由BIC准则确定的模型得到的极大似然估计的效果更好，因此本文采用BIC准则进行定阶，其表达式为

(23)

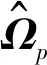
2.5 协整秩检验

通过求解式(22)，我们可以找到协整向量，但是我们并不能保证各变量确实存在协整关系，为此，Johansen提出了似然比统计量。

(24)

(25)

且观察式(19)发现似然函数有上界

(26)

考虑假设检验

H0∶r=m,H1∶r>m

(27)

式中，r为系数矩阵Π的秩，即为协整的秩。

引入似然函数比Q并结合式(22)、式(24)～式(26)，有

(28)

构造负对数似然比统计量LR

(29)

其渐近分布为

LR⟹ tr{f(Wr)[f(Wr)]-1f(Wr)}

(30)

式中，tr{·}为矩阵的迹，且有

(31)

式中，Wr为n-r维维纳过程。LR统计量的临界值与协整秩r有关，可以通过数值模拟得到。检验的流程按照假设r=0,1,…,n-1依次进行。当LRm大于临界值时，拒绝H0，表明协整关系的个数大于m，检验继续，直至不能拒绝H0为止。若此时统计量为LRm*，则说明原时间序列存在m*个协整关系。

2.6 损伤判定

根据式(22)求得的结果，取最大的特征值对应的特征向量作为协整向量，即β=φ1，则第t个样本对应的协整残差为

(32)

为方便与PCA方法作对比，对协整残差作中心化处理

ξt=|ζt-μξ|

(33)

式中，μξ为基准数据协整残差的均值。

对比式(2)和式(22)可以看出：主成分分析的核心算法是求解样本数据协方差矩阵的特征值问题，再取原始数据与估计数据的残差作损伤判定指标，而协整分析的核心算法是求解残差乘积矩的特征值问题，直接取协整残差作为损伤判定指标。因此，两种方法具有一定的相似性。

3 稳定性评价

基于主成分分析和协整分析的损伤判定方法本质上是一种二元分类器，即将结构响应数据分类为“阴性”和“阳性”，其中“阴性”代表正常状态，“阳性”代表损伤状态。分类器的鲁棒性通常可用受试者工作特征曲线(receiver operating characteristic curve，ROC)来衡量。给定某一阈值水平η，分别记录损伤状态下残差超出阈值范围的样本数目，即真阳性样本数目TP；损伤状态下位于阈值范围之内的样本数目，即假阴性样本数目FN；正常状态下残差超出阈值范围的样本数目，即假阳性样本数目FP；正常状态下位于阈值范围之内的样本数目，即真阴性样本数目TN，最终组成如表1所示的混淆矩阵。基于此，我们可以计算该阈值水平下阴性样本被判定为阳性的比例，即假阳性率FPR(η)；以及阳性样本被判定为阳性的比例，即真阳性率TPR(η)

表1 混淆矩阵Tab.1 Confusion matrix

(34)

(35)

使阈值水平η在从0变化到+∞，我们可以得到体现该分类器性能的ROC。为了便于描述，通常通过计算ROC的面积进行说明。当ROC位于曲线y=x附近，即当其所围面积约为0.5时，表明该分类器等同于随机试验，已不具备判别能力；ROC所围面积越接近1，表明该分类器鲁棒性越好。

然而，直接使用ROC对分类器的性能优劣进行评价是不严谨的，不同的测试数据将产生不同的ROC，因此通过方差进行度量才能更准确地反映出分类器性能的优劣[23]。方差的获取可通过对多个测试数据集取平均实现，常用的有垂直平均法和阈值平均法。

3.1 垂直平均法

垂直平均法通过给定假阳性率FPR的采样间隔，对多条ROC在对应的假阳性率FPR采样点处的真阳性率TPR取平均，并记录相应的标准差。对于某一特定的FPR采样点，当ROC上不存在对应的真阳性率TPR时，可通过相邻的两个假阳性率FPR对应的TPR插值获取。

3.2 阈值平均法

垂直平均法的优点在于其平均值由因变量TPR组成，这简化了置信区间的计算。然而，ROC的自变量FPR往往不是人为控制的。而阈值平均法使独立变量人工可控。该方法根据产生ROC上的点的阈值进行采样，然后为每个阈值找到每条ROC的对应点，再分别关于对应ROC点的FPR和TPR取平均。因此，阈值平均法将产生垂直和水平两个方向的方差。

4 数值模拟

4.1 海洋平台模型

本文以一个导管架平台模型为例，比较主成分分析与协整分析的性能差异。主要考虑了环境温度对结构频率的影响。结构频率通过MATLAB软件求取结构的特征方程获得。

导管架平台有限元模型简图，如图1所示。此模型划分为80个单元，48个节点。结构的材料密度ρ=7 850 kg/m3，泊松比μ=0.3。平台总质量为550 t，其中上部荷载为250 t，为简化模拟，将上部载荷简化为质量单元平均分配到平台顶层的4个节点上。平台顶层和底层尺寸分别为6.097 m×5.284 m和10.112 m×8.764 m。平台各杆件尺寸，如表2所示。该平台作业海域水深22 m，取泥面以下9 m为简化固定端。

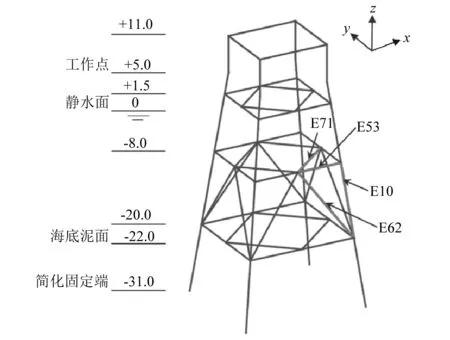
图1 导管架平台模型(m)Fig.1 Sketch of the offshore platform structure(m)

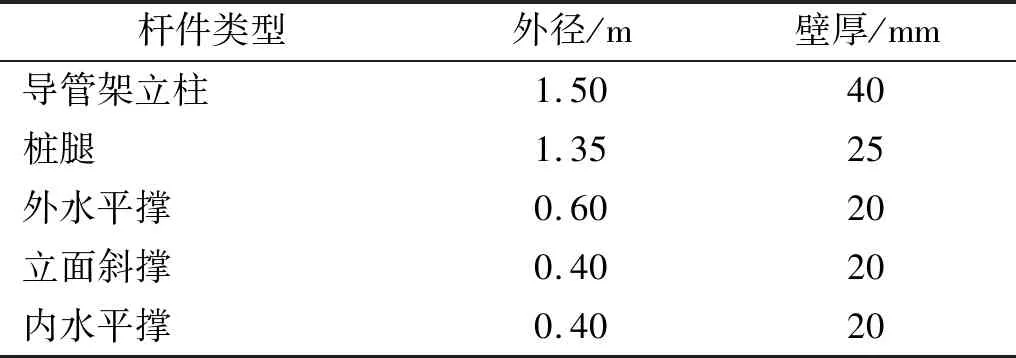
表2 平台各杆件尺寸Tab.2 Member dimensions of the offshore platform

4.2 温度对结构频率的影响

温度对结构频率的影响是通过改变结构材料的弹性模量实现的。根据Woon等[24]的研究结果，钢材弹性模量与环境温度之间存在以下线性关系

En(κν)=(1+cv)En(κ0)

(36)

式中，En(κ0)和En(κν)分别为参考环境温度κ0和当前环境温度κν下单元n的弹性模量。本文取参考环境温度κ0为20 ℃，对应的材料弹性模量为206 GPa。变化系数取为cv=c0(κν-κ0)/En(κ0)，c0=-1.0×108N/m2·°C。环境温度与钢材弹性模量的关系，如图2所示。

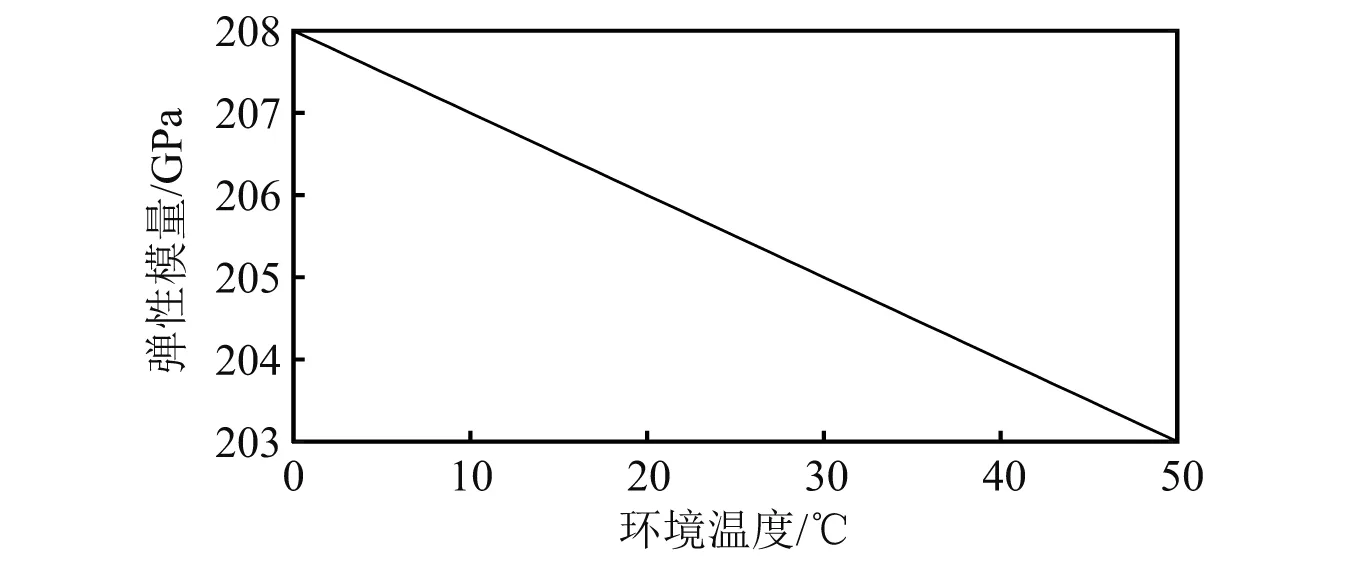
图2 环境温度与钢材弹性模量的关系Fig.2 Relationship between steel elastic modulus and ambient temperature

4.3 工况分析

海洋平台结构位于空气、海水和海底泥土3种介质中，3种介质的传热性质差异较大，其温度变化不尽相同。本文采用了某海洋观测站实测的温度变化数据，数据记录了该海域每小时的气温、水温和海底以下5 m的泥温，截取了4 000组温度变化的数据以模拟结构频率的变化，3种环境温度的变化曲线，如图3所示。其中，1～3 500组温度用于模拟正常状态下结构的频率变化，作为基准数据；3 501～4 000组温度用于模拟各损伤工况下结构的频率变化，作为测试数据。损伤工况设置，如表3所示，其中工况A为健康工况，用于探究方法是否会发生损伤误判，工况B～工况E为损伤工况，分别模拟平台内水平撑单元、外水平撑单元、立面斜撑单元以及立柱单元的损伤，用于探究方法是否会发生损伤漏判，结构损伤通过对相应单元进行刚度削减来模拟。图4给出了结构前3阶频率的模拟结果，其中1～3 500组作为基准数据，3 501～6 000组以每500组为一个工况，分别对应工况A～工况E。可以看出，温度变化在一定程度上掩盖了结构损伤导致的结构频率变化，为了避免损伤误判和损伤漏判的发生，有必要消除温度变化的影响。

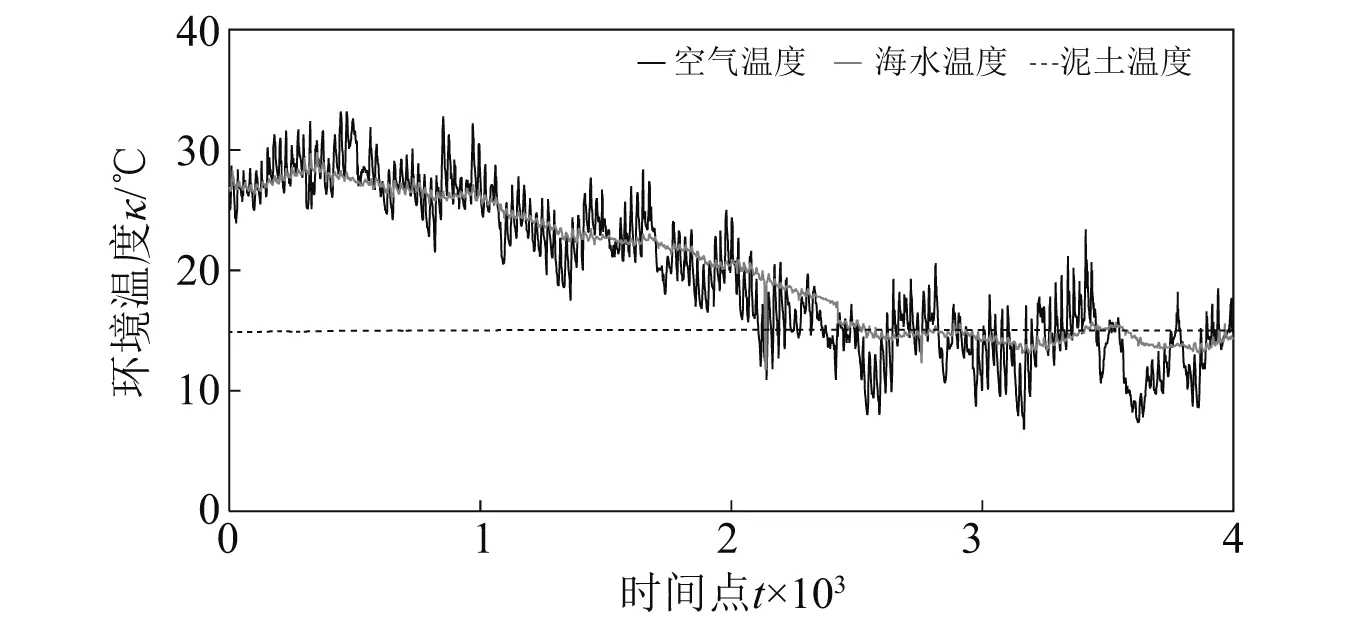
图3 实测温度变化曲线Fig.3 Measured temperature history series

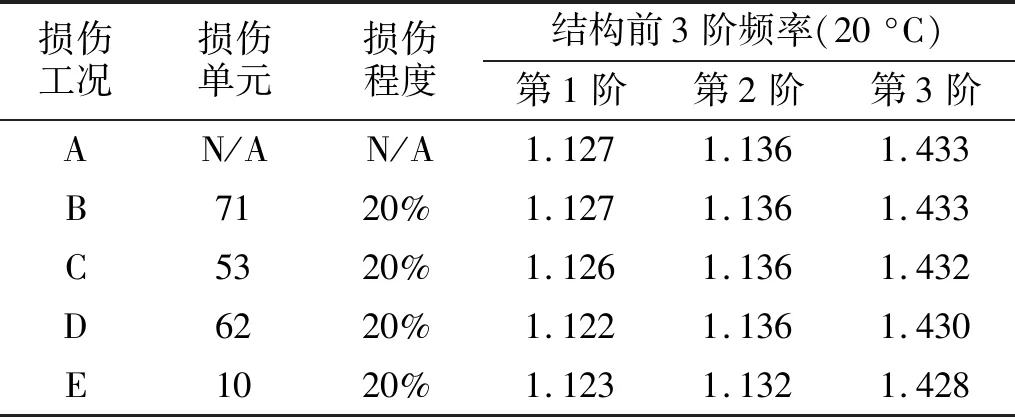
表3 模拟的海洋平台损伤工况Tab.3 Simulated damage cases of the offshore platform

图4 结构前3阶频率Fig.4 First three natural frequencies under temperature changing

提取前3阶频率的3 500组基准数据，分别进行主成分分析和协整分析，所得主成分转换矩阵T和协整向量β将用于各损伤工况的判定。其中，主成分分析的能量阈值取为0.95，由表4可知选取的主成分阶数为1。协整秩检验的显著性水平取为0.01，参见表5。首先假设r=0，根据式(29)计算得到LR统计量为75.641 0>41.072 2，拒绝原假设。进一步假设r=1，此时统计量为16.075 5<23.157 4，接受原假设，因此频率数据存在一个协整关系。可见，温度影响这一“共同趋势”起了主要作用。

表4 主成分阶数的选取Tab.4 Selection number of principle components

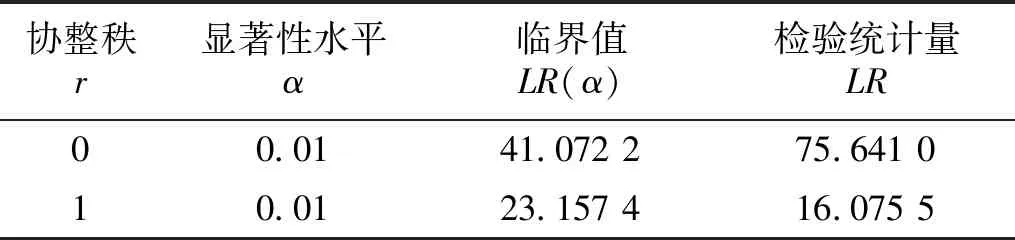
表5 协整秩检验Tab.5 Hypothesis test of cointegration rank

为方便比较，将主成分残差dt与协整残差ξt均作最大值归一化处理。由图5及表6、表7可以看出：对于工况A，两种算法的异常值比例均远小于10%，残差均值比均小于1.5，其判定结果为结构没有发生损伤，与实际情况一致。对于工况B，两种算法的异常值比例均小于10%，残差均值比均小于1.5，未能准确识别出损伤，主要原因是单元71为内水平撑，其刚度损失对结构整体刚度的变化几乎没有影响，以至于损伤工况B对结构频率的变化影响甚微，因此导致了两种算法均出现了漏判。对于工况C～工况E，两种算法的异常值比例均为100%，残差均值比远大于1.5，完全准确地识别出结构损伤。对比来看，工况A下两种算法的残差均值比均在1.1附近，差别并不明显。对于工况C～工况E，协整分析对应的残差均值比明显较高，说明该算法在察觉结构频率的异常数据方面具有更高的灵敏度。

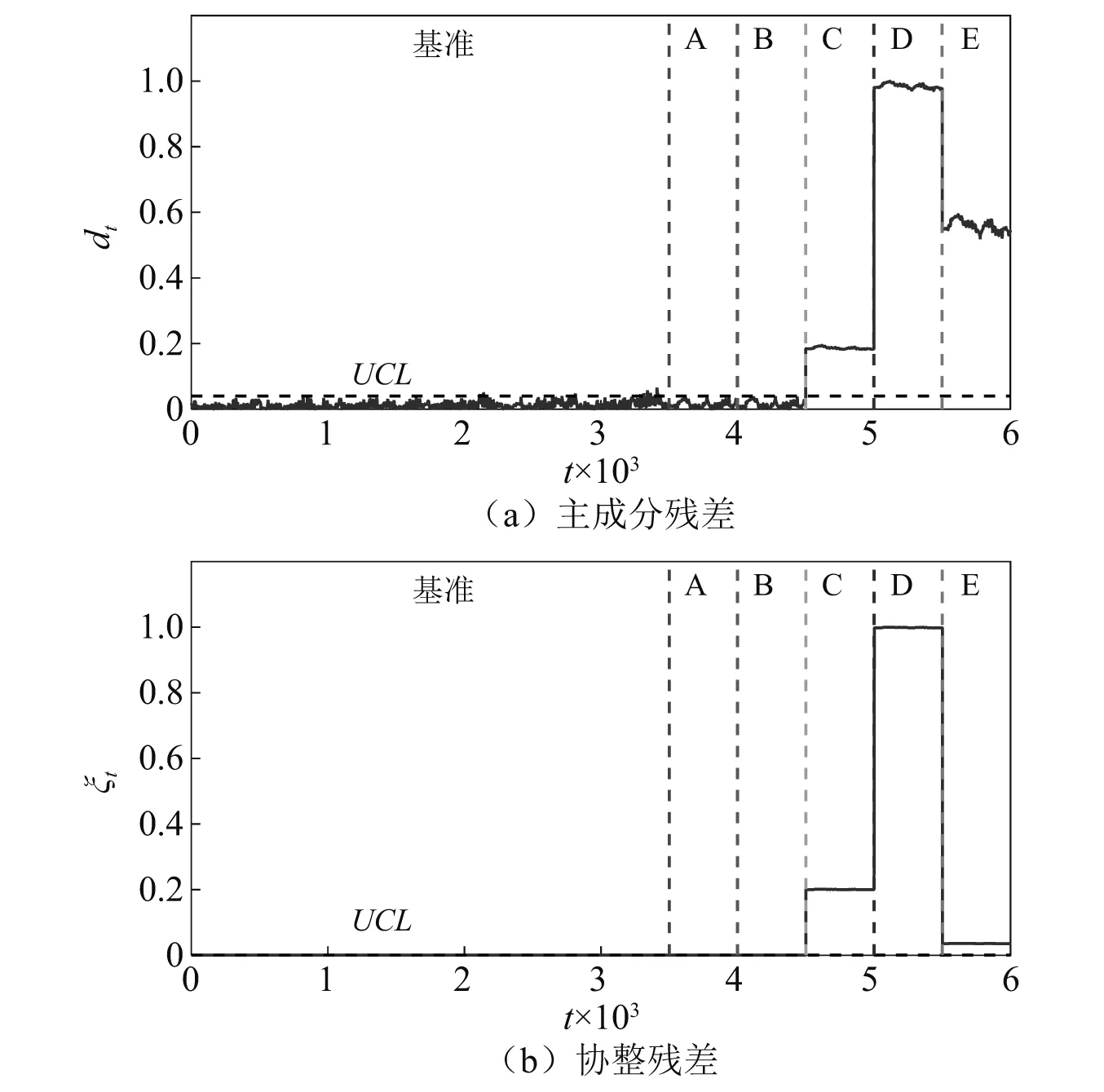
图5 各损伤工况判定结果Fig.5 The damage detection results of damage case A to damage case E

表6 各工况异常值比例Tab.6 Outliners ratio in each case %

表7 各工况残差均值比Tab.7 Mean value ratio of residuals

由于工况B～工况E对应不同的杆件类型发生相同程度的损伤，因此其残差均值比的大小代表了两种算法对不同杆件类型损伤的灵敏度。由表7可以看出，对于主成分分析，不同杆件类型的损伤检测灵敏度从高到低依次为：立面斜撑>立柱>外水平撑>内水平撑；对于协整分析，不同杆件类型的损伤检测灵敏度从高到低依次为：立面斜撑>外水平撑>立柱>内水平撑。可见，两种算法均对立面斜撑的损伤最为灵敏。对比立柱和外水平撑两种杆件的损伤，若采用主成分分析，则立柱的损伤更容易识别；若采用协整分析，则外水平撑的损伤更容易识别。因此，实际检测过程中可根据目标检测杆件的不同采用不同的方法。

4.4 算法的噪声鲁棒性

实际频率识别过程中还不可避免的受到系统和量测噪声等不确定性因素的干扰，参考梁亚斌等的做法，本文采用以下噪声模型

(37)

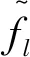
仍以结构前3阶频率作为样本数据，设定某一噪声水平，通过一次模拟，得到噪声影响下的一组频率样本，通过改变X-bar图的阈值控制线，得到该频率样本下的ROC(PCA和CA各对应一条ROC)。将以上模拟重复1 000次，得到1 000条ROC，对曲线取垂直平均，则可得到某一噪声水平下的平均ROC。以下取工况A的频率样本作为阴性样本，工况C的频率样本作为阳性样本，测试两种算法的噪声鲁棒性。其中假阳性率FPR的采样间隔取为0.002。由图6和表8可以看出，当噪声水平为5%时，协整分析对应的平均ROC面积更接近于1，且其1 000次模拟得到的ROC面积的标准差相对更小，说明其鲁棒性更好。但随着噪声水平的增加，主成分分析对应的平均ROC面积更接近于1，且其ROC面积的标准差相对更小，因此其鲁棒性更好。

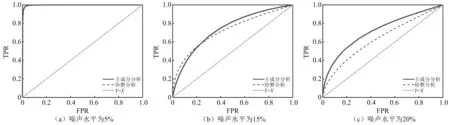
图6 工况C平均ROCFig.6 The averaging ROC curves of case C

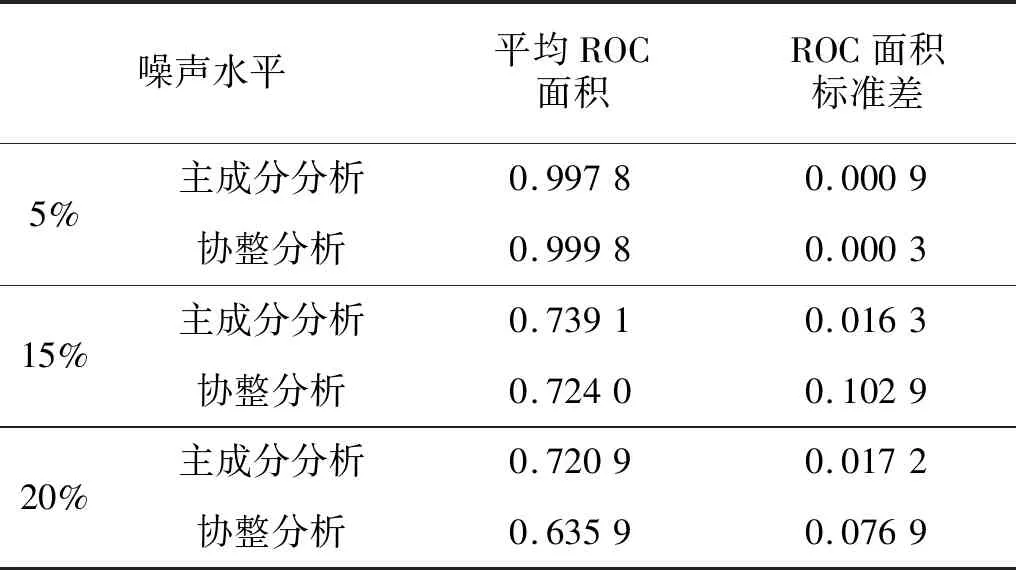
表8 工况D平均ROC所围面积及标准差Tab.8 Standard deviation of the area under ROC

4.5 基准样本数目的影响

由于主成分分析的投影矩阵T和协整分析的协整向量β是通过基准数据得到的，因此基准数据的样本数目对算法的性能会造成一定的影响。取结构前3阶频率作为样本数据，设定某一噪声水平，改变基准数据的样本数目N，求解该基准样本数目对应的投影矩阵T和协整向量β以用于损伤工况的判定。仍取工况A的频率样本作为阴性样本，工况C的频率样本作为阳性样本，以1.2节定义的上控制线UCL作为阈值控制线，记录相应的假阳性率FPR。由于假阳性率代表了损伤误判的概率，因此应尽可能的小。考虑到噪声的随机性，将以上模拟重复1 000次，并对相应的FPR取平均，则可得到FPR随基准样本数目N变化的曲线。由图8可以看出，对于噪声水平为10%的情况，当基准样本数目为500～1 200时，主成分分析对应的假阳性率大于0.96，误判较为严重，而协整分析对应的假阳性率小于0.21，误判率较低。对于噪声水平为15%的情况，当基准样本数目为500～1 500时也有类似的现象。以上说明了在一定的噪声水平下，当基准样本数目较小时，协整分析可以更加有效地抑制损伤误判的问题。

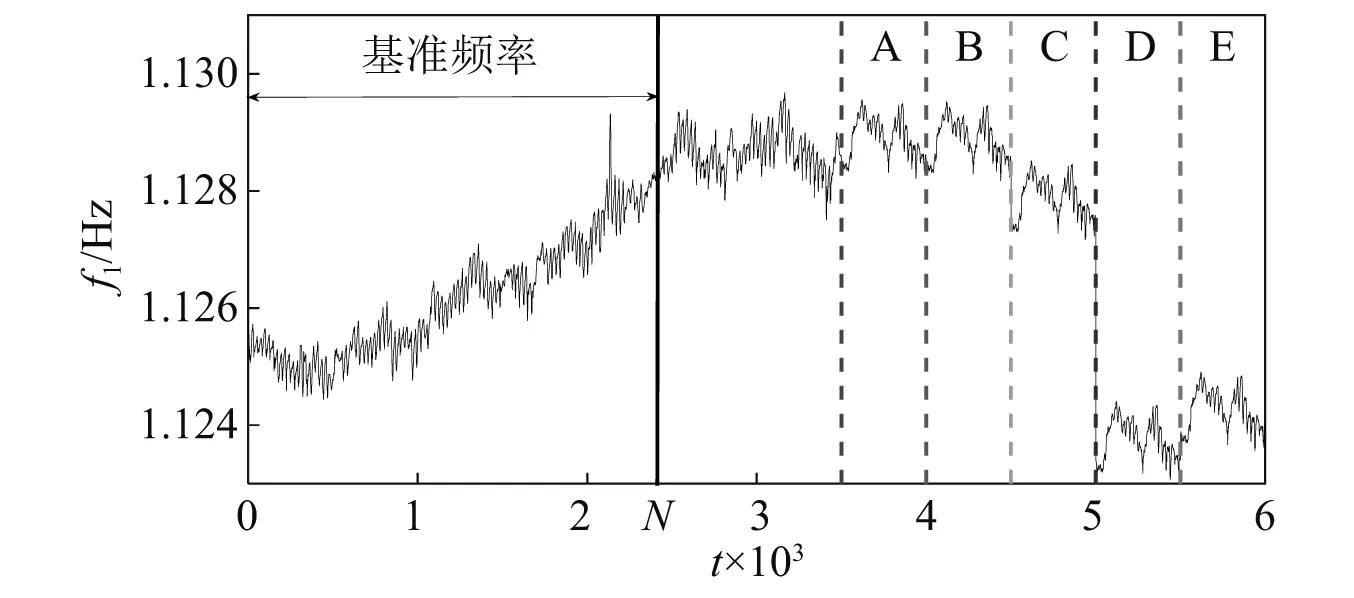
图7 基准频率的选取(以第1阶频率为例)Fig.7 Baseline natural frequencies selection(the 1st frequency as an example)

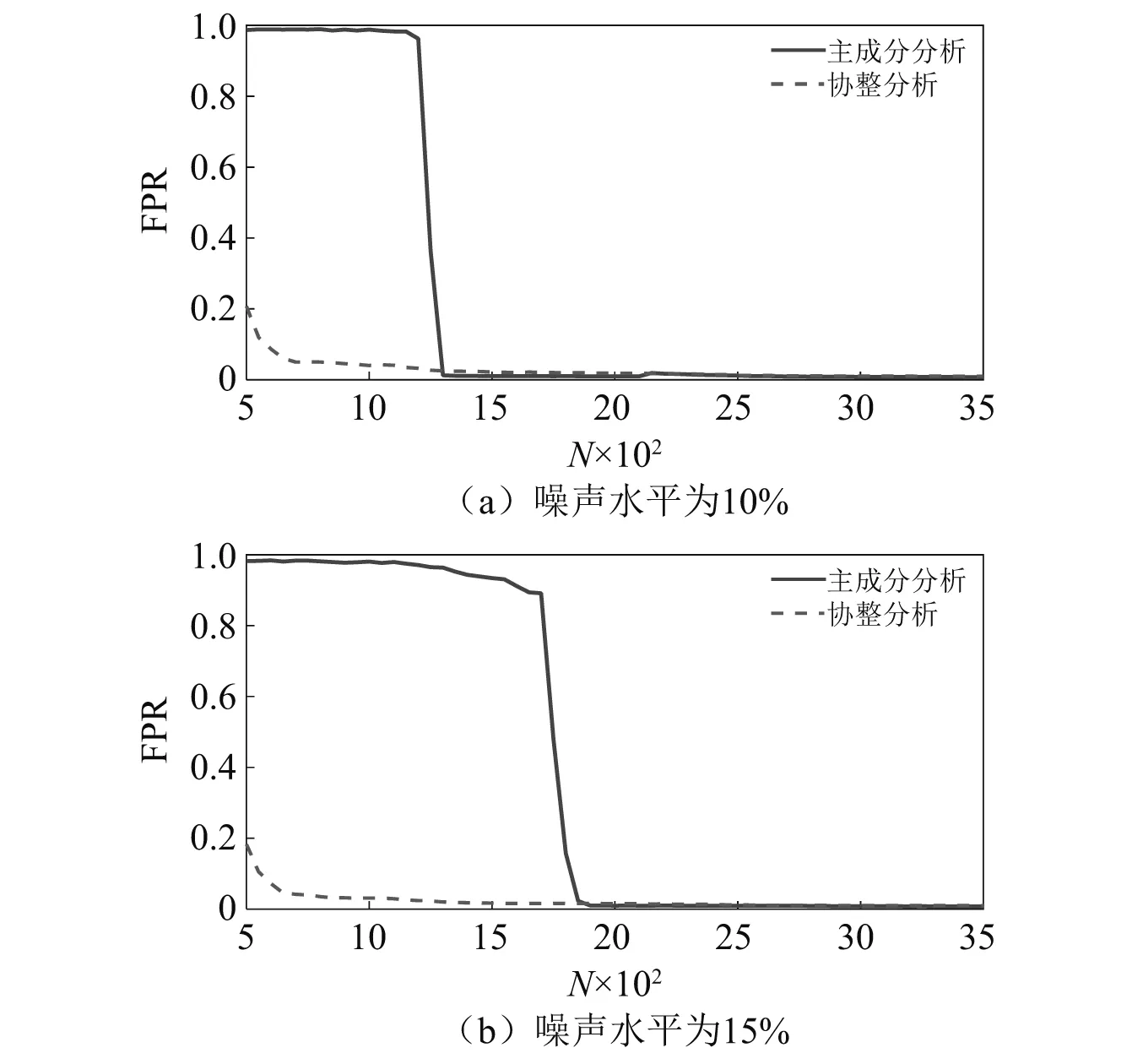
图8 假阳性率随基准样本数目的变化曲线Fig.8 Curves of FPR changing with sample number of baseline natural frequencies

5 结 论

本文以一个海洋平台模型为例，考虑了空气、海水和海底泥土温度变化的影响。以结构的模态频率作为样本数据，分别利用主成分分析和协整分析消除温度变化影响，提取能够表达结构真实特性的主成分残差和协整残差，继而根据X-bar控制图并结合结构损伤前后的残差均值比进行损伤判定。通过改变频率数据的噪声水平以及基准样本的数目，比较分析了两种方法的性能差异。结果表明：

(1)两种方法均能有效消除环境温度的影响，避免损伤误判和损伤漏判的发生。在不考虑噪声的条件下，各损伤工况对应的协整残差均值比更大，说明协整分析具有更高的损伤检测灵敏度。

(2)小噪声水平下(噪声水平小于5%)，协整分析对应的平均ROC所围面积更接近1，且其ROC面积的标准差相对更小，因此其鲁棒性更好。随着噪声水平的增加，主成分分析的噪声鲁棒性更好。

(3)在一定的噪声水平下，当基准频率样本数目较小时，主成分分析对应的假阳性率较高，误判严重；协整分析对应的假阳性率较低，可更加有效地抑制损伤误判的问题。