联合噪声激励下分数阶三稳van der Pol振子的随机P分岔
2021-09-27李亚杰吴志强兰奇逊张祥云
李亚杰,吴志强,兰奇逊,郝 颖,张祥云
(1.河南城建学院 数理学院,河南 平顶山 467036;2.天津大学 机械学院,天津 300072;3.天津市非线性动力学与混沌控制重点实验室,天津 300072;4.燕山大学 建筑工程与力学学院,河北 秦皇岛 066004;5.天津中德应用技术大学 基础课部,天津 300350)
分数阶导数是对整数阶导数的推广,将函数的求导阶次从传统的整数阶扩展到了非整数阶的情形,至今已有三百多年的发展历史。由于整数阶导数定义的局限性,其不能表达黏性物质的记忆特性,而分数阶导数定义含有卷积部分,能很好地表达记忆效果,表示出随时间累积的效应,因而与传统的整数阶微积分系统相比,含分数阶微积分的系统更具有优越性,是描述记忆特征的恰当数学工具[1-4]。近年来,关于分数阶微积分及其应用的研究引起了不同领域科研人员的广泛关注,已成为研究反常扩散、多孔介质力学、非牛顿流体力学、黏弹性力学、软物质物理等学科领域的有力数学工具。由于分数阶导数能更准确的描述各种反应变化过程,很多问题可以用分数阶微分方程来更好地描述[5-9],因而研究分数阶微分方程中的典型力学特性和分数阶参数对系统的影响也是十分必要和有着重要意义的。
近年来相关学者研究了在不同噪声激励下非线性多稳态系统的动力学行为,取得了丰硕的成果:整数阶系统方面,文献[10-14]研究了Duffing-van der Pol振子在Lévy噪声、色噪声、谐和与随机噪声联合激励下系统响应的稳态概率密度问题,通过分析系统稳态概率密度函数性质的变化,讨论了噪声振子的随机P分岔现象,得到了系统双峰概率密度函数的解析表达式,结果表明系统参数与噪声强度均能诱导系统发生随机P分岔行为。Wu等[15]利用奇异性理论研究了一、三稳态van der Pol-Duffing振子在乘性色噪声激励下系统稳态响应的随机P分岔行为,得到了系统幅值稳态概率密度函数的表达式,分析了系统参数及噪声强度对系统随机P分岔的影响;分数阶系统方面,Chen等[16]研究了谐和与宽带噪声联合激励下含分数阶导数阻尼Duffing振子的响应,发现分数阶导数阶次的变化可以导致系统发生随机P分岔。Huang等[17]讨论了分数阶单自由度非线性系统在高斯白噪声激励下的响应和稳态概率密度函数。Yang等[18]应用Zhuravlev非光滑变换和随机平均法研究了高斯白噪声激励下含Caputo型分数阶阻尼的非线性碰撞振动系统的随机分岔。Li等[19]研究了在加性及乘性色噪声激励下含分数阶导数的广义Duffing-van der Pol系统的双稳态随机分岔现象,发现线性阻尼系数、分数阶导数阶次及噪声强度的变化均可导致系统发生随机P分岔行为。
由于分数阶导数的复杂性,其分析方法也变得更加困难,系统参数对振动特性的研究多限于定性分析,未能找出参数影响的临界条件,影响此类系统的分析和设计,且目前关于三稳态分数阶系统的随机P分岔问题,还未见报道。针对以上情况,本文以联合噪声激励下广义van der Pol方程的非线性振动为例,用奇异性方法求得分数阶系统的转迁集曲线,得到了系统发生随机P分岔的临界参数条件,并分析了转迁集参数平面内各区域中系统幅值稳态概率密度的曲线类型。通过Monte Carlo模拟的方法,将所得数值结果与文中求得的解析结果进行了比对,可以看出数值解与解析解的吻合情况较好,从而验证了本文理论分析的正确性。
1 等价系统的推导
关于分数阶导数的定义较多,常用的有Riemann-Liouville导数和Caputo导数,但Riemann-Liouville导数对应的初始条件没有物理意义,而Caputo导数所描述系统的初始条件有着清楚的物理意义且形式上和整数阶微分方程的初始条件类似,故在本文中我们采用Caputo导数。定义在区间[a,b]上的函数x(t)的p阶Caputo导数定义为
(1)
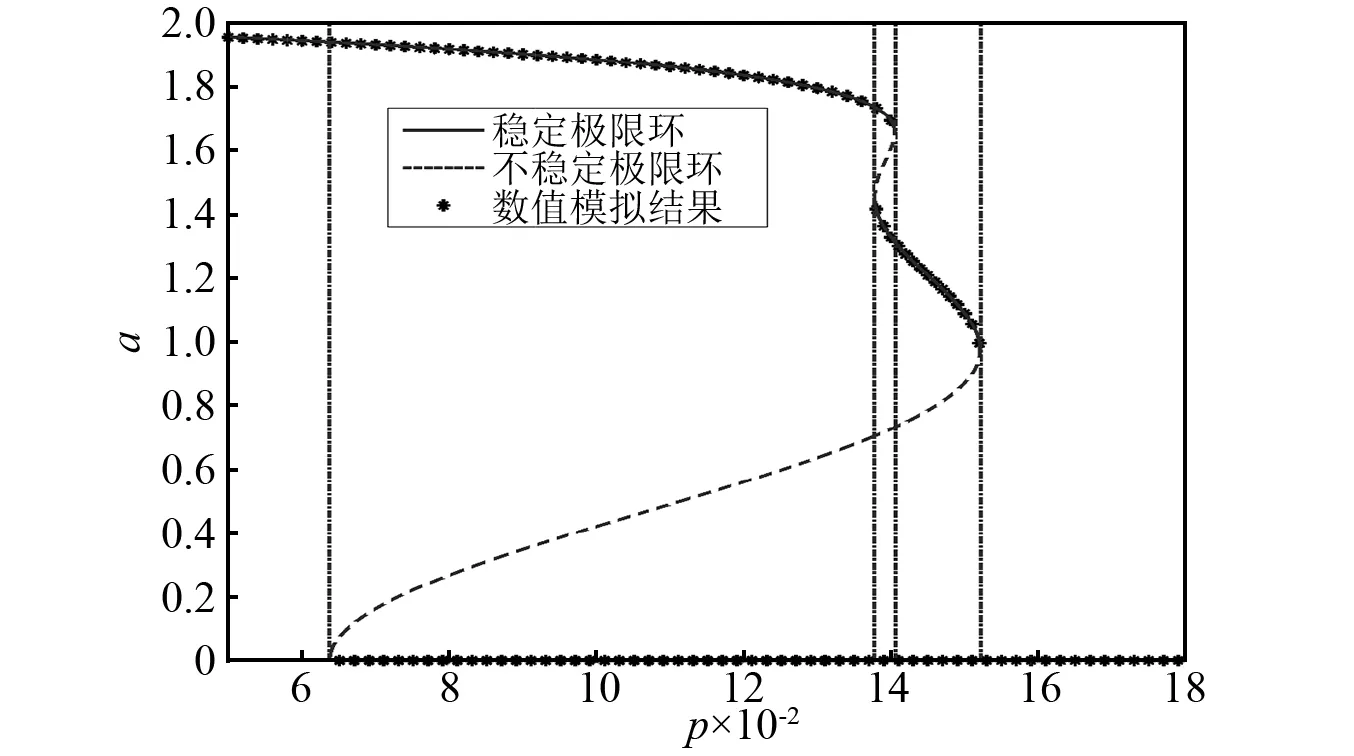
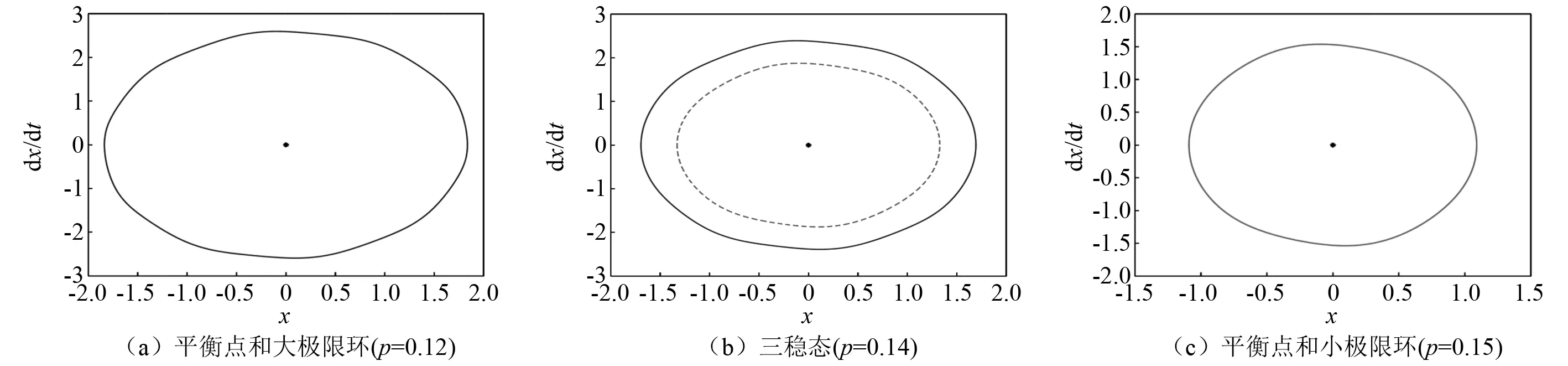
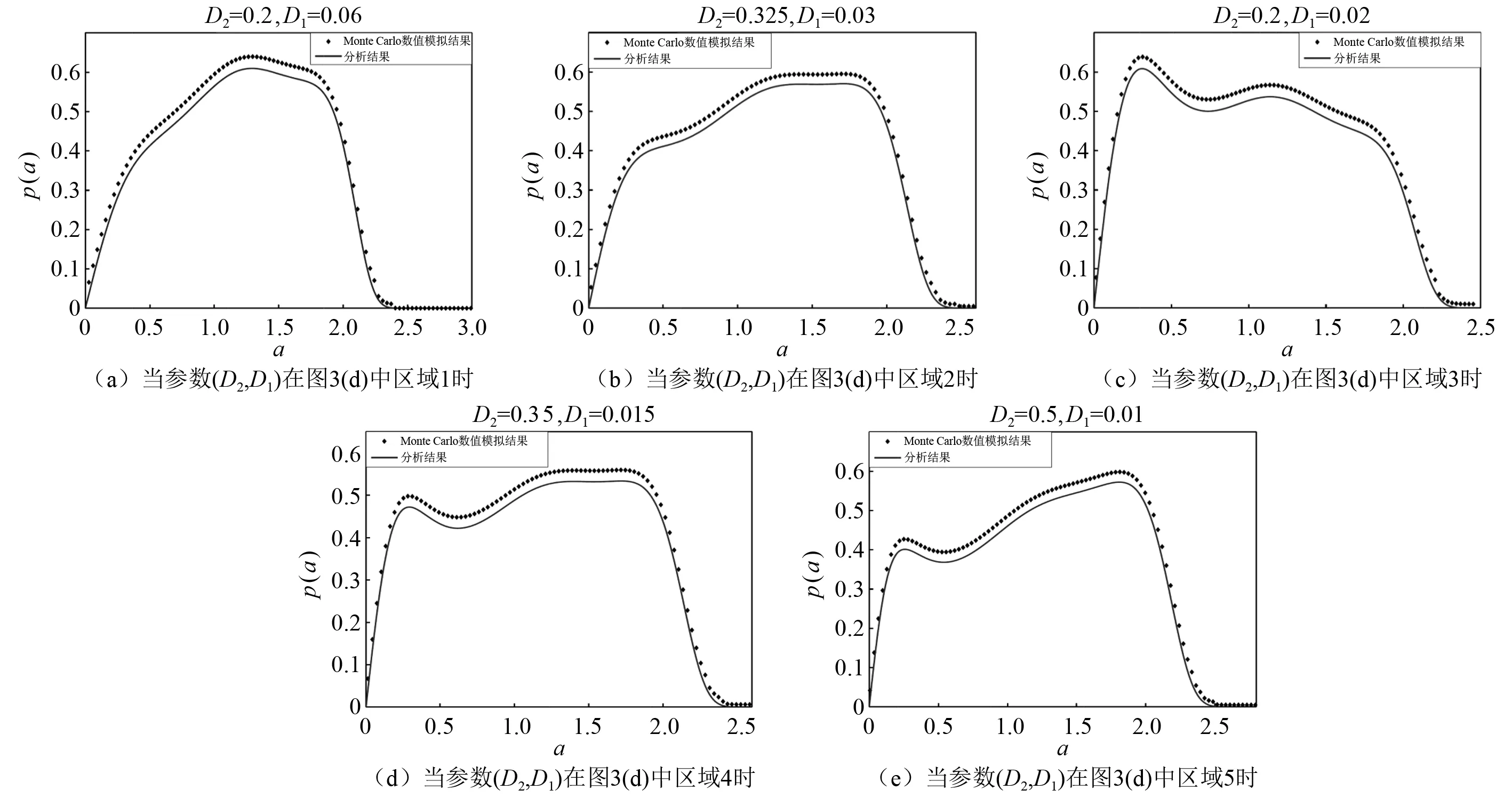
式中:m-1 (2) 式中,m-1 本文研究联合噪声激励下含分数阶导数项的广义van der Pol系统 ξ1(t)+x(t)ξ2(t) (3) E[ξk(t)]=0,E[ξk(t)ξl(t-τ)]=2Dklδ(τ) (4) 由文献[20-23],分数阶导数项可以等效为阻尼力和回复力的线性组合,故引入以下的等效系统 [K(p,w)+w2]x=ξ1(t)+x(t)ξ2(t) (5) 式中,C(p,w),K(p,w)分别为等效阻尼力和回复力的系数。 式(3)和式(5)的误差为 (6) 由均方误差最小的必要条件[24] (7) 将式(6)代入式(7)中可得 (8) 式(3)的解可设为如下形式 x(t)=a(t)cosφ(t) (9) 式中,φ(t)=wt+θ。 则有 (10) 将式(9)、式(10)代入式(8),并关于φ进行积分平均可得 (11) 从而,等价式(5)可以表示为以下形式 (12) 其中 (13) 对于式(12),取定线性及非线性阻尼的系数分别为ε=-0.1,α1=1.51,α2=2.85,α3=1.693,α4=0.312,w=1,为方便讨论参数影响,图1给出了当D1=D2=0时,对应的确定性系统极限环幅值随分数阶导数阶次p变化的分岔曲线。 图1 确定性系统分岔图Fig.1 Bifurcation diagram of the deterministic system 可以看出,当p在区间[0.063 7,0.137 7]变化时,系统有2个吸引子:平衡点和大极限环,如图2(a)所示;当p在区间[0.137 7,0.140 6]变化时,系统有3个吸引子:平衡点、小极限环和大极限环,如图2(b)所示;当p在区间[0.140 6,0.152 2]变化时,系统有2个吸引子:平衡点和小极限环,如图2(c)所示。 图2 相图Fig.2 Phase portraits 为求解式(12)响应幅值的稳态概率密度函数,引入如下变换[25] (14) 式中,a(t),θ(t)分别为系统的幅值和初始相位,均为随机过程。 将式(14)代入式(12),由确定性平均法可得 (15) 其中, (16) 式(15)可以被看作Stratonovich随机微分方程,通过加入相应的Wong-Zakai修正项,可以将其转化为如下的It随机微分方程 (17) 式中,Bk(t)(k=1,2)为标准的维纳过程,且 (18) 对式(17)关于Φ进行随机平均[26],可得如下的平均It方程 (19) 式中,B1(t)与B2(t)为2个相互独立的单位Wiener过程,且 (20) 式(20)表明,振动幅值a(t)的平均It微分方程与θ(t)是相互独立的,故a(t)为一维的随机过程。振动幅值a(t)的FPK方程可表示为 (21) 其对应的边界条件为 (22) 基于以上边界条件,式(21)的稳态解即为系统幅值的稳态概率密度函数 其中,C为归一化常数,满足 将式(20)代入式(23),可得振动幅值a稳态概率密度函数的具体表达式 (25) 其中, (26) 随机P分岔是指概率密度函数曲线峰值数目的变化,为得到P分岔的临界参数条件,以下从奇异性分析的角度来分析参数变化对系统随机P分岔的影响。 为方便起见,p(a)可表示为 p(a)=4CR(a,D1,D2,ε,w,p,α1,α2,α3,α4)exp[Q(a,D1,D2,ε,w,p,α1,α2,α3,α4)] (27) 其中, (28) 根据奇异性理论[27],概率密度函数需满足如下的2个条件 (29) 将式(27)代入式(29),可得如下条件 H={R′+RQ′=0,R″+2R′Q′+RQ″+RQ′2=0} (30) 式中,H为概率密度函数曲线峰值数目变化的条件。 由于参数关系在三维曲面中不容易刻画和显示,这里我们只给出转迁集的二维截面来表示噪声强度和分数阶导数阶次的影响。 根据图1中确定性吸引子的分布,不失一般性,我们分别在系统单稳态、双稳态及三稳态区间内取定分数阶导数阶次p的值,并根据式(28)及式(30)计算联合噪声激励下系统对应的转迁集。由于当分数阶导数阶次p在区间[0,0.063 6]中取值时,系统转迁集为空集,因此我们仅在区间[0.063 7,0.137 7]中取(a)p=0.1,区间[0.137 8,0.140 5]中取(b)p=0.14,区间[0.140 6,0.152 2]中取(c)p=0.15及区间[0.152 3,0.18]中取(d)p=0.17,具体转迁集分别如图3所示。 为便于比较分析,以上在转迁集各区域中均用数字进行了标注,数字标号相同的区域表示系统幅值稳态概率密度曲线是定性相同的,方便起见,我们仅对转迁集图3(d)各子区域中系统幅值的稳态概率密度曲线进行分析,将所得解析结果与式(1)的Monte Carlo数值模拟结果进行对比,具体结果如图4所示。 图3 不同分数阶导数阶次p下的转迁集(以D2和D1为开折参数)Fig.3 Transition sets under different values of fractional derivative’s order p(taking D2 and D1 as the unfolding parameters) 图4 图3(d)不同子区域中幅值的概率密度函数p(a)Fig.4 PDF of amplitude p(a)in different sub-areas of Fig.3(d)(taking D2 and D1 as the unfolding parameters) 由图3(d)可见:概率密度曲线出现多峰的参数区域由2个近似三角形区域围成,特别地,二者重合的区域4构成了系统幅值稳态概率密度曲线的三峰区域。当参数在(D2,D1)参数平面区域1中取值时,概率密度曲线在离原点较远处有一明显峰值,如图4(a)所示;当参数在区域2中取值时,概率密度曲线在离原点较远处有2个区分不明显的峰值,系统同时存在大、小极限环,如图4(b)所示;当参数在区域3中取值时,概率密度曲线在离原点较远处仍有一明显峰值,但在原点附近概率明显不为0,系统同时存在平衡点与大极限环,如图4(c)所示;当参数在区域4中取值时,概率密度曲线在原点以外还存在2个峰值,系统表现为平衡点与大、小极限环共存,如图4(d)所示;当参数在区域5中取值时,概率密度曲线与区域3中定性相同,概率密度曲线偏离原点的峰值所对应的幅值a要小于图4(c)中峰值所对应的a值,系统同时存在平衡点与小极限环,如图4(e)所示。 以上分析结果表明,分数阶导数阶次p的取值不同,其对应的联合噪声下的转迁集图形亦不相同,这意味着,分数阶导数项的加入能对系统幅值稳态概率密度起到调控的作用,可以从分数阶导数阶次p、加性噪声强度D1及乘性噪声强度D23个方面来控制联合噪声作用下系统的运动形式。图3中任意相邻的2个区域所对应系统幅值的稳态概率密度曲线是定性不同的,参数(D2,D1)的取值越过图3中任意一条线,系统均将发生随机P分岔行为,故转迁集曲线即为系统发生随机P分岔的临界参数条件,且图4中解析结果与Monte Carlo数值模拟结果吻合较好,这也进一步验证了本文理论分析的正确性。 本文对联合噪声激励下含分数阶导数项的广义van der Pol系统的三稳态随机P分岔现象进行了研究。根据均方误差最小原则,将原系统转化为了等价的整数阶系统,运用随机平均法得到了系统幅值的稳态概率密度函数。并利用奇异性理论,得到了系统发生随机P分岔的临界参数条件,通过选择合适的开折参数,可使系统响应维持在单稳态或平衡点附近小幅振动,可避免系统发生大幅振荡或非线性跳跃现象造成失稳,可为相关系统设计提供理论指导。对原系统进行Monte Carlo数值模拟验证了所得理论结果的正确性,分析得出:分数阶导数阶次p及噪声强度D2,D1均可引起系统发生随机P分岔行为,通过选取相应的参数p及(D2,D1)可以实现系统幅值稳态概率密度曲线峰值1~3的变化。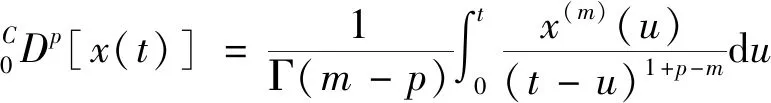
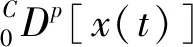
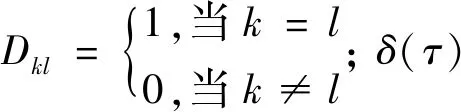
2 幅值的稳态概率密度
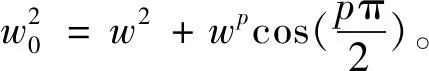
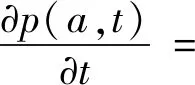
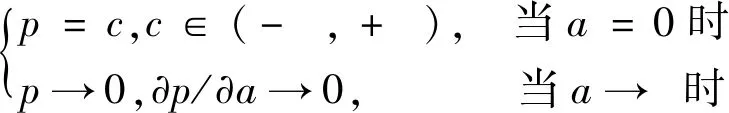
3 随机P分岔
4 分数阶导数阶次p对系统随机P分岔行为的影响

5 结 论
