基于经验小波变换的振动信号特征量提取

王 茜，田慕琴，宋建成，贺 颖，冯君玲，吝伶艳

(1.太原理工大学 矿用智能电器技术国家地方联合工程实验室,太原 030024；2.太原理工大学 煤矿电气设备与智能控制山西省重点实验室,太原 030024)

岩巷掘进机由于其有截割能力强等优点成为我国煤岩巷道开采的主要设备[1]。但是由于掘进机工作环境恶劣，司机视野受限，传统掘进机智能化水平偏低，司机无法根据掘进机状态及时准确地调整截割头各项参数，导致掘进机截齿受损，功率超限，寿命降低，因此提高掘进机智能化水平变得尤为重要[2]。截割头动载荷识别是实现掘进机智能化的必要前提，而载荷的变化势必会引起截割头振动信号的变换，因此，通过对振动信号的变化分析可以完成掘进机动载荷的识别[3]。

特征提取是掘进机截割头振动信号分析的重要一步，可以对掘进机所切割岩壁的硬度进行明显划分[4]。近年来，常用的振动信号提取方法主要以小波包分解为基础进行变换。然而这些方法虽在一定程度上实现了掘进机振动信号去噪与特征量提取，并取得了较好的效果，但很大程度是依赖于最优小波基函数以及信号分解层数的选择[5]，且当信号幅值发生剧烈变化时，具有很大的局限性[6]。

经验小波变换(empirical wavelet transform，EWT)是由Gilles基于小波变换和窄带信号分析理论提出来的，通过建立自适应小波滤波器组来提取信号幅度和频率调制分量[7]。近年来，通过国内外学者的不断研究，该方法以其计算方便等优点被广泛应用于各个领域。

在实际工作中，掘进机截割头切割岩壁时，岩壁硬度并不是一成不变的。不同岩壁硬度下掘进机的振动信号差异较大，所以需要对不同硬度下的振动信号进行分析并提取其特征量。针对以往掘进机截割头振动信号分析方法的不足，本文提出了一种基于EWT和相关性阈值去噪相结合的信号特征提取方法。首先对不同岩壁硬度下的振动信号进行EWT分解，对各个分量进行相关性阈值去噪处理，此后计算各分量与原始信号之间的相关系数，选择相关性较高的分量构成振动信号的特征矢量。

1 经验小波变换

1.1 经验小波变换原理

经验小波变换是一种经验模态分解原理与小波框架理论相结合的分析方法[8-11]。他通过小波框架理论构造滤波器组，自适应地将信号分解一系列频率由高到低排列的AM-FM分量，从而提取特征量。经验小波变换原理如下。

步骤1对信号f(t)进行傅里叶变换得到其对应的频谱f(w)。

步骤2根据信号的频谱图，查找f(w)的局部极大值点并依次降序排列。根据极大值点对信号的频域进行分段，取相邻两个极大值点间的中间数值作为频域分界点wn(n=1,2,…)。

步骤3根据步骤2中的频率分段构造经验小波的小波函数ψn(w)和尺度函数φn(w)，其表达式为

(1)

(2)

其中部分参数的计算方法为

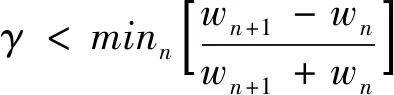
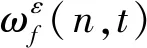
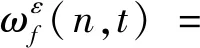
(3)

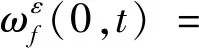
(4)

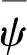
对信号进行重构，结果为

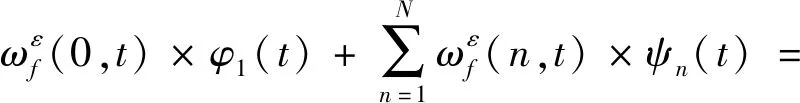
(5)

最终得到原始信号的经验小波函数为

(6)

(7)

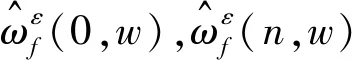
1.2 改进的经验小波变换

构建采样频率为2 000 Hz，数据长度为1 024的仿真信号，其表达式为

y(t)=sin(100πt)+sin(60πt)+cos(40πt)

(8)

对该信号进行傅里叶分解得到频谱图，并根据极大值点进行频带划分，如图1所示。

图1 仿真信号频带划分Fig.1 Simulation signal band division

在仿真信号内加入高斯白噪声，再次进行傅里叶频带划分，如图2所示。

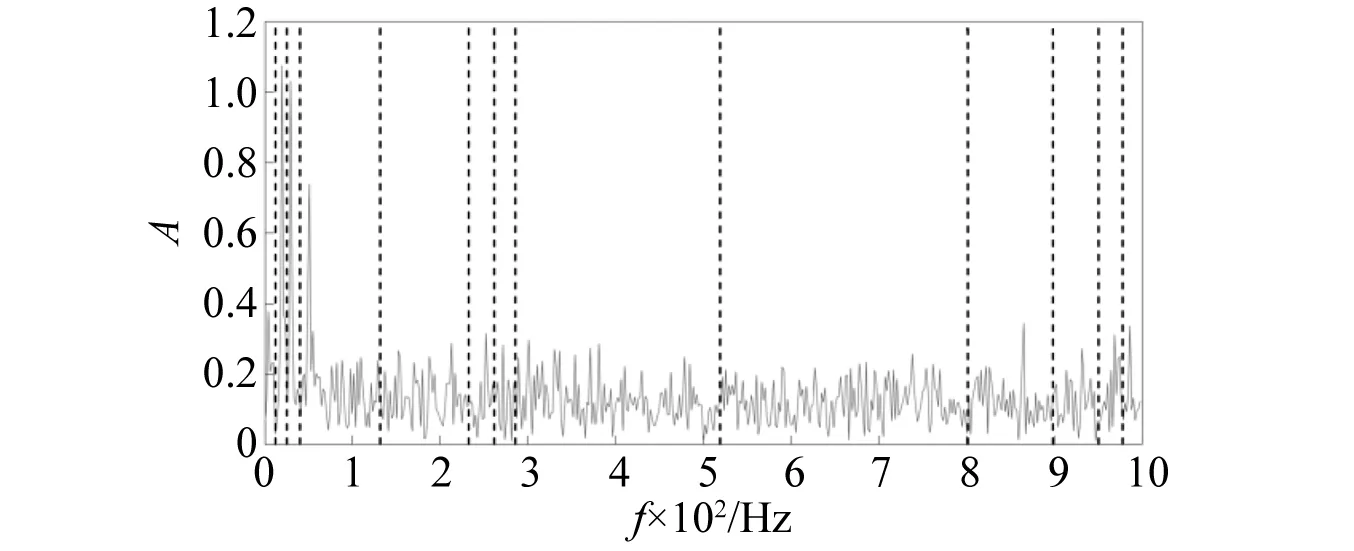
图2 加噪后信号频带划分Fig.2 Signal frequency band division after noise addition

由图可知：噪声的局部极大值点会极大的影响信号频带划分的准确性，降低经验小波变换信号处理的有效性，因此，本文将经验小波变换和相关性阈值去噪方法向结合，减少信号中噪声的影响。

2 基于EWT的信号特征量提取

经验小波变换具有良好的自适应性，而相关性阈值去噪法则具有很强的去噪能力，将两种算法进行融合使用，首先对原始信号进行EWT，将原始信号信息分解到不同的频带内，对不同频带内的分量进行去噪处理，提取与原始信号相关项较大的分量，然后分别利用奇异值分解对频带内的信号进行去噪处理。具体操作方法如下。

步骤1利用相关性阈值去噪法对EWT分量进行去噪处理。

步骤2计算去噪后EWT各个分量与原始振动信号之间的相关系数rj(j=1,2,3,…,N)

式中：f为原始信号；ej为经验小波分量；σf和σej则为原始信号和各分量的标准差；n为各个分量的元素个数。

设置合理的阈值选取与原始信号相关性较大的经验小波分量，既可以去除包含特征信息较少的分量还可以达到降维的目的。通过查阅大量相关文献，在本篇论文中，选取各相关系数的标准偏差作为阈值[12-13]。

步骤3计算步骤1中所选取的EWT分量的能量值

(10)

步骤4根据分量所得到的能量构建原始信号的特征矢量，来表示掘进机截割头所包含的信息。

V=[v1v2…vp]

(11)

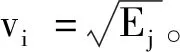
步骤5将改进经验小波变换特征量提取的结果与奇异值分解特征量提取进行比较。

3 奇异值分解

奇异值分解(singular value decomposition,SVD)是一种非线性滤波方式[14-16]，其基本步骤为：①对原始信号进行小波分解并构造时频矩阵；②对重构矩阵进行奇异值分解；③信号还原。

任意一个秩为r的m×n维矩阵A都可以分解为m×m，n×n的两个正交矩阵U和V，可表示为

Am×n=UΣV

(12)

式中，Σ=diag(σ1,σ2,…,σr,0,…,0)为对角矩阵，是矩阵A的奇异值，且满足条件σ1≥σ2≥…≥σr>0。每一个奇异值均代表着原始信号的一个特征[17]。其中，较大的奇异值中包含了原始信号的主要特征，噪声信号以及一些次要特征则被包含在较小的奇异值内。

4 掘进机振动信号特征量提取

4.1 改进经验小波变换特征量提取

利用已经搭建好的掘进机虚拟样机模型，在ADAMS软件中进行仿真，得到掘进机截割头的振动信号，以岩壁硬度为6时z方向上的振动信号为例进行分析，在该信号内添加信噪比为5的高斯白噪声得到信号时域图,如图3所示。

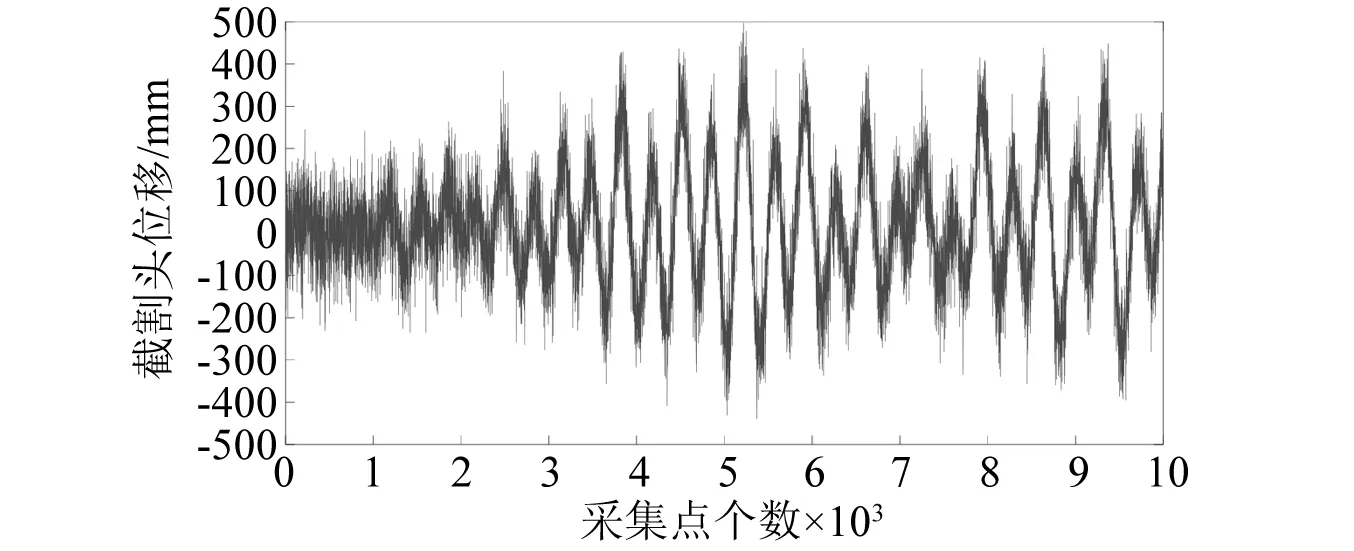
图3 掘进机振动信号变换图Fig.3 Vibration signal transformation diagram of roadheader

对原始信号进行傅里叶分析，得到振动信号的频谱图,如图4所示。

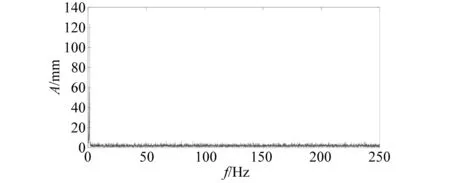
图4 振动信号频谱图Fig.4 Spectrum of vibration signal

根据经验小波变换中提到的频带划分原则，利用频谱图对钻进工况下岩壁硬度分别为6，7，8时的截割头振动信号信号进行频带划分，得到分解后的EWT分量信号，如图5所示。

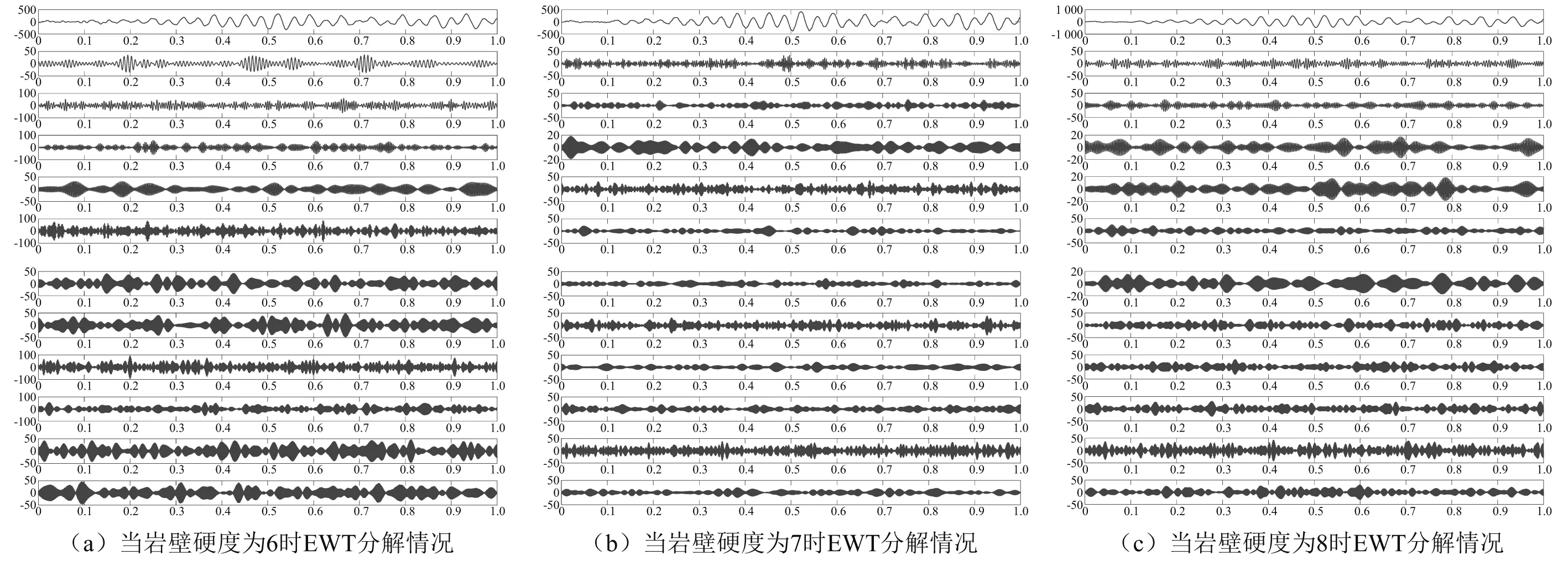
图5 振动信号EWT分量时域图(选取前几个分量为例)Fig.5 Time domain diagram of the EWT component of the vibration signal (take the first few components as an example)

由图5我们可以对不同岩壁硬度下的振动信号分量进行对比，可以发现：不论在频率还是幅值上均有显著不同。这是由于掘进机在切割不同硬度岩壁时，会受到来自岩壁的反向阻力，且岩壁硬度越大，所受到的阻力越大，并随着掘进机切割深度发生规律性变换，最终导致掘进机截割头的振动信号随之发生相应变化。

对各分量于初始信号的相关系数进行求解，其结果如图6(a)所示。此后，利用相关性阈值去噪法对上述分量进行去噪处理，对去噪后的信号进行编号，计算各个分量与原始信号间的相关系数，得到相关性的计算结果，如图6(b)所示。

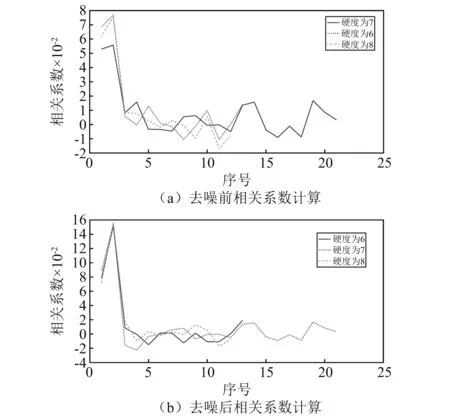
图6 EWT分量相关系数计算Fig.6 EWT component correlation coefficient calculation

由图6可以看出：去噪前后振动信号分量与原始信号的相关性都是先增大后急剧减小，最终逐渐在某个数值附近上下波动，其中，信号的第二个分量与原始信号的相关性最大。这是由于振动信号中始终存在一定的噪声影响，并不能将其完全的剔除。但是，去噪后相关系数的值远大于去噪之前，相关系数过小，信号受噪声影响过大，在进行模式识别时不具有代表性，因此，要对信号进行消噪处理。此外，对比相同硬度下不同分量的相关系数，我们可以看到，相关系数的值越大，说明该分量中所包含的掘进机截割头的振动信号特性越多；而相关系数越小，说明该分量受噪声影响越大，所包含的振动信号特性也相对较少。

本文以各分量与振动信号之间相关系数计算所得到的标准偏差作为阈值对振动信号分量进行删选，不同煤岩硬度下均可以选取前两位与原始信号相关性较大的作为特征矢量。

通过计算有效分量的能量作为掘进机截割头振动信号的特征量，即可得到掘进机截割头振动信号的特征量，如表1所示。

表1 不同岩壁硬度下z方向信号特征量Tab.1 Characteristics of z-direction signal under different rock wall hardness

用同样的方法处理掘进机截割头x，y方向上的振动信号，可以得到这两个方向上的振动信号特征量，分别如表2和表3所示。

表2 不同岩壁硬度下x方向信号特征量Tab.2 Characteristics of x-direction signal under different rock wall hardness

表3 不同岩壁硬度下y方向信号特征量Tab.3 Characteristics of y-direction signal under different rock wall hardness

由表1～表3可以看出:在相同工况下，3个方向上振动信号的特征能量值基本上随着切割岩壁硬度的增大而增大，且第一个分量能量特征值的增幅最为明显，也就是说，第一个分量的能量特征值对掘进机切割岩壁的硬度变化最为敏感。在实际生活中，掘进机切割岩壁硬度越大，其振动信号变化越大，可见，振动信号的特征能量值在某种程度上确实可以反映信号的变化。

在同一岩壁硬度下的，掘进机截割头x,y方向上的第一特征能量值要大于z方向上的特征能量值，但是x,y方向上的第二特征能量值在岩壁硬度发生变化时基本上保持不变，说明当掘进机切割岩壁硬度发生变换时，z方向上的特征能量值对该变化反应最为敏感。

4.2 对比分析

利用奇异值分解方法对掘进机截割头z方向上的振动信号进行特征量提取，一般情况下，振动信号常用分解层数为6,7,8，比较不同分解层数以及不同小波基函数下振动信号所对应的准则值，得到结果如图7所示。

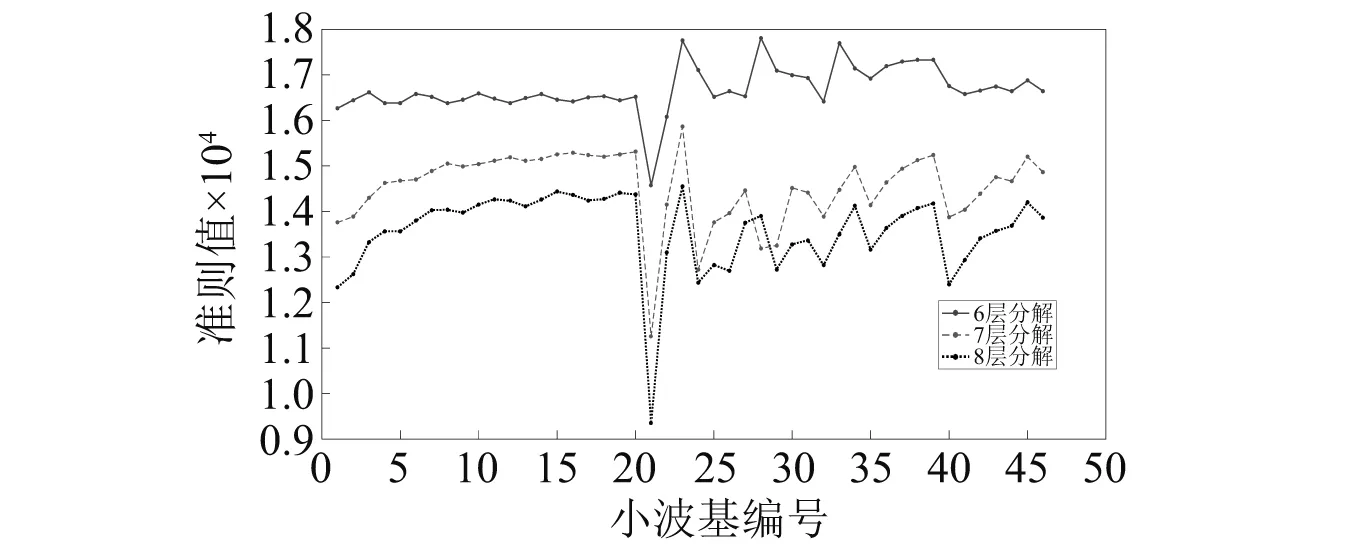
图7 不同情况下振动信号准则值Fig.7 Criterion values of vibration signals in different cases

由图7可知：在同一小波基函数下，当分解层数为6时提取的特征量准则值普遍较大。当分解层数为6，小波基函数为bior3.3时准则值最大，提取的特征量向量最好，因此我们选取6和bior3.3为最优分解层数和最优小波基函数。在该条件下，对振动信号进行特征量提取，得到不同煤岩硬度下z方向上的特征量，如图8所示。

由图8可以看出：虽然利用奇异值分解法对振动信号进行处理的时候也可以对岩壁的硬度进行一个较为简单的区分，但相对于改进的经验小波处理方法来讲，奇异值分解方法处理后的特征量在岩壁硬度发生变换后，硬度较大时的特征量会与较低硬度的特征量存在重叠现象，并不能很好的对掘进机切割岩壁的硬度进行准确的识别。

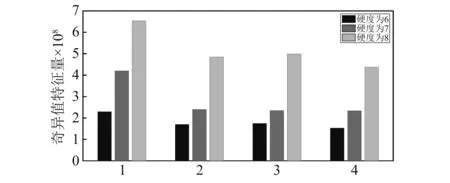
图8 振动信号特征奇异值Fig.8 Singular value of vibration signal characteristics

5 结 论

(1)针对实际情况中掘进机截割头振动信号特征量无法准确提取的问题，提出了基于改进经验小波变换的特征量提取方法，为实现掘进机的动载荷识别提供了方法基础。

(2)将经验小波变换与相关性阈值去噪法相结合，充分利用经验小波变换的自适应性以及相关性阈值去噪的去噪能力，实现了在噪声影响下振动信号特征量较为准确的提取，为实现掘进机的智能化切割岩壁提供了技术基础。

(3)对截割头的振动信号进行处理得到其在不同岩壁硬度下的能量特征值，并将其与奇异值分解方法进行对比，证明前者所得到的特征量对岩壁硬度具有更好的识别性。