结合声学贡献量和拓扑优化的多场点低噪声齿轮箱结构设计方法
2021-09-27王晋鹏
王晋鹏,宋 敏,王 鑫,刘 岚,王 鹏
(1.西安航空学院 机械工程学院,西安 710077;2.中国船舶重工集团第703研究所,哈尔滨 150078;3.西北工业大学 陕西省机电传动与控制工程实验室,西安 710072)
齿轮传动装置作为目前机械设备中最常用的传动形式之一,其在运转过程中产生的空气噪声会对工作人员的健康产生威胁。合理设计齿轮箱结构是降低齿轮传动装置空气噪声的重要手段之一,受到了国内外学者的广泛关注。
声学贡献量分析和结构优化是目前指导低噪声齿轮箱结构设计的两种主要方法。通过声学贡献量可以分析出齿轮箱表面上不同板面或区域对目标场点上声压级的贡献量,对贡献量最大的板面或区域进行改进即可完成低噪声齿轮箱的设计,达到降低目标场点上空气噪声的目标。刘更等[1-3]首先确定了目标场点上声压级峰值对应的频率,再将齿轮箱划分成了多个板面,确定了各板面对声压级峰值的贡献量,最后对贡献量较大的板面进行了改进设计,降低了目标场点上的空气噪声。王晋鹏等[4]确定出了对目标场点上声压级峰值贡献量较大的模态,在这些模态对应的主振型中有明显法向振型的区域添加了肋板,降低了目标场点上的空气噪声。欧健等[5]通过振动响应云图确定了齿轮箱表面振动较大的区域,对该区域进行改进降低了齿轮箱的总辐射声功率级。
将与空气噪声相关的因素作为目标函数和约束条件建立优化模型,根据优化模型的求解结果对齿轮箱结构进行设计即可达到降低空气噪声的目标。目前,以降低空气噪声为目标的优化模型主要包括:结构特征频率设计的优化模型、线弹性结构振动特性设计的优化模型以及声学特性设计的优化模型。在结构特征频率设计优化模型中常用的目标函数包括:基础特征频率最大化[6]、某阶特征频率最大(对空气噪声影响最大的模态对应的特征频率)[7-8]、任意指定阶次的特征频率与给定频率值差的最大化[9]等。在线弹性结构振动特性设计优化模型中常用的目标函数包括:部分区域的稳态幅值响应最小[10-11]、动柔度最小[12]等。在声学特性设计优化模型中常用的目标函数包括:声功率最小[13]、指定场点上的声压最小[14-15]等。在这3种优化模型中,声学特性设计优化模型的计算规模最大,目前主要用于降低简单结构的空气噪声。结构特征频率设计优化模型已经开始用于降低复杂结构的空气噪声,但结构表面局部区域的振动和空气噪声之间的关系需进一步明确。结构特征频率设计优化模型的计算规模最小,是目前复杂结构空气噪声控制中最常用的模型,但增加固有频率和降低空气噪声之间的关系并不直接。
结构优化可以直接确定出肋板的添加位置和形状,但其计算效率明显低于声学贡献量分析。针对这些特点,已有学者将两者结合,将声学贡献量的分析结果作为结构优化模型中的目标函数或约束条件[16],一方面可以使得目标函数与降低空气噪声之间的关系更为直接;另一方面可以提高优化效率。但如何在提高优化效率的同时,达到更理想的降噪效果仍需进一步研究。另外,如何利用结构优化同时降低齿轮箱多个场点上的空气噪声也尚未得到很好解决。
本文以文献[17]中的优化模型为基础,提出了适用于齿轮箱的单场点低噪声拓扑优化模型。根据该优化模型,以多个场点上的平均有效声压级和最大有效声压级为衡量指标,建立了多场点低噪声齿轮箱结构设计方法。运用该方法在单级人字齿轮箱表面新添了肋板。这些肋板的作用是降低齿轮箱空气噪声,称为降噪肋板。根据该方法,可以高效准确确定出齿轮箱表面降噪肋板的布局位置和形状,降低齿轮箱多个场点上的空气噪声,为齿轮箱的结构设计提供指导。
1 单场点低噪声齿轮箱拓扑优化模型
1.1 拓扑优化方程
由于齿轮箱的刚性较好,声压变化只能引起其微小振动,可忽略不计。因此,齿轮箱振动产生的声学响应[18]可表示为
(1)

采用间接边界元法对式(1)求解可得
p(r)=VAT(r)Tvn
(2)
式中:VAT(r)为结构表面各节点对位置r处的声学传递向量;场点位置不同,对应的声学传递向量也不同;vn为结构表面上的法向振动速度向量。
在齿轮箱表面敷设降噪肋板只会引起齿轮箱结构的局部变化,对声学传递向量的影响较小。因此在低噪声齿轮箱的拓扑优化设计中可认为声学传递向量不变。此时,齿轮箱的空气噪声只与法向振动速度有关,法向振动速度(即法向振型)越明显,齿轮箱的空气噪声就越大。只要能够减小齿轮箱表面的法向振动速度就可降低其空气噪声。
齿轮箱表面不同区域上振动速度产生的声压也不同,即各区域对目标场点上空气噪声的贡献量并不相同。声学贡献量越大,表明在目标场点上的总声压中,由该区域振动产生的声压所占比例越大。降低该区域上法向振动速度产生的降噪效果越明显。因此为了能在取得较好降噪效果的同时提升计算效率,本文中只降低声学贡献量最大区域上的法向振动速度。声学贡献量最大区域的位置可通过以下步骤确定[19]。
首先,计算出齿轮箱表面各节点对目标场点上声压级的声学传递向量,确定出声学传递向量幅值均在最大幅值0.8倍以上的区域,这些区域上具有较大的声学传递向量。其次,计算出齿轮箱各阶模态对目标场点上声压级的贡献量,分析贡献量较大模态对应的法向主振型,确定出各阶主振型中模态位移的最大值及模态位移数值均在最大值0.8倍以上的区域,这些区域上具有较大的法向振动速度。最后,在同时具有较大声学传递向量和法向振动速度的区域上划分板面并进行板面声学贡献量分析,贡献量最大的板面即为对目标场点上声压级贡献量最大的区域。
通过减小该区域上的法向振动速度建立了如下拓扑优化方程
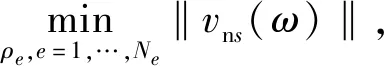
(3)

1.2 灵敏度分析
齿轮箱的速度响应通常采用模态叠加法计算。取齿轮箱的全部阶模态进行计算可获得最为准确的结果,但计算时间会非常长。研究表明,当固有频率远大于激励频率时,这些固有频率对应的模态对速度响应的影响非常小。
对于齿轮箱,激励载荷(即轴承动载荷)的较大值通常出现在齿轮系统的啮合频率及其倍频处。假设啮合频率i倍频及其以后所有频率处,各轴承上动载荷的幅值均小于动载荷峰值的1/100,表明该频率及其以后所有频率处的激励均非常小,可以忽略;则固有频率大于该频率所对应的模态对齿轮箱速度响应的影响会非常小。因此为了提升计算效率,通常只取齿轮箱的前l阶模态(第l阶模态对应的固有频率大于啮合频率的i倍频)计算其速度响应。此时齿轮箱的速度响应可表示为
(4)
式中:j为复数单位,j2=-1;ω为角频率;φi为齿轮箱的第i阶特征向量;ωni为齿轮箱的第i阶固有频率;ξi为齿轮箱的i阶模态阻尼比。
式(4)中φi和Di均与齿轮箱的单元体积密度(即拓扑优化模型中的设计变量)有关,因此齿轮箱速度响应对设计变量的灵敏度为
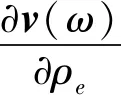
(5)
式(5)中第i阶特征向量φi对单元体积密度的灵敏度满足
(6)
(7)
第i阶固有频率ωni对设计变量的灵敏度可表示为
(8)
假设α为一列向量,其值为
α={0,0,…,0,1,0,…,0}T
(9)
向量α中元素1的位置与齿轮箱速度响应列向量中第s个节点上法向振动速度对应的位置相同。此时,齿轮箱第s个节点上法向振动速度可表示为
vns(ω)=αTv(ω)
(10)
将齿轮箱第s个节点上法向振动速度对设计变量求导可得
(11)
齿轮箱第s个节点上法向振动速度的幅值为
(12)
式中:Re为复数的实部;Im为复数的虚部。
该幅值对设计变量的灵敏度为

(13)
2 多场点低噪声齿轮箱结构设计流程
齿轮箱会在多个方向的场点上产生空气噪声,单个场点上的声压级并不能全面反映齿轮箱的空气噪声水平。假设第i个场点上的有效声压级为Lepi,则多个场点上的平均有效声压级和最大有效声压级可表示为
(14)
Lmaxep=max{Lep1,Lep2,…,Lepnf}
(15)
式中:Leep为多个场点上的平均有效声压级;Lmaxep为多个场点上的最大有效声压级;nf为场点总数。
平均有效声压级和最大有效声压级可以反映多个场点上空气噪声的平均水平和最大水平,从而较为全面地反映齿轮箱的空气噪声水平。因此以这两个参数为衡量指标提出了可同时降低多个场点上空气噪声的齿轮箱结构设计流程,如图1所示。具体步骤如下:
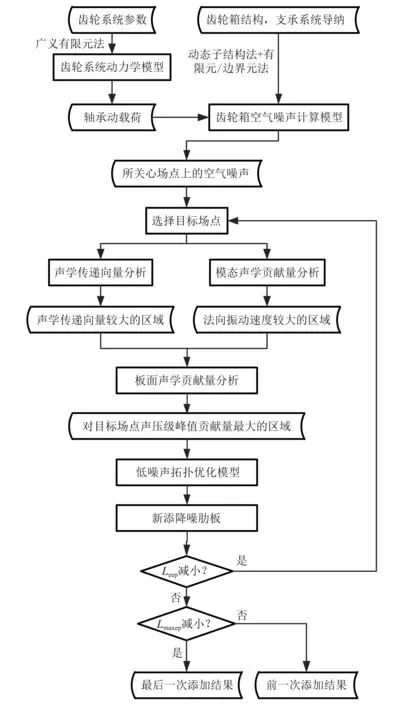
图1 低噪声齿轮箱结构设计流程Fig.1 The design procedure of gearbox with low noise
步骤1根据齿轮系统参数,齿轮箱结构,支撑系统导纳采用有限元/边界元法计算齿轮箱的空气噪声[20]。在所有关心场点中,选择有效声压级最大的场点为目标场点。通过频谱分析,确定出目标场点上声压级峰值对应的频率。
步骤2计算并分析声学传递向量,模态声学贡献量和板面声学贡献量,确定出对目标场点上声压级峰值贡献量最大的区域。建立式(3)所示的拓扑优化模型对齿轮箱进行拓扑优化,并根据拓扑优化结果在齿轮箱表面新添降噪肋板。
步骤3对比新添降噪肋板前后目标场点上的空气噪声,判断新添降噪肋板后所有关心场点上的Leep是否减小。如果减小,表明齿轮箱仍有改进设计的空间,重新选择有效声压级最大的场点为目标场点对齿轮箱进行拓扑优化并新添降噪肋板。如果没有减小,表明齿轮箱已无改进设计的空间。此时需要判断最后一次新添降噪肋板后所有关心上的Lmaxep是否减小。如果减小,表明最后一次降噪肋板的添加有效,选择最后一次添加结果为最终结果,如果没有减小,表明最后一次添加无效,选择前一次添加结果为最终结果。
3 多场点低噪声齿轮箱结构设计结果
3.1 齿轮传动装置模型
单级人字齿轮系统的实体模型,如图2(a)所示。齿轮箱的实体模型,如图2(b)和图2(c)所示。齿轮传动装置通过14个螺栓安装在支承系统上,连接点的编号,如图2(c)所示。各连接点处,支承系统自加速度导纳的半对数幅频图,如图3所示。

图2 人字齿轮传动装置实体模型Fig.2 The model of double-helical gear transmission system
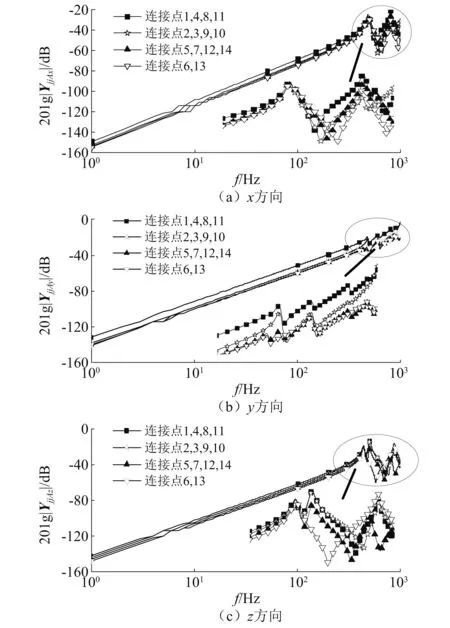
图3 各连接点处支承系统自导纳的半对数幅频图Fig.3 Amplitude-frequency curves of the supporting system’s self acceleration admittance on each connection point
由图3可知:在低频段,各连接点处支承系统自导纳的半对数幅频图均为刚度线(斜率为40 dB/decade的直线);随着频率的增加,依次出现共振和反共振。以上特性与无阻尼约束二自由度系统自导纳半对数幅频图的特性相同。因此空气噪声计算中,在每个连接点处的x,y,z方向上都将支承系统等效为了无阻尼约束二自由度系统。
3.2 轴承动载荷
采用广义有限元法[21]建立了图2中人字齿轮系统的有限单元模型,如图4所示。图4中:输入(输出)功率点位于输入(输出)端平键的中点处,轴承节点位于轴承中点处,齿轮节点位于齿宽中点处,轴节点位于轴端、轴截面尺寸突变处,轴承端点处及齿轮端点处。轴单元建立在同一根轴上的节点之间,文中用Timoshenko梁单元模拟轴单元。轴承单元建立在轴承节点和固定点之间,文中用4个油膜刚度系数和4个油膜阻尼系数模拟滑动轴承。啮合单元建立在相互啮合的齿轮节点之间,文中用两个螺旋线方向相反的斜齿轮啮合单元等效人字齿轮啮合单元。
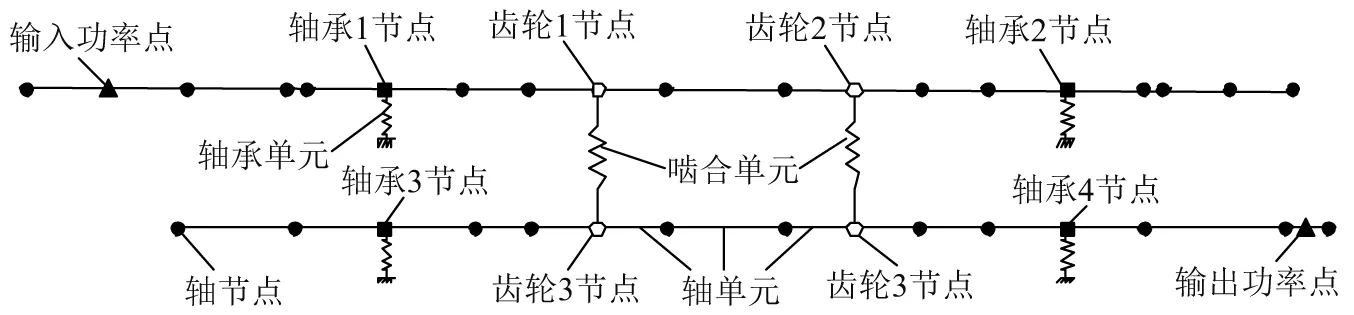
图4 人字齿轮系统的有限单元模型Fig.4 The finite element model of double helical gear system
求解人字齿轮系统的有限单元模型获得了各轴承节点处的位移和速度,根据式(16)计算获得了各轴承处的动载荷。当输入转速入转速为4 000 r/min,输出扭矩为15 000 N·m时,各轴承上的动载荷频谱如图5所示。由图5可知:各轴承上动载荷的幅值均出现在啮合频率处(2 466.67 Hz)。
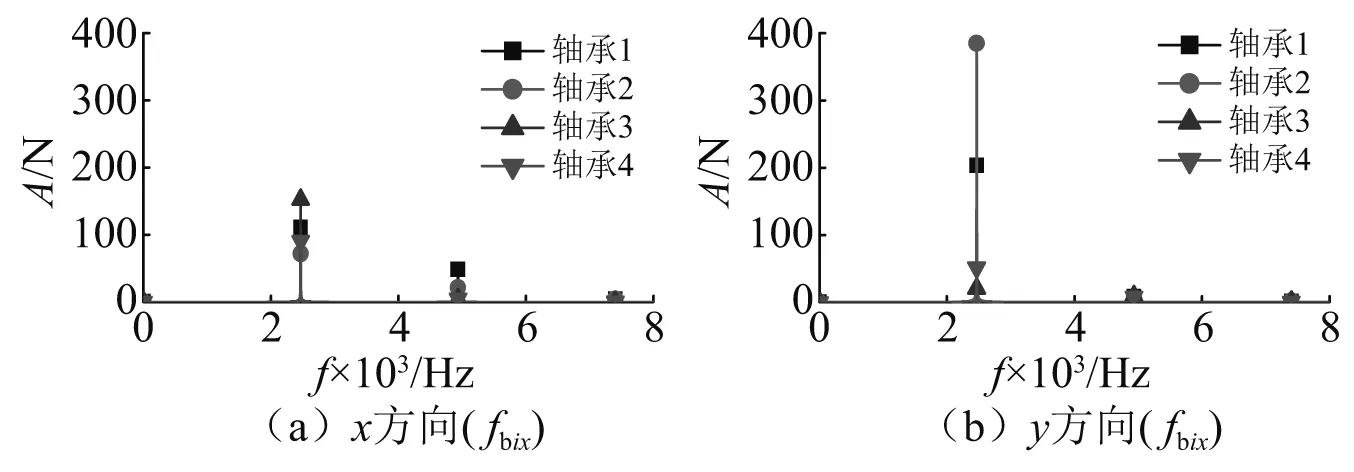
图5 轴承动载荷频谱Fig.5 The bearing dynamic loads in frequency domain
(16)
3.3 空气噪声分析
运用动态子结构法对支承系统进行了等效,以图5中的轴承动载荷为激励,采用有限元/边界元法计算获得了齿轮箱的空气噪声。由图2可知:齿轮箱的基本形状为方形。针对该齿轮箱的结构特点,空气噪声计算中建立了方形声场,如图6所示。声场的前侧(输入侧)、后侧(输出侧)、左侧、右侧及上侧与齿轮箱表面间的距离均为1 m;声场下侧为地面的位置,与齿轮箱下表面间的距离等于支承系统的高度。齿轮箱前表面、后表面、左表面、右表面及上表面的振动均会向外辐射噪声;由于支承系统和地面的作用,下表面空气噪声的辐射会受到限制,同时下方的空气噪声也很难测量。因此选择声场前侧、后侧、左侧、右侧及上侧中心处的场点为所关心场点,如图6所示。
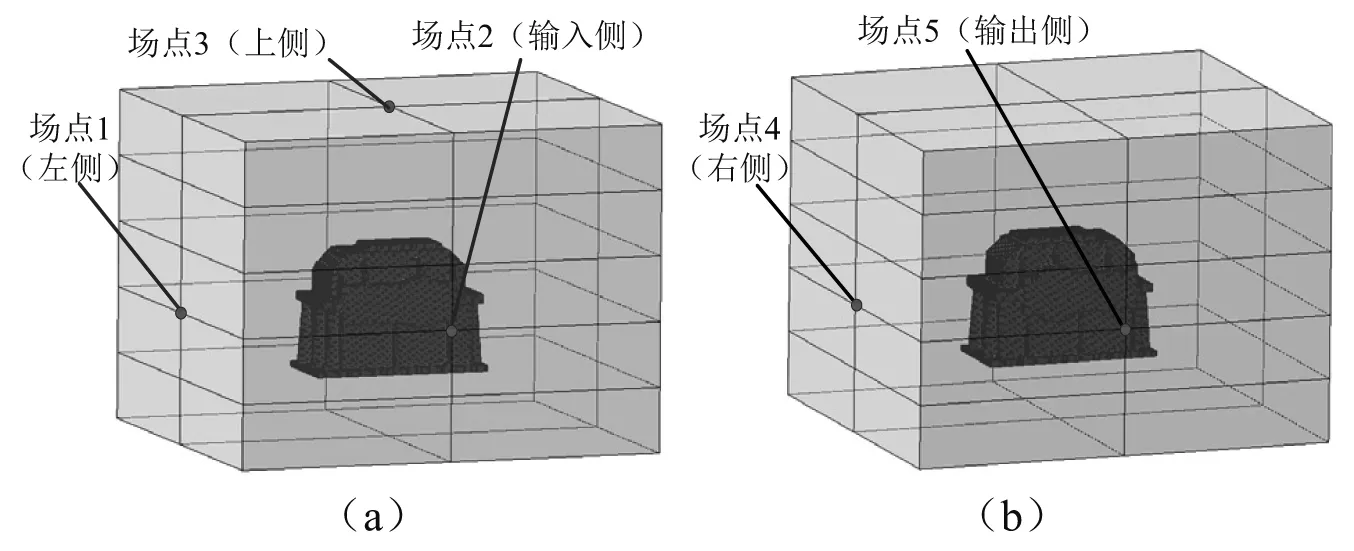
图6 各场点位置Fig.6 The position of each field point
当输入转速为4 000 r/min,输出扭矩为15 000 N·m时齿轮箱在所关心场点处的有效声压级,如表1所示。

表1 齿轮箱各场点上的有效声压级Tab.1 The equivalent sound pressure level of gearbox at each field point dB(A)
3.4 多场点低噪声齿轮箱结构设计过程
由表1可知:场点2上的有效声压级最大,因此首先选择该场点为目标场点。通过频谱分析可知,啮合频率处的声压级最大。声学传递向量的计算结果表明啮合频率处齿轮箱输入侧表面上的声学传递向量较大,而其余表面上的声学传递向量均较小。主要因为场点2的位置正对于齿轮箱输入侧表面。模态声学贡献量的分析结果表明,齿轮箱第208阶、第210阶和第211阶模态对场点2上声压级峰值的贡献量最大。这3阶模态对应的法向主振型,如图7所示。由图7可知:输入侧表面上的区域1、区域2、区域3和区域4上具有较大的模态位移,表明这4个区域上同时具有较大的法向振动速度。在这4个区域上划分了板面并分析了各板面的声学贡献量,结果表明区域1上的声学贡献量最大,达到了15.5%。
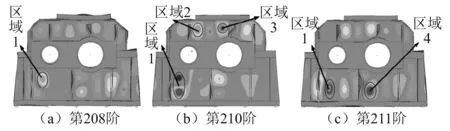
图7 齿轮箱的第208阶、210阶和211阶法向主振型Fig.7 The 208th,210th and 211th normal mode shape of gearbox
以减小区域1上的法向振动速度建立了拓扑优化模型并对齿轮箱进行了拓扑优化。优化模型中ηv取值为0.5。为了提升优化效率,只选取了齿轮箱输入侧表面上包含区域1的部分表面作为了设计区域。齿轮箱的第一次拓扑优化结果,如图8(a)所示。根据该结果在齿轮箱表面新添了降噪肋板,如图8(b)所示。

图8 齿轮箱的第一次改进设计Fig.8 The improved design of gearbox for the first time
第一次新添降噪肋板前后场点2上的声压级频谱,如图9所示。由图9可知:添加降噪肋板后场点2上的声压级峰值降低了13.56 dB(A),表明建立的单场点低噪声齿轮箱拓扑优化模型有效。

图9 第一次添加降噪肋板前后场点2上的声压级频谱Fig.9 The sound pressure level spectrum at field point 2 before and after adding nose reduction rib for the first time
第一次添加降噪肋板前后5个关心场点上的空气噪声对比,如表2所示。由表2可知:第一次添加降噪肋板后,场点2上的有效声压级降低了13.49 dB(A)。5个场点上的平均有效声压级由65.08 dB(A)降至62.52 dB(A),降低了2.68 dB(A),表明第一次降噪肋板的添加有效。
由表2可知:第一次新添降噪肋板后,场点5上的有效声压级最大,因此选择该场点为目标场点对齿轮箱再次进行了拓扑优化。根据声学传递向量和模态声学贡献量的分析结果,确定出了6个同时具有较大声学传递向量和法向振动速度的区域,如图10所示。由于场点5正对于齿轮箱的输出侧表面,因此这6个区域均位于齿轮箱输出侧表面。在这6个区域上划分了板面并分析了各板面的声学贡献量,结果表明区域1上的声学贡献量最大,达到了55.9%。

表2 第一次添加肋板前后5个场点上的有效声压级Tab.2 The equivalent sound pressure level at five field points before and after adding new ribs for the first time dB(A)

图10 同时具有较大声学传递向量和法向振动速度的区域Fig.10 The regions with large acoustic transfer vector and normal vibration velocity
以降低区域1上的法向振动速度建立了拓扑优化模型并齿轮箱进行了拓扑优化,优化结果如图11(a)所示。优化模型中,ηv取值为0.5,优化区域只选择了输出侧表面上包含区域1的部分表面。根据优化结果在齿轮箱的输出侧表面新添了降噪肋板,如图11(b)所示。
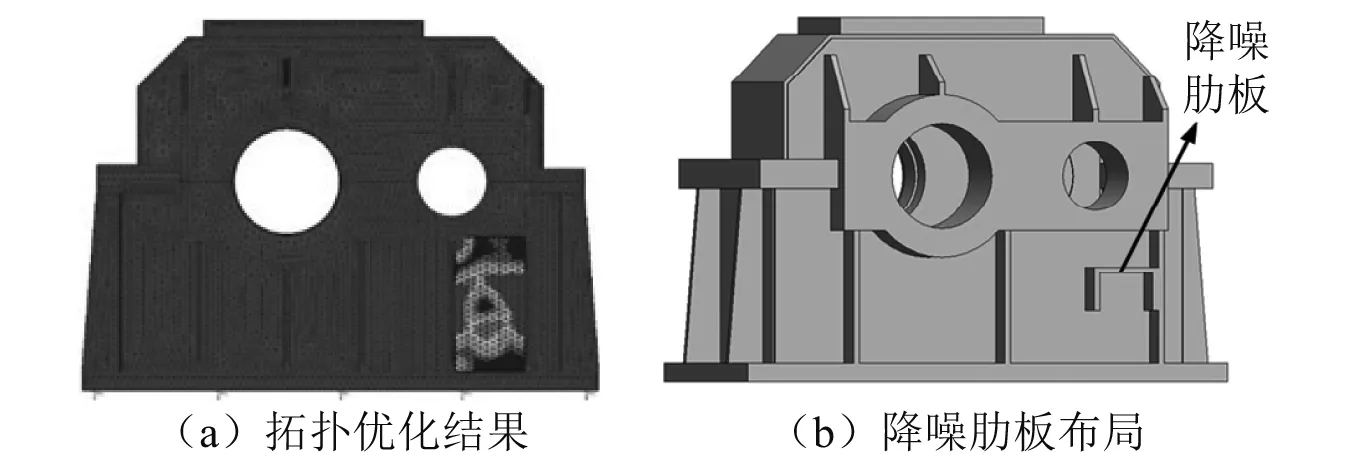
图11 齿轮箱的第二次改进设计Fig.11 The improved design of gearbox for the second time
计算了第二次新添降噪肋板后齿轮箱的空气噪声,并与新添降噪肋板前(第一次新添肋板后)齿轮箱的空气噪声进行了对比,结果如表3所示。由表3可知:第二次新添降噪肋板后,场点5上的有效声压级降低了7.23 dB(A)。5个场点上的平均有效声压级由62.52 dB(A)降至60.39 dB(A),降低了1.13 dB(A),表明第二次降噪肋板的添加有效。
由表3可知:第二次新添降噪肋板后,场点1上的有效声压级最大。因此选择该场点为目标场点对齿轮箱进行了第三拓扑优化,结果如图12(a)所示。根据优化结果在齿轮箱左侧表面上新添了降噪肋板,如图12(b)所示。第三次新添降噪肋板前后各场点上的有效声压级以及对应的平均有效声压级,如表4所示。由表4可知:第三次新添降噪肋板后场点1上的有效声压级降低了0.88 dB(A)。5个场点上的平均有效声压级由60.39 dB(A)降至59.56 dB(A),降低了0.83 dB(A),表明降噪肋板的第三次添加有效。

表3 第二次添加肋板前后5个场点上的有效声压级Tab.3 The equivalent sound pressure level at five field points before and after adding new ribs for the second time dB(A)

图12 齿轮箱的第三次改进设计Fig.12 The improved design of gearbox for the third time

表4 第三次添加肋板前后5个场点上的有效声压级Tab.4 The equivalent sound pressure level at five field points before and after adding new ribs for the third time dB(A)
第三次添加降噪肋板后场点5上的有效声压级最大,因此重新选择该场点为目标场点对齿轮箱进行了拓扑优化,结果如13(a)所示。根据优化结果在齿轮箱表面新添了降噪肋板,如图13(b)所示。
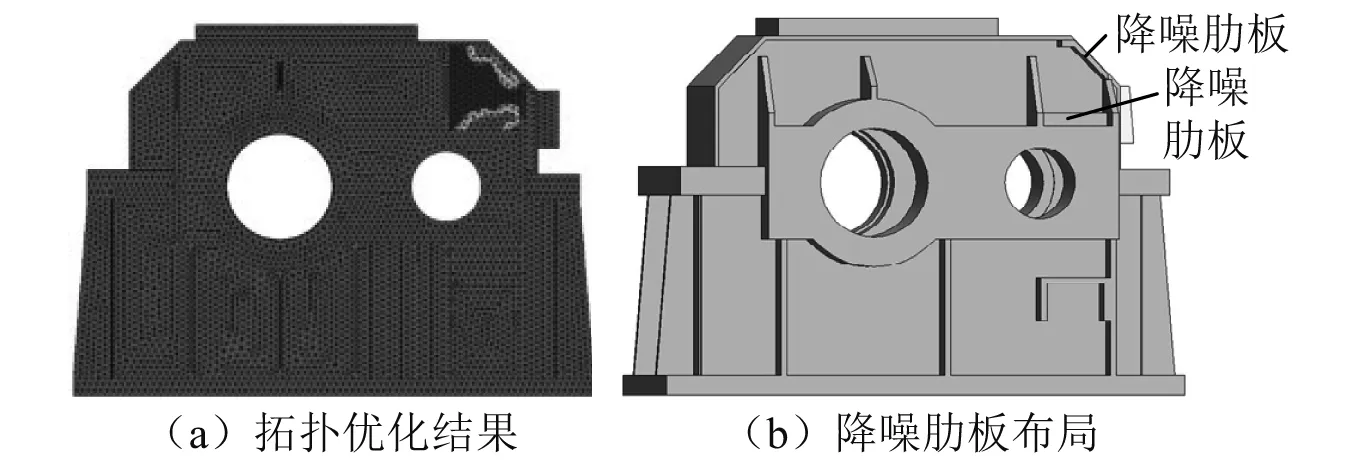
图13 齿轮箱的第四次改进设计Fig.13 The improved design of gearbox for the third four time
第四次新添降噪肋板前后齿轮箱的空气噪声对比,如表5所示。由表5可知:第四次添加降噪肋板后场点5上的有效声压级降低了6.64 dB(A)。但5个场点上的平均有效声压级却从59.56 dB(A)增加至60.10 dB(A),表明齿轮箱已无改进空间,降噪肋板的添加结束。第四次添加降噪肋板后虽然平均有效声压级有所增加,但5个场点上的最大有效声压级减小了4.34 dB(A),表明第四次降噪肋板的添加有效。

表5 第四次添加肋板前后5个场点上的有效声压级Tab.5 The equivalent sound pressure level at five field pointsbefore and after adding new ribs for the fourth time dB(A)
经过四次添加后,最终的降噪肋板布局,如图14所示。由图14可知:为了降低齿轮箱的空气噪声,分别在其输入侧、输出侧和左侧新添了降噪肋板。

图14 多场点低噪声齿轮箱结构设计结果Fig.14 The design result of gearbox with low noise at multi field points
4 齿轮箱结构设计前后空气噪声对比
添加降噪肋板前后齿轮箱在各关心场点上的空气噪声对比,如表6所示。降噪肋板布置在了齿轮箱的左侧、输入侧和输出侧,因此添加降噪肋板后场点1、场点2和场点5上的空气噪声有了明显降低。由表6可知:添加降噪肋板后5个场点上的最大有效声压级减小了9.44 dB(A)。5个场点上的平均有效声压级由65.08 dB(A)降至60.10 dB(A)降低了4.98 dB(A)。表明建立的多场点低噪声齿轮箱结构设计方法有效。
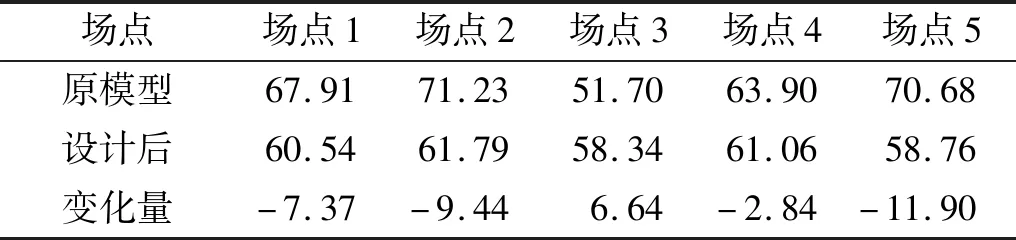
表6 改进设计前后齿轮箱各场点上的有效声压级Tab.6 The equivalent sound pressure level of gearbox at each field point before and after improvement dB(A)
添加降噪肋板前后齿轮箱声场上的声压级分布云图,如图15和图16所示。由图15和图16可知:添加降噪肋板后不仅5个场点上的空气噪声有所降低,整个声场上的空气噪声均有所降低。
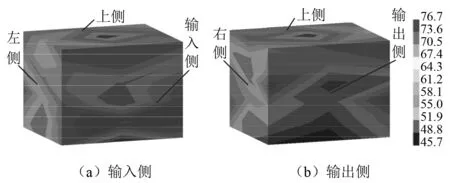
图15 改进设计前齿轮箱声场上的声压级分布云图Fig.15 The sound pressure level distribution at sound field of gearbox before improvement
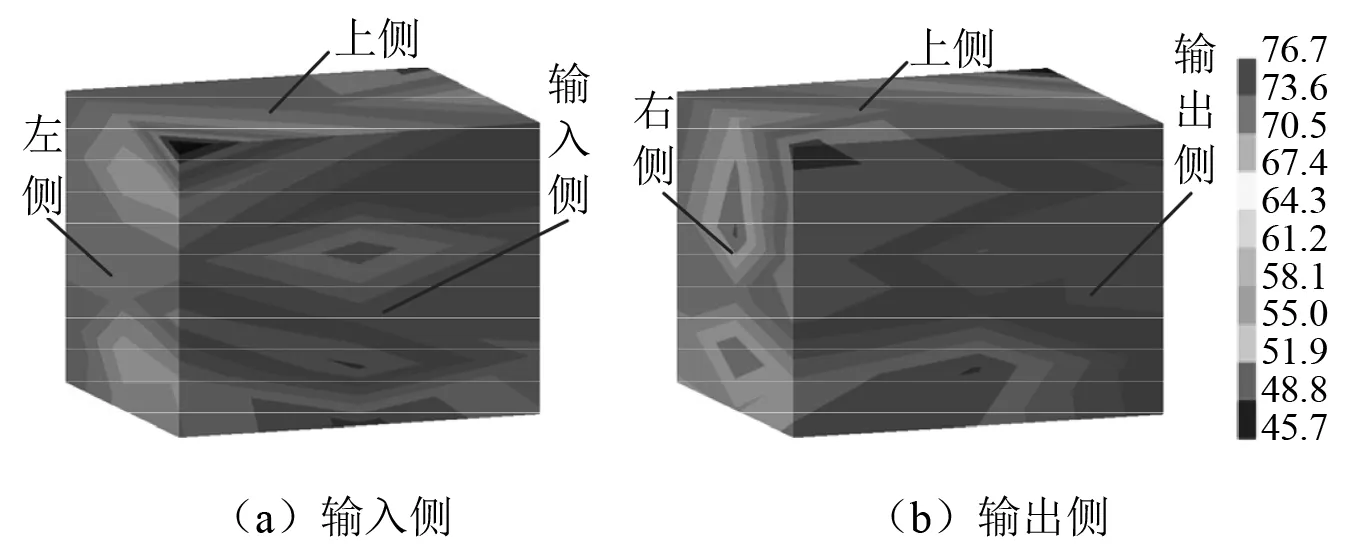
图16 改进设计后齿轮箱声场上的声压级分布云图Fig.16 The sound pressure level distribution at sound field of gearbox after improvement
5 结 论
(1)以降低声学贡献量最大区域上法向振动速度为目标和约束条件构建的拓扑优化模型可指导齿轮箱表面降噪肋板的添加,从而有效减小目标场点上的空气噪声。
(2)在齿轮箱的拓扑优化过程中,只取齿轮箱上包含声学贡献量最大区域的部分表面为设计区域不仅可以取得较好的降噪效果,还可以有效提升优化效率。
(3)建立的多场点低噪声齿轮箱结构设计方法不仅可以有效降低多个场点上的平均有效声压级和最大有效声压级,还可以降低整个齿轮箱声场上的空气噪声。
(4)降噪肋板的主要作用是降低齿轮箱的空气噪声,与齿轮箱表面的常肋板相比其结构形式更加多样。
