锂离子动力电池风道模型设计与散热仿真
2021-09-27董小平张锦涛张昭卿
董小平,张锦涛,李 健,张昭卿
(1.河北大学质量技术监督学院,河北 保定 071002;2.保定市新能源车辆动力工程技术研究中心,河北 保定 071002;3.河北省新能源汽车动力系统轻量化技术创新中心(筹),河北 保定 071002)
1 引言
电动汽车的能量提供在于动力电池,其性能的好坏直接影响电动汽车的运行。在汽车行驶过程中,电池放电时产生的热量散失快慢以及不同位置的温差势必影响电池性能,尤其是电池的使用寿命。在众多车用动力电池中,锂离子电池应用尤为广泛。目前,锂离子动力电池主要以风冷、液冷和相变冷却等方式散热,相比之下,后二者散热效果较好,但结构复杂、成本高;风冷虽然散热效果低,但其散热结构简单、成本低。因此,风冷已广泛用于动力电池模组的散热[1-3]。如马强等采用串行出风口与并行进风口后,电池包温度分布均匀性提高,同时还发现,放电倍率影响电池的发热和不同位置的温差,倍率较高时,其不同位置的发热量和温差均较大[4]。另外,对模拟电池增加辅助散热孔后电池的最高温度可降低6.3 ℃,增加气体引流板后可将电池模组最大温差缩小到5.9 ℃。王明强等发现,在-20 ℃下加热时,短时间内三元软包装锂离子电池温度几乎不变,但25 min后电池不同位置出现温差,最大温差值为7.9 ℃;在40 ℃下,1.5 C快充工况下,电池温度不超过48 ℃,最大温差为3.9 ℃[5]。姚程宁等报道,当热功率密度为0.365 8 W·cm-2时,强制风冷散热条件下,采用微通道热管阵列技术可维持热源处表面温度在45 ℃以下,温差低于1.3 ℃,低于无微通道热管阵列导热情况下的温差(3.8 ℃),与烧结热管组的温度相比,微通道热管阵列组的最大温度可降低15.1 ℃,表面温差降低14 ℃,这说明微通道热管阵列技术具有显著降温和均温等优势[6]。基于以上,本文以5×10等间距排列的18650锂离子电池模组为研究对象,对锂离子动力电池风道模型进行了设计,并进行不同条件下的散热仿真。
2 模型与仿真
2.1 锂离子动力电池生热机理
为了分析电池的产热状况,首先对电池进行简化条件假设:(1)电池同一部分的组成物质、密度与比热容相同且恒定;(2)电池在各个方向上的导热系数恒定;(3)电池产热均匀且不变;(4)电池的初始温度与环境温度保持一致;(5)电池辐射传热和对流传热不考虑。
基于假设(1)、(2)和(5),形成电池热耦合模型公式[7-9],如等式(1):
(1)
(2)
式(1)中,ρ为电池密度;Cp为比热容;T为电池热力学温度;t为时间;λr、λφ、λz分别为柱坐标三个方向上的导热系数;q为单位体积电池生热速率,其计算公式如等式(2)。式(2)中,q为生热速率;I为电流强度;V为电池体积;EOC为电池开路电压;U为电池工作电压;T为电池热力学温度;dEOC/dT为温熵系数,常取0.3 mV·K-1。
本论文以18650锂离子电池(LG、MJ1、3.5 Ah)为研究对象,直径为18 mm,高为65 mm。该电池与空气的热物理参数如表1所示。
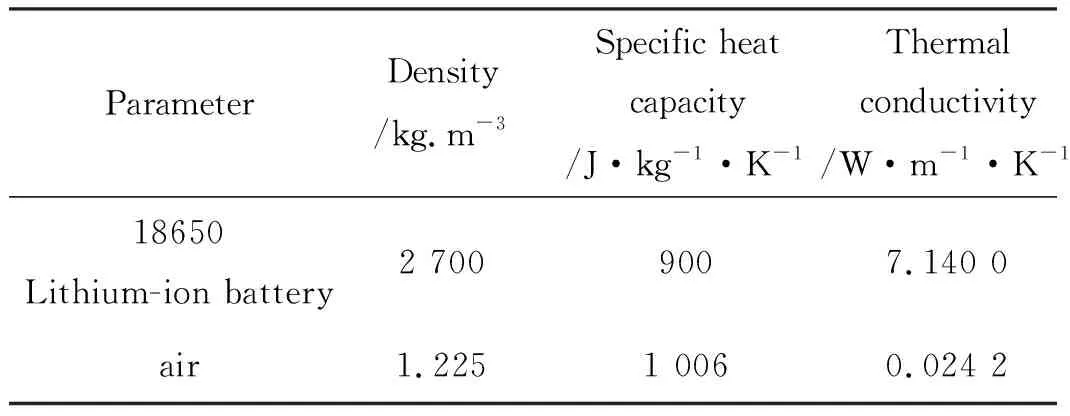
表1 热物理参数表[7]Table 1 Thermophysical parameter table[7].
2.2 风道模型建立
为了研究电池的散热性能,对风道方向进行横向和纵向风道设置,分别如图1(a)和图1(b)。在图1(a)中,采用5×10排列,进风口为楔形式,与水平夹角为10°,风道出风口尺寸为25×228 mm2,进出风口与箱体外壁之间的间距均为5 mm;电池之间的间距为4 mm,中心距为22 mm,电池组与出入风口侧壁面的间距为9 mm,与两侧壁面的间距为6 mm,电池顶部与箱体的间距为10 mm。纵向风道除了出风口位置和出风口尺寸(25×118 mm2)进行了改动外,其余参数与横向风道模型一致。在横向风道模型的基础上,电池排布的俯视图采用长方形、错位、梯形和双梯形等排布(如图2);它们对应的出风口尺寸分别为:25×272 mm2、25×272 mm2、25×237 mm2和25×272 mm2。
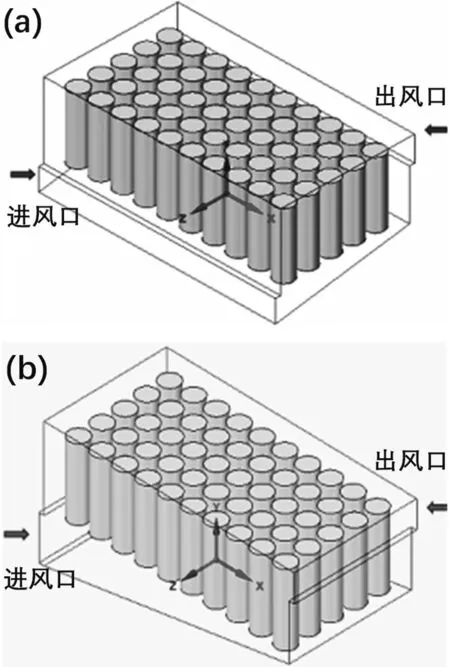
图1 电池包模型(a)横向风道模型,(b)纵向风道模型Fig.1 Battery pack model (a)transverse duct model,(b)longitudinal duct model.

图2 电池排布俯视图(a)长方形,(b)错位,(c)梯形(d)双梯形Fig.2 Top view of battery arrangement (a) rectangular,(b) dislocation,(c) ladder,(d) double trapezoid.
为了进一步提高风道的散热能力,基于横向风道模型,提出两种方案进行优化。方案1:在其进风口侧壁上方增加一个出风口,其尺寸为25×228 mm2,如图3(a);方案2:基于方案1,在模型两侧壁面上分别开设4个散热孔,每个孔的面积为5×50 mm2,孔与孔的间距为10 mm,孔上端距离电池包顶端为15 mm,与出风口侧相距最近的散热孔与该侧壁的距离为47 mm,如图3(b)。
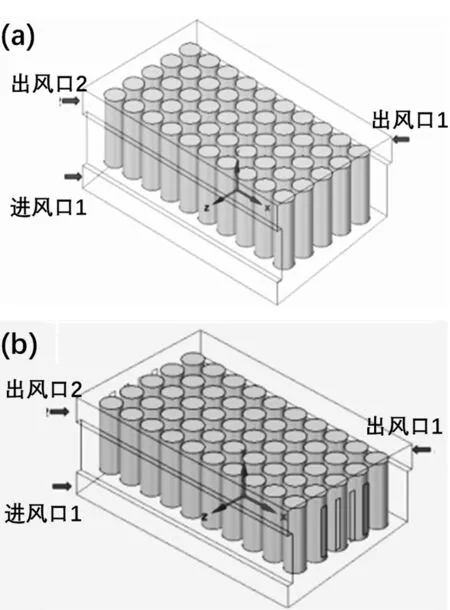
图3 电池包模型(a)方案1,(b)方案2Fig.3 Battery pack model (a)scheme 1,(b)scheme 2.
2.3 网格划分
首先进行流体设置与边界设置。在ANSYS AIM软件中,选用流体固体热传递进行仿真。模型的进风口空气温度设置为25 ℃,即为环境温度,风速分别为1 m·s-1、2 m·s-1、3 m·s-1、4 m·s-1和5 m·s-1,风的强度和黏度比适中;同时,出口的静压为0,壁面与空气的对流交换热系数设置为15 W·m-2·C-1。
其次进行网格划分与求解设置。选用ANSYS AIM软件中流体固体热传递形式划分网格,网格划分的单元形状为四面体,保留中间节点,边界层平滑过渡,单元数量为561 186,节点数量为164 951,结合流体设置与边界设置进行求解,残差设置为容差1×10-5。网格划分如图4。

图4 网格划分Fig.4 Mesh division.
3 结果与分析
3.1 风道方向与电池排布对电池模组散热的影响
为了对比横纵风道模型对电池散热的影响,在设置风速下采用1 C进行放电。横纵向风道模型中俯视图以长方形排列的电池随风速的温度变化如图5。由图5可知,在本文研究的范围内,随着风速增加,电池的最高温度、最低温度、平均温度以及温差均降低,即当风速从1 m·s-1增加到5 m·s-1时,横向风道模型的电池最高/最低/平均温度/温差分别从37.73 ℃、30.07 ℃、33.55 ℃和7.66 ℃降低到31.36 ℃、26.31 ℃、28.20 ℃和5.05 ℃;纵向风道模型的电池最高/最低/平均温度分别从39.17 ℃、29.17 ℃、34.08 ℃和9.99 ℃降低到32.95 ℃、26.28 ℃、28.56 ℃和5.66 ℃。对比横纵向风道模型的电池温差,发现在测试的相同风速下,横向风道模型的电池的最高温度的温差低于纵向风道模型的电池温差,这说明横向风道模型散热性能优于纵向风道模型。因此,在横向风道模型基础上,研究电池排列方式对电池温度的影响。在不同排列方式下,电池温度随风速的变化图如图6。在四种电池排列方式下,随着风速增加,电池的最高温度、平均温度和温度差均降低。相比之下,在不同风速下梯形方式排布时的电池最高温度、最低温度、平均温度相对较小,错开排布时的电池最高温度相对较高;长方形排布时的电池最低温度与平均温度相对较高。另外,不同排列方式的电池温度差(见图6(d))与风速有关,当风速为1 m·s-1时,电池温度差由大到小的顺序为:错开排列、梯形排列、长方形排列、双梯形排列。但风速大于1 m·s-1时,电池的温差由大到小的排列顺序为:错开排列、长方形排列、双梯形排列、梯形排列。
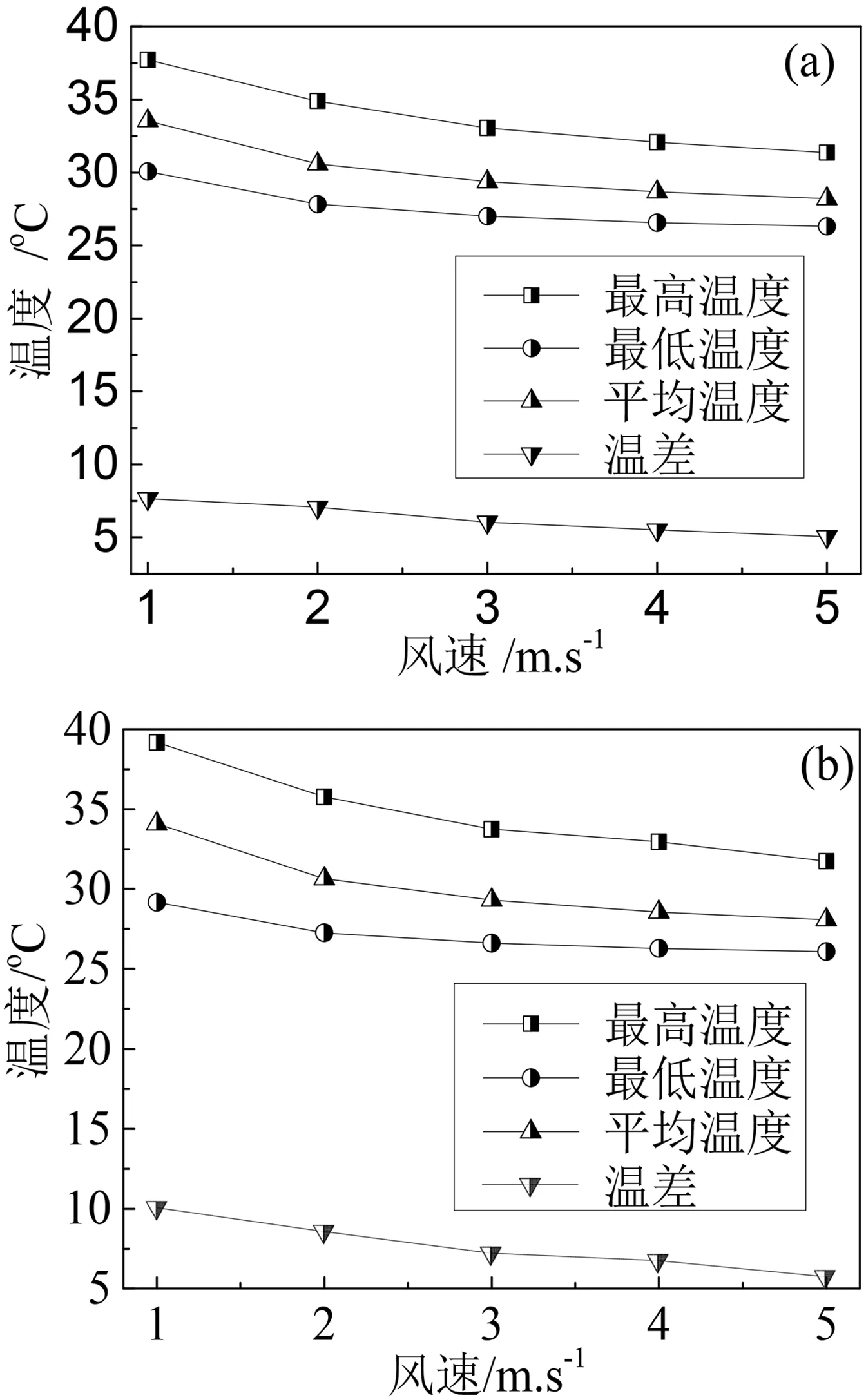
图5 电池温度对风速的变化(a)横向,(b)纵向Fig.5 Changes of battery temperature to wind speed (a) horizontal,(b) vertical.
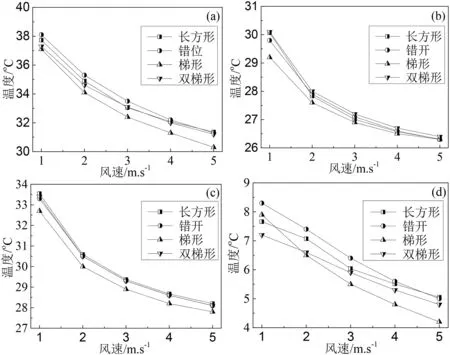
图6 不同排列方式下电池温度和温差随风速的变化(a)最高温度,(b)最低温度,(c)平均温度,(d)温度差Fig.6 Battery temperature and temperature difference vary with wind speed in different arrangements.(a) highest temperature,(b) lowest temperature,(c) average temperature,(d) temperature difference.
3.2 方案改进对电池模组散热的影响
根据改进图3,不同方案下电池温度和温差随风速的变化如图7。与长方形排布的电池温度相比,在不同风速下的方案改进后的电池的最高温度、平均温度、温差均降低,而最低温度均增加。

图7 不同方案下电池温度和温差随风速的变化(a)方案1,(b)方案2Fig.7 Variation of battery temperature and temperature difference with wind speed under different schemes (a) scheme 1,(b) scheme 2.
与长方形排列的电池的横向风道模型相比较,在1 C下,当风速为1 m·s-1、2 m·s-1、3 m·s-1、4 m·s-1和5 m·s-1时:对于方案1:最高温度降幅分别为7.29%、9.28%、8.32%、8.20%、7.84%;平均温度降幅分别为0.21%、0.62%、1.06%、1.08%、1.10%;温差降幅分别为51.04%、55.59%、53.64%、54.45%、54.26%。最低温度增幅分别为3.86%、2.52%、1.81%、1.43%、1.10%。
对于方案2:最高温度降幅分别为9.65%、11.06%、10.02%、9.60%、9.18%;平均温度降幅分别为0.39%、0.95%、1.02%、1.08%、1.17%;温差降幅分别为81.85%、79.35%、77.81%、77.50%、77.03%。最低温度增幅分别为8.75%、6.29%、5.15%、4.48%、3.84%。
由以上可知,与电池长方形排列相比,方案2的电池的最高温度、平均温度、温差降幅度明显高于方案1,而最低温度增幅明显高于方案1。
由以上可知,方案2的散热能力较好,为了进一步研究方案2的散热效果,在初始温度25 ℃、3 m·s-1风速条件下,获得了不同放电倍率的温度分布图以及电池温度、温差,如图8和表2。由图8可知,在相同电池单体数量下,接近出风口2侧(见图3)的电池温度相对较高,接近出风口1侧电池温度相对较低。同时,从出风口2侧向出风口1侧,电池温度是逐渐降低,这说明出风口1侧电池散热量比出风口2侧多。另外,由进风口到出风口1,放电倍率影响不同排电池的颜色分布。当1 C、2 C时,电池颜色变化为:深浅黄色→少量深黄色+占主导的浅黄色→少量浅绿色和占主导的浅黄色→少量的绿色和占主导的浅黄色→少量的深蓝色和占主导的中蓝色;3 C时,电池颜色变化为:深浅黄色→少量的绿色和占主导的浅黄色→少量浅绿色和占主导的浅黄色→少量的绿色和占主导的蓝色→深蓝色。在1 C和2 C放电倍率下电池温度中,相对高的温度分布相对较多,而相对低的温度分布相对较少;在3 C放电倍率下电池温度中,相对高的温度分布相对较少,而相对低的温度分布相对较多。由温度云图可获得电池的温度和温度差,如表2。由表2可知,电池的最高温度、最低温度、平均温度和温差的由小到大的顺序为1 C,2 C,3 C。另外,在3种放电倍率下,电池的温差都相差不大,这说明对方案2的电池模型结构,其散热性能相对较好。
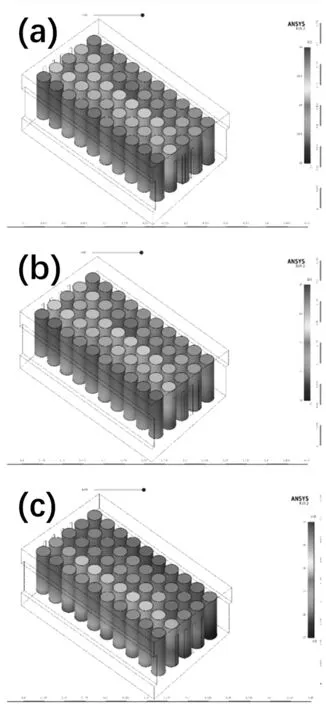
图8 不同放电倍率下方案2温度云图(a)1 C,(b)2 C,(c)3 CFig.8 Temperature nephogram of Scheme 2 at different discharge rates.(a) 1 C,(b) 2 C,(c) 3 C.

表2 不同放电倍率下方案2的电池温度变化Table 2 Changes of cell temperature in scheme 2 at different discharge rates.
4 结论
(1)在相同风速下,横向风道模型的电池温差低于纵向风道模型的电池温差。
(2)随着风速增加,电池的最高温度、平均温度和温差均降低。风速大于1 m·s-1时,电池的温差由大到小的排列顺序为:错开排列、长方形排列、双梯形排列、梯形排列。
(3)散热比较好的风道模型是:横向风道/一个进风口+二个出风口(一个在进风口侧,一个在进风口对面壁上)+两侧风口壁上分别开设四个散热孔。由一个进风口+两侧壁面上分别开设4个散热孔。该风道模型电池的最高温度、平均温度、温差降幅度较大;在设置的放电倍率下,电池的温差仅为1.34 ℃~4.0 ℃。
