基于MRE 隔振器的变刚度半主动隔振系统分析

2021-09-27黄学功刘涛马伟佳张广

湖南大学学报（自然科学版） 2021年8期

黄学功，刘涛，马伟佳，张广

（南京理工大学机械工程学院，江苏南京 210094）

磁流变弹性体（Magnetorheological Elastomer，MRE）是磁流变材料的一种，一般是在基体材料（如橡胶等高分子聚合物）中添加微米级的软磁性颗粒，经过一系列工序制成[1-3].1996 年Jolly 团队[4]首次将软磁颗粒加入到高分子聚合物中得到了最初的磁流变弹性体，并测试得到了磁流变弹性体在施加磁场后的力学性能变化响应时间为毫秒级别.加拿大学者Dargahi 等[5]用硅橡胶作为基体，加入体积分数为40%的羰基铁粉制成磁流变弹性体材料，当磁感应强度从0 T 增加到0.45 T 时，相对磁流变效应达到了1 672%.近年来，随着磁流变弹性体性能的提升，其响应速度快、高磁流变效应的特点受到了越来越多的关注，已经成为土木工程、结构振动控制领域研究的热点.

磁流变弹性体隔震支座使用磁流变弹性体材料代替传统橡胶材料，可以通过磁感应的强弱来改变支座的刚度，相较于传统橡胶隔震支座拥有了可控性.悉尼科技大学的Li 等[6]和Gu 等[7]根据传统的叠层橡胶隔振器设计了一款叠层MRE 隔振支座，并进行了一系列实验研究，根据测试，该隔振器的最大水平剪切位移为26 mm，在零磁场强度的情况下纵向承载力可达到370 kg.马来西亚理工大学的Wahab等[8]利用天然橡胶基MRE 制作了一台大型的应用于实际建筑隔振的基础隔震支座，其中详细介绍了支座的设计加工过程，MRE 叠层结构的焊接工艺，具有很高的实用价值.测试表明，当工作电流从0 A 增加到3 A 时，支座的静态竖向承载力增加了14%，动态竖向承载力增加了16%.

现有研究中，磁流变弹性体隔震支座大多采用半主动控制机制.近些年，国内外学者对基于磁流变弹性体隔震支座的半主动控制算法进行了大量研究.Eem 等[9]提出基于模糊控制的半主动控制算法，并通过试验，验证了其对结构的减震效果.Xu 等[10]提出了基于磁流变弹性体隔振支座的改进半主动变刚度控制算法，该算法充分利用支座的连续变刚度特性，控制效果良好.悉尼科技大学的Gu 等[7]提出了基于神经网络控制的模糊控制算法，并进行了隔振控制试验，结果表明，该控制算法有很好的控制效果.

目前对MRE 隔振器的研究大多为正向变刚度MRE 隔振器，对负刚度MRE 隔振器的研究较少.负刚度MRE 隔振器有效解决了正向变刚度MRE 隔振器在没有振动的情况下也需要一直通电的问题，更加符合实际工程应用要求，因此对负刚度MRE 隔振器进行全面研究具有极高的工程价值.本文基于制备的磁流变弹性体材料，设计了一款面向横向振动的负刚度隔振器，并进行了性能测试试验.基于负刚度隔振器搭建了变刚度半主动隔振控制系统，设计了GA 模糊控制算法并进行了仿真分析.

1 MRE 隔振器设计与试验方法

1.1 磁流变弹性体制备与测试

1.1.1 磁流变弹性体制备

磁流变弹性体的制备分三个过程：材料的充分混合、预磁化处理以及室温下的固化.具体过程如图1 所示，先将羰基铁粉、硅橡胶和二甲基硅油按质量比为8 ∶1 ∶1 倒入烧杯中，充分搅拌使其混合均匀；然后将材料放入真空桶，抽出材料中的气泡，这一步需反复多次抽取；倒入模具，盖上模具端盖，放在磁感应强度为600 mT 的加磁装置中进行预磁化处理，预磁化的目的是为了提高MRE 的磁流变效应，研究表明，预磁化的MRE 可以产生更加明显的磁流变效应以及更大的磁致模量[11]；加磁2 h 后放置常温干燥环境5～7 d，即能脱模完成MRE 样品的制备.

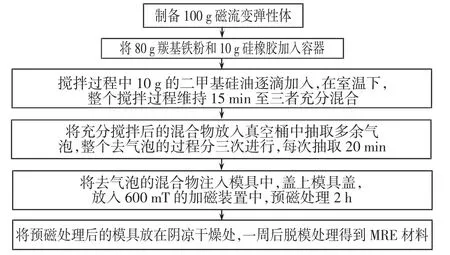
图1 MRE 制备过程Fig.1 MRE preparation process

1.1.2 磁流变弹性体性能测试

将制备好的MRE 样品置于如图2 所示的测试仪器中，测试仪器为流变仪（型号：MCR302，Anton Paar），根据仪器的要求，将MRE 材料制成直径为20 mm，厚度为1 mm 的圆形薄片，将MRE 样品置于转子与下盘片之间.由于MRE 要应用于MRE 隔振器中，在工作过程中处于动态应变条件，需要研究MRE 材料在动态应变下的特性才能更好地服务于MRE 隔振器.整个测试过程，MRE 薄片处于剪切工作模式，这与后续的隔振器工作模式一致.通过计算机设定室温下测量，流变仪自带的温控系统可以设置温度恒定；设置不同的工作条件，然后将测试结果存档.本次测试MRE 性能的测试条件为：室温25 ℃恒定，测试频率设置为8 Hz，应变条件设置为0.1%、0.5%、1%.磁场强度从0 T 开始持续增加，直到MRE材料的储能模量趋于稳定不变为止.

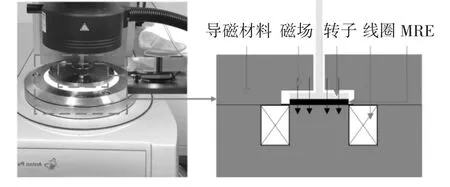
图2 流变仪测试原理Fig.2 Testing principle of rheometer

图3（a）为在不同应变条件作用下MRE 的剪切储能模量与磁感应强度之间的关系.从图中可以看出，MRE 的剪切储能模量随磁感应强度呈非线性增长趋势，在磁感应强度为600 mT 时趋于稳定，在800 mT 时达到稳定值.其中在0.1%应变条件下储能模量最大，达到2.95 MPa，随着应变的增加，储能模量会随之降低，当应变为1%时，储能模量最大为2.15 MPa，较0.1%应变条件，储能模量衰减了27.6%，随着应变的增大，衰减会更加严重，这是Payne 效应造成的，随着应变的增加，粘弹性材料的动态模量会减小.图3（b）是不同应变条件下MRE的磁流变效应随磁感应强度的变化图，从图中可以看出，在小应变情况下，磁流变效应很大.当应变条件为0.1%时，磁流变效应最大可达到2 040%.换言之，在该应变条件下，当磁感应强度达到600 mT 以上时，MRE 的剪切储能模量增加了20 倍.高磁流变效应是实际工程应用的关键，可以让磁控条件降低，降低了外部磁场发生装置的设计难度.

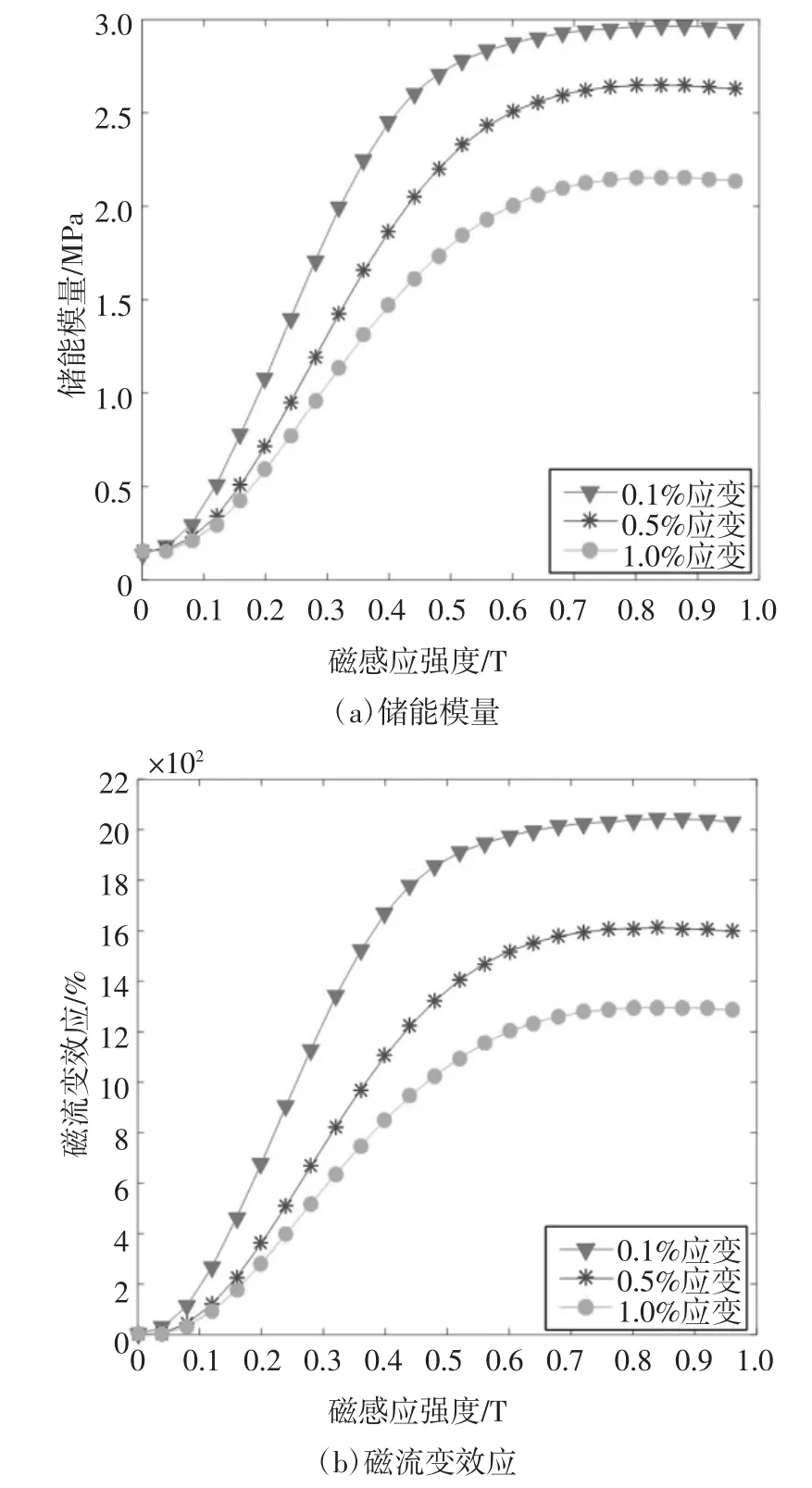
图3 材料特性与磁场关系Fig.3 Relationship between material properties and magnetic field

1.2 MRE 隔振器的设计与测试

1.2.1 MRE 隔振器的设计

隔振器的具体设计过程参考文献[12].隔振器的实物模型、具体结构组成以及工作原理如图4 所示.其中永磁铁提供一定大小的磁场，使隔振器具有较大的初始刚度，在正常工作环境中能够承受较大的载荷，通过调节通入线圈电流的大小来改变隔振器的内部磁场环境，核心部分就是MRE 叠层结构，通过内部磁感应强度的大小来改变此结构的刚度和阻尼大小，进而达到隔振的目的.

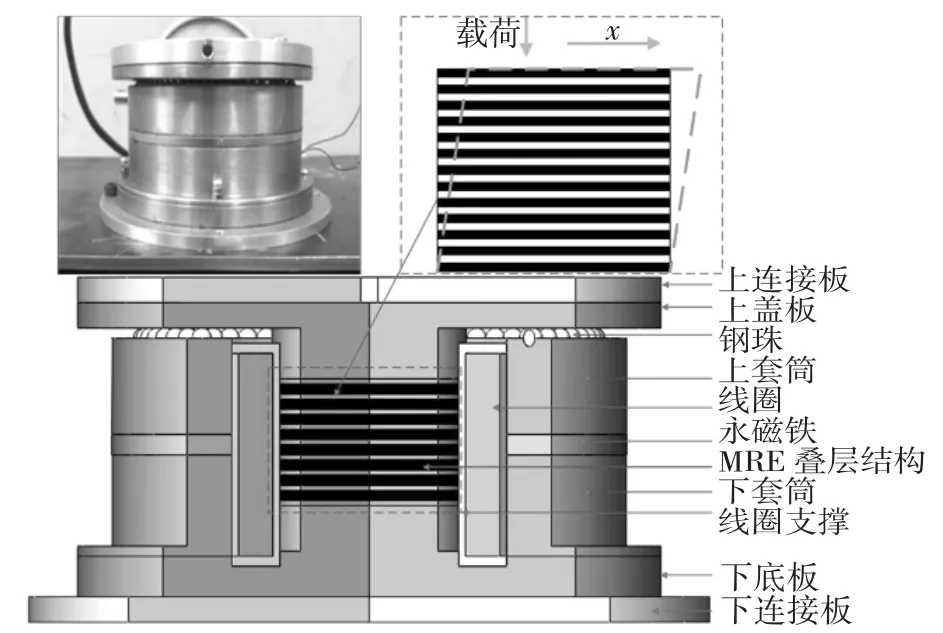
图4 隔振器结构及原理Fig.4 Structure and principle of vibration isolator

1.2.2 MRE 隔振器的移频特性测试

由于MRE 隔振器的固有频率随着外加磁场的变化而连续、快速变化，为了更好研究其隔振性能及其隔振控制规律，有必要进行相应的试验来对其移频特性进行测试.图5 为本文所搭建的MRE 隔振器移频特性测试试验平台，信号发生器发出的信号经由功率放大器放大后驱动激振器推着水平滑台进行受迫振动，MRE 隔振器安装于水平滑台之上，两个加速度传感器分别安装于MRE 隔振器上和水平滑台上，用于测得激励和响应加速度信号，所测得的加速度信号经电荷放大器转变为电压型加速度信号后传入LMS 动态测试系统，LMS 动态测试系统对信号进行分析处理后最终传至PC，整个过程中，由直流电源给MRE 隔振器供电.

图5 移频特性测试平台Fig.5 Frequency shift characteristic test platform

根据试验数据得到如图6 所示的加速度传递率曲线，在-3 A、-1 A、1 A、3 A 电流下隔振器的共振频率分别为68 Hz、63 Hz、59 Hz 和50 Hz.因此，可以得出在-3～3 A 的电流范围内MRE 隔振器的共振频率随着励磁电流的增加而减小，由-3 A 时的68 Hz 减小到3 A 时的50 Hz，减小了18 Hz，隔振器的共振频率发生了明显的负向移频.这是由于作用于MRE 的磁场是由励磁电流激发的磁场和永磁体所产生的磁场叠加而成的，当两个磁场的方向相反且励磁电流所激发的磁场小于永磁体的矫顽力时，励磁电流的值越大，叠加磁场的强度就越小，MRE 的刚度就越小，从而隔振器的共振频率就越小.当两个磁场的方向相同时，励磁电流的值越大，叠加磁场的强度就越大，MRE 的刚度就越大，从而隔振器的共振频率就越大.

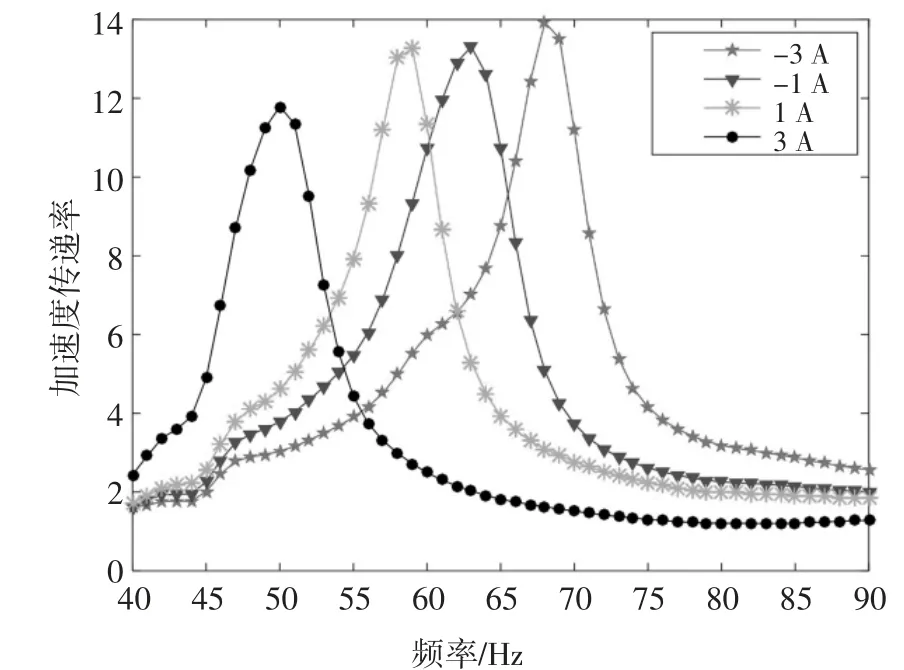
图6 移频特性曲线Fig.6 Frequency shift characteristic curve

1.2.3 MRE 隔振器的参数计算

隔振器的简化模型可以用一个单自由度模型来描述，如图7 所示.根据模型可以建立运动方程：

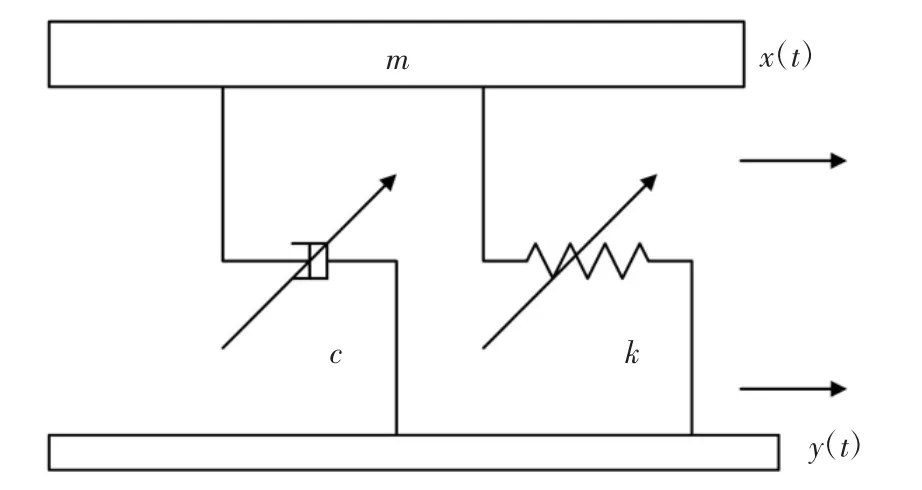
图7 隔振器单自由度模型Fig.7 Single degree of freedom model of vibration isolator

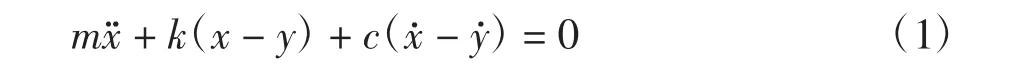
式中：m 为负载质量；k 和c 分别为MRE 隔振器的刚度和阻尼；y 和x 分别为激励位移和响应位移；y和x分别为激励速度和响应速度；x 为响应加速度.

已知单自由度有阻尼系统的传递率函数表达式为：

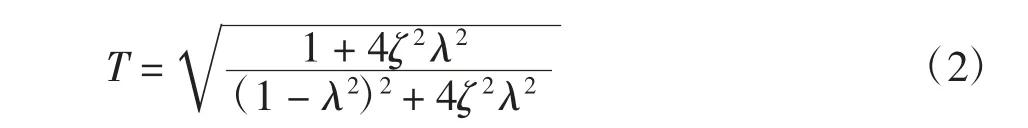
对于有阻尼单自由度振动系统来说，其共振频率为：

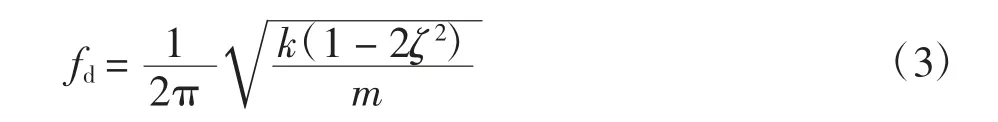
式中：fd为该隔振系统的共振频率.

通过式（2）计算得到的系统阻尼比ζ 和试验测得的共振频率fd，利用式（3）可以计算系统的等效刚度，再由阻尼比公式可以得到系统的等效阻尼.

本次测试的负载质量为0.75 kg，结合图6 可以得到MRE 隔振器在不同电流下的性能参数如表1所示.Tm为传递率最大值，从表1 可以看出，随着电流的增加，隔振器的刚度和阻尼随之减小.其中，变刚度特性明显，阻尼变化不明显.图8 为隔振器刚度随电流变化曲线，由图8 可得，刚度随电流基本呈线性变化关系，拟合曲线的关系式为：

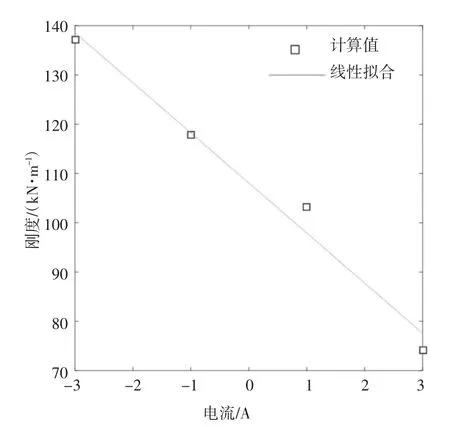
图8 刚度线性拟合曲线Fig.8 Stiffness linear fitting curve

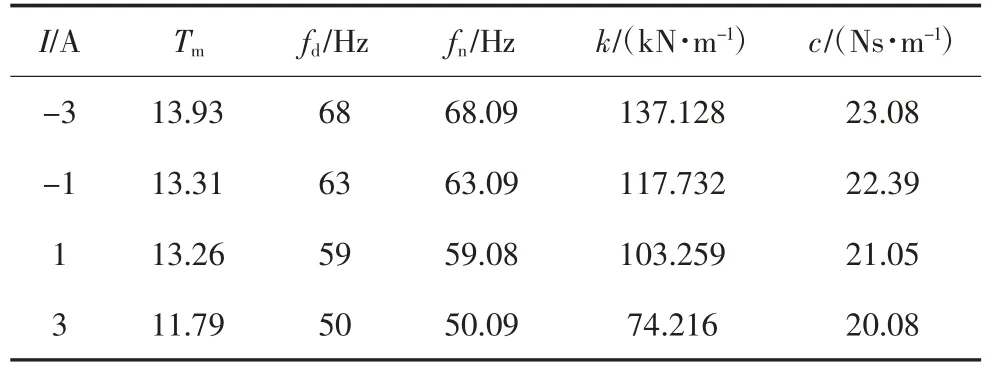
表1 MRE 隔振器的性能参数Tab.1 Performance parameters of MRE isolator

2 基于MRE 隔振器的半主动隔振系统

2.1 地震作用下变刚度隔振系统的动力模型

对于层数较多的钢筋混凝土框架和钢架结构，在地震波的作用下，上层结构的变形以剪切变形为主，为了准确计算出各层的响应情况，可采用多质点计算模型来模拟建筑结构[13].建立多质点模型有三个假定条件：刚性地基，即各点水平运动完全一致；各楼层质量集中在一点；做纯剪切运动.具体的模型结构如图9 所示.

根据达朗贝尔原理，图9 的隔震模型在地震波作用下的运动方程可表示为[14]：

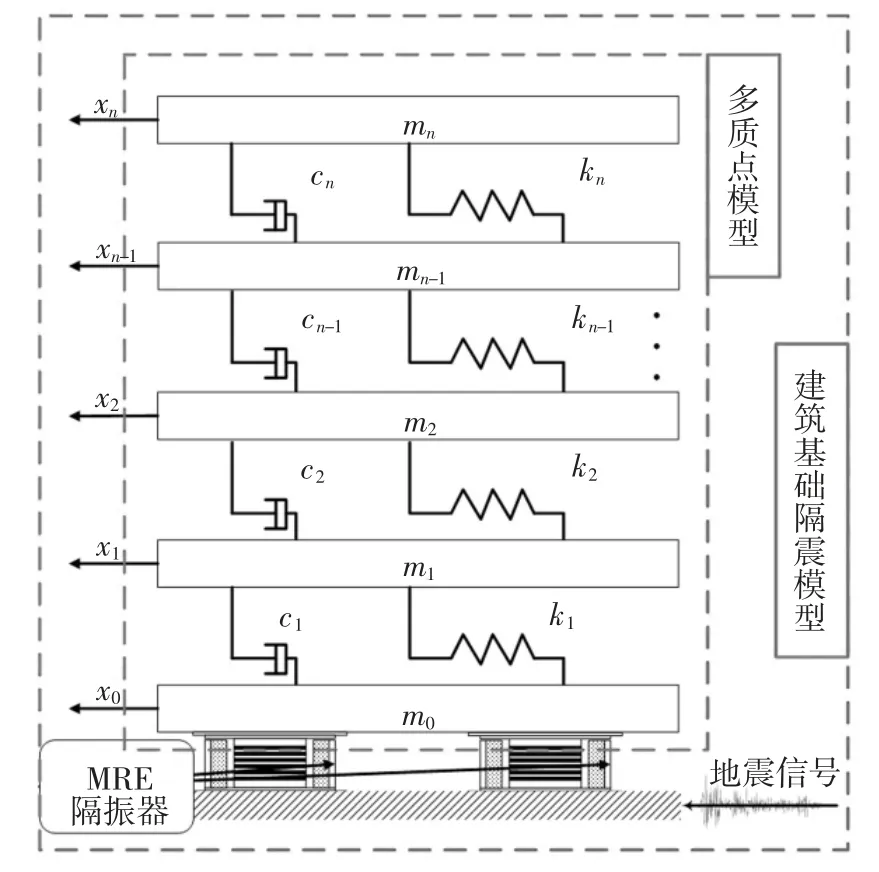
图9 基础隔震模型Fig.9 Base isolation model

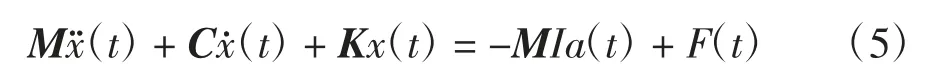
式中：M、K、C 分别为结构的质量、刚度以及阻尼矩阵；x（t）为位移响应；a（t）为地震加速度；F（t）为控制力.I=[1 0 0 …]T1×n.

阻尼采用Rayleigh 阻尼[15]，计算公式如下：

α 和β 为比例系数.

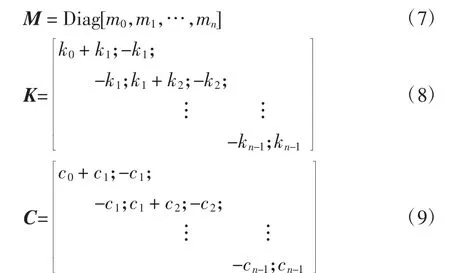
由MRE 隔振器以及电流变化产生的控制力F（t）可表示为：

由式（4）可知：

控制力由隔振器输出直接作用于建筑的隔震层，可令

式中：m0为隔振层的质量；a0为控制力产生的加速度.

将式（12）代入式（5）可得

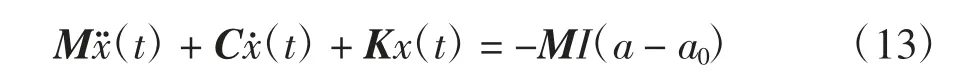
2.2 控制算法

2.2.1 On-off 控制

由表1 可知，隔振器刚度随电流变化明显，基于这种特性选用On-off 控制策略进行半主动控制，内容如下[16]：

式中：kmax，kmin为隔振器的最大刚度和最小刚度.当激励开始时，如果x·≥0，即被控对象偏离并且有偏离更远的趋势时，需要增大隔振器的刚度从而抑制这种运动趋势；当x·＜0 时，被控对象趋近平衡位置，将隔振器刚度调到最小，使其慢慢回归平衡位置.

2.2.2 模糊控制

模糊控制器包括模糊化、推理机制、模糊规则和解模糊.其中e 作为负载相对位移偏差，是负载位移变化率，e 和作为模糊控制器的输入，输出电流I 作为施加在励磁线圈的电流.输入论域设置为[-3，3]，输出论域设置为[-3，3]，将输入输出变量划分为7 个模糊等级.输入量的隶属函数选择Gaussmf 型，可以提升模糊控制的平滑性，输出量隶属函数选择三角型，可以提高控制器的灵敏度，模糊推理机制采用Mamdani 理论，用重心法进行解模糊.模糊规则见表2.

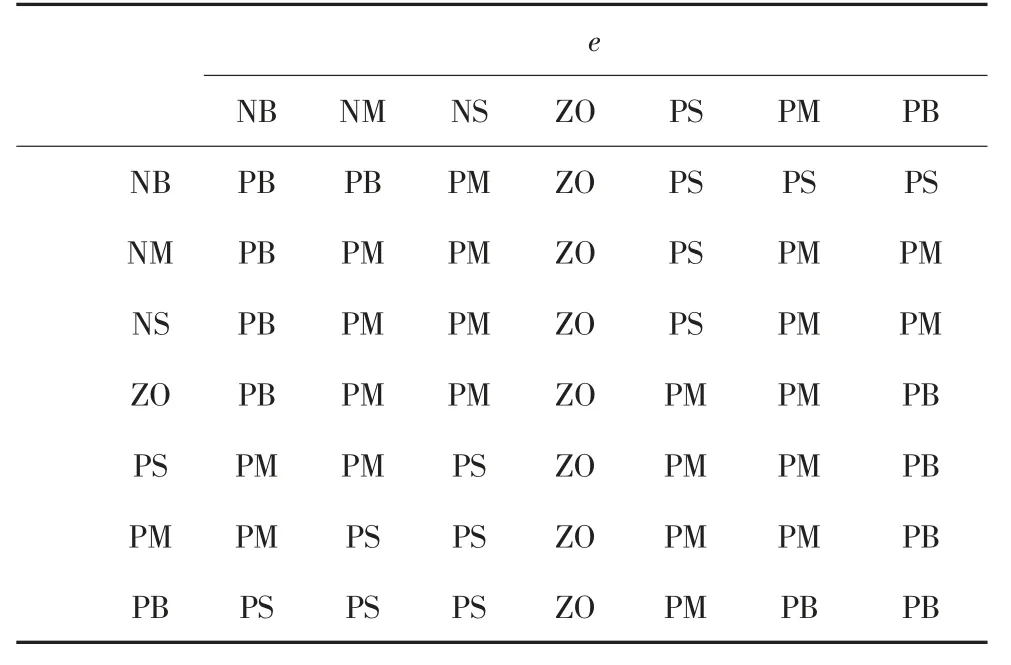
表2 控制规则表Tab.2 Control rule table

2.2.3 遗传模糊控制

遗传算法基于自然选择、适者生存的遗传思想，具有对问题依赖性小和全局寻优的特点，可应用于模糊控制器的优化.基于上节的模糊控制器，对其隶属函数进行优化，进而与优化前的模糊控制器控制效果进行比较.

输入采用的Gaussmf 型隶属度函数，函数的表达式为：

每一个隶属函数由两个参数确定，在双输入系统中，每个输入有7 个模糊子集，所以一共需要优化28 个参数.

考虑到位移是与安全性有关的参数，本文以结构的位移响应作为评价标准，适应度函数为：

遗传算法的具体参数设置为：种群规模为100，迭代次数为300，交叉概率和变异概率分别为0.9 和0.1.以输入为EI-Centro 地震波为例，表3 是优化后得到的隶属度函数参数，图10 是优化前后隶属度函数曲线对比，图11 是优化前后输入输出曲面图对比.从图11 中可以看出，优化后，当模糊控制器的输入较大时，可以输出更大的控制电流，当模糊控制器的输入较小时，输出的控制电流可以控制得更小，优化了控制效果.

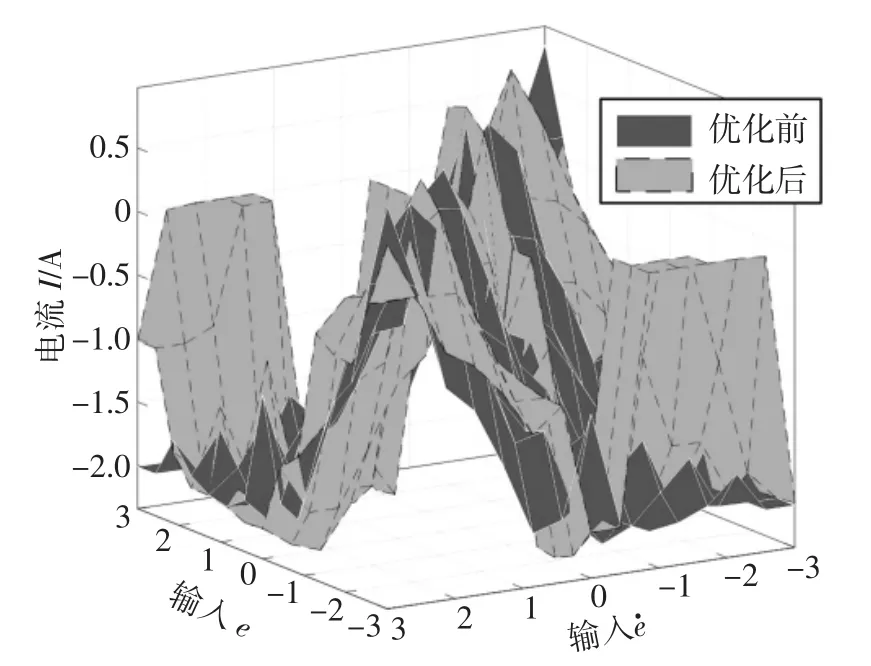
图11 优化前后输入输出曲面图Fig.11 Input and output surface maps before and after optimization

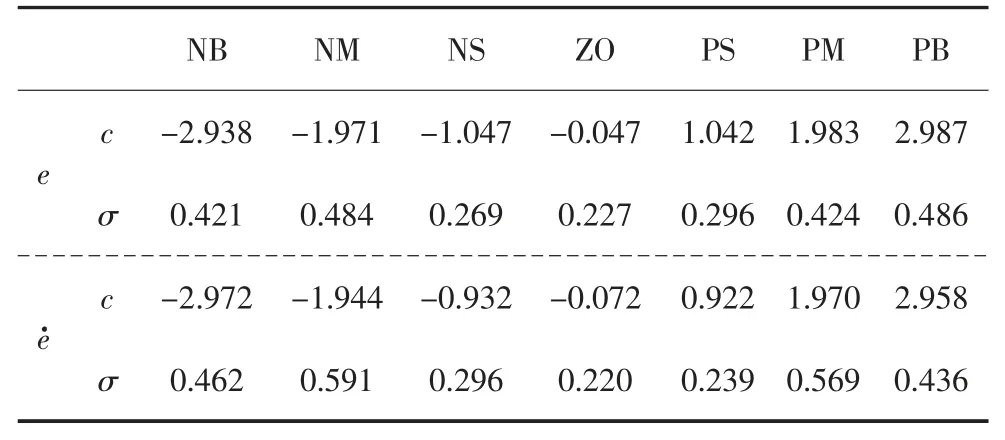
表3 优化后隶属度参数Tab.3 Membership parameters after optimization

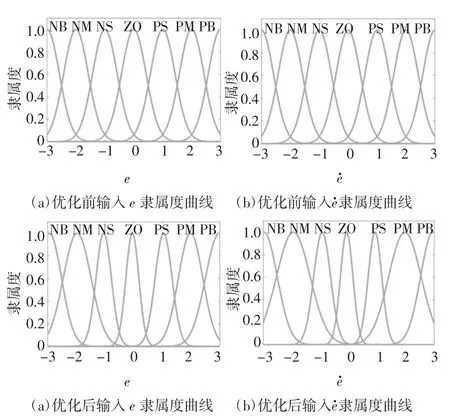
图10 优化前后隶属度函数曲线Fig.10 Membership function curve before and after optimization

3 仿真分析

为了验证MRE 隔振器在变刚度半主动隔振系统中的隔振效果，选取了抗震设防烈度为8 度的某4层商店-住宅砌体结构房屋为例.在EI-Centro 波、Taft 波以及人工地震波的作用下，对其结构进行地震激励仿真分析，地震波的采样时间为2 ms，将地震波的加速度幅值设为4 m/s2.建筑结构参数如表4 所示.根据隔振器刚度随电流变化规律，拟采用20 个MRE 隔振支座，单个支座的刚度为3.4×105kN/m，得到隔震层的总刚度为6.8×105kN/m.根据式（14）系统状态方程以及图12 所示的隔振控制系统，可以建立Simulink 模型进行数值仿真分析.

表4 建筑结构参数Tab.4 Building structure parameters

图12 隔振控制模型Fig.12 Vibration isolation control model

根据图12 搭建Simulink 动态仿真模型，如图13 所示.将EI-Centro 波、Taft 波以及人工波三种波作为激励，嵌入上文提到的On-off 控制、模糊控制以及GA 模糊控制三种控制算法，观察各自的响应情况.三种地震波的加速度时程曲线如图14 所示.图15 为仿真结果，顶层的位移响应时程曲线.

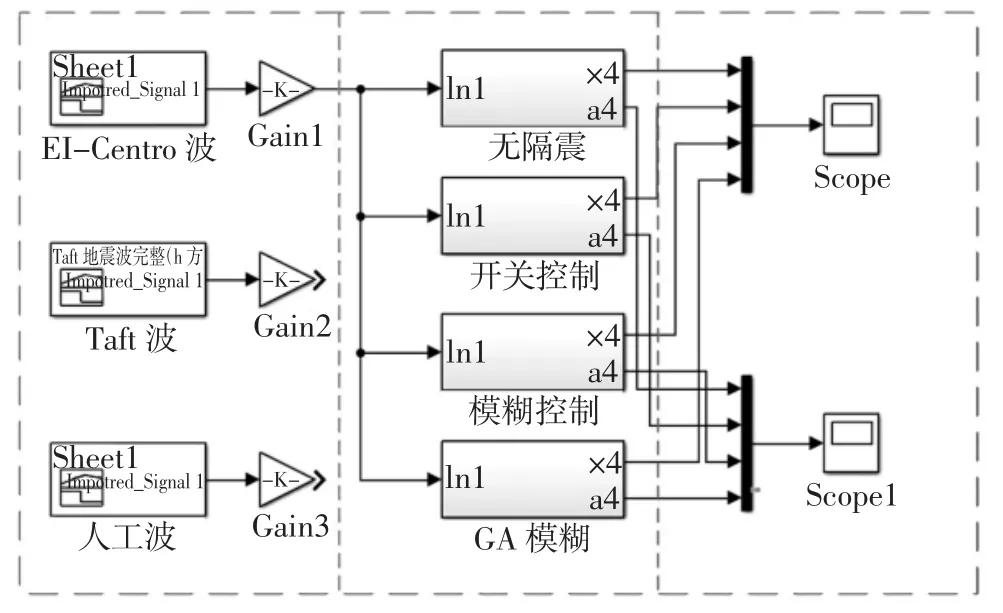
图13 Simulink 动态仿真模型Fig.13 Simulink dynamic simulation model

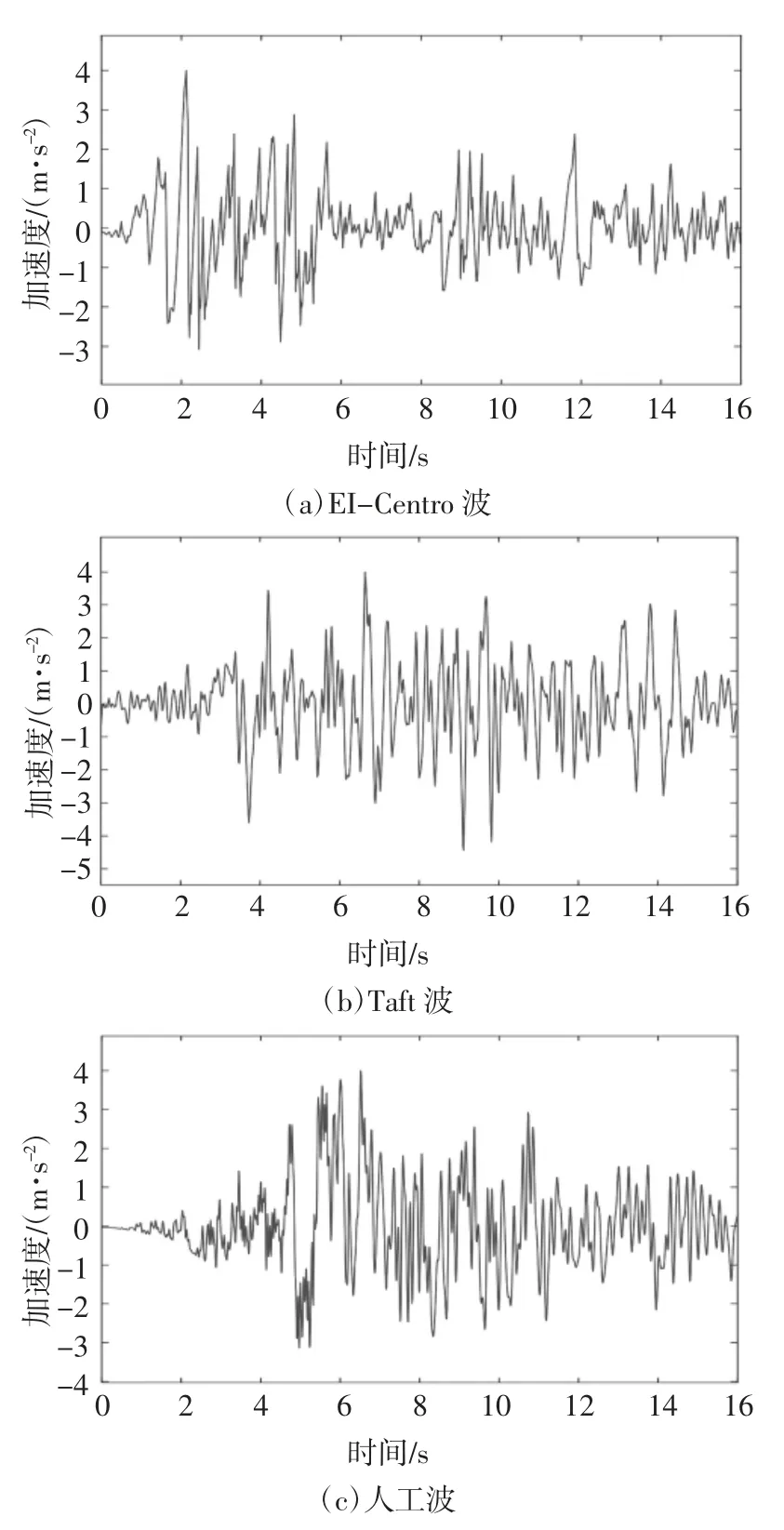
图14 地震波时程曲线Fig.14 Seismic wave time history curve

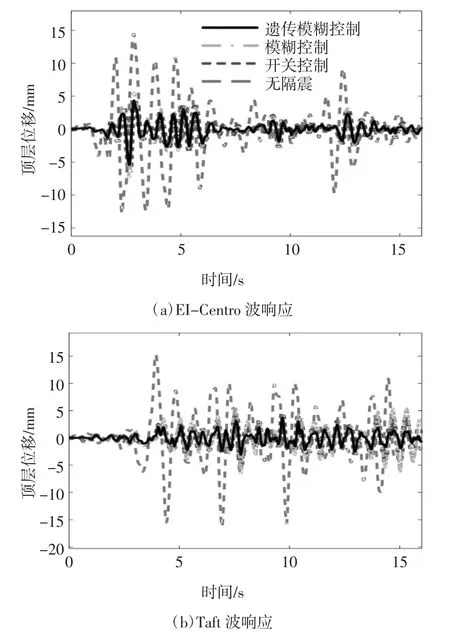
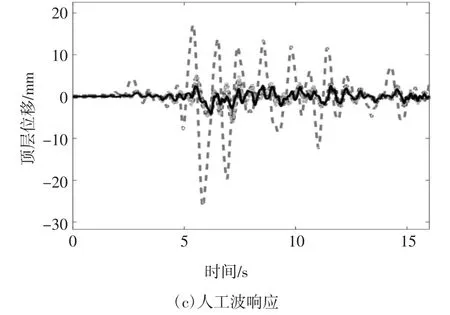
图15 结构响应时程曲线Fig.15 Time history curve of structural response

从图15 中可以看出结构在三种控制策略的作用下，顶层的位移响应都具有明显的下降趋势，说明了MRE 隔振器可用于对建筑的隔振.通过位移响应对比发现，经过遗传算法优化的模糊控制器大大提高了控制性能.根据位移响应曲线，提取出各层位移的响应峰值以及位移RMS（Root Mean Square）值得到下表数据.表5、表6 和表7 分别是建筑结构在三种地震波作用下各层位移响应的峰值以及RMS 值，图16 是位移控制效果对比图.

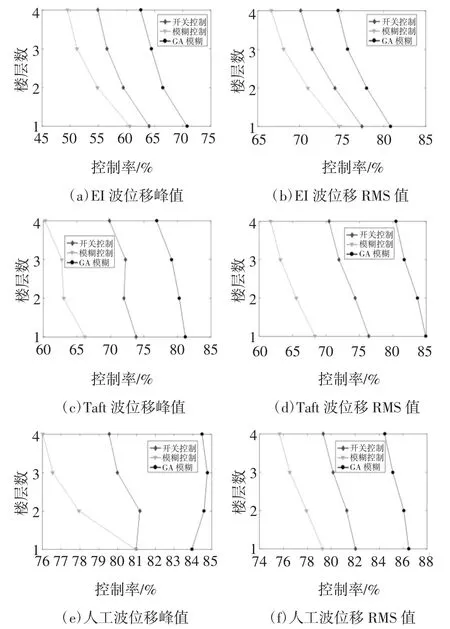
图16 控制效果对比图Fig.16 Control effect comparison chart

表5 EI-Centro 波作用下结构各层位移峰值及RMS 值Tab.5 Structural displacement peak and RMS under EI-Centro wave

从上图表中可以看出，三种半主动控制策略对结构的位移响应都具有较好的控制效果，对位移峰值的控制效果达到50%以上，对位移均方根值的控制效果到达了60%以上.对位移均方根的控制效果优于对位移峰值的控制，这说明对激励过程的整体控制更好.楼层越高，三种控制效果就会越差.三种控制策略对人工波的控制效果最好，对EI-Centro 波的控制效果最差.经过遗传算法优化后的模糊控制器控制效果改善明显，提升了10%以上.整体上Onoff 控制优于模糊控制，但是On-off 控制在工作时是持续输出最大电流，相比较而言，模糊控制可以节省更多的能源，GA 模糊控制在输出电流方面更加合理，控制效果更好，在实际工程中有应用的潜力.