设置线性磁流变可控阻尼框架结构的半主动控制分析

付熊 张敏 陈钰雪 邵海浪

摘  要：为研究框架结构地震反应，采用磁流变阻尼器对其进行半主动控制分析.首先使用控制理论建立能同时控制位移、速度和加速度的主动控制方程，并推导了最优控制力，通过算例探讨了框架结构位移、速度和加速度的权函数;然后对设置可控阻尼器的10层框架结构进行地震反应半主动控制分析，研究了结构位移、速度和加速度等地震响应，由此分析可控阻尼器最大和最小阻尼系数对半主动控制的影响.结果表明：应考虑能量消耗合理选择结构控制的各权函数，并应合理设置可控阻尼器最大和最小阻尼系数.算例表明，最小阻尼器系数可取为最大阻尼系数的1/10，以使框架结构获得较优的控制效果.

关键词：可控;磁流变;阻尼;半主动;主动控制;最优

中图分类号：TU352.11               DOI：10.16375/j.cnki.cn45-1395/t.2021.01.013

0    引言

地震是一种强大的自然灾害，会对建筑房屋造成巨大的破坏.为了满足现代社会对安全性、适用性和可靠性的要求，不少学者对建筑消能减震技术进行了大量研究，其研究领域主要分为3个：基础隔震、被动耗能减震以及主动控制等[1-2].    1972年，美国Yao结合现代控制理论，提出了土木工程结构振动控制概念，开创了结构振动控制研究新里程[1].之后，不少学者对主动控制，智能控制和半主动控制进行了研究，表明主动控制效果最好，但需要消耗大量外部能量.半主动控制结合了主动控制和被动控制的优点，无需消耗过多的能量就可实现对结构振动反应控制，因此，引起了不少土木工程专家的关注.孙清等[3-4]通过对不同结构进行地震激励分析，不同试验表明了采用半主动控制效果接近主动控制，且优于被动控制.Ferreira等[5]在结构和调谐质量阻尼器之间添加半主动控制阻尼器组成后的半主动调谐质量阻尼器结构，其控制效果较单一的调谐质量阻尼器好.陈超[6]研究表明，对半主动阻尼器而言，不同的控制策略将对阻尼器的控制效果影响较大.林伟等[7]研究表明（TIOC）半主动控制算法可以显著降低结构的地震响应.张志强等[8]分析表明了嘉绍大桥的控制效果随着磁流变阻尼器数量的增加而增强，但阻尼器数量达到一定程度，控制效果增加的幅度越来越小.陈水生等[9]在斜拉索中应用速度和位移的半主动控制算法，表明该算法简单，且控制效果优于被动控制，但最优控制算法未考虑结构加速度.李歆等[10]提出了改进的Bang-Bang半主动控制策略，但控制策略的能量方程只考虑了位移和速度，未涉及加速度. 张敏[11]提出了能够同时控制位移、速度和加速度的控制策略，并对设置磁流变阻尼器的巨型框架结构进行半主动控制分析，但未探讨磁流变阻尼器系数对半主动控制的影响.

目前大多数研究的最优控制策略主要采用位移反馈或者位移、速度联合反馈，但很少涉及同时控制结构位移、速度和加速度的策略.本文推导能同时控制结构位移、速度和加速度的控制策略，通过算例探讨影响主动控制效果的位移、速度和加速度的权函数;最后对一个设置磁流变阻尼器的10层框架结构进行主动和半主动控制分析，并研究了最大和最小阻尼系数对半主动控制效果的影响，从而为可控阻尼器设计提供参考.

1    可控阻尼状态方程

一个有n个楼层结构设置[P]个可控阻尼器的装置，在地震作用下，结构振动方程为：

式中：[M]、[C]和[K]分别为结构自身的质量矩阵、阻尼矩阵和刚度矩阵;[X（t）]、[X（t）]和[X（t）]分别为各楼层相对于其基础的位移、速度和加速度向量;[Pt]为可控阻尼器的控制力向量;[xg（t）]为地面运动加速度;[1]为元素为1的列向量.

4    可控阻尼半主动控制策略

结构变阻尼控制算法有多种，如简单Bang-Bang控制算法、最优Bang-Bang控制算法和限界Hrovat最優控制算法等[1-2].一般各算法中阻尼器第[i]时刻的阻尼系数[cdi]均在最小阻尼系数[cdmin]和最大阻尼系数[cdmax]之间变化.本文可控阻尼器的阻尼系数选取合适的最小值与最大值，并根据下列策略将前述所求最优阻尼系数进行调整，从而获得可控阻尼半主动控制策略.

5    算例

5.1   主动控制权重分析算例

该算例参考文献[1]，为一个3层框架结构，每层质量均为[m=4×105] kg，层间刚度均为k [=2×108] N/m，结构阻尼比为[ξ=0.05]，结构的外干扰为EI-Centro地震波，地震输入峰值为200 cm/s2.

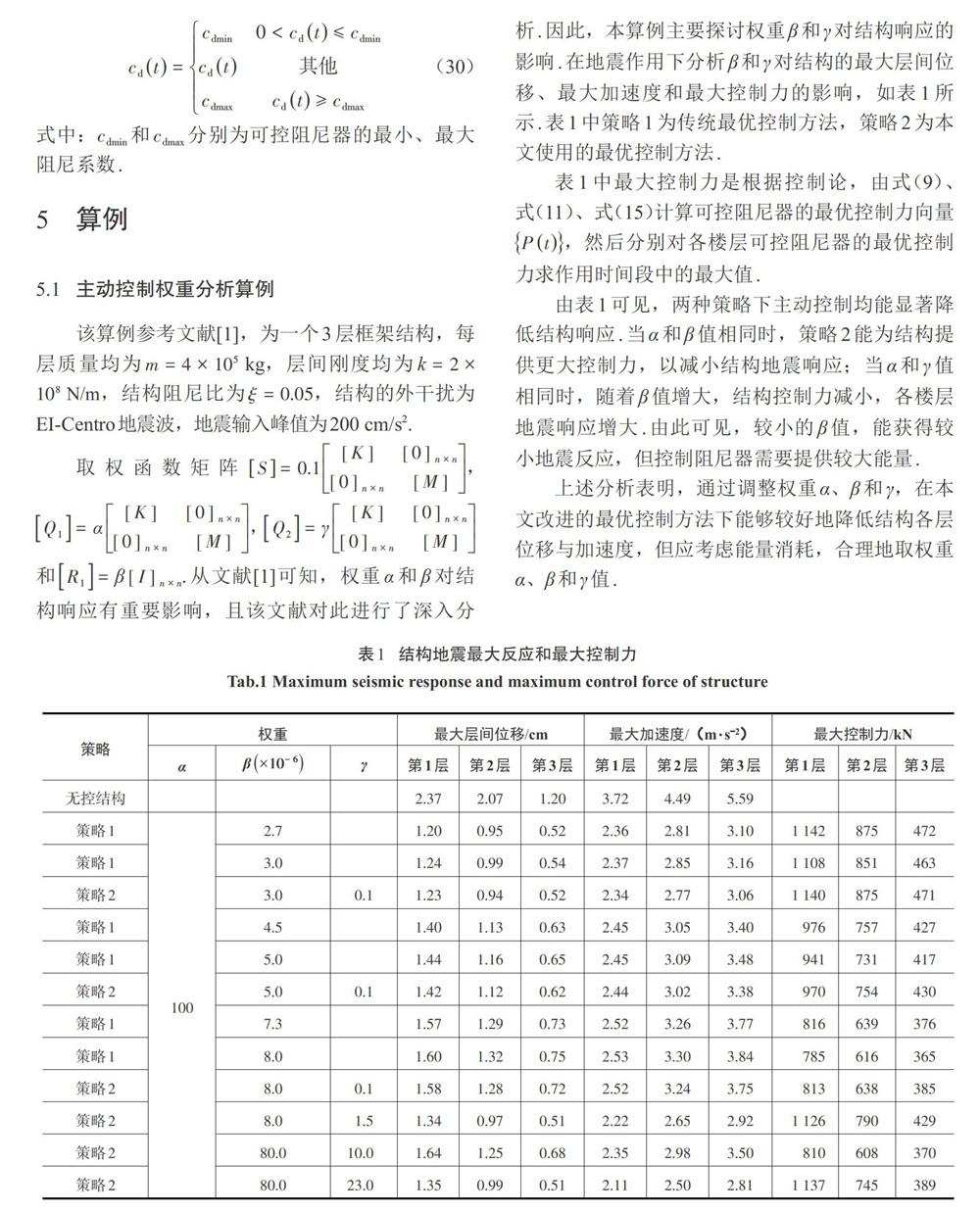
取权函数矩阵[S=0.1[K][0]n×n[0]n×n[M]]，[Q1=α[K][0]n×n[0]n×n[M]]，[Q2=γ[K][0]n×n[0]n×n[M]]和[R1=β[I]n×n].从文献[1]可知，权重[α]和[β]对结构响应有重要影响，且该文献对此进行了深入分析.因此，本算例主要探讨权重[β]和[γ]对结构响应的影响.在地震作用下分析[β]和[γ]对结构的最大层间位移、最大加速度和最大控制力的影响，如表1所示.表1中策略1为传统最优控制方法，策略2为本文使用的最优控制方法.

表1中最大控制力是根据控制论，由式（9）、式（11）、式（15）计算可控阻尼器的最优控制力向量[Pt]，然后分别对各楼层可控阻尼器的最优控制力求作用时间段中的最大值.

由表1可见，两种策略下主动控制均能显著降低结构响应.当[α]和[β]值相同时，策略2能为结构提供更大控制力，以减小结构地震响应;当[α]和[γ]值相同时，随着[β]值增大，结构控制力减小，各楼层地震响应增大.由此可见，较小的[β]值，能获得较小地震反应，但控制阻尼器需要提供较大能量.

上述分析表明，通过调整权重[α]、[β]和[γ]，在本文改进的最优控制方法下能够较好地降低结构各层位移与加速度，但应考虑能量消耗，合理地取权重[α]、[β]和[γ]值.

5.2   半主动控制算例

該工程由文献[12]可知，为一栋10层混凝土框架结构楼，底层层高4.5 m，其余各层层高均为3.3 m，结构总高度为34.2 m.该结构设防类别为丙类，抗震设防烈度为9度，基本地震加速度为400 m/s2，设计地震分组为第2组.结构自身阻尼比                  ζ=0.05，混凝土强度等级为C30，楼屋面折算恒载标准值为10 kN/m2（包括墙体自重），楼屋面活载标准值为2 kN/m2.梁截面尺寸为300 mm×650 mm，柱截面尺寸为600 mm×750 mm.结构承受El-Centro地震波（适用Ⅱ类场地），并根据《建筑结构抗震规范》[13]调整地震最大加速度幅值为140 cm/s2.框架结构局部平面布置如图1所示，框架结构各层均布置磁流变可控阻尼器，计算简图如图2所示.

本算例主动控制策略权函数矩阵见5.1算例，其中权重分别取为[α] =100，[β] =1，[γ] =0.3.参考目前磁流变可控阻尼器的阻尼系数取值范围，选取了目前可在工程中应用的可控阻尼器的最大阻尼系数，并参考该阻尼器的阻尼系数可控范围，选取各磁流变阻尼器阻尼系数的最小值和最大值，如表2所示.根据前述各公式，并由表2编制计算机分析程序，可得各阻尼系数下结构的地震响应.无控、主动控制和半主动控制下结构楼层最大位移、楼层最大层间位移角、楼层最大速度、楼层最大加速度以及结构楼层顶层位移时程和顶层加速度时程分别如图3—图8所示.

从图3和图4可知，半主动控制1的楼层最大位移和层间最大位移角均接近主动控制，半主动控制2的结构响应稍大于半主动控制1;半主动控制3和4的楼层最大位移和层间最大位移角接近且略小于无控.

从图5可知，半主动控制1的楼层最大速度小于半主动控制2，且两者的最大速度稍小于主动控制;半主动控制3和4的楼层最大速度接近，且小于无控.

从图6可知，半主动控制1和2的楼层最大加速度接近，但半主动控制2顶层最大加速度发生突变，在楼层中下部，两者的楼层最大加速度小于主动控制，而其余楼层稍大于主动控制;当楼层较低时，半主动控制3的楼层最大加速度小于主动控制，而其余楼层的最大加速度大于主动控制;半主动控制4的楼层最大加速度界于主动控制和无控之间.

从图7和图8可知，除半主动控制3和4的楼层位移接近主动控制外，其余控制对楼层位移均有较好的控制.在楼层加速度控制上，半主动控制3和4控制效果稍弱于主动控制、半主动控制1和2等，但均小于无控.

上述分析表明，磁流变阻尼器最大阻尼系数对结构响应影响较大.随着阻尼器最小阻尼系数的增大，结构响应能得到较好的控制，但当阻尼器最小阻尼系数超越一定数值，结构地震反应的控制效果几乎提高不大;随着最大阻尼系数减小，结构响应会增大并逐渐接近无控结构.因此，为了使磁流变阻尼器具有较大的调节能力，应该合理选择磁流变阻尼器最大阻尼系数，并应限制最小阻尼系数，从而使磁流变阻尼器能发挥更好的控制效果.本算例表明，可控阻尼器最小阻尼系数可取为最大阻尼系数的1/10.

6    结论

通过上述分析，可得以下结论：

1）通过对能够同时控制结构位移、速度和加速度的主动及半主动控制策略进行研究，对Riccati微分方程进行了修正.

2）通过权重分析算例可知，主动控制中各权函数应该合理取值，才能达到较好的控制效果.选取各权重时，应考虑调整各阻尼器的能量消耗，合理确定各权重值.

3）通过半主动控制算例可知，为了获得较好的减震效果，并使磁流变阻尼器具有较大的调节能力，磁流变阻尼器阻尼系数的最大值不应过小，且阻尼器的阻尼系数最小值应该合理选择，才能达到较优的控制效果.本算例表明最小阻尼系数可取为最大阻尼系数的1/10.

参考文献

[1]     欧进萍.结构振动控制——主动、半主动和智能控制[M].北京：科学出版社，2003.

[2]     李敏霞，刘季.主动结构振动控制算法综述[J].世界地震工程，1998，14（4）：61-69.

[3]     孙清，史庆轩，张可，等.半主动变阻尼结构的振动台试验研究[J].建筑结构学报，2003，24（6）：11-17.

[4]     肖志荣，孙炳楠.斜拉索基于MR阻尼器的神经网络半主动控制[J].工程力学，2010，27（1）：183-187.

[5]     FERREIRA  F，MOUTINHO  C，CUNHA  ?，et al. Use of semi-active tuned mass dampers to control footbridges subjected to synchronous lateral excitation[J]. Journal of Sound and Vibration，2019，446：176-194.

[6]     陈超.基于MR阻尼器的结构抗震半主动控制研究[J].建筑技术开发，2013，40（3）：19-20，46.

[7]     林伟，陈尚鸿，祁皑，等.TIOC半主动控制算法在相邻结构地震响应控制上的应用[J].振动与冲击，2011，30（12）：141-146.

[8]     张志强，方自奋.基于MR阻尼器的斜拉桥半主动控制参数优化分析[J].土木工程学报，2014，47（S1）：136-141.

[9]     陈水生，刘宝龙，桂水荣.MR阻尼器对斜拉索振动控制效果的仿真分析[J].公路工程，2017，42（1）：46-51，84.

[10]   李歆，吕西林，SHIRLEY D.磁流变阻尼器的半主动控制及实时混合模拟试验研究[J].世界地震工程，2018，34（4）：130-135.

[11]   张敏.巨型减振框架结构地震反应线性最优半主动控制[J].广西工学院学报，2012，23（2）：1-6，25.

[12]   张敏，陈豆豆.设置非线性粘滞阻尼耗能框架结构地震反应分析[J].广西科技大学学报，2019，30（1）：19-30.

[13]   中华人民共和国住房和城乡建设部. 建筑抗震设计规范：GB/T 50011—2010[S]. 北京：中国建筑工业出版社，2010.