粗糙集在烤烟化学质量综合评价中的应用

褚旭，胡宗玉，王珂清，刘国庆，赵勇，张建强，邵长营，杜坚

江苏中烟工业有限责任公司，南京市建邺区梦都大街30号 210019

烟叶化学成分是烟叶品质的物质基础，与烟叶外观质量、感官质量密切相关[1]。基于烟叶的化学指标进行合理质量评价，能够真实反映烟叶的品质[2-3]，对卷烟工业企业彰显特色、定向生产具有十分重要意义。

在烤烟烟叶质量评价中，不同质量指标权的重确定方法一直是研究热点，一些新方法已被运用于权重确定领域，如主成分分析法、熵权法、综合赋权法等[4-6]。粗糙集理论是一种研究不完整、不确定知识和数据的表达、学习、归纳的数据推理方法[7]，具有不依赖先验知识而真实反映数据本身所隐藏信息的独特优势[8]。基于粗糙集理论的权重确定方法在管理决策、专家系统、机器学习和模式识别等很多领域得到成功应用[9]，但在烤烟化学质量评价中的应用目前还鲜见报道。综上，本文利用粗糙集在消除冗余信息和处理不确定信息等方面的优势[10]，通过比较粗糙集与其他决策方案的赋权及评价结果，探究粗糙集在烤烟化学质量综合评价中的应用效果，为烤烟化学质量的综合评价提供方法参考。

1 材料与方法

1.1 化学指标测定

烟叶样品取自2018年江苏中烟全国15个原料产区（分别记为1、2、3、…15原料产区），取中部（C3F）初烤烟叶样品，选择产区主栽品种，每个产区13份样品，共计195份。烤烟化学成分检测指标包括烟叶样品的总植物碱、总糖、还原糖、总氮、钾、氯6项指标，不同指标的测定方法参见文献[11]。

1.2 决策表构建

1.2.1 离散化处理

首先，通过一致化计算[10]对所选的6项烟叶化学指标的原始数据进行预处理。

（1）针对总植物碱、总糖、还原糖、总氮4项化学指标，一致化处理描述为：

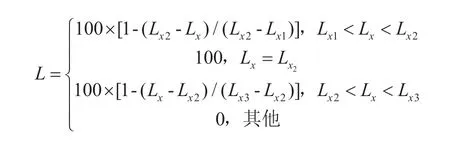
（2）针对钾指标，一致化处理描述为：

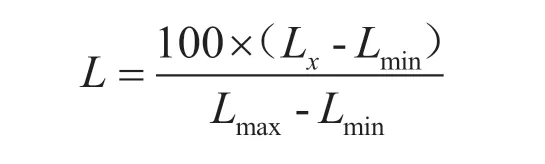
（3）针对氯指标，一致化处理描述为：

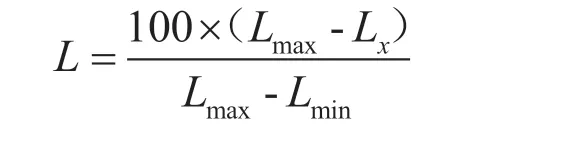
其中，Lx1为指标属性Cx下限，Lx2为属性Cx的最优值，Lx3为属性Cx的上限，Lmax为属性Cx的最大值，Lmin为属性Cx的最小值。结合相关研究成果[5,11]，确定各指标的下限、最优值及上限（表1）。

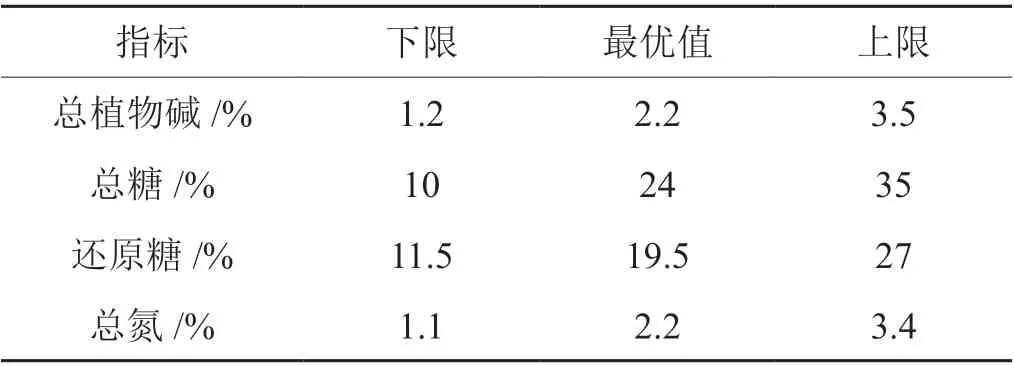
表1 烤烟化学质量指标的临界值Tab. 1 Thresholds of chemical quality indices of flue cured tobacco

由于粗糙集只能处理离散化的数据，采用等距离法[12]对一致化计算的结果进行离散化处理，具体步骤如下：

（1）指标属性Cx在离散化时的取值区间长度计算为：

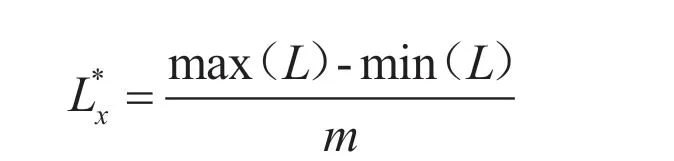
（2）对于对象Ux，其属性Cx的离散化结果描述为：

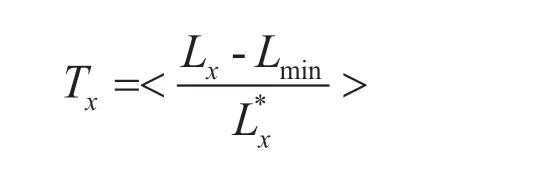
其中，Tx为对象Ux在属性Cx下的离散化结果，＜ *＞表示向上取整。

1.2.2 指标权重的初定

由于粗糙集需要处理带有决策属性集合的数据。综合国内已有研究[4,13]，选取层次分析法和标准差法分别计算单一权重，再利用基于博弈论的综合赋权法[4]对权重进行组合，得到不同烟叶化学指标的初始权重，不同烤烟化学质量指标的初始权重结果如下表：

表2 烤烟化学质量指标的初始权重Tab. 2 Initial weights of chemical quality indices of flue cured tobacco

1.2.3 决策表的构建

利用不同化学指标一致化处理得到的评分值和确定的初步权重，以加乘法原则[14]为基础，计算得到不同产区化学质量的离散化结果。最终，以6项烟叶化学指标的离散化结果为条件属性（C），以不同产区烟叶化学质量的离散化结果为决策属性（D）构建决策表（表3）。其中，C1为总植物碱，C2为总糖，C3为还原糖，C4为总氮，C5钾，C6为氯。

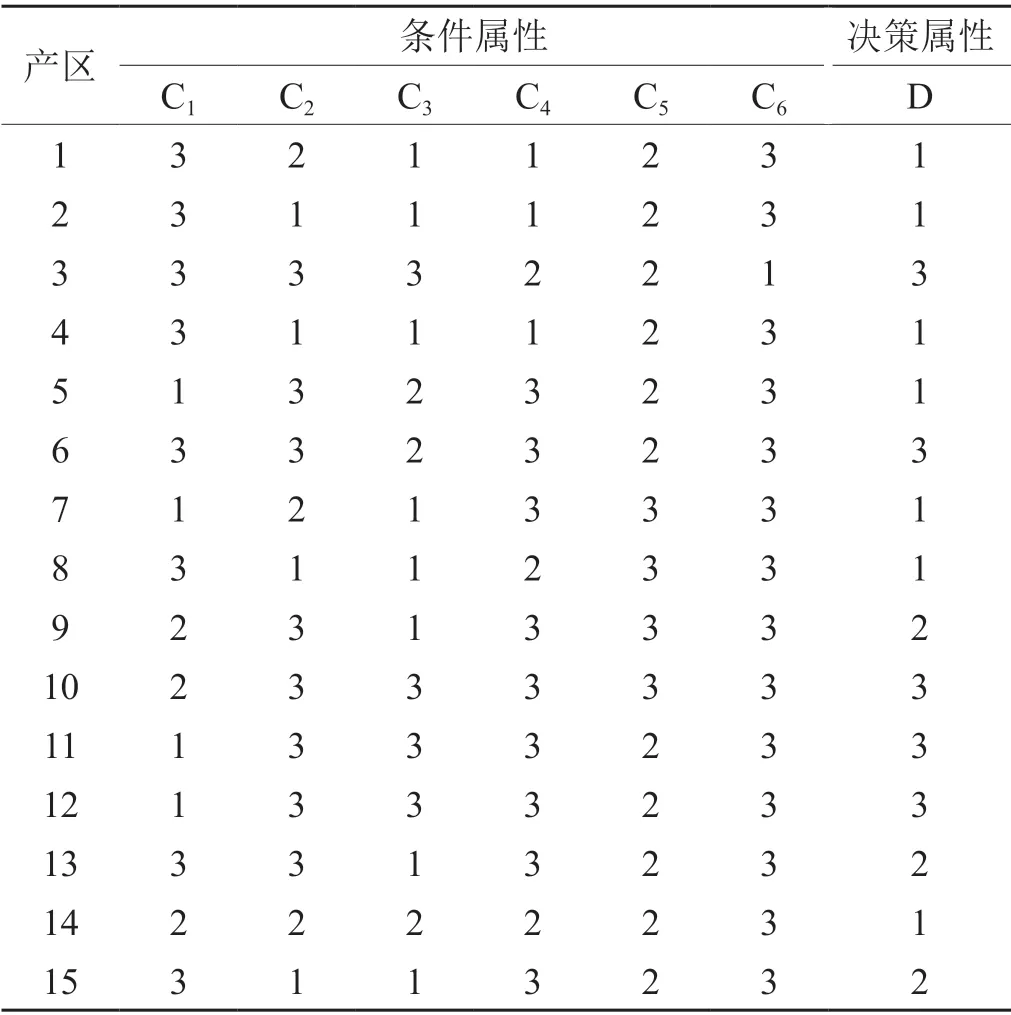
表3 烤烟化学质量评价决策表Tab. 3 Decision table for chemical quality evaluation of flue cured tobacco

1.3 基于粗糙集的权重再确定

定义S=（U，A，V，f）为一个信息系统，其中U={U1，U2，U3，…，Un}是不同评价个体的集合；A是属性的非空有限集合，C∪D=A，C为条件属性集，D为决策属性集，集合V为属性集A的值域，f是U和A的关系集，也称信息函数集[14]。若D=∅，则称信息系统S为数据表，否则称为决策信息系统或简称为决策表[7]。

1.3.1 计算等价类划分

在决策表S中，若有B⊆A，则定义属性集B上的不可分辨关系IND（B）为：

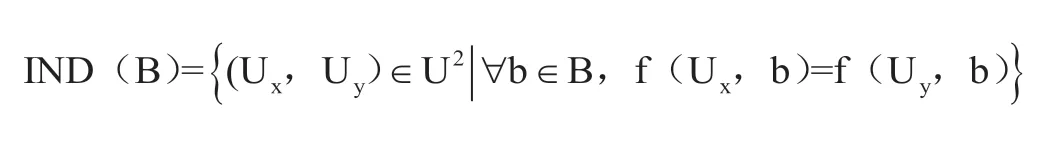
U/IND（B）称为对象集U在属性集B上的划分结果，其中的任意元素称为等价类[14]。

1.3.2 确定属性重要度

在信息系统S中，对于∀X⊆U且X≠∅，定义集合X在属性B⊆A上的下近似分级B（X）和上近似划分及B（X）为：

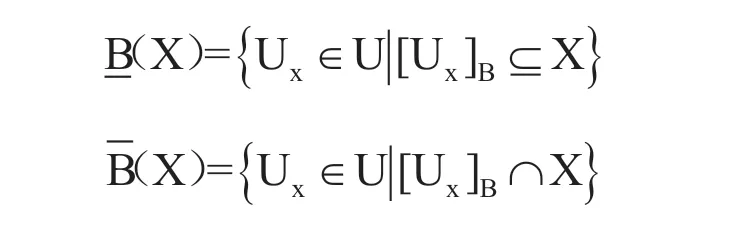
其中，[Ux]B= { Uy|（Ux，Uy）∈IND（B）}，B（X）也称为X的B正域[10]，记作：POSB（X）。

对决策信息系统而言，每个条件属性的重要程度不同，粗糙集采取的是先去掉一个属性，再考虑没有该属性后等价类划分变化情况的思想[9]。若去掉的属性对后续分类变化的影响比较大，则该属性的强度大，重要度高，否则该属性的强度小，重要度低。根据这一特性，定义决策属性D对条件属性C的依赖度为：

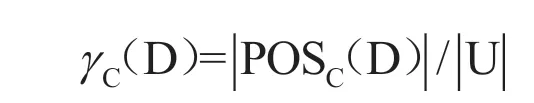
依据条件属性的依赖度，条件属性Cx⊆C的重要度定义为：

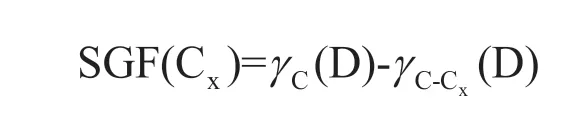
上述粗糙集理论中所有的概念和运算均基于代数的等价关系和集合运算定义，一般称为粗糙集的代数表示。由于粗糙集的代数表示法直观性较差[7]。进一步的，建立粗糙集与信息熵的关系，从信息的角度对粗糙集的概念与运算进行表达，称为粗糙集的信息表示。

在决策表S中，若有U/IND（C）={ C1，C2，C3，…，Cm}，U/IND（D）={ D1，D2，D3，…，Dk}，则定义决策属性集D相对于条件属性集C的条件信息熵[7]为：

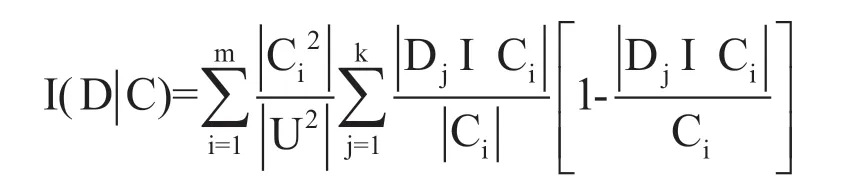
条件属性集的信息熵具有单调下降的性质[7]，故对于∀Cx∊C，定义属性Cx在粗糙集信息表示下的重要度为：

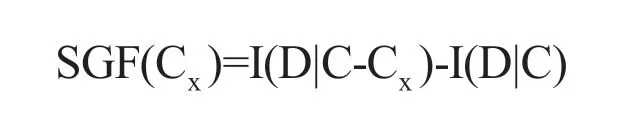
综合粗糙集的代数表示法和信息表示法，条件属性Cx的重要度SGF（Cx）越大，则指标越重要，该属性的权重也越大。由此，属性Cx的权重为：

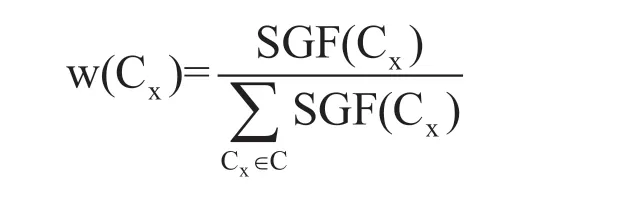
1.4 决策方案的比较

1.4.1 区分度计算

为进一步验证不同决策方案的合理性和优越性，通过计算区分度[10]对不同决策方案进行对比分析，

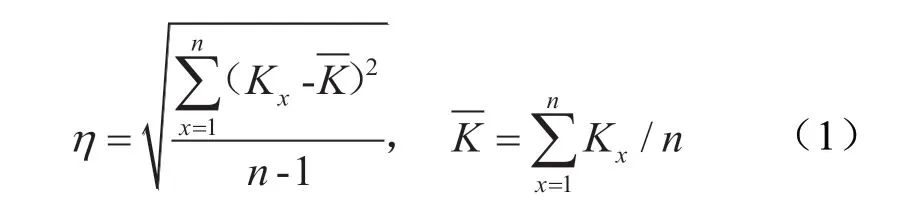
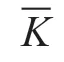
1.4.2 收敛性分析

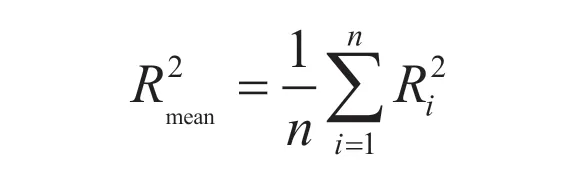
1.4.3 相关性分析

采用斯皮尔曼（Spearman）等级相关系数计算不同决策方案评价结果间的密切程度[13]。

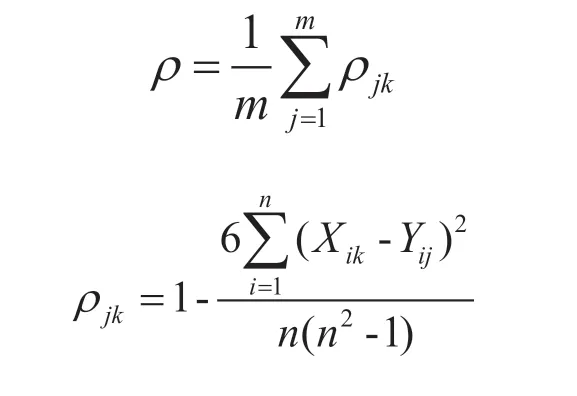
式中，ρjk为不同决策方案间的等级相关系数，反映不同方法间的相关程度，ρjk越大表示两种方法所得评价结果的相关程度越高，ρ为平均相关程度。Xik和Yij分别表示第i个评价对象在第k种和第j种决策方案下的排序值。

1.5 数据处理

由于不同化学质量指标量纲不同，涉及标准化的过程利用式（2）进行处理。式中，D为烤烟化学指标属性的归一化值，D0为属性的原始值，Dmin为属性最小值，Dmax为属性最大值。

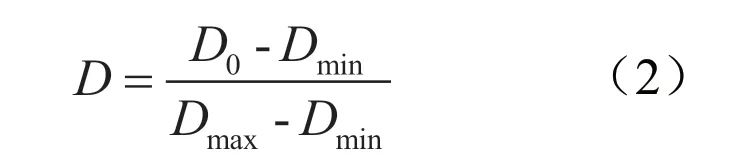
应用Matlab 2009b编程进行数据分析，SPSS 18.0和EXCEL软件进行统计分析做表。不同产区烟叶样品的各项指标属性在计算所有样品的基础上汇总平均得到。

2 结果与分析

2.1 烤烟化学指标的描述性统计

烟叶6项化学指标的描述性统计结果见表4。与优质烟叶化学指标[11]的标准相比，不同产区烟叶总植物碱、总氮、钾含量和氯含量的平均含量较适宜，总糖、还原糖的含量均值较高。从不同化学质量指标的变异幅度可以看出，变异最小的为烟叶的总糖、还原糖和总氮3项指标，变异系数均为0.18。变异幅度最大的是烟叶的氯含量，变异系数0.72。

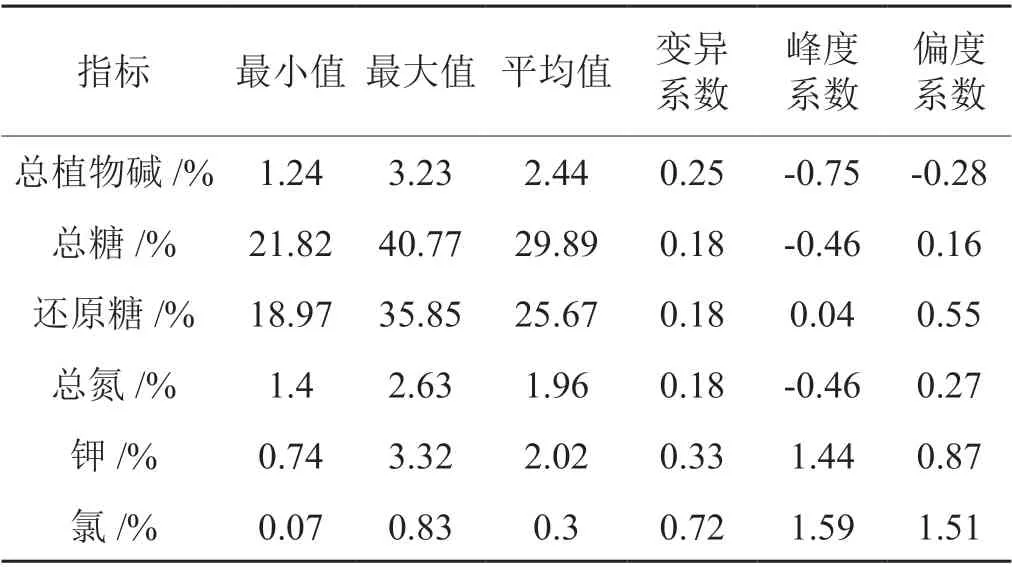
表4 烤烟化学质量指标的描述性统计Tab.4 Descriptive statistics of chemical quality indices of flue cured tobacco

从不同化学质量指标数据的分布情况来看，烤烟烟叶的总植物碱、总糖、总氮3项指标曲线偏平阔，还原糖、钾、氯3项指标的曲线偏尖削。偏度系数的分析结果则表明，除了烟叶的总植物碱的数据分布曲线呈现左偏外，其余5项指标的数据的分布曲线均呈现右偏型。

2.2 等价类划分及指标权重的再确定

对表3中的数据论域分别按条件属性和决策属性进行等价类划分：

依次去掉一个条件属性后的论域等价类划分为：

各条件属性的依赖度为：

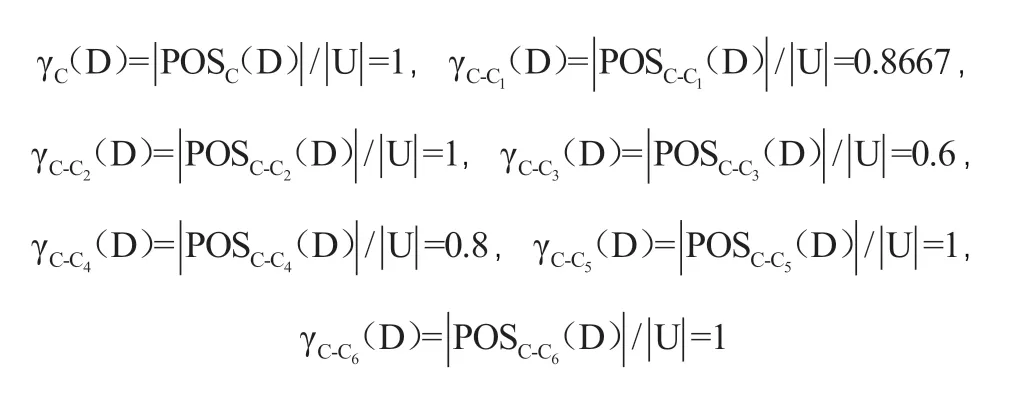
各条件属性的信息熵为：

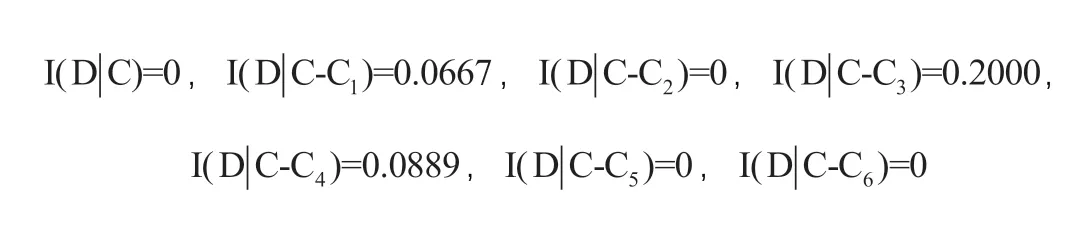
上述各条件属性依赖度和信息熵的计算结果，经归一化处理后分别得到粗糙集代数表示法和信息表示法的属性重要度，最终确定不同条件属性即烤烟化学质量指标的权重系数（表5）。由表可见，在层次分析法的赋权结果中，主观因素占主导地位，权重系数最大的是总植物碱指标，权重系数为0.286，赋权结果最小的指标为总糖和钾，权重系数均为0.125；标准差法的赋权结果较为平均，权重系数最大的指标是总植物碱和总氮，均为0.18，总糖、还原糖、钾和氯4者的指标权重均为0.16；基于博弈论的综合赋权法则是将前两者的权重结果综合起来，即极小化可能的权重与各基本权重间的偏差[4]，赋权结果更趋一致，其赋权系数最大的是总植物碱指标，为0.277，最小的指标是总糖和钾，为0.128；基于粗糙集的代数表示法和信息表示法的赋权结果中，权重系数最大的均为还原糖指标，分别为0.545和0.562，最小的均为总植物碱指标，权重系数分别为0.182和0.188。

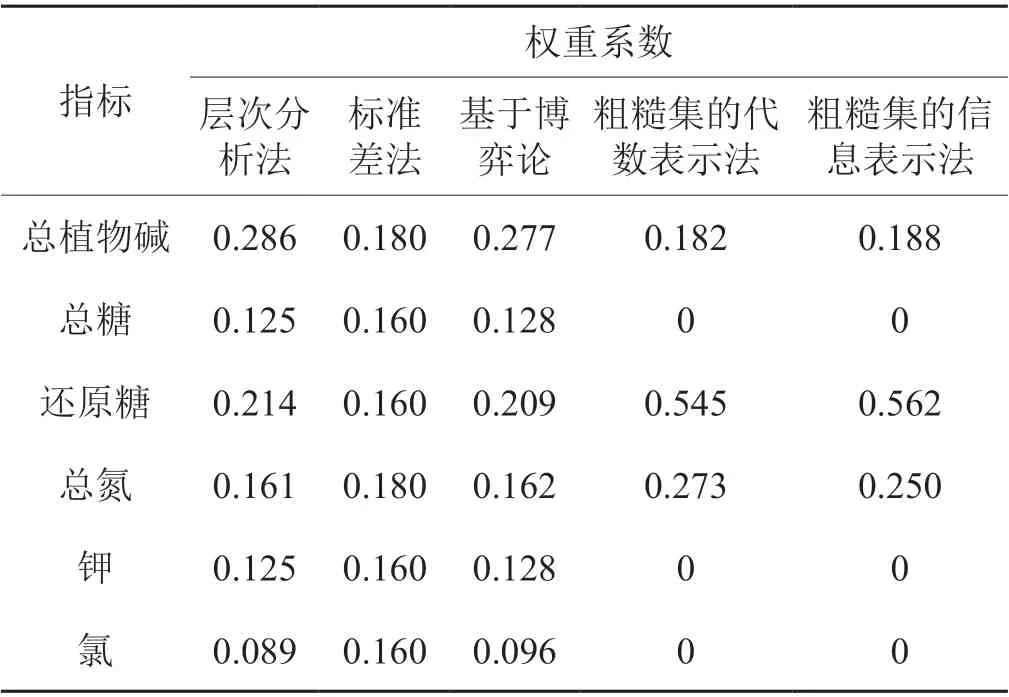
表5 不同决策方案的权重结果Tab. 5 Weight results of different decision schemes

与前3种评价方法相比，基于粗糙集理论计算的赋权结果更趋一致，均提高了还原糖和总氮的指标权重，总植物碱指标的权重较层次分析法和基于博弈论的综合赋权法则有所下降。同时，粗糙集的代数表示法和信息表示法计算的总糖、钾和氯3项指标的属性的重要度为0，未分配权重系数，确定为冗余属性[15]。分析发现，粗糙集代数表示法和信息表示法的赋权结果将权重主要集中于还原糖、总氮和总植物碱3项指标，一方面与指标数据本身的分布特征相关。从不同指标数据分布的特征及化学质量决策表中的分级档次发现，不同产区烟叶的钾、氯含量的数据分布较为集中，其中指标钾的分级档次除产区7-10为3（好）外，其余均为2（中等），指标氯的分级档次除产区3为1（差）外，其余均为3（好）。另一方面，从粗糙集中属性重要度的定义也可以看出，总糖、钾和氯3项指标的有无对后续等价类划分的结果没有影响。而还原糖、总氮和总植物碱3项指标的影响较大，其中又以还原糖的强度最大，重要性最高。参考前人研究发现[16-17]，与国外主流烟叶相比，我国主要产区烟叶普遍呈现出总糖含量较高，而氯含量较低等特点。同时，烤烟烟叶的总氮、总植物碱含量与感官质量呈现显著相关关系，还原糖含量对于改善烟叶化学质量，提高烤烟吃味品质起关键作用[18-19]。相对来说，还原糖、总氮和总植物碱3项指标对烟叶质量的影响更大。

2.3 不同产区烤烟化学质量的综合状况

进一步的，利用层次分析法、标准差法和基于博弈论的综合赋权法评价的不同产区烤烟化学质量的综合状况如表6所示。由表可见，层次分析法中化学质量评价最高的是产区10，得分为71.59，最低的是产区7，得分37.72，综合排名情况为（13，14，3，10，12，2，15，9，8，1，5，4，6，11，7）。基于标准差法计算的烤烟化学质量的综合得分最高的是产区10，得分74.4，最低的是产区1，得分40.7，综合排名为（15，14，4，13，8，5，12，10，6，1，2，3，7，11，9）。基于博弈论的综合赋权法计算的综合评价结果最高值为71.84，为产区10，最低值为38.42，为产区7，排名情况依次为（13，14，3，12，10，2，15，9，8，1，5，4，6，11，7）。

进一步的，在粗糙集的代数表示法和信息表示法确定的不同产区烤烟化学质量的综合排名中（表6），粗糙的代数表示法计算得到的评价最高值为产区12，分值为82.42，最低值为产区4，分值为23.34，排 名 的 依 次 为（13，14，3，15，7，5，12，11，10，4，2，1，6，9，8）。粗糙集的信息表示法计算得到的最高值82.01，为产区12，最低值为22.8，为产区2。排名的依次为（14，15，3，13，7，5，12，11，10，4，2，1，6，9，8）。

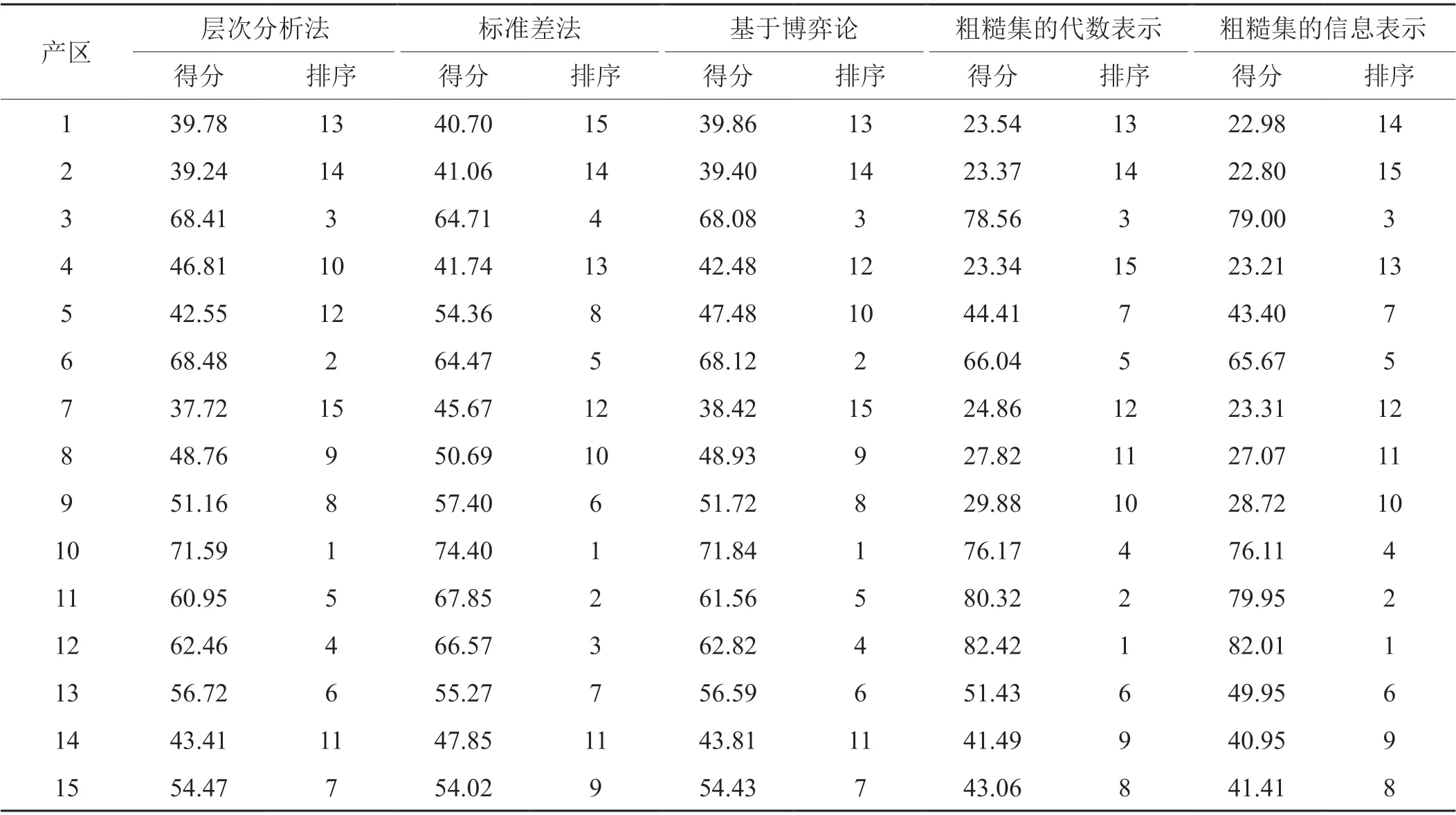
表6 不同评价方法的得分结果Tab. 6 Results of different evaluation methods

2.4 不同决策方案的比较

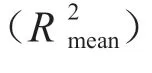
不同评价方法的区分度分别用η1（层次分析法），η2（标准差法），η3（基于博弈论的综合赋权法），η4（粗糙集的代数表示），η5（粗糙集的信息表示）表示，借助公式（1）计算得出，η2（10.68）＜η3（11.36）＜η1（11.49）＜η4（23.07）＜η5（23.36），借助粗糙集代数表示和信息表示计算得出的η显著高于其他决策方法，其中又以粗糙集的信息表示法的区分度最大，可分辨性最高。

最后，计算不同决策方案评价结果间等级相关系数（表7），层次分析法、标准差法及基于博弈论的综合赋权法分别用r1，r2及r3表示，粗糙集的代数表示法和信息表示法分别用R1和R2表示。从表中可以看出，不同决策方案间密切程度的排序结果依次为：粗糙集的信息表示法（0.934）＞基于博弈论的综合赋权法（0.931）＞标准差法（0.928）＞粗糙集的代数表示法（0.927）＞层次分析法（0.924）。相关系数均值最高的是粗糙集的信息表示法，最低的是层次分析法。由此可见，基于粗糙集的代数表示法和信息表示法的区分度高于其他3种决策方法，收敛性更好，而其中又以粗糙集的信息表示法与其他方法的密切程度最好，一致性最佳。

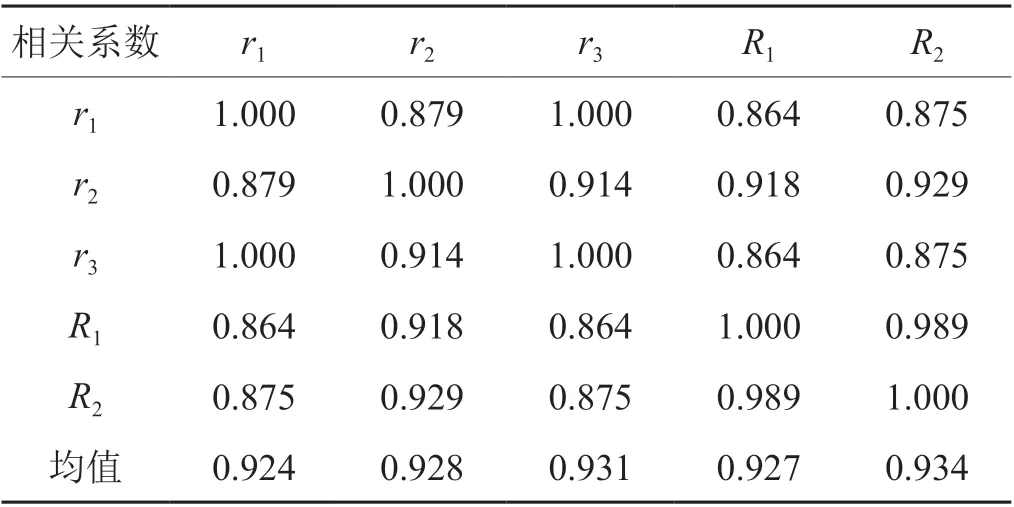
表7 等级相关系数矩阵Tab. 7 Rank correlation coefficient matrix

3 结论与讨论

烤烟化学质量的综合评价是一个无决策属性的多指标属性决策过程，解决不同指标属性权重的分配问题是一个重要的前提。目前，确定指标权重的方法主要有主观赋权法和客观赋权法。其中，主观赋权法需要大量的先验知识[20]，评价结果具有一定的主观随意性，较少考虑评价指标之间的依赖关系，应用过程中有很大的局限性。客观赋权法则是根据不同指标属性值的差异大小确定指标权重，差异越大权重越大，反之则越小[4]。

本文利用粗糙集理论在消除冗余信息和处理不确定性信息等方面的优势进行烤烟化学质量的综合评价。借助粗糙集的代数表示法和信息表示法，通过构建决策表、计算等价类划分和属性重要度，确定烟叶不同化学质量指标的权重系数，并最终计算不同产区烟叶化学质量的综合评价得分和排名。对比不同决策方案的权重结果发现，不同评价方法的赋权结果不尽相同，依据粗糙集理论计算的指标属性权重更趋一致。其中，层次分析法以主观因素占主导地位，标准差法的权重结果更趋平均，基于博弈论的综合赋权法则综合了前两者的权重结果，极小化基本权重系数间的差异[4]。基于粗糙集的代数表示法和信息表示法将总糖、钾和氯3项指标定义为冗余属性，将指标权重主要集中于还原糖、总氮和植物碱3项指标，其中又以还原糖的属性重要度最高，指标权重最大。基于粗糙集的代数表示法和信息表示法充分考虑了各属性指标的分布特征和专家经验，克服了层次分析法赋权过程中存在的主观随意性。

比较不同决策方案的得分最高、最低值以及排序情况发现，计算得出的结果不尽相同。进一步地，通过进行区分度计算、相关性和收敛性分析比较不同决策方案的评价结果，基于粗糙集理论计算的评价结论的区分度普遍较高，收敛性更好。通过计算不同决策方案评价结果间的密切程度发现，基于粗糙集的信息表示法与其他评价结论的相关性程度最高，一致性最佳，能够较好地区分不同产区烤烟化学的综合质量，适合于烤烟化学质量的综合评价。

通过对烤烟化学质量的综合状况进行评价，可以充分了解不同烟区烟叶化学成分的特点，对于指导烤烟生产起着重要作用，而且对于卷烟工业企业充分利用烟叶原料也有着极其重要的意义[2,19]。

值得注意的是，基于粗糙集理论的指标赋权方法是一种客观赋权法，依赖的是取样数据本身的差异。同时，在确定决策属性时，由于不同产区不同的气候环境、烟叶栽培管理措施和品种遗传特性，造成了不同产区和品种间较大的差异和个性化的存在[21]，为了更加合理评价不同产区、品种和香型烟叶的化学综合质量，部分化学指标适宜值的选取需结合已有研究和使用需求，针对性地设定评价参数，并进一步深入研究。