包角对高比转速双叶片自吸离心泵外特性及振动特性的影响

2021-09-26裘孙洋潘金豪

流体机械 2021年8期

关键词：扬程离心泵脉动

裘孙洋，潘金豪

（1.浙江大学化工机械研究所，杭州 310027；2.杭州中能汽轮动力有限公司，杭州 310018）

符号说明：

ρ——密度，kg/m3；

k——湍动能，m2/s2；

u——速度，m/s；

ω——单位时间耗散率，s-1；

τij——湍流剪应力，Pa；

μ——动态黏度，kg/（m·s）；

γ——k- ω模型函数；

nq——比转速；

KS——泵壁粗糙度，mm；

Qm——质量流速，kg/s；

H——扬程，mm；

P——压力，Pa；

N——每转样本数；

σp——压力标准偏差，Pa；

ϕ——叶片包角，（°）；

t——时间，s；

Sij——无量纲应变张量；

Φ1，Φ2——k-ω湍流模型和k-ε湍流模型中的常数；

F1，F2——混合函数；

y——离最近的壁面的距离，m；

ν——流体运动黏度，m2/s；

N——无量纲常数，N=60；

Pri——i号监测点压力值，Pa；

Prav——监测点一个周期内压力平均值，Pa。

0 引言

随着城市化进程的不断加深，排污泵在城市污水处理，市政工程，自来水厂给水中的应用越来越广泛。一般情况下，为了避免污水中的固体悬浮物堵塞排污泵，其叶轮采用无堵塞设计方法，叶片数较少，但是包角较大［1-2］。同时，由于污水泵流量较大，扬程要求不高，所以形成了其叶轮宽度较宽，直径较小的结构。在不恰当的包角角度下，该结构容易在运行过程中引起回流及压力脉动，造成排污泵性能降低，引发强烈的振动和噪声［3-4］。黄茜等［5］研究了叶片包角对高比转速离心泵性能的影响，叶片包角的大小对高比转速离心泵扬程、效率及最佳工况点都具有明显的影响，同时，对于振动噪声存在一个最佳包角角度使得动静干涉作用最小。王勇等［6］研究了离心泵叶片包角对离心泵流动诱导振动噪声的影响，采用实验的方法在离心泵闭式试验台上采集了不同包角情况下的离心泵振动和噪声信号。在各个流量工况下，随着叶片包角的增加，模型泵噪声信号的轴频峰值呈现先增加后减小的趋势，为低噪声离心泵水力的优化设计提供参考。郎涛等［7］进行了双叶片污水泵内部流场的PIV试验，分析了各个流量工况下的叶轮内部流场相对速度分布，引入少叶片数离心泵内部流动理论，揭示了流场内部轴向漩涡和低速区随流量变化的形态特征及发展的内在机理。朱荣生等［8］对双叶片泵内的压力脉动进行了分析，确定了压力脉动与泵内动静耦合之间的关系，小流量情况下压力脉动幅值更大，设计工况下压力脉动最小。

鉴于节能减排的生产实际要求，提高高功率大流量污水泵效率对于减少能源消耗具有重要意义，目前的高比转速离心泵并不能满足高效率指标这一要求。同时，国内外之前的研究中采用的样本数量较小，并不具有较为可靠的规律性的结论，本文在前人研究的基础上，对双叶片情况下叶轮包角角度大小进行研究，从而得出具有普适性的结论，指导设计高效的双叶片叶轮。

1 数值模拟

1.1 模型建立

以300zw800-15无堵塞自吸式污水泵为研究对象，其叶轮结构如图1（a）所示。为了研究包角对双叶片叶轮的影响，在不改变叶轮其他设计参数的情况下，对叶片包角进行了从230°～300°的改型，具体改型样式如图1（b）所示。

图1 自吸泵叶轮及改型模型Fig.1 Self-priming pump impeller and modified model

图2 自吸泵流体域及网格模型Fig.2 Self-priming pump fluid domain and mesh model

该泵采用的是高比转速的叶轮，为了达到较高的运行效率，所以其出口边为斜边。同时为了使得数值模拟得到与实际运行工况最为相似的结果，在叶轮进口前加装一段进水弯管。该泵的具体设计参数为：设计流量Q=800 m3/h，设计扬程H=15 m，转速 n=1 480 r/min，叶片数 Z=2，进口直径D1=250 mm，出口直径D2=290 mm，叶轮出口宽度b2=192 mm。

1.2 湍流模型

随着计算流体力学技术的发展，离心泵数值模拟方法已经广泛应用于离心泵设计过程中，且具有良好的准确性［9-13］。本文在数值模拟过程中采用描述三维不可压缩黏性流体的N-S方程作为控制方程［14-17］，湍流模型采用SST k-ω湍流模型［18］，其优点在于近壁面的计算相较传统的k-ε模型更为准确［19-20］，其具体形式为：

τij的计算式为：

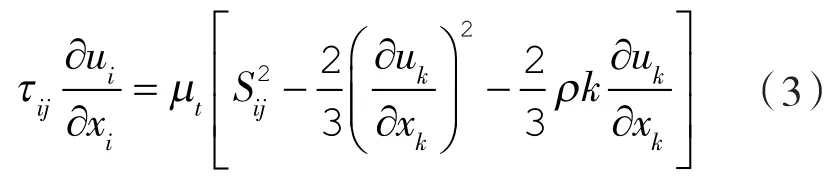
定义混合函数为：

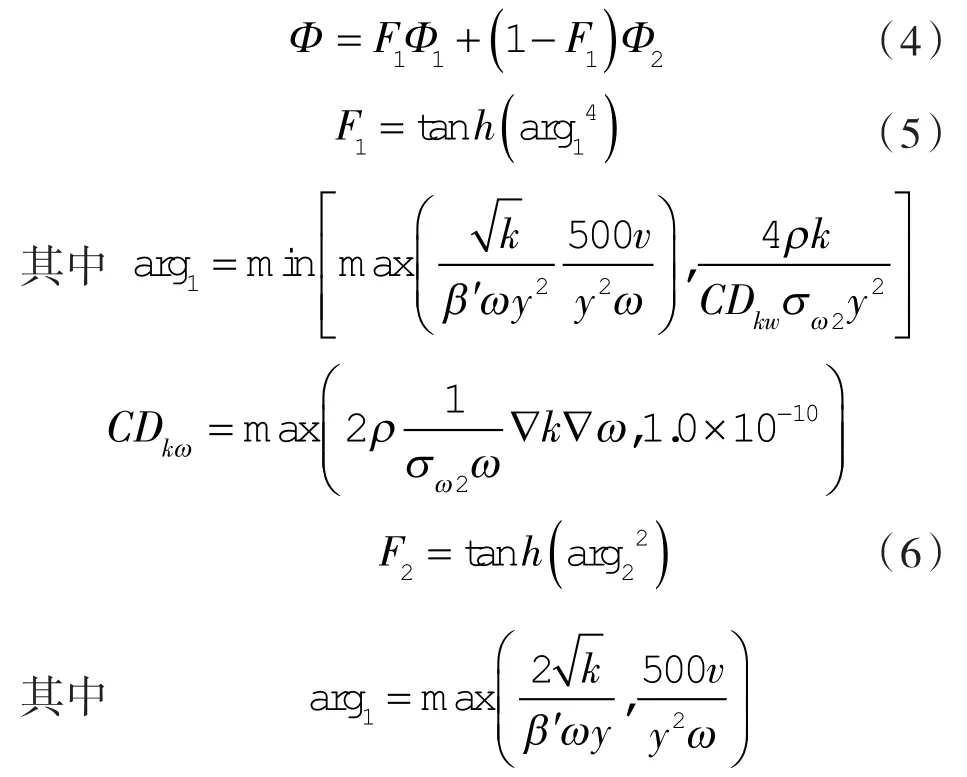
上文式中未解释字母皆为无量纲系数，β'=0.09，α1=5/9，β1=0.075，σk1=2，σω1=2，α2=0.44，β2=0.082 8，σk2=1，σω2=0.856［21］。

1.3 网格划分及边界条件设置

本文采用ICEM软件进行网格划分，采用CFX软件进行流体域的数值模拟计算。由于研究模型结构较为复杂，为了得到最佳的数值模拟效果，对离心泵模型整体采用非结构化网格进行划分，同时在必要的流体区域进行网格加密。通常来说流体域中叶轮与蜗壳的网格数量较多，进水延长管、出水延长管及进水弯管的网格数量较少，以便控制网格数量的同时得到较好的网格整体质量。网格无关性分析方案见表1。对整个流体域网格进行网格无关性分析，选取5组不同网格数量的模型在设计工况下进行定常计算，在叶轮网格数达到80万，蜗壳网格达到60万后扬程变化小于1%。因此保证各个模型叶轮网格数量最终在85万左右，蜗壳网格数量在65万左右，整体网格数量在180～200万之间［22］。采用多旋转坐标系法处理叶轮的旋转，壁面粗糙度KS=0.04 mm，质量流量入口Qm=222.2 kg/s，自由出流［23-25］。

表1 网格无关性分析Tab.1 Grid independence analysis

1.4 非定常模拟及监测点设置

非定常计算监测点分布如图3所示，每隔30°取一个监测点（P1，…，P12）。总共计算 6个叶轮旋转周期，总时间为0.243 243 s，叶轮选择每3°作为一个时间步长，为 3.378 4×10-4s，每个时间步长迭代20次，取最后一个周期，即最后120个时间步长用以分析压力脉动情况。

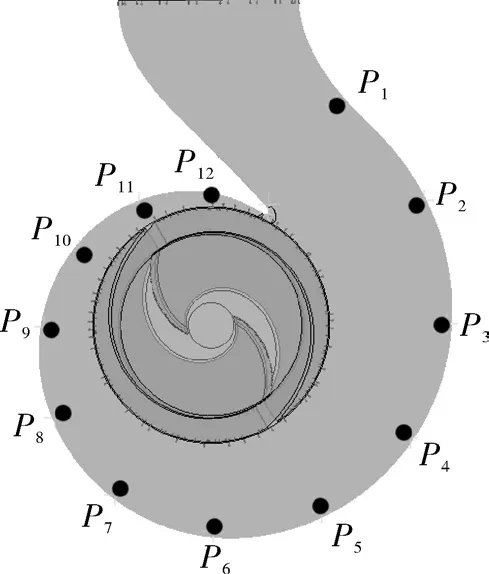
图3 监测点分布Fig.3 Distribution of monitoring points

2 外特性和脉动特性分析

2.1 试验装置与数值模拟结果

依据GB/T 3216-2005《回转动力泵水力性能验收试验1级和2级》对该泵进行外特性试验。试验台示意如图4所示。

图4 水泵试验台示意Fig.4 Sketch of pump test rig

试验流量范围为18.70～188.82 L/s，取其中部分数值用作分析。试验中使用的流量计为利欧泵业有限公司测试中心编号LEO-200s-10-00_0_300的电磁流量计。试验电机效率为95.6%，电机实际功率通过高压宽带功率分析仪得到，再通过计算转换成离心泵扭矩。其他主要试验设备还包括手持式转速仪和进出口压力变送器。开启试验泵后先暖泵30 min再测量各个参数数据。由进出口压力变送器可以算出试验扬程；由高压宽带功率分析仪和手持式转速仪可以得到离心泵输入功率，两者相除得到试验效率。

图5示出300zw800-15模型泵数值模拟扬程预测值与试验扬程的对比。从图中可以看出，模型泵数值模拟结果和试验结果在趋势上保持良好的一致性。数值模拟的扬程在各个流量工况点上相较于试验结果偏高，这可能是由于试验泵的壁面粗糙度过大造成的。从整体上来说，数值模拟结合和试验结果的误差不超过5%，在设计工况点下3%，数值模拟结果具有良好的可信度。

图5 扬程预测值与试验扬程的对比Fig.5 Comparison diagram of predicted head and tested head

2.2 各个模型外特性分析

通过试验，可以得到模型在各个流量工况下的外特性性能曲线，图6示出了不同包角角度下在0.8Q（小流量工况），1.0Q（设计工况）和1.2Q（大流量工况）时的流量-扬程曲线，流量-转矩曲线和流量-效率曲线。

图6 各模型性能曲线Fig.6 Model performance curves

从图6中可以看出，在设计工况下，随着包角变大，该泵的扬程有一定程度上的先上升后下降的过程，在大流量工况下扬程随着包角增大下降的幅度更明显，在小流量工况下扬程下降的较少。其原因为在包角过小的情况下，该叶轮中存在着严重的湍流及回流情况，严重影响了流道的流体通过能力，造成扬程的极大下降。小流量工况下叶轮流道中也存在着严重的湍流情况，包角的增大对于改善湍流有一定的作用。在包角大于250°之后，继续增大包角会导致扬程的略微下降，同时观察扭矩变化规律可发现，随着包角的增大，叶轮扭矩不断减小，这是由于随着包角增大，流体流道变长，其安放角分布逐渐变得平缓，观察速度三角形可以发现叶片对流体做功减少，从而使得扬程及叶轮扭矩皆降低。在设计工况点，随着叶片包角的增大，叶轮效率先快速上升，在280°时达到最大效率点，然后再缓慢下降，存在着一个最佳包角角度使得叶轮的效率在设计工况点达到最大。在小流量工况下本文所模拟的污水泵叶轮效率随着叶片包角的增大不断增大，尚未达到最大值，同时在大流量工况下叶轮在包角为240°时达到效率最大值。在离心泵叶轮的设计过程中，包角的增大还会引起铸造难度的增大，所以在设计产品中要综合考虑性能和制造难度来选择叶轮包角。

2.3 蜗壳内压力脉动情况分析

定义压力脉动标准差σp为：

2.4 叶轮包角对离心泵压力脉动的影响

通过对各个不同包角设计工况下的非定常计算，得到如图7所示的各个包角情况下不同监测点的压力脉动标准差分布。由图中可以看出，位于隔舌附近的监测点P2，P3处压力脉动最大，同时隔舌正对面位置的监测点P8，P9处压力脉动较为次之。且在总体上来说，包角越大，监测点的压力脉动越大，当包角从280°～300°时P2处的压力脉动上升较多，包角从230°～280°压力脉动变化较小。

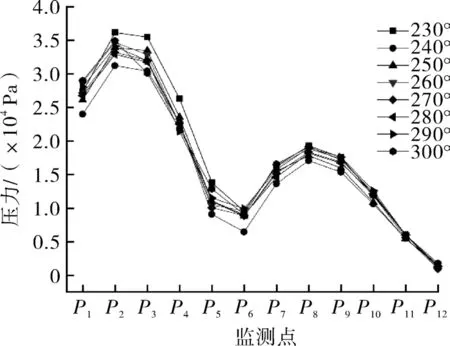
图7 原模型周向压力脉动曲线Fig.7 Circumferential pressure pulsation curve in original model

3 流动状态分析

3.1 叶片包角对污水泵内流场的影响

图8示出各个不同包角角度下离心泵叶轮叶片扫过隔舌时的速度矢量。

图8 不同包角下速度矢量Fig.8 Velocity vector diagram under different wrap angles

离心泵内所产生的压力脉动及振动，主要可以归结于叶轮尾迹流与隔舌的干涉。当包角角度较小时，叶片尾迹流较为集中，速度衰减较快，通过隔舌的时候，其高速区通常集中在叶片尾部（230°）。随着包角的增大，由于流体流动更加贴合叶片的形状，其尾迹流会有一定程度的延长，速度衰减减缓，在通过隔舌后，整个叶片表面的速度分布较为均匀（260°）。当叶片包角继续增大的时候，流体尾迹逐渐向叶轮头部延展，形成从叶片头部一直到叶片尾部的高速尾迹区，当通过隔舌时，叶片尾部的尾迹消散，使得叶片上流体的高速区主要集中在叶片头部（300°）

图9示出包角为270°的叶轮旋转180°时各个旋转角度的离心泵内压力变化情况，每20°保存一次压力分布云图。从图9中可以看出，在各个叶轮相位下叶轮中心的压力都是最低的，随着叶轮相位的变化，双叶片离心泵内的压力分布变化较为剧烈。当叶片扫过隔舌的时候，整体截面的压力均值较高，当叶片原离隔舌的时候整体截面的压力分布较低。

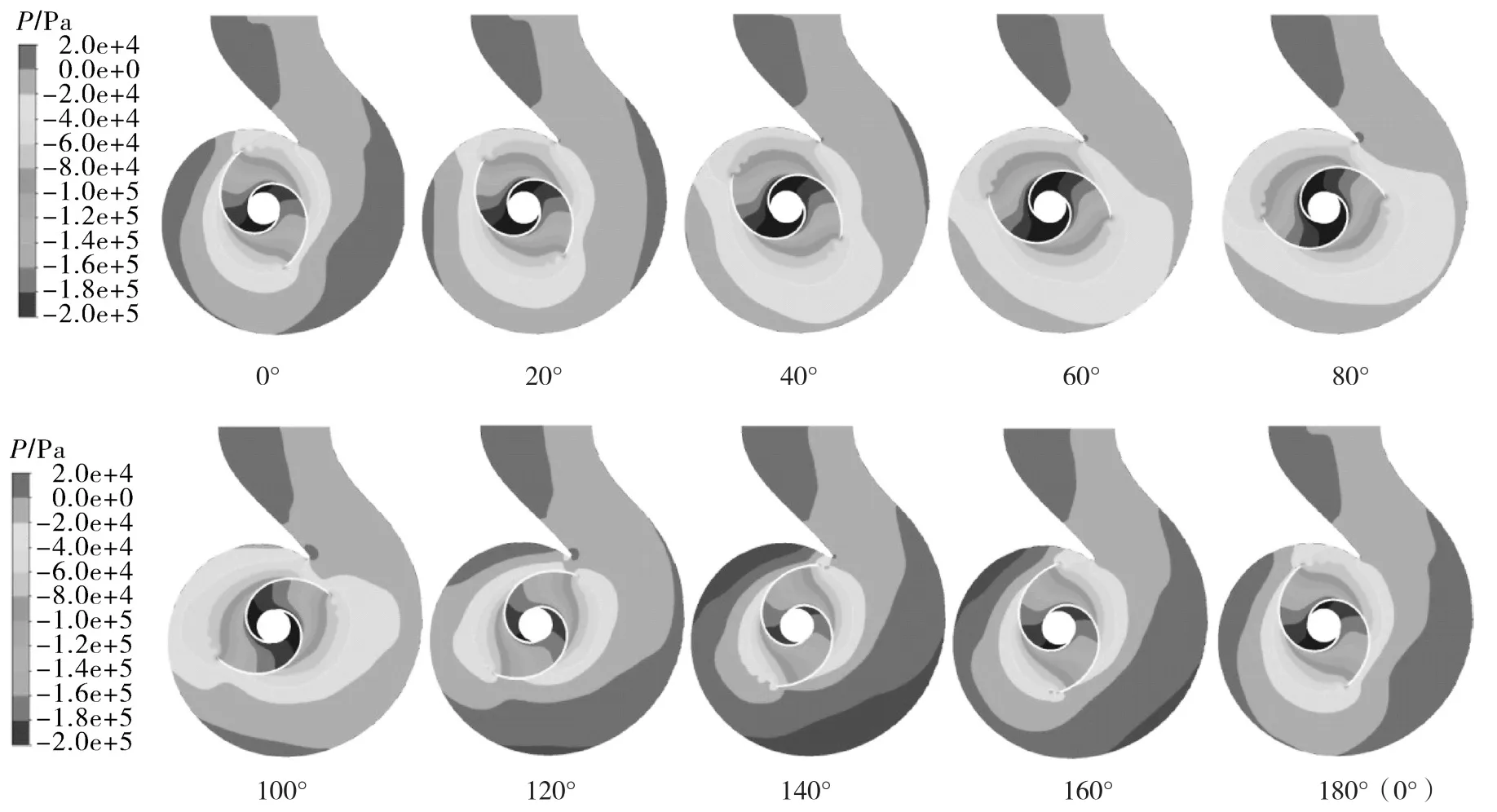
图9 不同时刻压力云图Fig.9 Pressure nephograms at different blade phases

图10示出各个不同包角情况下离心泵内湍流黏度情况的分布云图。湍流黏度是表征当流体处于湍流状态时，由于随机脉动造成的强烈涡团扩散导致的流体黏性增大现象。

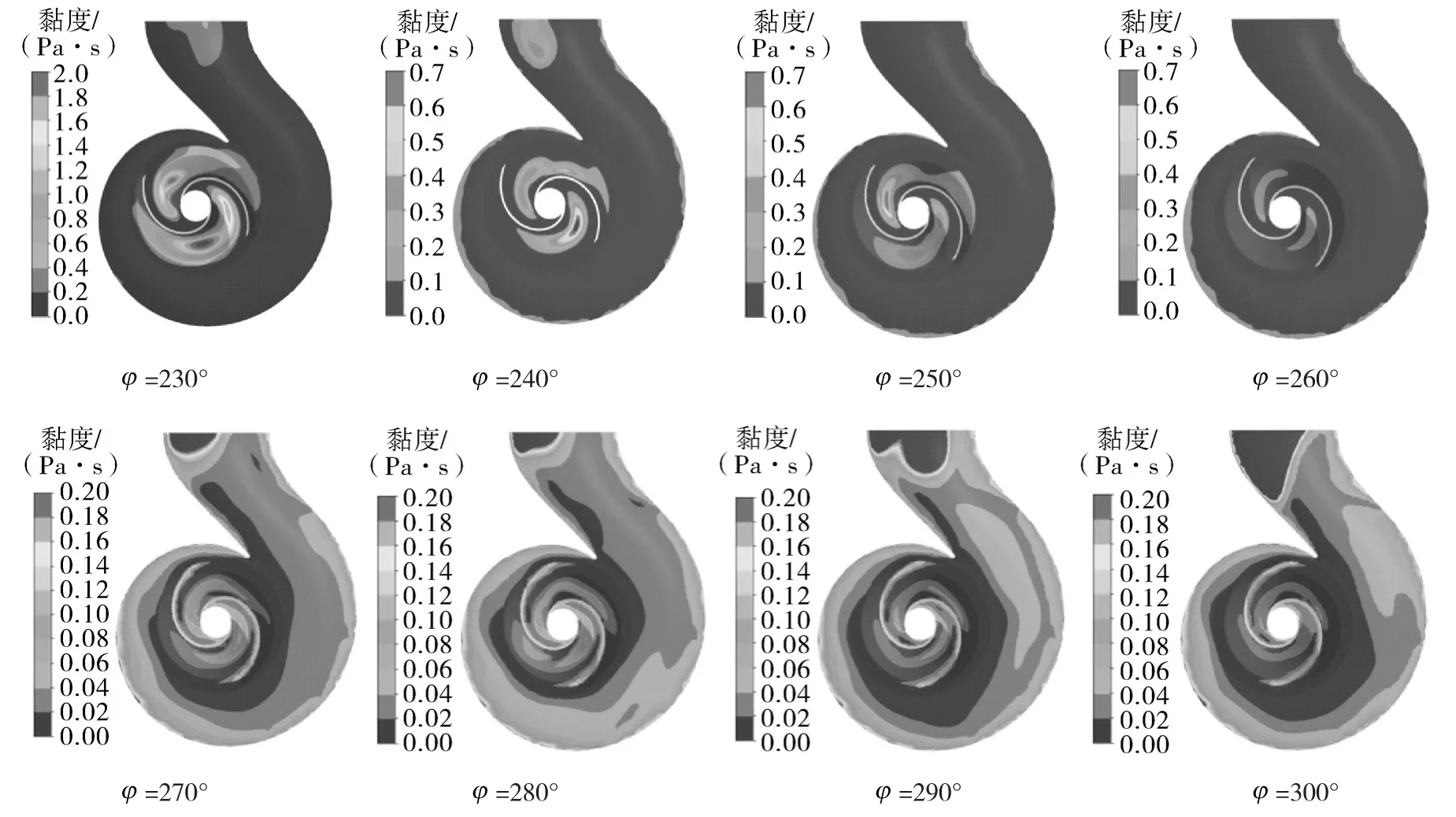
图10 不同包角下离心泵内湍流黏度分布云图Fig.10 Turbulent viscosity distribution nephograms under different wrap angles

当包角角度较小时，流道内的湍流黏度较大，且最大黏度发生在叶片前1/3位置附近。同时，由于隔舌的干涉现象，会导致靠近隔舌的一侧湍流黏度更小，远离隔舌的流道湍流黏度更大。这说明隔舌一定程度上阻挡了相近流道中的湍流扩散情况，使得漩涡减小，湍流黏度降低。随着包角的增大，其内部的湍流黏度值不断减小，最终会使得流道中的湍流黏度比壁面摩擦导致的湍流黏度还要低，使得流道中的湍流黏度属于次要干扰。当包角增大到一定程度，湍流黏度的干扰变为次要因素之后，包角的进一步增大不会使得流场中的阻力因素继续降低，反而会增大壁面面积，增大了壁面导致的漩涡和湍流干扰。不同包角的不同湍流黏度揭示了较小包角情况下是流体容易产生湍流和流动分离漩涡导致了对流体产生阻碍，从而使得整体的效率下降。同时，随着包角的增大，流道中的湍流黏度变成次要干扰，这时主要的效率下降因素变为壁面粗糙度及壁面面积，所以过大的包角会使得壁面损失增大从而降低离心泵的整体效率。