给水泵扬程曲线斜率的研究实践
2022-06-23徐秀生王玉霞
文/徐秀生 王玉霞
超(超)临界锅炉给水泵减小扬程曲线斜率系数K值的研究实践——当前,火电、核电用泵和以绿色能源为动力的太阳能泵及风能泵等,为了保证能够稳定运行,对于降低泵关闭点功率以及关闭点扬程对给水泵管路系统的影响等问题,用户和设计院通常对给水泵性能曲线的形状以及关闭点扬程至额定点扬程曲线斜线K值(K<1.2)都提出规范及要求。
本文将6级双壳体中开式芯包的高速给水泵作为原始模型,以次级叶轮和涡室为优化研究对象,对原始模型进行数值模拟。在原始模型基础上,对二级叶轮、二级压水室、三至四级过渡流道进行优化设计。无论是数值计算结果还是实测数据,关闭点扬程与设计点扬程的比值均降低,效率提高,实现比值K<1.2的目标值。
在超临界或超超临界火力发电系统中,电动(或汽动)给水泵通常采用双壳体、可抽出泵芯结构(见图1、图2)。由于给水泵是关键核心设备,且泵关闭点扬程对管路系统的选型影响很大,所以一般希望关闭点扬程尽可能低,且关闭点扬程HO与额定点扬程H的比值K应<1.2,此外泵的关闭点功率尽可能小。
在火力发电中常用德国KSB、美国FLOWSERVE、瑞士SULZER、日本荏原EBARA及以日本三菱重工MHI等公司生产的给水泵,其设计的K值基本都<1.2。
德国KSB公司、英国WEIR和瑞士SULZER等公司的给水泵芯包为径向节段式结构,如图1所示。以美国原B.J公司为代表的泵芯包为水平中开式结构,上下两个对称内壳式结构,如图2所示,日本荏原EBARA和日本三菱重工MHI等公司的给水泵均采用美国原B.J公司技术制造。
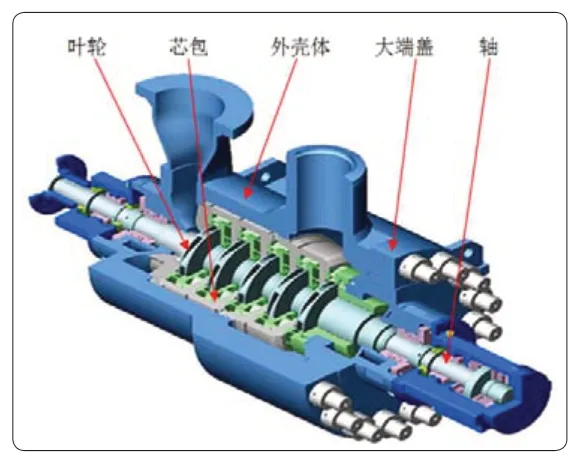
图1 径向节段式双壳体结构

图2 水平中开式双壳体结构
图3所示是国内泵厂生产的某高压锅炉给水泵,内装泵芯是水平中开式结构,上下内壳体为空间流道结构,是一个双壳体6级泵。流量Q=603 m3/h,扬程H=3 007 m(单级扬程527.5 m),转速n=5 575 r/min。与国外品牌如美国FLOWSERVE公司同性能参数的给水泵相比,效率低2.6%,关闭扬程HO约为额定扬程H的1.25倍(即K=1.25),而美国FLOWSERVE公司产品的K值<1.2。本文以国产给水泵次级叶轮和涡室为优化研究对象,拟定如下目标值进行分析与研究:提升效率2个百分点,且降低关闭点扬程HO与额定点扬程H的比值系数K,使K<1.2以下。

图3 内装水平中开式泵芯的国产给水泵
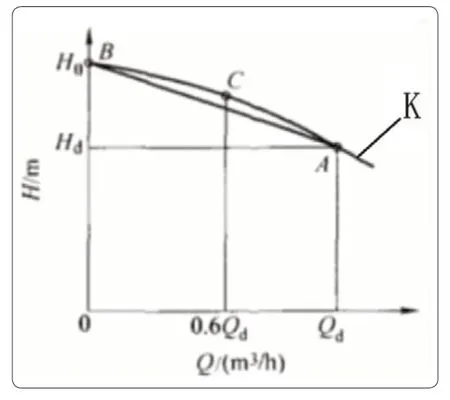
图4 关闭点扬程与设计点扬程之间连线的斜率K
扬程曲线斜率
理论分析
根据叶片泵理论与设计经验,影响关闭点扬程的因素有出口宽度b2、出口角β2和喉部面积等。推导出计算离心泵扬程曲线斜率K的理论计算公式

式中,K为陡降度;n为转速;Q为体积流量;g为重力加速度;b2为出口宽度;ψ2为排挤系数;β2为出口角;ηv、ηh分别为容积效率和水力效率;H为扬程。
斜率K用关闭点扬程与设计点扬程之间连线的斜率的绝对值来表示。由式(1)可知,陡降度的大小与n成正比,与b2、β2及Ψ2成反比,即b2、β2越大,K越小,曲线越平坦,K的大小与叶轮外径D2没有直接关系。这样,扬程表达式可写成。

式中,Ht为理论扬程;u2为叶轮外圆的圆周速度;Qd为设计点流量;σ为绝对速度圆周分量与圆周速度的比值。
由式(2)可知,关闭点扬程HO的值主要由圆周速度u2决定,而u2与D2和n有关 ;设计点扬程Hd的值还取决于K值。经分析可知,可以通过调整b2和β2改变K,即扬程曲线的斜率。另外,通过调整D2可改变扬程大小,使之与原设计扬程相同。
降低关闭点扬程的方法
1.叶片数Z
根据泵的有限叶片数理论,当叶片数减少后,叶片间流道增大,由于叶轮内轴向漩涡的影响,叶轮出口处滑移增加,随流量增加扬程急剧下降。通常叶片数Z<5时,扬程曲线呈单调下降,叶片数增加时扬程曲线平坦,但是叶片数增加会加大扬程曲线驼峰的可能性。
2.叶片出口角β2
在β2<90°时,根据欧拉理论,随流量Q的增加扬程呈直线减小趋势,并且β2越小理论扬程曲线下降得越快。经验表明,在其余参数恰当且出口角小于30°时,扬程曲线单调下降,增加出口角有助于得到平坦的扬程曲线。
3.叶轮出口宽度b2
叶轮出口越小,在某流量点的绝对速度的圆周分量也越小,该点的扬程便越低,使扬程曲线更陡。增加b2有助于获得平坦的扬程曲线,对性能也有好处,但是b2增大可能造成扬程曲线生成驼峰。
4.叶片出口排挤
叶片厚,叶片排挤大,扬程曲线越陡。为了获得无驼峰曲线,增加出口排挤的方法是在叶片背面从进口到出口均匀加厚,以阻塞部分流道。
5.斜切叶轮出口
一般离心泵叶片出口边与轴线平行,由于前后盖板流线长度不同,所以流体流经前后盖板后在出口处所获得的能量也不同,产生了由后盖板到前盖板的二次流,这不但增加水力损失,而且还使扬程曲线容易产生驼峰。因此斜切叶轮出口后盖板,使流经前后盖板的液体所获得的能量基本相同,是减小或消除驼峰的有力措施。
6.叶片形状
叶片的形状显然对扬程曲线的形状有影响。研究表明直叶片可获得扬程陡降曲线,此种叶片形式有助于消除曲线驼峰。三元扭曲叶片可以获得较为平坦的扬程曲线。
7.叶轮进口形状
叶轮进口形状对关闭点扬程和驼峰也有重要的影响。减小叶轮进口直径可减小叶轮小流量时进口的回流损失,同时叶片前伸并减薄可减小叶轮进口的冲击损失,从而提高了小流量时和关闭点的扬程,增加了扬程曲线的稳定性。
8.泵体喉部面积
众所周知,喉部面积越大,关闭点扬程越低,而额定点扬程越高。增大泵体的喉部面积可以得到斜率较小的扬程曲线,但是增大喉部面积也增加了扬程曲线的不稳定性,容易形成驼峰曲线。减小喉部面积对没有驼峰的扬程曲线确实能使其变得更加陡降,但是有驼峰的曲线,减小喉部面积对消除驼峰的效果并不明显。
9.隔舌间隙
减小隔舌与叶轮之间的间隙,可以减小(小流量时)间隙内的环流损失,以及液流从叶轮出口到泵体进口之间的混合损失,有利于提高小流量区的扬程。减小隔舌间隙对提高效率也有好处。
影响扬程曲线形状的因素是多样的,需从叶片出口角、叶轮出口宽度、叶片形状及面积比等几个方面进行研究。
给水泵内流场数值模拟
几何模型
泵芯是水平中开、上下内壳体为空间流道结构的双壳体6级给水泵(见图5),主要由泵筒体、芯包(上下内壳体、首级叶轮、2~5级叶轮及末级叶轮等)和进出口接管等组成。用于数值计算的几何模型(只包括与水接触的过流部件)如图6、图7所示。

图5 6级给水泵结构

图6 泵全流道实体模型

图7 泵部分流道三维实体模型
网格划分
图5所示的给水泵,6级叶轮均为旋转区域,其余部件为静止区域。将6级泵的研究转化为对单级进行研究,将整机分成4个计算域进行分析。对次级叶轮、次级压出室、中间过渡流道及末级压出室进行网格划分。
4个计算域分别为:计算域一为首级计算域(见图8),包括首级叶轮和首级至二级压水室;计算域二为次级计算域(见图9),包括二级叶轮和二级至三级压水室;计算域三为中间过渡流道计算域(见图10),包括三级叶轮和三级至四级压水室及过渡流道;计算域四为末级计算域(见图11),包括末级叶轮和末级压水室。整机性能将通过4个计算域的数值模拟结果进行推断。

图8 首级计算域网格
图9 次级计算域网格
图10 中间过渡流道计算域网格

图11 末级计算域网格
原模型数值计算结果校验与分析
次级叶轮分析与优化
由于次级叶轮和次级压水室对降低关闭点扬程和提高效率的贡献比例最大,因此以次级叶轮和次级压水室为主研究。
以原始次级叶轮模型为基础,调整叶轮叶片型线,主要调节叶片倾角、过流面积分布和叶片包角。为减少模型性能曲线出现驼峰现象,尽量保持前后盖板流线长度一致。优化的叶轮如图12所示。优化的次级叶轮子午线、网格及实体模型如图13~15所示。叶轮内部和压水室的流线分布如图16、图17所示。压水室中间截面的速度分布和流线分布如图18、图19所示。
图12 优化叶轮示意图
图13 优化次级叶轮子午线

图14 次级叶轮网格

图15 次级叶轮实体模型

图16 叶轮内部流线分布

图17 压水室流线分布
图18 压出室中间截面速度分布
图19 压出室中间截面流线
三级至四级流道及末级流道优化
三级叶轮与次级叶轮水力模型相同,三级压水室的半螺旋结构也与次级压水室的半螺旋结构相同。次级模型的优化点在过渡流道的两个转弯半径R1、R2及分流筋板的长度L。三级至四级过渡流道如图20、图21所示。
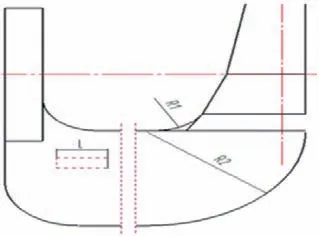
图20 三级至四级过渡流道示意图

图21 三级至四级半流道模型
采用原始叶轮对三级至四级流道进行研究。将此过渡流道优化后的次级压水室模型和优化后的次级叶轮配合进行数值模拟。优化前后数值模拟结果见表1~3。
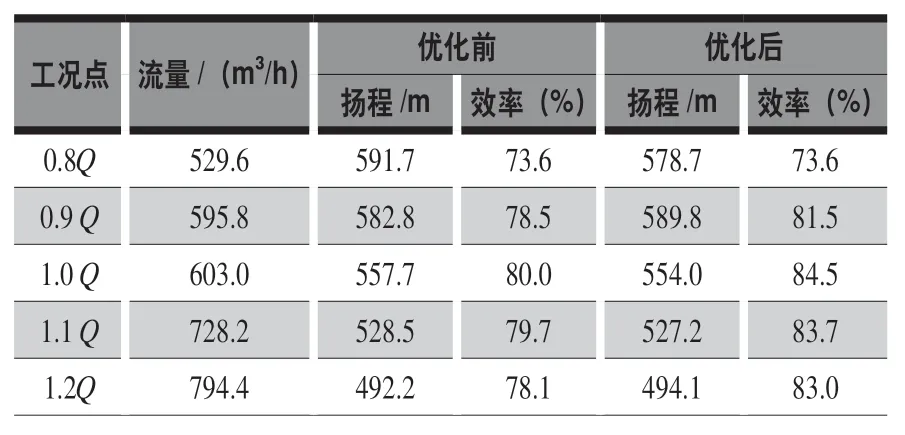
表1 三级至四流道优化前后数值结果对比
对比
泵优化目标参数:流量Q=603 m3/h;扬程H=3 007 m(单级扬程527.5 m);转速n=5 575 r/min;效率η=83%(热态);关闭点扬程HO与额定点扬程H的比值K<1.2。优化后,关闭点扬程与额定点扬程比值对比如图22所示,K值降低0.08;效率对比如图23所示,提升2.9%,超过现有产品。
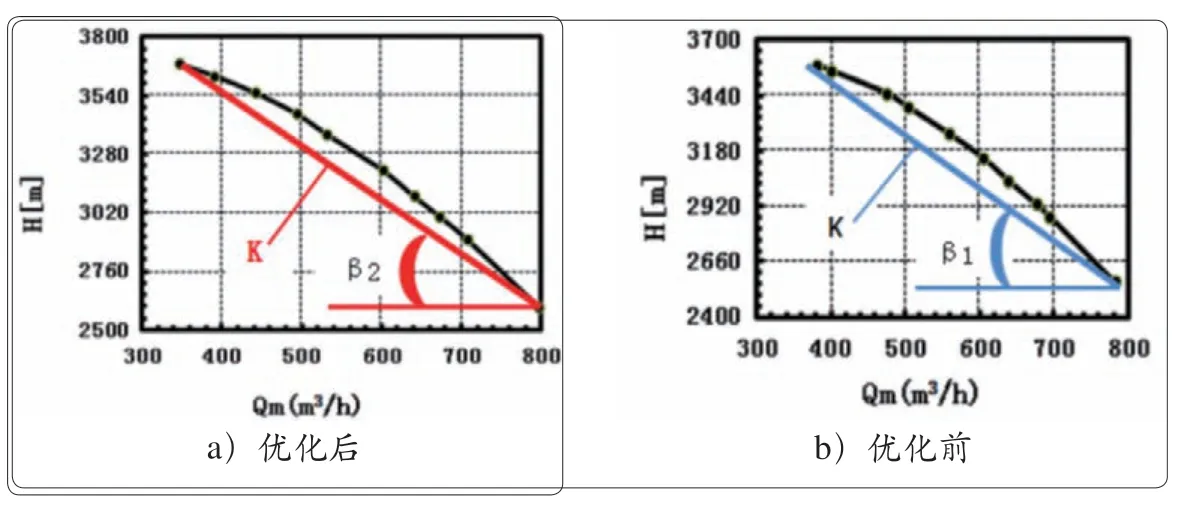
图22 5 575 r/min时扬程曲线对比
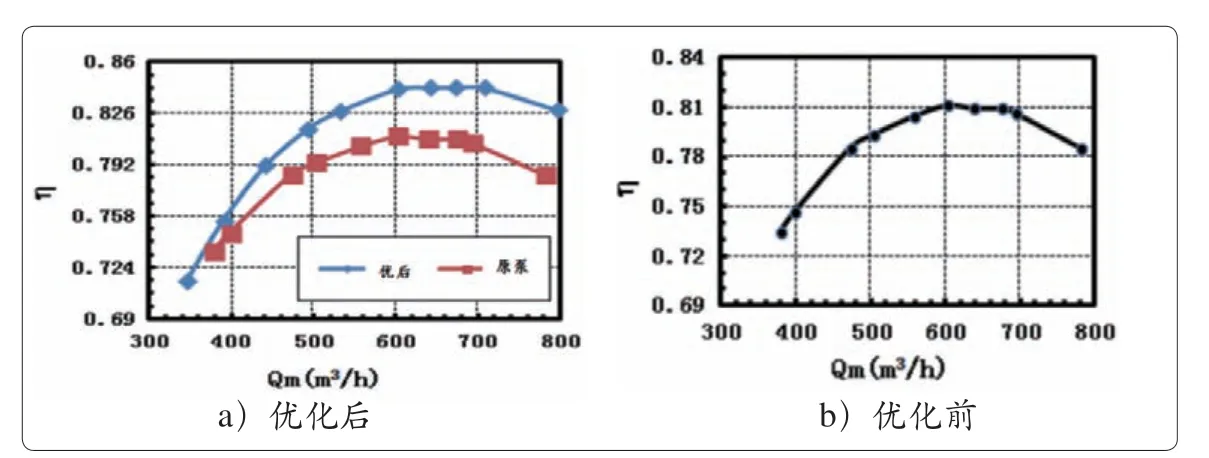
图23 5 575 r/min时效率曲线对比
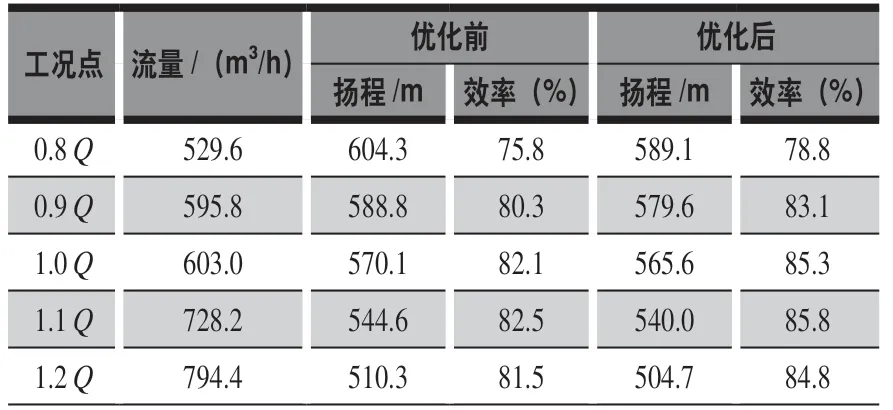
表2 末级优化前后数值结果对比

表3 整机优化前后数值模拟结果对比
结束语
总结了降低关闭点的方法,并通过数值模拟进行进一步研究,在得到扬程曲线斜率系数减小的满意结果后,对提升泵效率进行优化研究,最终达到关闭点扬程与额定点扬程比值K减小0.08和效率提升2.9%的目标。
总之,通过对6级给水泵原始二级叶轮、二级压水室、三至四级过渡流道模型优化,对减小关闭点扬程曲线系数K是行之有效的方法之一。优化产品案例及用户现场应用证明,减小比值K值对电厂系统运行平稳、降低泵关闭点功率及全生命周期LCC管理等效果显著。
