浅议习题教学中的常见操作误区

吴立新

[摘 要]有些教师面对教学疑点，或沉默以对，或浅尝辄止，或生搬硬套，或斷章取义。文章通过四个案例说明，教师只有不唯分数论学生，扎实教学，才能为学生的终身发展服务。

[关键词]教学误区;沉默以对;浅尝辄止;生搬硬套;断章取义

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）23-0044-02

笔者常常在办公室与同事交流教学心得，关于习题教学，有些教师心中疑虑重重：“对于某些易错点，有时候讲多了反而起反作用，精讲倒不如略微提及，苦口婆心倒不如蜻蜓点水。”此言一出，立即引发许多教师的共鸣，并竹筒倒豆子般列举一大堆证据，附和该言论。笔者现撷取四例加以评述，以期与广大教师同仁探讨。

一、沉默以对

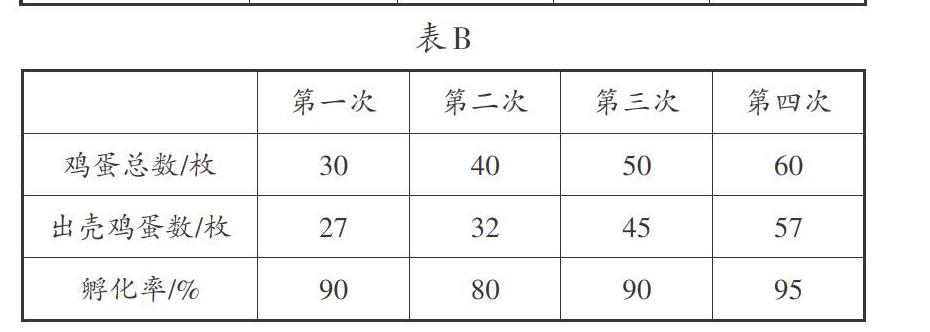
【例1】下面是生物小组同学开展的人工鸡蛋孵化实验的情况。请根据表中数据计算出每次的孵化率，并填入表格中。

教师发现，学生在填写鸡蛋的孵化率时出现了两种细微的差别（见表A和表B）。

（据统计，某班有近90%的学生得出了“表A”。但很显然，“表B”更加规范。）

观察表格，不难发现，在表头中已经统一了数量单位和百分号，填写数据时直接默认沿用上述单位符号，无须赘述。而绝大多数学生忽略了这一点，惯性使然，下意识地添加了百分号。面对这两种书写格式，教师评阅时也很矛盾：对于“表A”，如果不留情面地评定为“错”，势必会传递出“书写百分数时不该写百分号”这样的信号;如果于心不忍而评定为 “对”，似乎又不够严谨。

经过大家的深入讨论和集体研究后，达成一致意见：为了不给学生留下“百分数可以不写百分号”的负面暗示，对上述两种形式的答案都应“大开绿灯”。另外，为了谨防“表A”和“表B”引发学生的矛盾与纠结，在讲评时，教师用“沉默不语”的方式来应对，以防越描越黑——好意提醒反而暗示学生去过度注意和辨析两种形式的异同，并导致他们深究。

其实，面对这种练习，教师大可不必如此费神，只需三言两语就可以将需不需要带百分号说清楚——如果表头有百分号，填数时就不必另写;如果表头没有百分号，填数时就要写。如此简单的问题，部分教师因害怕言多必失选择了沉默，反而弄巧成拙。

二、浅尝辄止

【例2】关于“方程”，有这样一道例题：移动5G信号塔高64米，比移动3G信号塔高度的2倍少22米。移动3G信号塔高多少米？

教学中，教师先让学生探查“等量关系”，然后列方程解答，即根据“移动3G信号塔的高度×2-22=移动5G信号塔的高度”列方程为：2x-22=64。而后，通过练习巩固，使学生迅速掌握此类方程的解法。对于这种题型，教师多采用该模式教学，鲜有拓展延伸，很少涉及方程的不同列法、不同算法等。究其原因，教师认为这是方程的经典题型，是高频考点，为了确保得分率，最好不要节外生枝，老老实实地按照正统解法教授，“不求多样，但求无错”。

即便有学生提出“（64+22）÷2”这样的解法，因为考虑到这种方法极易扰乱思维，引发将相对量多与少的对应关系颠三倒四，将倍量与增量的先后顺序交叠错乱，出现诸如“2[x]+22=64”“64÷2-22”“64÷2+22”等错解，所以在教学中，教师见好就收，不敢深入研究，更不敢多角度拓展。

众所周知，学生对知识产生负迁移是一种自然现象，作为教师，应理性对待、因势利导。随着时间的推移，学生的认知水平会逐步提高，会自我纠正认知偏差，自我调节不良心理暗示，但一些教师为了追求效率，阻截了学生生成灵性答案的通道。

三、生搬硬套

笔者曾听过一位教师执教的“圆的周长”一课。新授内容结束后，教师归纳总结圆的周长公式：C=πd和C=2πr，并留出几分钟时间让学生背记，接着给出巩固练习：一个圆形的煤渣跑道的半径为2.5米，沿着这个煤渣跑道晨跑一圈，一共要跑多少米？话音刚落，就有几名学生举手示意，许久，全班学生才接二连三地举起了手。为何少数学生反应如此神速，而其他学生却有些迟疑？笔者详查了学生的练习，才揭开谜底：根据圆的周长公式“C=2πr”，大部分学生严格套用公式列式为“2×3.14×2.5”，只有少数学生灵活处理成“2×2.5×3.14”。

可能是因为初次接触圆的周长公式，学生计算时过于紧张，竟然连摆在眼前的简便计算（可先算2×2.5）都未能看出。对于数学中的字母公式，许多教师都有宝贵的教学经验，但有部分教师只把“记”和“用”奉为圭臬，往往只要求学生牢记公式形式和各字母的含义，然后代入数据套用。至于公式中各元素的换算关系，他们认为应用价值不大，讲多了反而不利于对公式的牢固记忆。由于学生没能理解公式的深层含义，导致运用时死板僵化，不能灵活运用。

四、断章取义

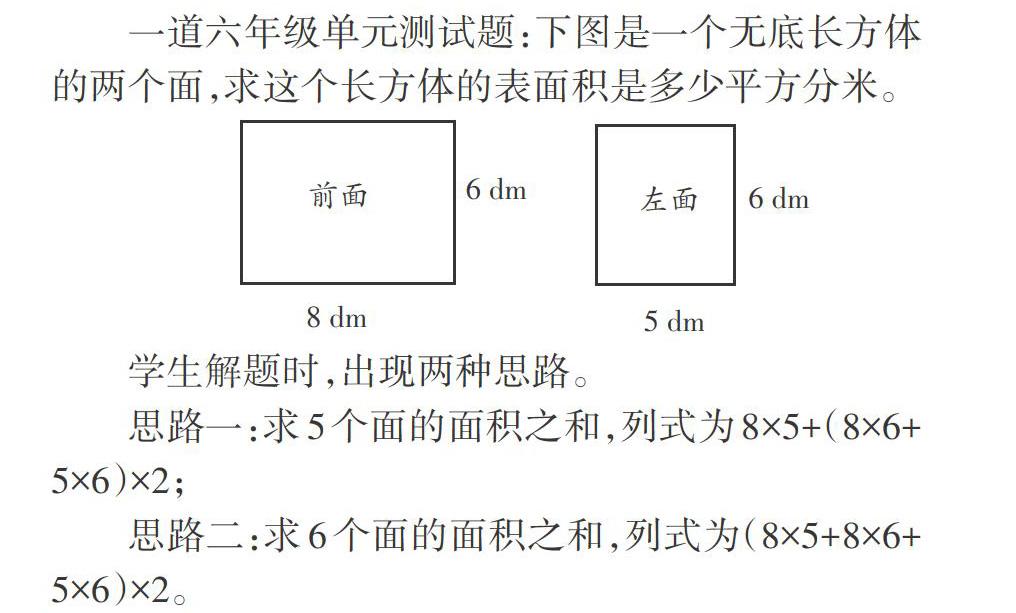
一道六年级单元测试题：下图是一个无底长方体的两个面，求这个长方体的表面积是多少平方分米。

学生解题时，出现两种思路。

思路一：求5个面的面积之和，列式为8×5+（8×6+5×6）×2;

思路二：求6个面的面积之和，列式为（8×5+8×6+5×6）×2。

这道题的本意是要考查学生的审题能力，以及对表面积的灵活解读能力。部分教师认为题中已经明确“无底”，就应该严格遵照出题者的意图，去掉底面，求出5个面的面积之和;至于题中表述的“表面积”一词不必深究，而是要根据具体语境灵活解读，迎合出题人的意图。

其实，数学题必须兼顾科学性和严密性。该题中的“无底”和“表面积”两个词眼是要斟酌的。什么是表面积呢？经过广泛查证，笔者发现“百度百科”所给的定义比较中肯和严谨，即所有立体图形的所能触摸到的面积之和叫作它的表面积。按照这个定义，要计算一个无底长方体的表面积，除了要算上外面的5个面，还要算上里面的5个面，即里面和外面的面积和，因为它们都是可以触摸到的。也许，出题者对“表面积”的定义本就一知半解，“无底”二字又易造成歧义，使一道题出现三种可能的答案。面对这样“粗制滥造”的试题，教师不追究题目本身的问题，反而削足适履，让学生人遗憾。

可见，教学中教师应该敞开心扉，竭诚为学生的终身发展服务，不能盲目追求短期的考试高分，而应该为学生展开一幅广阔的知识画卷，且教且珍惜。

（责编 罗 艳）