结构化教学，让数学学习走向纵深处

高丽君

[摘 要]深入分析多个版本教材的正方形数相关内容，发现正方形数的教学具有复合性、系统性、连贯性的特点。在此基础上，重新定位教学目标，调整教学策略，从整体视角上引导学生发现乘法表的对称性，认识正方形数，丰富学生对乘法的认识，培养学生的结构化思维。

[关键词]正方形数;结构化;数形结合;探究意识

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）23-0010-04

【课前慎思】

北京版教材数学百花园“有趣的数”位于表内乘除法之后，教学内容是正方形数，标题里有两个关键词——有趣、数。“有趣”体现在数形结合，并以形命名数;“数”则特指正方形数。为什么要讲正方形数呢？因为学生已掌握表内乘除法，具备了初步的计算能力，很显然，这里的计算并不是简简单单的口诀计算，还需要兼顾知识要素和推理、验证等能力要素。

为什么北京版教材有这个内容呢？它是独立的设计吗？查阅了各个版本教材（如图1-1、1-2、1-3）后发现，虽然其他版本教材没有把正方形数的内容作为独立课时，但在期末复习或单元复习时都或多或少地体现了正方形数，说明这一内容并不是孤立存在的，而是学习完表内乘法之后需要掌握的知识。显然，这节课具有复习巩固作用的复合功能，它是以正方形数作为媒介，培养学生的结构化思维，促使学生主动迁移运用已学知识，打造知识网络。

（2）5乘几，积个位上的数字有哪些？

在这节课上学生需要形成哪些能力？数学课程标准指出：教师应帮助学生在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法，获得广泛的数学活动经验。如课题所言，首先，这节课是有趣的，有趣是学习真正发生的土壤;其次，这节课要在轻松愉快的环境里培养学生提问的意识，提升学生的团队合作能力、自主探索能力和独立创造能力，使学生学会正方形数后能把这种学习的方法迁移到三角形数、五角形数等的学习中，并在这个过程中学会猜测、验证、推理，毕竟知识易得，能力难培。

【教学目标】

1.从整体视角上引导学生了解乘法表的填数规则，沟通乘法口诀与乘法表的联系，丰富学生对乘法的认识，进一步巩固表内乘法的运用。

2.在研究乘法表的过程中让学生用语言表述探究过程，发现乘法表的对称性，认识正方形数，及其在乘法表中的分布特点，渗透数形结合思想。

3.以学生为中心，在分享、交流、互动、质疑中，提升学生的数学表达能力和思维水平，增加学生的学习兴趣。

【教学过程】

1.在更“大”的范围里，认识乘法表的填数规则

师（板书“数”）：这节课我们将认识一个伟大的数，大家在小学中学的第一个数就是它，其他数都是在它的基础上一点一点加出来的，知道它是谁吗？

生（齐）：1。

师：1可以表示什么呢？（学生答，略）

师：1可以表示任何数量是1的东西，也能表示一个正方形，从乘法含义的角度来看，一个正方形就是1个一，对应乘法算式1×1=1，口诀“一一得一”。

师：按照数数的规则，每次增加1，即可得到2、3、4、5、6、7、8、9。（数形结合，依次复习1的乘法口诀和含义）最后，在9的基础上加1，就是10个一（链接一年级知识“10个一就是1个十，即10”）。因此，不管是1个十，还是10个一，都可以通过相同的乘法算式计算出来：1×10=10×1=10。

师：如果现在有100个方块，是一直往后摆容易看出来，还是用其他方法更好呢？

生1：《蚁国迁徙记》有一句经典台词——哇，好长的队！另起一行摆放会更容易看出来是多少个方块。

师（一行一行出示方格图，让学生数，如图3）：2个十是2×10=20，3个十是3×10=30，4个十是4×10=40……9个十是9×10=90，10个十即10×10=100，说明这个大正方形里有100个格子。

师：如果要把它们编成口诀，该怎么编？

生2：一十得十，二十二十……十十一百。（学生编着编着便笑了）

师：笑什么？知道为什么没有10的乘法口诀吗？

生3：它比乘法口诀更简单，所以不用专门学啦！

师：刚才是横着一行一行地看，由横竖相乘算出的，竖着看呢？

（学生再次一列一列地数，并熟悉计算法则，结合整十数的含义，得到最上一行乘法表的结果，巩固乘法表的计算规则。）

【设计意图：国内任何版本教材均不直接教1的乘法口诀，默认学生会在2～9的口诀学习过程中自然习得，但对于低年级学生来说，至少需要有链接的过程，才能巩固其对知识的理解能力;同样，除了沪教版教材有专门的除数是10的除法这一课，国内大部分版本教材也不专门教10的乘法口诀，默认学生学习100以内数的认识时已掌握，但低年级学生的认知情况显示，知识的迁移运用需要教师专门引导，不应认为学生理所应当掌握。此外，这里通过数形结合的方式正好可以解释九九乘法口诀表为什么没有10的乘法口诀。“在更‘大的范圍里”就是指在10×10的乘法表里进行探究。】

师：这里的大表格是10×10的正方形，请用前面的规则填写剩下的空格。（给学生2分钟时间自主完成，能填多少是多少）

师：运用1的乘法口诀观察图5最左一列和最下一行的空格的填法，再用2的乘法口诀验证发现。

生4：不管是竖着填，还是横着填，算出来的结果都一样。

生5：这让我想起了乘法口诀，乘法口诀都是小的数在前，一句口诀可以替代两个乘法算式，所以不需要全部都写上。

师（对称轴用红线，表示乘法表的对称性）：这个对称轴很了不起啊，沿着它对折，你发现什么？

生6：两边的数刚好能重合。

【设计意图：在巩固乘法表的填写规则的过程中，从特殊到一般，引领学生发现乘法表中的对称现象，进而将这一发现与乘法口诀的编制法则结合起来。学生通过深度思考，理解了九九乘法口诀表为什么是“三角形”，而不是“长方形”，从而深入理解知识。此外，通过横、竖两个方向巩固乘法表填写规则的过程，表面上看是计算小正方形的数量，实际上是加强乘法口诀与面积的关系，为学生学习三年级的面积打好基础。】

2.数形结合，探索正方形数

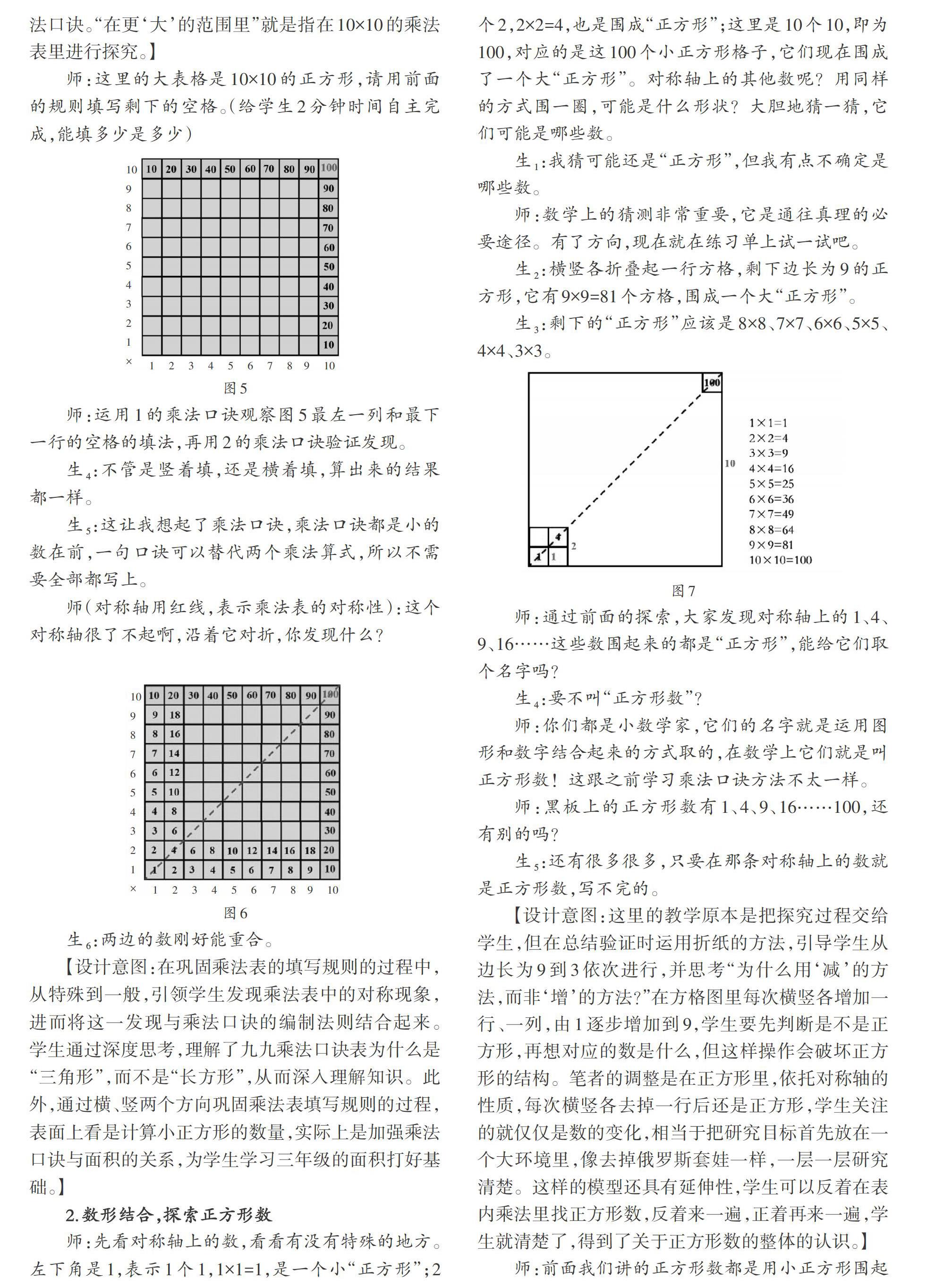
师：先看对称轴上的数，看看有没有特殊的地方。左下角是1，表示1个1，1×1=1，是一个小“正方形”;2个2，2×2=4，也是围成“正方形”;这里是10个10，即为100，对应的是这100个小正方形格子，它们现在围成了一个大“正方形”。对称轴上的其他数呢？用同样的方式围一圈，可能是什么形状？大胆地猜一猜，它们可能是哪些数。

生1：我猜可能还是“正方形”，但我有点不确定是哪些数。

师：数学上的猜测非常重要，它是通往真理的必要途径。有了方向，现在就在练习单上试一试吧。

生2：橫竖各折叠起一行方格，剩下边长为9的正方形，它有9×9=81个方格，围成一个大“正方形”。

生3：剩下的“正方形”应该是8×8、7×7、6×6、5×5、4×4、3×3。

师：通过前面的探索，大家发现对称轴上的1、4、9、16……这些数围起来的都是“正方形”，能给它们取个名字吗？

生4：要不叫“正方形数”？

师：你们都是小数学家，它们的名字就是运用图形和数字结合起来的方式取的，在数学上它们就是叫正方形数！这跟之前学习乘法口诀方法不太一样。

师：黑板上的正方形数有1、4、9、16……100，还有别的吗？

生5：还有很多很多，只要在那条对称轴上的数就是正方形数，写不完的。

【设计意图：这里的教学原本是把探究过程交给学生，但在总结验证时运用折纸的方法，引导学生从边长为9到3依次进行，并思考“为什么用‘减的方法，而非‘增的方法？”在方格图里每次横竖各增加一行、一列，由1逐步增加到9，学生要先判断是不是正方形，再想对应的数是什么，但这样操作会破坏正方形的结构。笔者的调整是在正方形里，依托对称轴的性质，每次横竖各去掉一行后还是正方形，学生关注的就仅仅是数的变化，相当于把研究目标首先放在一个大环境里，像去掉俄罗斯套娃一样，一层一层研究清楚。这样的模型还具有延伸性，学生可以反着在表内乘法里找正方形数，反着来一遍，正着再来一遍，学生就清楚了，得到了关于正方形数的整体的认识。】

师：前面我们讲的正方形数都是用小正方形围起来的，除了正方形，还能不能用别的形状？

生6：教材上是用红点代替，但我觉得用什么形状都行，例如花、三角形、爱心都可以，主要是要按照这样的规则摆。

（学生做教材上的题目，填写积是1、4、9、16的算式时根据点子图温习正方形数的特点，填写积是25的算式时需要按顺序想象，思考剩下的正方形数是什么以及对应的点子图的形态。这与前面的学习过程刚好相反，达到及时巩固的作用。）

出示正方形数的其他研究方案：

师：学完正方形数，你能给这节课取个名字吗？

生7：有趣的正方形数、好玩的正方形数、有规律的正方形数、神奇的正方形数、神秘的正方形数……

3.拓展延伸，认识更多有趣的数

师：这节课很特殊，是到现在为止唯一一节与形状联系起来命名数的课，也就是正方形数，它是一个非常好的数形结合的例子。用数形结合的方法除了可以探索正方形数，还可以研究什么数？猜一猜，通往真理的道路都是猜出来。

生1：三角形数、五边形数、六边形数等。

出示课件：

师：无论你研究以上的任何一种数，都应该从几开始研究？

生2：从1开始研究，它最特殊。

师：是的，就像这节课的课题——有趣，以前我们学过有趣的数，今天学了有趣的数，未来还会有很多有趣的数。所以这节课只是给你一块敲门砖，教给你研究数的方法，希望你能保有好奇心，坚持研究下去，未来数学史上可能会留下你的名字哟！这节课给你最大的感受是什么？

生3：以前我觉得数字跟形状无关，现在发现不但关系密切，还可以用形状给数命名。

生4：现在知道居然有这么多用形状命名的数，很惊讶！

生5：数学无处不在，规律也是无处不在的，要善于发现。

【设计意图：一节课只有40分钟，时间非常有限，所以每一节课都应像一粒种子，只有这样，它才能具有蓬勃的生命力，有无限可能。本节课对于正方形数的研究，着重构建由点成线、由线成面的学习模型，为学生学习面积单位打下基础，并基于学情适当拓展至普遍性的学习，学生能够形成探索数学问题的兴趣与欲望，开阔视野。教师在探索过程中非常注重学生解决问题能力的培养，让学生感悟到学习数学、应用数学的乐趣，感受数学的价值，增强学生学好数学的信心。】

【本文系北京市大兴区教育科学“十三五”规划课题“小学数学长线融合项目的实践研究”阶段性成果（课题批准文号：19GHX002）。】

（责编 金 铃）