课时教学

摘  要：目前，教师主要将“大概念”应用于整体知识教学的单元教学设计中，而忽视“大概念”在课时教学中的渗透. 然而，要想突出整体知识的教学，必须将“大概念”教学理念落实到课时教学的各个环节，需要在教师的教学主张，以及学生的知识形成、理解、应用过程中不断渗透，才能使其潜移默化地转变成学生的学习方式.

关键词：大概念;课时教学;学习方式

新课程教学以单元教学设计为抓手，以“大概念”为设计视角，突出强调知识的整体性和学生学习的整体性.“大概念”可以帮助学生将各个知识点联系起来.“大概念”作为教师教学的得力助手，发挥着“概念魔术贴”的作用. 但是，教师的具体课时设计（尤其是新授课）中往往很少出现“大概念”的身影，教学中更多的仍然是知识的罗列，长此以往，很可能又回到碎片化教学的老路. 很多教师虽然有单元设计知识联系的热情，但缺乏在课时教学中落实“大概念”的行动，新授课的设计仍是单元、课时两张皮，学科“大概念”的统摄和引领作用没有得到较好的滲透，知识的整体性未能凸显. 对一线教师来说，课要一节一节上，不可能利用一节课完成一个单元的教学，单元教学设计是对单元的整体构想，具体落实要依赖每次课时教学中的不断渗透. 分散到每节课如何渗透“大概念”，才是体现知识与学习整体性的关键，也是最需要落实的教学行动.

本文着重谈谈笔者对在新授课中渗透“大概念”教学的一些做法与体会，希望能引起大家探讨的热情，更希望提出批评意见，以便我们的研究能得到更好的发展.

一、在教学主张中渗透“大概念”

“大概念”教学是体现学科专家思维的教学，是教会学生如何进行思考的教学.“大概念”也被一些学者翻译为“大观念”. 应该说，“概念”的确是“大概念”的重要形式，但“大概念”不局限于此，它还包括“观念”“论题”等含义.

教学主张是教师的学科教学观念，对学生来说是最直接的“专家思维”. 因此，教师要有自己的学科教学理解，要把自己领悟到的专家思维，在课堂上不断地渗透给学生，让学生有一个行之有效的方法学习数学知识. 笔者认为，暴露思维和用数学方法论指导教学是有效的教学模式. 为此，笔者一直坚持师生相互暴露思维，在思维过程中教会学生思考;利用强、弱抽象，映射反演，CPFS理论演示数学知识的产生和研究过程. 现在看来，这和“大概念”教学理念不谋而合.

在新授课教学中不断展现“特殊—一般—特殊”的探究过程，“具体—抽象”相互协同的思维过程，“既教猜想，又教证明”的推理论证过程，引导学生逐渐了解数学研究的“基本套路”.

在理解知识的过程中强调“举个例子”帮助学生直观形象地理解知识，“单个对象研性质，多个对象找关系”，促进学生对知识的扩散式理解，主动寻找研究对象.

在解题教学中提出“函数、不等式、方程是一家”“数形一体、动静结合”，强化知识的联结与转化. 这些“大概念”的有机渗透会对学生产生潜移默化的影响，使得学生在遇到新情境、新问题时也会主动尝试、大胆探究，形成自己的理解，触动个性化“学生‘大概念’（知识理解、方法、理念）”的生成，进而能在较大范围内解决数学问题，将离散的知识结构化.

二、在知识形成的过程中渗透“大概念”

数学知识的形成过程是人们对数学知识逐步深入、连续理解的过程，往往是漫长的. 在这个过程中会不断出现“大概念”的身影，教师要善于捕捉隐藏在历史中的“大概念”，并在教学过程中适当还原历史进程，用知识发展的连续性增强学生的全局观和正确的学科发展观.

函数概念的形成过程是极为典型的“大概念”渗透过程. 人类从原始的结绳计数抽象出数字，从数字抽象出字母，再抽象出变量，进而抽象研究两个变量之间的依赖关系，随后发展成变量对应说、集合映射说. 在这个过程中，进行了连续的数学弱抽象，形成了不断扩张的“大概念”，概念的适用对象不断扩充，概念也不断精确、精致. 后来，又进一步抽象到广义函数，形成分布理论、函数空间与拓扑，以及泛函分析中的变换、同胚、算子等重要而基本的概念.

在“函数概念”的新授课中，教师可以借助历史上的典型函数[y=1，y=1，x∈Q，0，x∈∁RQ，] 将初中的函数变量说概念抽象为上位的集合对应说，适当再现“大概念”的形成过程，体现“大概念”对知识属性的提炼、抽象功能，让学生感悟到数学“大概念”自觉修正和主动扩张的开放性，体悟数学概念的创新方式，培养学生自我追寻“大概念”的学习能力.

学生在“大概念”的形成中解决迫切需要解决的问题，主动建构有明确意义的知识，这样的知识更容易被学生认同、接受，以及长期保留.

基于“大概念”的统摄引领，不同历史发展阶段对同一知识的理解也会出现不一样的视角，借助历史发展丰富知识的理解方式，有利于学生形成深刻的图式理解，构建扩散的知识网络.

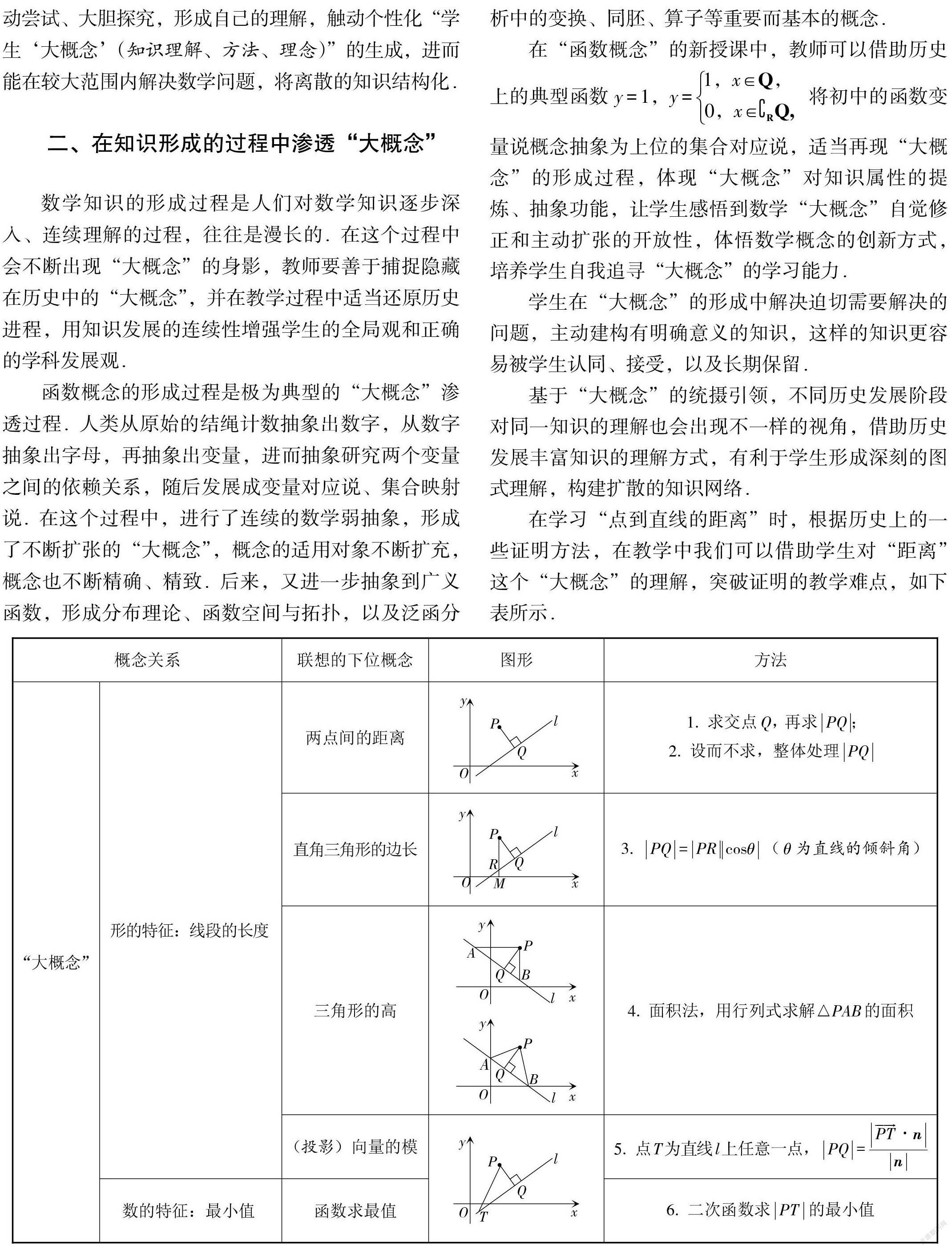
在学习“点到直线的距离”时，根据历史上的一些证明方法，在教学中我们可以借助学生对“距离”这个“大概念”的理解，突破证明的教学难点，如下表所示.

在“距离”这个“大概念”的统领下，上述方法之间相互关联，其中方法2、方法5和方法7是相通的，可以相互沟通促进学生的理解.

通过“大概念”的教学组织，借助“大概念”的统摄发散功能和小概念的反哺作用，学生很容易形成各种想法，得到视角不一的问题解决方案，同时强化了上、下位知识间的联结，构建了层次丰富、多向延伸的知识网络，促进了学生对所学知识的立体化理解. 通过“大概念”将分散的数学知识串珠成链，丰富学生问题解决的途径，推动学生对数学知识的整体理解. 借助“大概念”在知识形成中的有机渗透，促进学生由知识的解读式学习向知识的建构式学习转变，由单调肤浅的练习式学习向丰富深刻的实践式学习转变.

三、在知识理解的过程中渗透“大概念”

数学知识的理解是一个系统性工程，需要相关知识的前联后铺，在这个过程中，知识联结越广泛越能形成深刻理解，越能形成四通八达的知识网络，越能建立结构稳定、有序合理的知识框架，在应用的过程中越容易被激发和带动.

数学概念的学习过程是“大概念”渗透最有力的过程. 在概念的形成和理解过程中必然会促进对上位“大概念”的理解，在与其他并列概念的组合关联中必然会综合应用上位“大概念”和产生新的下位“小概念”. 概念的理解过程，就是一个以所学概念为结点的上、下位知识联结的过程，也是知识不断向外扩散的过程，是一个以“大概念”为统领知识紧密关联的过程，是知识结网、整体学习的过程.

首先，挖掘概念的等价形式和构成要素间的等价变换，形成同位概念，将单一的概念抱成“团”，以丰富的概念表达来体现“大概念”的“大”. 例如，向量数量积：两个向量[a，b]的模及其夹角[θ]余弦的乘积[⇔][⇔][a · b=abcosθ⇔a · b=x1x2+y1y2.] 这就实现了文字定义、符号表达、坐标表示三者间的等价转换，应用时可以根据不同的背景选择恰当的形式. 从要素的组合变换上，可得[a · b=abcosθ=abcosθ=][acosθb=bacosθ=b · a，] 轻松证明了交换律. 量的不同组合，可以带来不同理解，产生不同的性质，同时隐藏着向量投影、模的乘积、夹角等下位概念;[cosθ=a · bab=x1x2+y1y2x12+y12x22+y22]体现了夹角与数量积两种形式的联系，加强了不同形式定义之间的关联，深刻了向量方向的内涵;[acosθ=a · bb， bcosθ=][a · ba]自然带出了下位概念向量投影的代数形式，为解释几何意义做好了铺垫. 概念的等价变换，展现了概念的不同侧面，丰富了概念的表现形式，增加了概念的“触角”，为概念的生长提供了多种可能，有助于对概念的整体理解.

其次，借助“大概念”的统摄和引领功能，从“大概念”的构成要素出发，自觉分析所学概念在这些要素上的表现，加强对所学概念性质的挖掘，促进深刻理解，提升概念的应用价值. 从“向量”这个“大概念”考察，我们就容易从方向（夹角）、大小（模）来研究数量积，形成一些新的性质（下位概念）. 从方向上考虑：[a，b]同向[⇔][a · b=ab，] [a，b]反向[⇔][a · b=-ab，] [a，b垂直⇔a · b=0.][⇔] 从模的关系考虑：[a=b⇔a · b=a2=a2， a=1⇔a · b=bcosθ]（投影的几何意义）. 借助“大概念”的组成要素所提供的研究方向，通过强抽象的方式探究概念的性质，形成新的“小概念”，使所学概念变得更加饱满，应用也更加广泛，同时“大概念”的统摄对象也随之丰富.

最后，借助“大概念”统摄下并列概念的相互融合，横向拓展所学概念的价值，扩充“大概念”的内容，创新“大概念”的性质，形成新的综合性“小概念”，增强所学概念的辐射功能. 在“向量运算”这个“大概念”的统摄下，将数量积与加减、数乘融合，就很自然地形成了[a±b ∙ c=a ∙ c±b ∙ c， λ±μ ∙ c=][λc±μc， λa ∙ b=][λa ∙ b， λμ ∙ a=λμa=μλa]等运算法则，以及[a+b2=a2+2a ∙ b+b2， a+b ·][∙a-b=a2-b2]等运算公式. 在证明相关性质时，站在“向量”这个“大概念”的角度，自然也会有数形双视角. 例如，[a+b ∙ c=a ∙ c+b ∙ c]的证明. 教材用了投影和相等的几何视角，如果用坐标化的代数视角，设[a=x1，y1，b=x2，y2，c=x3，y3，] 则[a+b ∙c=x1+x2 ·][x3+y1+y2y3=x1x3+y1y3+x2x3+y2y3=a ∙c+b ∙ c.] 比几何方法更容易想到. 通过并列概念之间的融合，可以促进对几个概念的综合理解，产生多种研究对象，既能提升学生对知识的整体认知，又能提高学生解决新问题的能力. 在“大概念”下实行知识之间的跨界融合，更能形成创新的研究对象. 有了“大概念”的引领，学生的学习空间会得到极大的拓展，这种拓展促进了学生的主动思考，给学生带来了精神震撼和心理满足.

四、在知识的应用过程中渗透“大概念”

学生学习能力的强弱主要体现在知识迁移水平上，把所学知识应用到新情境中的能力就是迁移. 迁移的关键是形成知识关联，学生的知识关联越广、越深刻，形成的知识网络就越牢固、越丰富，知识迁移就越容易发生.“大概念”就是学生认知网络中极重要的穩固结点，是激活其他知识的关键，是学生理解新知识的有力抓手，也是学生形成创新能力的核心力量.

在新授课的知识应用和例题学习过程中渗透“大概念”，既可以强化学生对新学知识的理解，也能在“大概念”知识的联结中促进学生对其他知识的理解与融合，促进知识网络的主动建构，增强知识的整体性和灵活性. 例如，在“向量基本定理”中有一道非常经典的例题.

从“大概念”出发，首先让学生丰富等价知识，从而增强对所研究问题各种表达形式的理解和联系. 在“大概念”的指引下，学生经过讨论，形成了比教师最初构想更丰富的等价联结，如图1所示.

在原问题的解决过程中，学生依据“大概念”的指导，分别从向量基本定理、向量运算这两个上位概念，形成了不同的解法. 作CE平行于OA，交OB于点E，简解如图2所示.

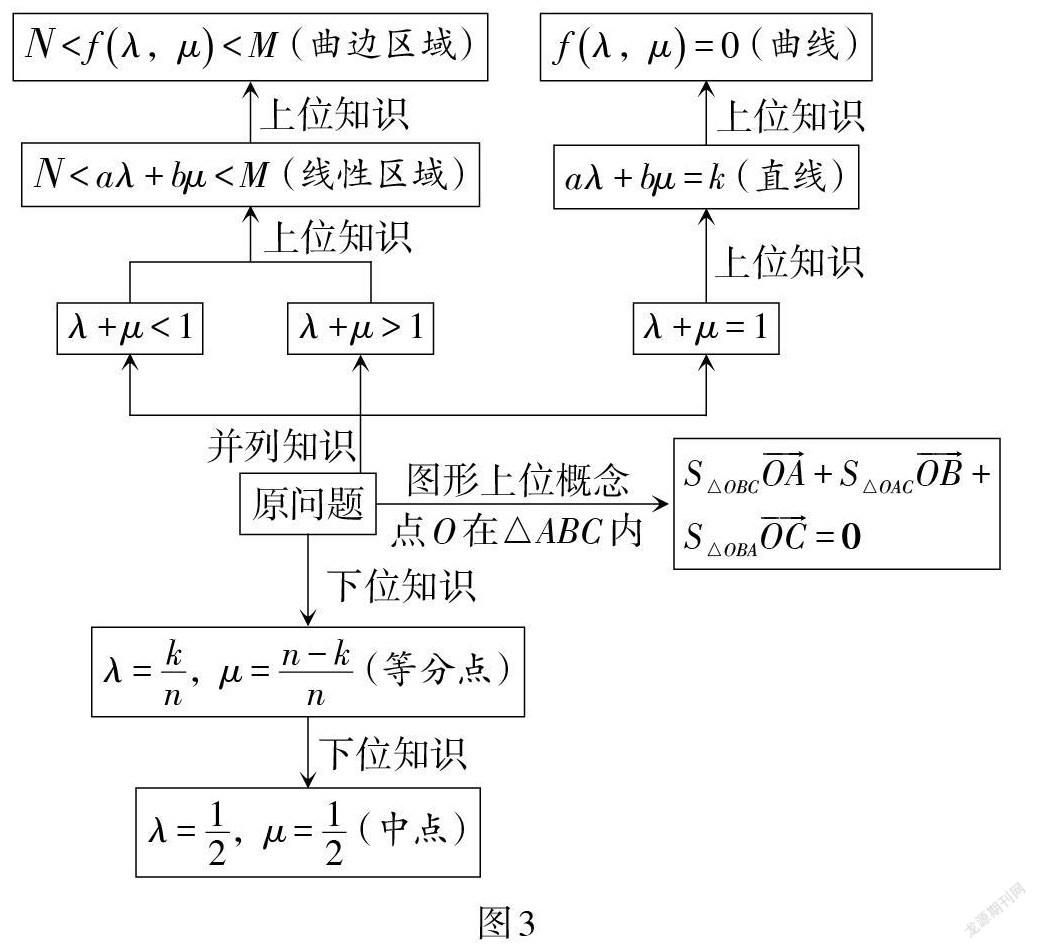
整个解题过程由于有“大概念”的参与，思路的形成非常自然、便捷，同时使学生对上位概念的理解有了提升，特别是加强了不同上位概念之间的勾连，形成了一个相互连通的整体网络，为知识的提取提供了更大的空间和可能. 学生还联想了原问题的并列知识，并激发形成了具有统摄作用的“大概念”知识谱系，甚至创新了“大概念”. 课堂上师生相互激发形成的“大概念”教学谱系图如图3所示.

学生通过“大概念”的引领，改变[λ，μ]的线性关系，促进了深度学习的开展，深入理解了各种代数变化的图形内涵，建立了完美的数形联系. 值得一提的是，有学生创新地提出了[λ2+μ=1，] 瞬间激发了教师对一般曲线的联想，进一步提升了“大概念”的层次.

知识应用阶段的每一次“大概念”教学，都是不断强化知识联系的过程，也是对知识内核进一步提升的过程，是师生形成整体认知最明显的过程，是解题教学最为便捷有效的过程. 基于“大概念”的知识应用教学，是最能触动学生参与的教学方式，是最能触摸知识本质、形成深刻理解，构建联结广阔、提取自如、开放有序的知识网络，建立有个性、有深度的知识体系与思想方法的教学方式.

在“大概念”教学中，教师不再是学科知识的传声筒，而是学科专家思维的领悟者、实践者，是学生学习专家思维的领路人、合伙人. 在教学中，教师不仅要有“大概念”设计教学的意识，更要有用“大概念”组织学生学习的能力，要在每节课、每个学习节点设计有利于学生使用、提炼“大概念”的环节，加强知识的主动生成，不断培养学生知识的整体性、认知的连贯性、学习的可持续性，提升学生解决数学问题的能力，增强学生以数学知识解决现实问题和跨学科问题的能力，将培养学生数学学科核心素养落实在教学的每个细节上.

参考文献：

[1]格兰特·威金斯，杰伊·麦克泰格. 追求理解的教学设计（第二版）[M]. 闫寒冰，宋雪莲，赖平，译. 上海：华东师范大学出版社，2017.

[2]章建跃. 数学学科核心素养导向的“单元—课时”教学设计[J]. 中学数学教学参考（上旬），2020（5）：5-12.

[3]章建跃. 数学学科核心素养导向的“单元—课时”教学设计（续）[J]. 中学数学教学参考（上旬），2020（6）：6-12.

[4]孙元勋.“函数的基本性质”单元—课时教学设计[J]. 中小学数学（高中版），2020（1）：1-5.

[5]刘国祥，姚为荣. 数学“大概念”视角下的单元教学设计：以“向量的概念及其运算”为例[J]. 高中数学教与学，2020（8）：1-4.

[6]刘薇，徐玲玲.“大概念”和“大概念”教学[J]. 上海教育，2020（4）：28-33.

[7]侯宝坤. 研读向量基本定理，构造创新试题[J]. 数学通讯（下半月），2017（3）：58-60.