基于SOLO分类理论的数学运算分析与思考

张阳

摘  要：数学运算素养是指在明晰运算对象的基础上依据运算法则解决数学问题的素养. 根据SOLO分类理论运算等级，2020年全国新高考Ⅰ卷中的所有试题均可以按照四种层次进行分析，不同层次的数学运算源于学生对问题的表征差异，而学生的学科素养水平直接影响其表征能力. 在教学中，教师需要从课程标准演进中解读数学运算，在数学学科核心素养中理解数学运算，依据系统论原则培养学生的数学运算素养.

关键词：新高考;数学运算;表征;系统;流程图

数学运算是指在明晰运算对象的基础上依据运算法则解决数学问题的素养. 数学运算包括算理与算法两个部分：算理指数学运算规则，如四则运算、代数式运算法则、方程与不等式的恒等变换、三角恒等变换、矩阵运算等;算法指数学运算的方案与程序，是在算理自觉运用的前提下，与所学内容高度融合，形成某个特定问题的解题思维方法，是学生创新意识与综合能力的体现.

数学运算考查的内容主要集中在掌握运算法则、设计运算程序两个部分. 前者强调算理，后者体现算法.

一、基于SOLO分类理论的数学运算分析

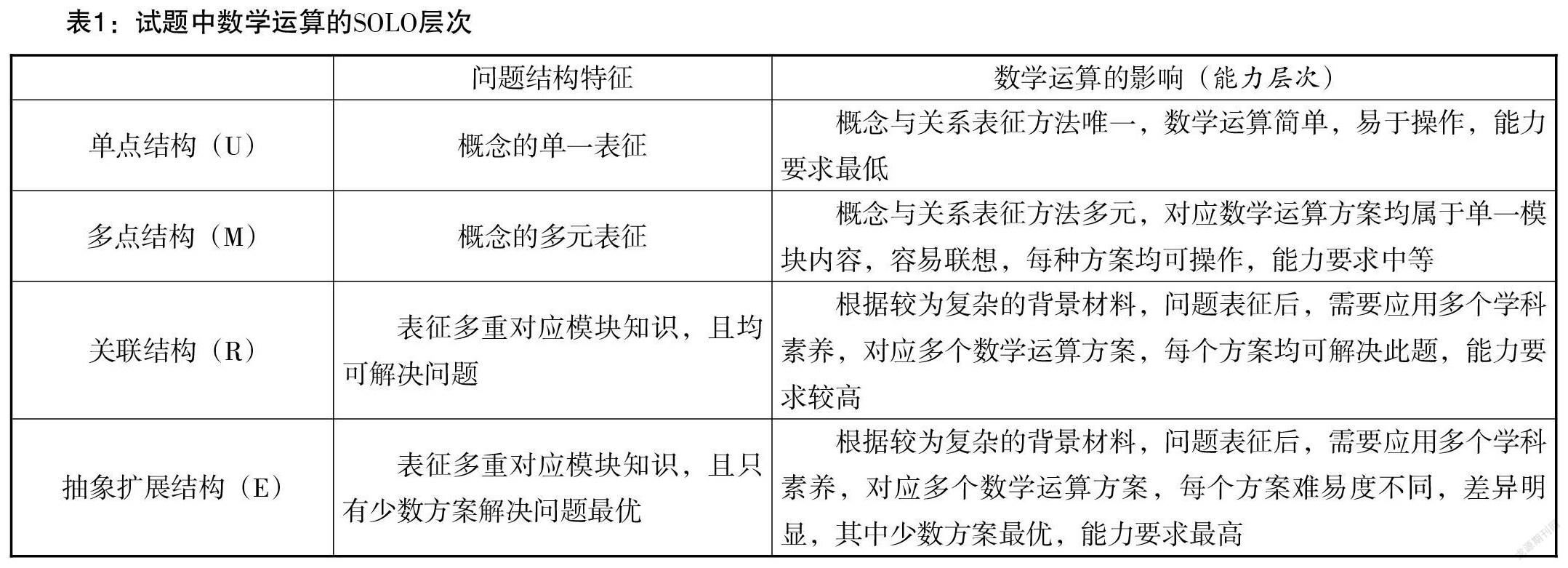
以2020年全国新高考Ⅰ卷为例，对基于SOLO分类理论的数学运算进行分析. SOLO分类理论是以等级划分的形式来描述学生思维能力目标，从而评价学生学习质量的一种“质性评价”方法. 按照这一分类理论将数学运算进行层次划分，如表1所示.

2020年全国新高考Ⅰ卷共22道题，除了第20题立体几何题第（1）小题可以用逻辑推理进行证明外（考查线面垂直关系的证明，也可以通过建立空间直角坐标系，利用向量计算的方法进行证明），其余各题都需要进行数学运算.

可以看出，数学运算是高考数学的考查重点，作为数学学科核心素养之一，与其他数学核心素养相互联结，共同为解题服务.

1. 概念引发单一表征，考查数学运算规则（单点结构U）

问题中的概念理解没有难度，其表征形式单一，解题路径唯一，仅考查数学运算中学生的算理能力. 在解题时，学生没有歧义，方法选择及运算均没有困难.

【评析】问题表征对象单一，目标明确，考查学生复数的运算法则，易于操作，难度低.

2. 概念引发多元表征，形成不同运算路径（多点结构M）

低难度的数学题考查学生对数学基本概念、基础知识、基本方法等数学知识的掌握情况. 此类问题的特点是概念本身引发的多元表征，学生通过表征数学问题（表征世界），映射所掌握的内在知识（被表征世界），形成解题路径，不同的解题路径对应着不同的运算路径，从而解决问题.

【评析】数学问题的表征形式相对固定，它将作为外部世界的现实问题，加工成图象、图表、表格、符号、动作、语言等初步存储到学生的大脑，此时学生的大脑对表征结果进行了抽象化处理，主要包括数量、关系等. 表征结果与学生认知体系的对应产生了不同的解题路径. 该题方案1，表征结果与学生认知体系中的立体几何产生了对应，侧重于逻辑推理的数学运算;方案2则是解析几何与之产生对应，侧重于方程的数学运算. 因此，该题更多的是考查学生对运算方案的选择.

4. 数学学科素养水平，映射运算方案优化程度（抽象扩展结构E）

对于较为复杂的背景材料，学生要整合多个数学学科素养，对问题进行推理与演绎，通过分析条件和条件间的联系，寻找不同的解题方案，进行试验，在试验中往往会出现阻碍与不畅的现象，需要学生不断地调试、优化，最终确定最优方案. 本质是程序设计优化的过程.

【评析】该题的两种方案都有依据，属于表征后的合理联想，但是在数学运算中算法（即运算的程序）优化是解决问题的重要因素，所以数学运算不单是计算能力，也是思维水平的体现，它的高效快捷依赖于逻辑推理、直观想象、数学建模、数学抽象、数据分析的综合应用，是学科素养的整合结果. 学生的数学学科素养水平高低，映射运算方案优化程度不同.

二、关于数学运算的教学思考

数学是研究数学关系和空间形式的一门科学. 数学教育承载着立德树人根本任务及发展素质教育的功能. 培养学生用数学眼光观察世界，用数学思维分析世界，用数学语言描述世界，教师对数学运算的理解直接影响教学的效果与目标的达成.

1. 从我国课程标准演进中解读数学运算

中学数学课程标准前后经历过四次系统变化，见表2.

从表2可以看出数学运算一直是课程标准的重要组成部分，但是数学运算的内涵却发生了一定的变化，在1952年与1963年的课程标准中用计算能力来理解数学运算，即强调了数学运算中的算理部分，要求学生精通算理、准确计算;2003年的课程标准中用运算求解能力对应数学运算，其背景是随着计算机的普及，烦琐的计算可以由计算机部分替代，教材內容随之发生变化. 例如，开根、对数表等内容均从教材中去除. 但是此时仍强调运算求解，对算理的要求大于对算法的要求. 2017年的课程标准则明确将数学运算作为数学学科核心素养之一，其背景是人工智能与大数据时代的到来，对运算方案提出了更高的要求，要求学生能设计算法程序，优化算法过程.

在课程标准的演进中，不难看出，数学运算从数学运算的重计算（算理）发展为重方案（算法）、重程序.

2. 在数学学科核心素养中理解数学运算

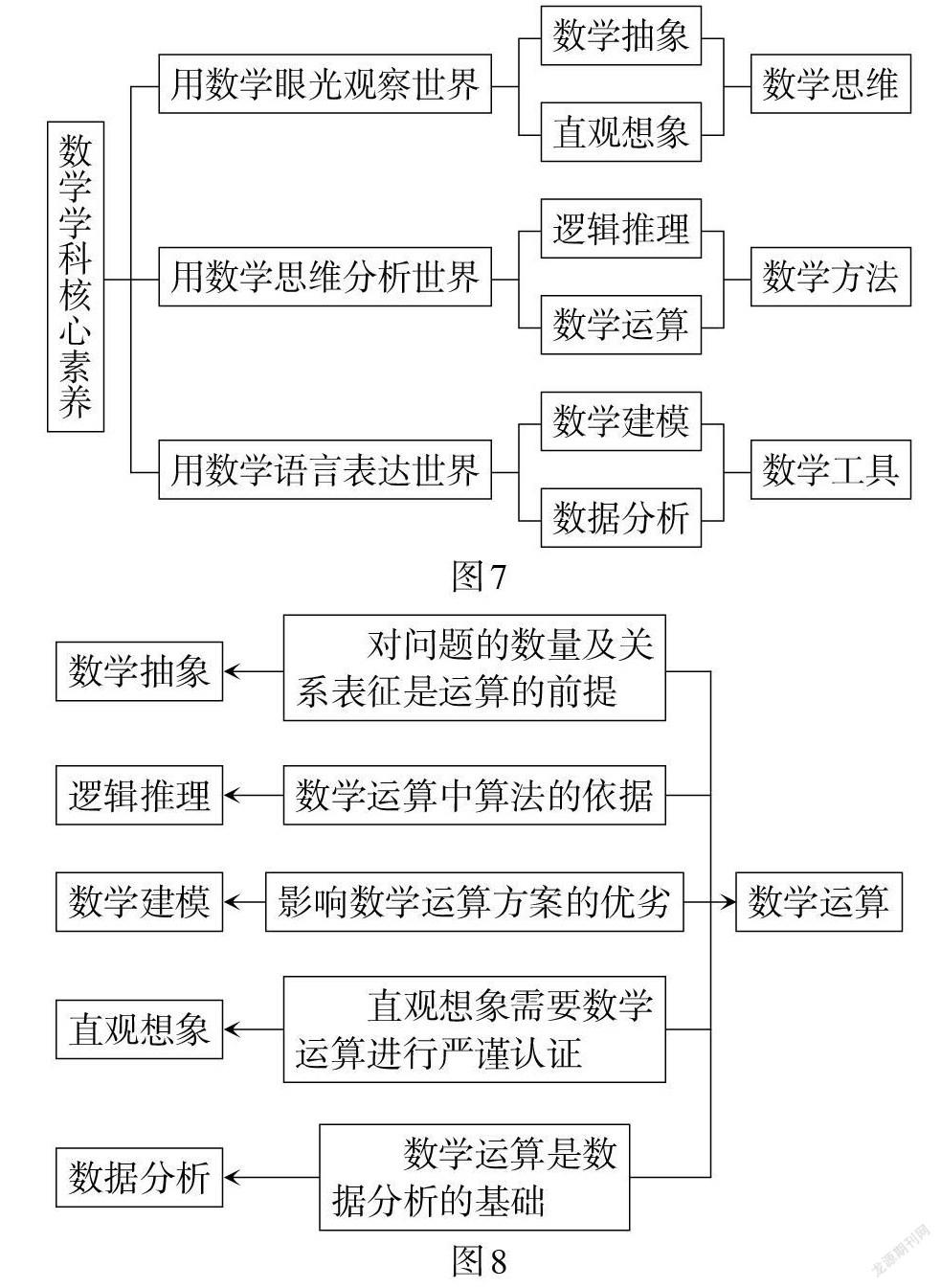
数学运算是数学学科核心素养的重要组成部分，它的合理使用离不开其他五大核心素养的支撑，六大核心素养之间是相互渗透的，如数据分析与数学运算. 数学学科核心素养在解决问题中的作用，如图7所示，数学运算与其他核心素养之间的关系，如图8所示.

数学运算在六大核心素养中往往起到联结作用，因为它们彼此间的影响强弱不同，但总体上相互关联，所以在课堂教学中培养数学运算素养需要全面培养学生的数学学科核心素养.

3. 依据系统论原则培养学生的数学运算素养

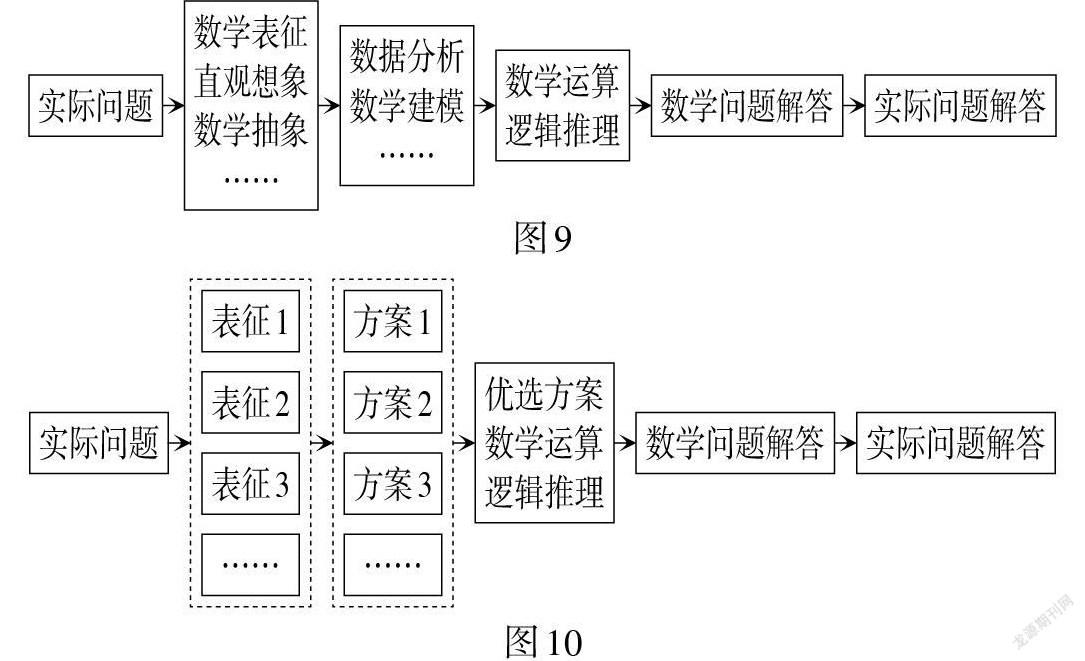
系统论认为，系统是由相互作用和相互依赖的若干组成部分，结合成具有特定功能的有机整体. 一切事物、现象和过程均可看作有机整体，成为系统. 在系统中，数学运算可以看作课堂教学的目标系统之一，也可以看作问题解决系统中的一环. 依据此理论，常见的解题流程图有循环结构（如图9）和顺序结构（如图10）.

循环结构的特点是重复表征、建模、推理、运算等过程，每一次都是在预设顺利进行的情况下推进，当受阻时即重复解题过程. 而顺序结构则是对实际问题进行多元表征，由表征结果进行多种方案预设，再优选方案，进行运算推理，得到数学问题的解答，再回归实际问题结论. 两种结构在解决问题时优劣与问题的难度有关. 基于SOLO理论对数学问题进行分类，其中单点结构（U）与多点结构（M）选用循环结构较适用，而对于关联结构（R）与抽象扩展结构（E）则顺序结构效率更高. 在数学教学中，应让学生有意识地体验两种解题流程，感悟核心素养在数学解题全流程中的应用，特别是顺序结构中的表征活动与方案设计，应该作为教学的重点内容.

参考文献：

[1]中华人民共和国教育部制定. 普通高中数学课程标准（2017年版）[M]. 北京：人民教育出版社，2018.

[2]中华人民共和国教育部制订. 普通高中数学课程标准（实验）[M]. 北京：人民教育出版社，2013.

[3]钟丽纯. 基于SOLO分类理论的高考试题能力结构研究[J]. 地理教学，2018（12）：43-45.

[4]何克抗，郑永柏，谢幼如. 教学系统设计[M]. 北京：北京师范大学出版社，2002.