Theory of adaptive mechanical drive

K.S.Ivanov

Almaty University of Power Engineering and Telecommunication, Almaty, 050013, Kazakhstan

ABSTRACT A kinematic chain with two degrees of freedom and one input can have definability of motion only if there is an additional constraint of forces and velocities.Such a chain is a mechanism that has the brand new property of force adaptation.The article presents a kinematic and force analysis of two-mobile adaptive mechanisms and describes the principle of definability of motion.

Keywords:Two-mobile mechanism Definability of motion Force-speed constraint

The object of research is a kinematic chain with two degrees of freedom with one input and one output.Such chain can be the basis for creating an automatic transmission (CVT).

Currently,CVT is widely used as an automatic transmission,combining a hydrodynamic converter and a step gear box [1] .The disadvantage of the transmission is the complex design,which contains a torque converter,a step gearbox and a step control system.

Recently,attempts have been made to use a two-mobile kinematic chain to create a stepless transmission.Crockett [2] and Volkov [3] used a hydrodynamic converter in combination with a multi-link differential gear train.Gulia [4] proposed a multilink friction variator with centrifugal control.Harris [5] and Vedeneev [6] presented a planetary mechanism without a hydraulic converter.The main goal of the researchers is to create a compact,simple,stepless CVT with a wide control range and high efficiency.However,the proposed designs have complex schemes and low reliability.

Recently,adaptive systems have been widely used in robotics,in autonomous transport technology and in the aerospace industry.However,little attention is paid to this topic in the academic and technical literature.Vaines presented a set of basic principles,engineering frameworks and adaptation applications in softwareintensive systems [7] .In his opinion,adaptation will be a crucial contributing function in solving the problems of new automatic executive systems.

Bollinger presented an overview of automated drives and controls in the context of a wide variety of industrial and laboratory applications [8] .It is stated that a multi-axis robotic device is a highly sophisticated machine that can have The insuperable theoretical control problems.

The adaptability can be significantly improved by using adaptive mechanical drives that independently adapt to the external load and do not require control of the power parameters.The control of such adaptive drives will consist only in the coordination of their actions.

The author,based on the combination of a kinematic chain with a movable closed contour and an additional force-speed constraint,developed a theoretical justification for the possibility of creating a stepless transmission with a wide range of control [9,10].A twomobile kinematic chain with a closed contour and an additional constraint allows you to create a mechanism with two degrees of freedom which has the property of force adaptation.However,the developed theoretical justification based on the principle of virtual works was not performed correctly enough which reduces the level of reliability of the performed studies.

In this paper,we use a research method that fully corresponds to the object of the study.In this paper,it is assumed that the two-mobile mechanism is able to exist in the mode of steady motion with equal work at the input and output.For this object,it is necessary to perform studies that ensure the definability of motion when there is only one input.The existing method of studying a kinematic chain with two inputs using the principle of possible displacements [11] does not correspond to the object under consideration.Therefore,a new formulation of the research problem is proposed:to ensure the definability of the motion of a two-mobile kinematic chain by introducing an additional constraint and to develop conditions for the relationship of the mechanism parameters for the steady-state motion mode.The relationship between the parameters is provided by the conditions of static equilibrium and the law of conservation of energy.The additional constraint in the object under consideration must comply with the law of conservation of energy.To do this,it must link forces and velocities(force-velocity constraint).

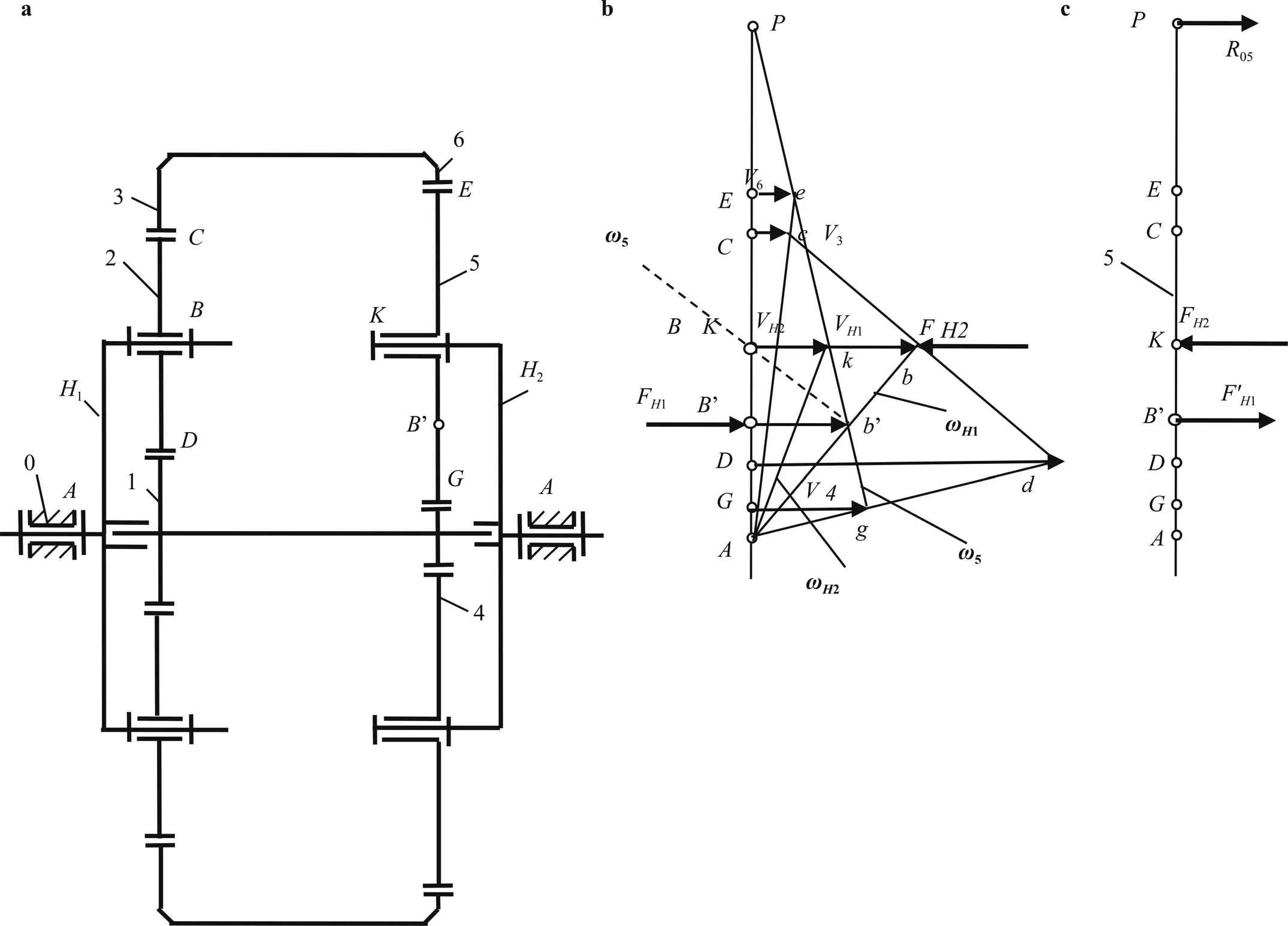
Fig.1.a Kinematic chain of the mechanism with two degrees of freedom, b the plan of linear velocities of the chain and c link 5 with applied forces.

The article presents the basics of the theory of mechanisms with two degrees of freedom with one input.The kinematic and force analysis of two-mobile adaptive mechanisms is developed and the principle of motion definability is described which allows to implement an additional constraint with a sufficiently high effi-ciency.

The kinematic chain of a fundamentally new mechanism with two degrees of freedom and one input (Fig.1a) contains a rack 0,an input carrierH1,a movable closed contour with gears 1-2-3-6-5-4 and an output carrierH2.A closed contour having zero mobility contains a satellite 2,a solar wheel block 1-4,a ring wheel block 3-6,and a satellite 5.The carriersH1 andH2are the initial links of the mechanism.The initial links can have set angular velocityωH1 andωH2and the corresponding moments of forcesMH1andMH2.The momentMH1=const,the momentMH2can take different values within a given range.

Linear kinematic and force parameters:

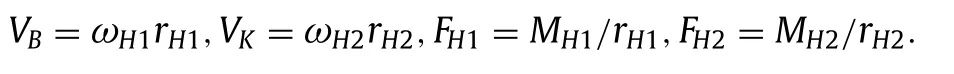
HererH1,rH2are the radii of the pointsB,Kof application of forces.

The presented two-mobile scheme of the mechanism with a movable closed contour allows you to build a plan of linear speeds according to the set speeds of the two initial links (Fig.1b) and bring the acting forces to the intermediate link 5 (Fig.1c).

Presented in Fig.1a the scheme of a two-mobile mechanism with a movable closed contour allows you to create equilibrium conditions.(In a mechanism with two degrees of freedom,it is impossible to create equilibrium conditions without a closed contour).The equilibrium of the system leads to the implementation of the law of conservation of energy in the mode of steady motion.

Closed-contour theorem 1

A kinematic chain with two degrees of freedom,containing an input link,an output link,and a movable closed chain placed between them,can exist in a steady-state mode of motion.

For the scheme (Fig.1a),it is necessary to prove that the work(or power) on the input linkH1is equal to the work (power) on the output linkH2,that is,

We will assume that with the steady motion of the system in the form of a gear planetary mechanism,all the links move uniformly,and there are no inertia forces.

To prove the theorem,we transfer all the acting forces to satellite 5 (Fig.1c).A movable closed contour allows you to perform this transfer.

According to Fig.1a the forceFH1=MH1/rH1acting at the pointBis transmitted to the link 5 from the carrierH1to the satellite 2 through the wheel blocks 3–6 and 1–4 in the form of reactionsR65=0.5FH1r3/r6andR45=0.5FH1r1/r4.The input force reduced to link 5 is equal to the sum of these reactions=0.5FH1(r3r4+r1r6)/r4r6.Hereriis the radius of the wheeli.

The position of the point of applicationBof the reduced forceis determined by the formulaKB=r5(r1−r4)/r4.Reduction of forceto a link 5 corresponds to the condition of equality the power of these forcesThe forceis applied at the pointK.

Next,consider the equilibrium of link 5 (Fig.1c).The sum of the moments relative to the instantaneous centerPof the link velocities is zero ∑MP=0.Or

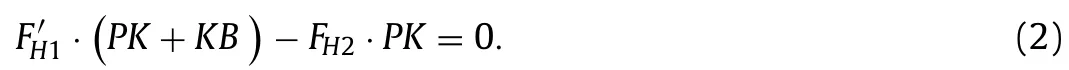
HereKB=eis the eccentricity.From here,the position of the instantaneous velocity centerP(distancePK) can be determined through the given forces.

Taking into account the motion of link 5 around a pointPwith an angular velocityω5,you can use the substitutions in Eq.(2)

Substituting the values of the velocitiesVB=ωH1rH1,VK=ωH2rH2into this equation,we obtain the equation of equilibrium of the entire mechanism according to the law of conservation of energy

quod Erat demonstrandum.

At the same time,Eq.(4) corresponds to the principle of virtual work (capacity) but with a significant difference–using real speeds instead of virtual ones.

From Eq.(4) follows the expression of force adaptation

At a given constant input power on the linkH1the output angular velocityωH2adapts to the variable output resistance torqueMH2.

Thus,a movable closed chain in a two-mobile kinematic chain with one input and one output creates the possibility of force adaptation.

Equation (4) of the equilibrium of link 5 and the entire system corresponds to the principle of virtual work (capacity) using real displacements (speeds).A valid displacement is one of the virtual ones.It can be assumed that the equilibrium Eq.(4) proves the definability of the motion of the system according to the principle of virtual works.However,for the equilibrium of link 5,it is not enough to use only the condition Eq.(1) that the sum of moments is equal to zero.In the general case,whenFH2>FH1,at the instantaneous center of the velocitiesP,a forceR05=FH2−FH1will appear a conditional (not really existing) reaction from the rack.This force does not participate in the equilibrium condition according to the virtual work principle Eq.(4),since the velocity of its point of applicationPis zero.In the case under consideration,Eq.(4) is not a necessary and sufficient condition for equilibrium.Link 5 cannot start moving in the absence of a real forceR05.

For the definability of motion at a pointP,it is necessary to create a real constraint,but this will contradict the possibility of creating an adaptation (the presence of two degrees of freedom).Definability of motion and the equilibrium can take place when forceR05 is taken into account only.

To ensure the definability of motion it is necessary to replace the action of a force with the action of another force,which creates an appropriate additional constraint in the equilibrium Eq.(4).This additional constraint should connect the moment to the angular velocity (or connect a force with a speed).

In the technique the constraint of the moment with the angular velocity is known -this constraint takes place between the moving links of the hydro-transformer and is determined by its characteristic.A similar constraint takes place between the links of the friction clutch.In the consider case,it is possible to use the relationship of the friction momentMfKin the hingeKof the satellite 5 with the angular velocity of the satellite relative to the output carrierω5 −H2=ω5−ωH2.In Eq.(4) this constraint will be included in the form of power consumed by friction in the hingePfK=MfKω5−H2.

Theorem 2 on the definability of motion

The definability of motion of a kinematic chain with two degrees of freedom can be provided by an additional mobile-limiting constraint of force with speed (or moment with angular velocity)as a function of powerPfK=MfKω5−H2included in the equilibrium equation.

For proof consider the equilibrium of link 5 (Fig.1c).The forceR05is determined from the second condition of the link 5 equilibrium–the sum of the forces is zero ∑F=0.From this condition

The definability of the motion of a two-mobile system can be achieved by replacing the momentM05of this unbalanced forceR05relative to the pointK(which is stationary at the start) with the friction momentMfKin the satellite hingeK.

The replacement (balancing) moment of frictionMfK=M05=R05·PK.

After substituting the valueR05from Eq.(6),we getMfK=(FH2−FH1)·PK.At a constant value of the input force the required friction moment depends on the output resistance forceFH2.

It should be noted that the moment of friction will require the input power to overcome the friction in the hingeKof the mechanismPfK=M05ω5−H2,whereω5−H2=ω5−ωH2.This power must be included in Eq.(4) of the equilibrium of the entire mechanism according to the law of conservation of energy:

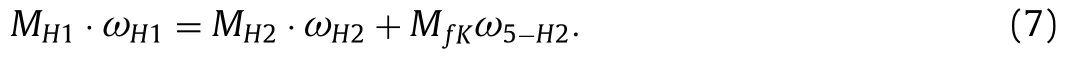
The introduction of the expressionPfK=M05ω5 −H2into the equation of the relationship of the parameters Eq.(4) corresponds to the introduction of an additional constraint that ensures the definability of motion.

Thus,the definability of motion of a kinematic chain with two degrees of freedom can be provided by an additional mobilelimiting constraint of force with speed (or moment with angular velocity) as a function of powerPfK=MfKω5 −H2included in the equilibrium equation,quod erat demonstrandum.

The geometry of the hingeKprovides the required value of the friction moment

Hereρ-the radius of the journal,f-the coefficient of friction,RH2−5=FH2-the reaction in the hingeK.According to Eq.(8) the required friction moment can be constantMfK=but the dependence on the reaction in the hingeKmakes it variableMfK=ρ fFH2.

From the Eq.(8) follows

To overcome the maximum resistance at the start the radius of the journalρmust be determined by the maximum value of the resistance forceFH2.A subsequent reduction in the resistance forceFH2 will result in a corresponding reduction in the required friction moment.

From the Eq.(7) we get the efficiency value as the ratio of the useful power to the total spent

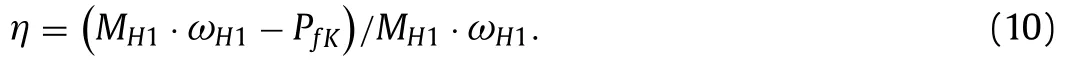
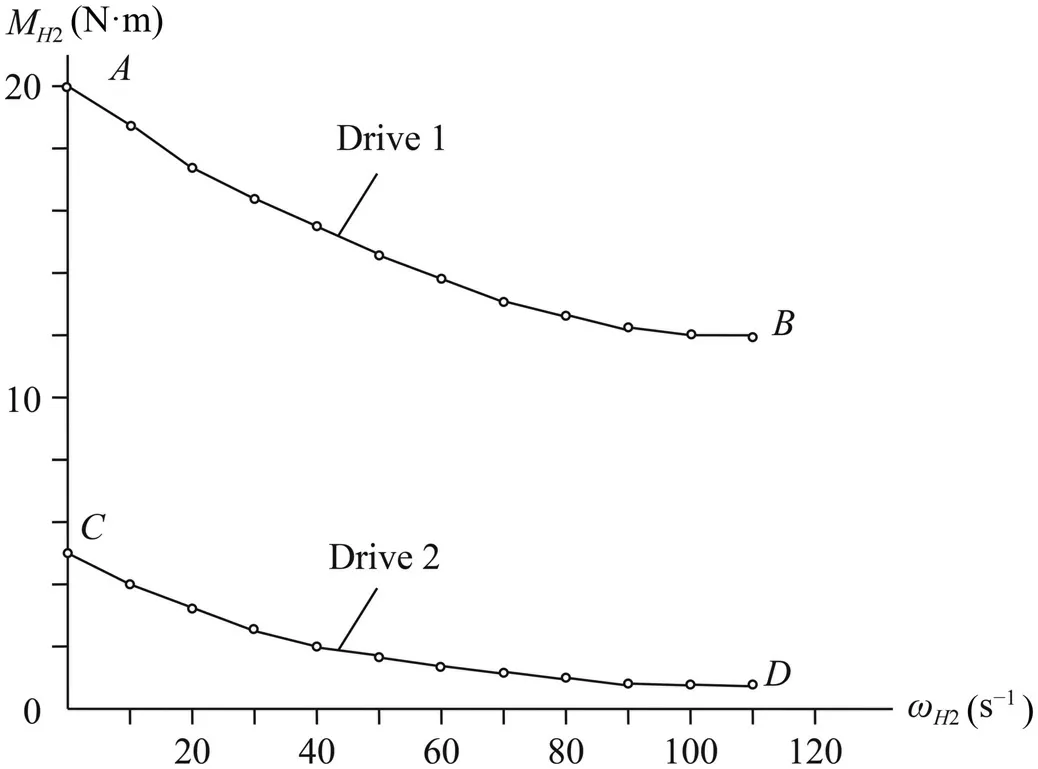
Fig.2.Comparison of the traction characteristics of the drive 1 with a balancing friction coupling and the drive 2 without a balancing coupling.

At the start (when starting from the place) we can acceptPfK=0.4MH1ωH1.The start is performed without using the clutch.We haveη=0.6.

On direct transmission (atωH2=ωH1)PfK=0.We haveη=1.

The use of a movable-limiting constraint with a balancing moment of friction in the hingeK(Fig.1b) will provide a wide range of control at a low relative speed of the links.The angular velocity lineω5can rotate under the action of the resistance forceFH2from the position providingωH2=0 (shown by the dotted line)untilωH2=ωH1,when the dotted line coincides with the lineωH1.Thus,the range of gear ratios of the mechanismuH1 −H2=ωH1/ωH2will be within 1 ≤uH1−H2≤∞.

The main task of the adaptive drive is to overcome a given variable moment of resistance corresponding to the output angular velocity.Let’s compare the two drives according to the criterion of overcoming the output moment of resistance.For comparison,we construct the traction characteristics of the drives as a function of the variable output moment of resistance from the output angular velocityMH2=MH2(ωH2).

Traction characteristics (Fig.2) are calculated using the specified power and kinematic parameters of the drive.

The input motor has constant parameters of powerPH1=MH1ωH1=10× 150=1500W.The output angular velocity will be set in the range 0 ≤ωH2≤110s−1with an interval 10s−1.

According to the given initial parameters,we will determine the kinematic parameters according to the known formulas of the kinematics of a planetary mechanism with two degrees of freedom[9] and the overcome moments of resistance in the presence of a balancing frictional moment.

For the drive 1 with a counterbalancing friction coupling,the output moment of resistance corresponds to the Eq.(7) and is expressed by the formula

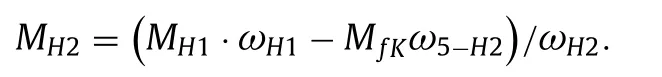
For the drive 2 without a balancing link,the traction characteristic is expressed by the formulaMH2=MH1·ωH1/ωH2.This dependency does not provide reliable operation in a mechanism with perfect connections.Even if there is a minimum moment of resistance,the output shaft stops,and the mechanism enters a state with one degree of freedom.In practice,the connections in the mechanism are not perfect.Friction power losses occurPf≈0.1MH1ωH1.This friction to a certain extent replaces the required calculated balancing moment of friction and allows overcoming the reduced moment of resistance (for example,in the presence of dry friction).The mechanism will overcome the variable moment of resistance,but within limited limits according to the formula

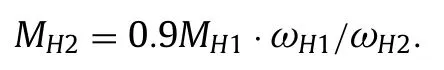
It should be noted that the drive 2 will use only a part of the rated power of the engine,corresponding to the actual power consumed by friction.

For the drive 1 (Fig.2),the motor power is equal toPH1=MH1ωH1=10× 150=1500 W.The starting point of the traction characteristicAon the ordinate axis corresponds to the following parameters:

The end point of the traction characteristicBcorresponds to the following parameters:

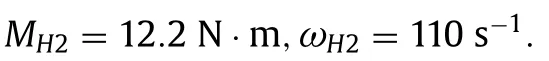
For the drive 2,the power consumption of the motor to overcome a relatively small moment of resistance will be equal

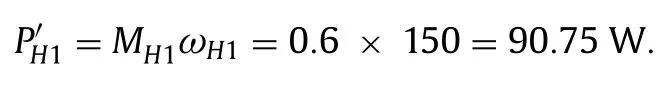
The small motor torque is used to overcome the corresponding drag torque.

The starting point of the traction characteristicCon the ordinate axis corresponds to the following parameters:

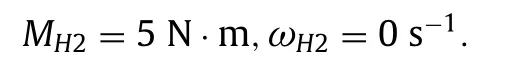
The end point of the traction characteristicDcorresponds to the following parameters:

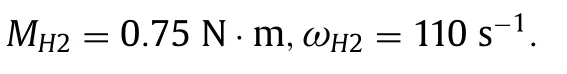
The traction characteristics of the drive 1 and drive 2 are shown in Fig.2.

Thus,the drive 1 overcomes the variable output moment of resistance corresponding to the input power.Drive 1 provides motion definability and reliable operation in adaptive mode.

The drive 2 can overcome a significantly reduced output moment of resistance if there is friction in the drive connections.

The drive 2 can transfer considerably smaller power and does not provide definability of motion and reliability of work in an adaptation regime.

Theoretical results coincide with experimental data earlier gained for the drive 2 [10].

The performed research allows us to formulate the following general principles for creating definable mechanisms with two degrees of freedom and with one input:

1) The basis of a two-mobile mechanism is a kinematic chain with two degrees of freedom,having one input,one output and a movable closed chain placed between them.

2) The definability of the motion of the mechanism is provided by the mobile-limiting constraint of force and speed in the form of a friction hinge on the output satellite.

3) The mobile-limiting constraint is a fundamentally new type of force-speed constraint (or moment and angular velocity constraint).This constraint can be provided by a friction hinge.

4) A comparative analysis of the drive 1 with a balancing link and the drive 2 without such a link showed that the drive 1 provides the transmission of the calculated torque,and the drive 2 under the action of a similar resistance moment goes into a state with one degree of freedom-it turns out to be inoperable.The drive 2 can provide the transmission of a significantly reduced variable moment of resistance,corresponding to the friction losses in the mechanism.

The two-mobile mechanism with one input has a fundamentally new property of force adaptation.The absence of a control system in the drive greatly simplifies the design of the adaptive mechanism and increases its reliability.The adaptive mechanism has a wide range of gear ratios.The two-mobile mechanism has a relatively high efficiency due to the low power loss due to friction in the intermediate hinge.

The simplicity of the design,small dimensions and weight make the design of the mechanism competitive and suitable for use in the automotive industry,robotics,aerospace,and in mobile transport engineering.

The presented material defines the technology of creating fundamentally new adaptive mechanisms.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The research was supported by Grant No.AP09258712“Development of self-adjusting electric drives for spacecrafts”,planned at the Almaty University of Energy and Communication.