Electrothermal analysis of radiofrequency tissue ablation with injectable flexible electrodes considering bio-heat transfer

Min Hu ,Zhixiong Feng ,Yugung Chu ,Yuhng Li ,∗

a Institute of Solid Mechanics, Beihang University (BUAA), Beijing 100191, China

b Police dog base of Beijing Public Security Bureau, Beijing 102614, China

c Dept Cardiovasc, China Academy of Chinese Medical Sciences Guang’anmen Hospital, Beijing 100053, China

ABSTRACT Flexible electrodes have been widely focused on in recent years due to their special mechanical properties,which can be directly integrated onto human soft tissues to actively take effects on human body or passively monitor human vital signs.These flexible electrodes provide a new routine to realize clinical treatment of accurate thermal ablation in the biological tissues via radiofrequency ablation (RFA).Meanwhile,accurately controlling of thermal field is very significant for the thermal ablation in the clinical therapeutics to prevent the healthy tissue from excessive burning.In this paper,both one-dimensional and two-dimensional axisymmetric analytical models for the electrothermal analysis of radiofrequency ablation considering bio-heat transfer are established,which are verified by finite element analysis (FEA)and in vitro experiments on pig skins.In the model,the electrical field and thermal field are both derived analytically to accurately predict the temperature rise in the biological tissues.Furthermore,parameters,such as the blood flow convection in living tissues and thickness of tissue,have obvious effects on the thermal field in the tissues.They may pave the theoretical foundation and provide guidance of RFA with flexible electrodes in the future.

Keywords:Flexible electrods Radiofrequency ablation Electrothermal analysis

With excellent structural designs,including island-bridge designs [1],serpentine interconnects [2] and fractal-inspired designs[3],flexible electronics have made great progress in biomedical applications in recent years,such as cognitive monitoring,prosthetic control [4],wireless drug delivery [5,6] and so on.Due to excellent flexibility and stretchability,flexible electrodes have been applied in in-vivo surgical instruments [7,8],which can be directly integrated onto human soft tissues to actively take effects on human body or passively monitor human vital signs.These flexible electrodes provide a new routine to realize clinical treatment of accurate thermal ablation in the biological tissues via radiofrequency ablation (RFA) [9] .Ko et al.[10] has verified the similar efficacies of the flexible electrodes compared with the traditional electrode for laparoscopic radiofrequency ablation in the ex vivo study.In fact,it is vital to precisely control the range of lesion in the ablation therapy so that the whole diseased tissue can be completely destroyed without excessive damage to the normal tissue nearby.

Generally speaking,radiofrequency ablation destroys the diseased cells via heating them around the range of 50-60 °C,under which the protein denaturation will appear [11] .Due to the fact that the permeability of diseased cells is better than that of normal cells,the temperature changes more violently in diseased cells.However,the temperature in the surrounding cells must be controlled below 45 °C,where the thermal damage can be reversible.On the other hand,the temperature over 100 °C is strictly not allowed during the operation for avoiding charring and tissue microexplosions,which guarantees the patients’ safety [12] .

Aiming at accurately determining the ablation zone accurately,many researchers have made a series of work on the precise output control of the operated devices.Jensen et al.[13] developed a new controller with the near-deadbeat control method to reduce the lesion.In order to improve both flexibility and controlling accuracy,Jensen et al.[14] proposed a digitally controlled two-rail multiphase buck converter to shape the output ac waveform with different frequencies.Special attentions should be paid on that Koh et al.[15] designed a kind of ultrathin flexible sensor for radiofrequency ablation monitoring the temperature change in real time.

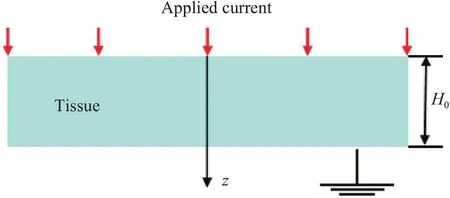
Fig.1.Schematic diagram of one-dimensional model for the biological tissues.

In addition to device improvement,accurate electrothermal modeling is another significant means to predict the temperature field in the biological tissues and protect the safety of human body.Haueisen et al.[16] discovered that low frequency alternating current (AC) voltage and direct current (DC) voltage have the same effect on the depth of the lesion,which verifies the practicability of quasi-static electrothermal model.Ciesielski et al.[17] focused on the mathematical modeling for the endoscopist control of the current flow with the size of the polyp.Kuroda et al.[18] developed an electrosurgical cutting simulation system containing a series of physical phase,whose results agreed well with the results obtained by the experiment of porcine liver.Wang et al.[19] established an image-based 3D modeling via a tissue-mimicking breast gel phantom and its magnetic resonance (MR) images to perform preoperative finite element analysis.

Fast and accurate predictions of temperature rise in biological tissue under radiofrequency ablation are in great demand.Therefore,to accurate prediction and control of the temperature rise in operation,both one-dimensional and two-dimensional axisymmetric analytical models are established in this paper combined with basic equations of constant electric field and bio-heat transfer equation which are in good agreement with simulation results and experimental results.

For the large area flexible electrodes,the effects of the electrodes can be neglected,which means that the electrical filed and thermal field in the biological tissues will vary only along the thickness direction but not with other directions.Another assumption is that the flexible electrode can be neglected in the analytical model because the thickness of the flexible electrode(around several hundred nanometers) is four-order less than that of biological tissues (around several millimeters).Therefore,the area covered by the flexible electrode can be simplified as a onedimensional model to derive the temperature rise in the biological tissues without considering the influence of the surrounding area.The schematic diagram of one-dimensional analytical model for the biological tissues with applied current is shown in Fig.1 with coordinate origin at the top surface and coordinatezalong the down direction.The thickness of the tissue is denoted byH0.For the electrical boundary conditions,there is an applied current at the top surface of the biological tissue and the zero potential is located at the bottom surface.While,for the thermal boundary conditions,there is a natural heat convection at the top surface and constant temperature rise at the bottom surface.

Firstly,the distribution of potential field in the biological tissue satisfies the law of conservation of electric charge,

whereϕis the electrical potential.For the electrical input,there is an applied current densityj0at the top surface of the biological tissue (z=0),

While,the bottom surface of the biological tissue is the ground electrode (z=H0),

With the conditions above,the solution for Eq.(1) can be obtained as following:

The electrical potential distribution obtained above is the heat generation of thermal field in the biological tissue and as a result,the Joule heating produced by electrical current can be expressed as

whereσis the electric conductivity of the biological tissue.The temperature of the biological tissueTsatisfies the Pennes bio-heat transfer equation [20],

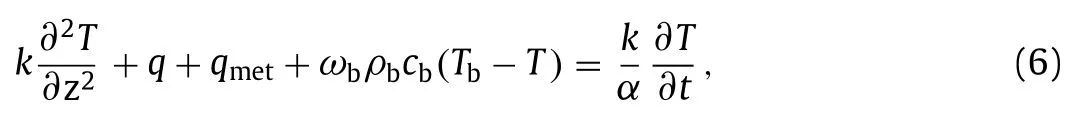
wherekandαare the thermal conductivity and thermal diffusivity,respectively.The termqmet stands for the heat generation from metabolic activities andωbρbcb(Tb–T) represents the heat transfer due to the local blood flow to tissue.ωb,ρb,cbare velocity,density and specific heat of blood in the biological tissues,respectively.Furthermore,the temperature rise is defined asθ=T–T∞and then

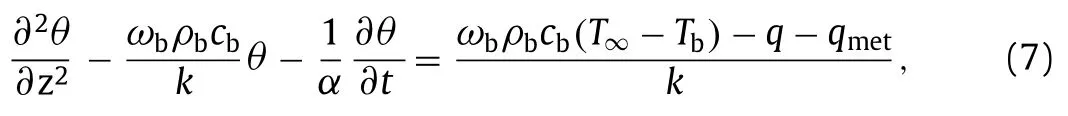
At the top surface of the tissue (z=0),forced convection of blood is considered,which gives

wherehbis the blood forced convection coefficient.T∞is the temperature of blood.Meanwhile,the temperature of the bottom surface (z=H0) is fixed to the body temperature,

Laplace transform is applied to the Eq.(7):

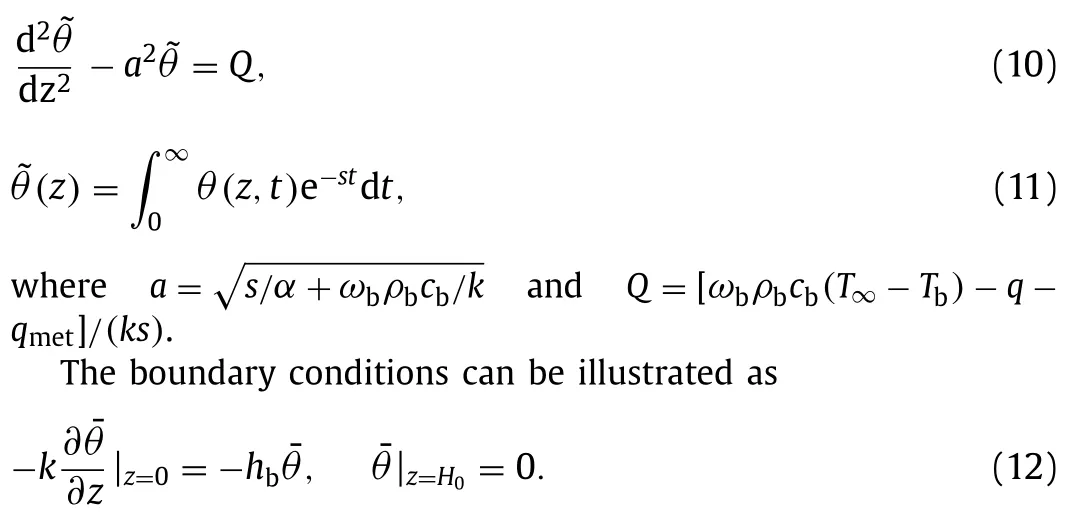
The Eqs.(4)–(6) and (10)–(12) are solved simultaneously as

whereC1andC2are coefficients that determined by definite conditions in Eq.(12) as

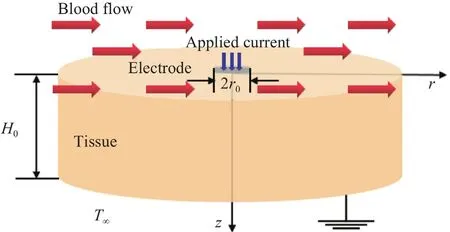
Fig.2.Schematic diagram of axisymmetric model.

The solution of temperature field is obtained by inverse Laplace transform:

The two-dimensional axisymmetric model is established as shown in Fig.2.The coordinate origin is set on the top surface of the tissue.ris the radial direction whilezstands for the depth of the tissue.The radius of the ablation electrode is denoted byr0 and the thickness of the tissue is denoted byH0.

The distribution of the potential fieldϕin the tissue satisfies the law of conservation of electric charge:

The boundary condition of the top surface is divided into two parts (z=0).

(1) There is input currentj0within electrode radius (–r0≤r≤r0):

(2) The normal current density outside the electrode radius is 0 (r>r0 orr<–r0):

And the bottom surface of the tissue is grounded (z=H0):

Hankel transform is applied toϕ:

Then Eq.(17) is transformed into:

Equations (18)–(20) can be written as

J1is first order Bessel function of the first kind.

Solve the Eqs.(22)–(24):

whereAandBare

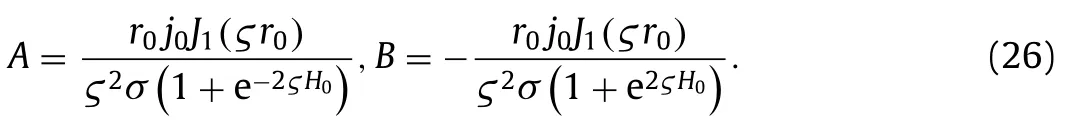
Therefore,the distribution of the potential is obtained by inverse Hankel transform:

J0is zeroth order Bessel function of the first kind.

Similarly,the Joule heating produced by electrical current can be expressed as

The temperature rise is defined asθ=T–T∞.The temperature rise of the tissueθsatisfies the Pennes bio-heat transfer equation,

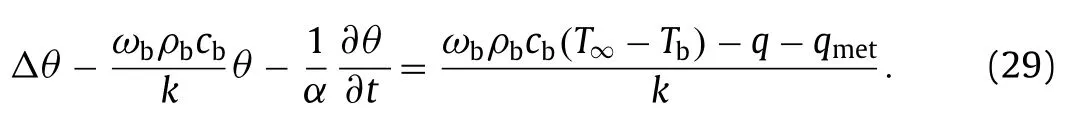
Laplace transform is applied to the Eq.(28):

whereλ=−ρbcbwb/kandf(r,z)=−q/k−ρbcbwb(Tb−T∞)/k−qmet/k.

Thermal boundary conditions are kept the same with the onedimensional model,which can be transformed accordingly as follows:

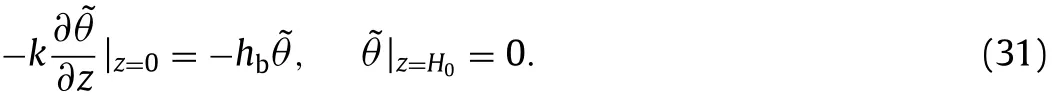
Hankel transform is applied to Eqs.(30) and (31),

The Eq.(32) is solved as follows,

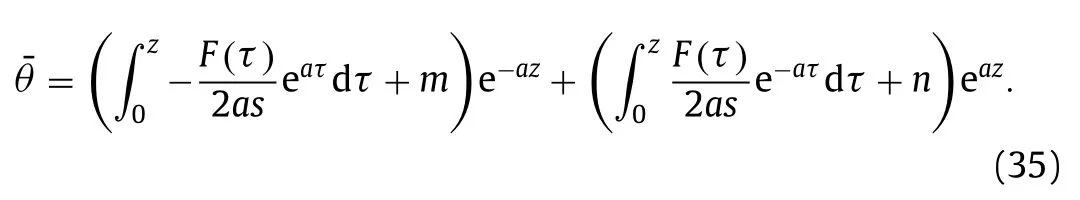
mandnare coefficients that determined by definite conditions in Eq.(33) as

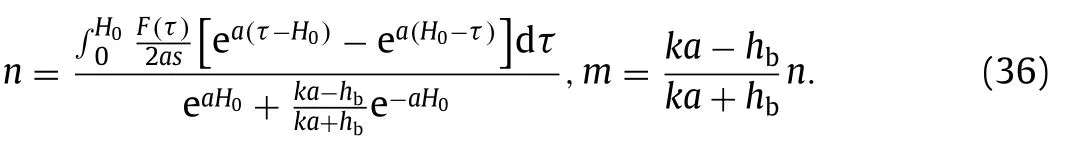
The solution of the temperature field is obtained by inverse Hankel transform and inverse Laplace transform,

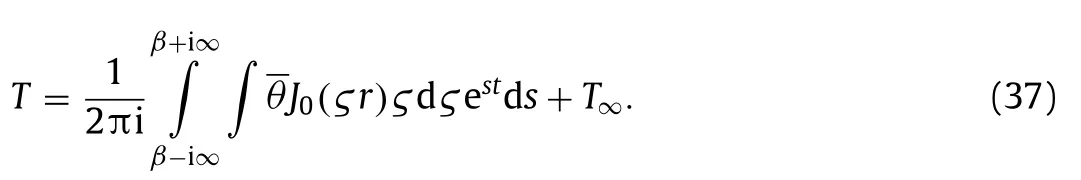
Fig.3.(a) Transient maximum temperature rise considering bio-heat transfer.(b) Steady-state temperature distribution along the depth considering bio-heat transfer.

To illustrate the results obtained by the analytical model,myocardial tissue is taken as a typical example.The electric conductivity of myocardial tissueσis set to be 0.35 S/m [21].The input currentj0 is 750 A/m2on the top surface while the bottom surface is grounded.The thermal conductivitykand the thermal diffusivityαof the tissue are 0.59 W/(m2•K) and 1.561× 10−7m2/s,respectively [22].The thickness of the tissue is set as 10 mm if not specified.Furthermore,the velocityωb,densityρband specific heatcb of blood are 0.005 ml/(ml•s),1050 kg/m3,3600 J/(kg•K),respectively.If not mentioned,the blood forced convection coeffi-cienthbis taken as 2089 W/(m2•K) [22].The metabolic heat productionqmet in myocardium is set as 368 W/m3[23].The blood temperature and the fixed body temperatureT∞are both kept at 37 °C as well as the initial temperature of the tissue.

Based on the parameters above,the transient temperature rise field in the myocardial tissue can be obtained analytically according to Eq.(37).Furthermore,a FEA model is established via COMSOL with multi-physical field adopted to verify the analytical model.In the finite element model,a regular quadrangular mesh is adopted to discretize the geometry with the grid size constrained in 0.01–0.1 mm,whose convergence has been checked.

The bio-heat transfer theory is considered in the proposed model to be closer to the reality.The Fig.3a and b illustrate that the bio-heat transfer theory cannot be ignored for the accurate temperature prediction.It can be found that the steadystate temperature with bio-heat transfer is lower than that without bio-heat transfer.The time required to reach the steady-state temperature is relatively short.In fact,bio-heat transfer is composed of blood perfusion and metabolic heat.The blood perfusion plays an important role while the value of metabolic heat is relatively small.If the bio-heat transfer is not considered in the operation,the input current will be too small resulting in the repeated operation.

Figure 4 shows the process of transient temperature rise at the point with maximum temperature rise with the thickness of 10 mm,15 mm and 20 mm,validated by FEA.The temperature rises rapidly at the beginning and then tends to be a stable value.With the increase of the tissue thickness,the steady state temperature rise increases.Furthermore,the required heating time to reach steady state increases with the thickness increasing from 10 mm to 20 mm.Figure 5 illustrates the spatial distribution of steady state temperature along the depth direction.In the figure,it can be found that the maximum temperature rise locates in the center region but not the top surface of the tissue because of the effects of the forced heat convection.

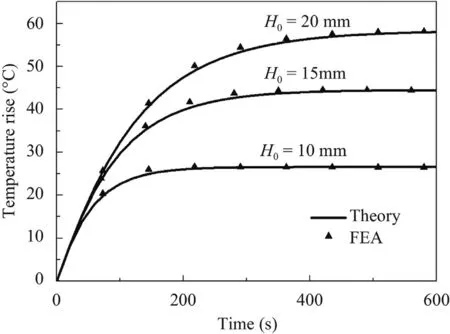
Fig.4.Transient maximum temperature rise with the input current of 750 A/m2.

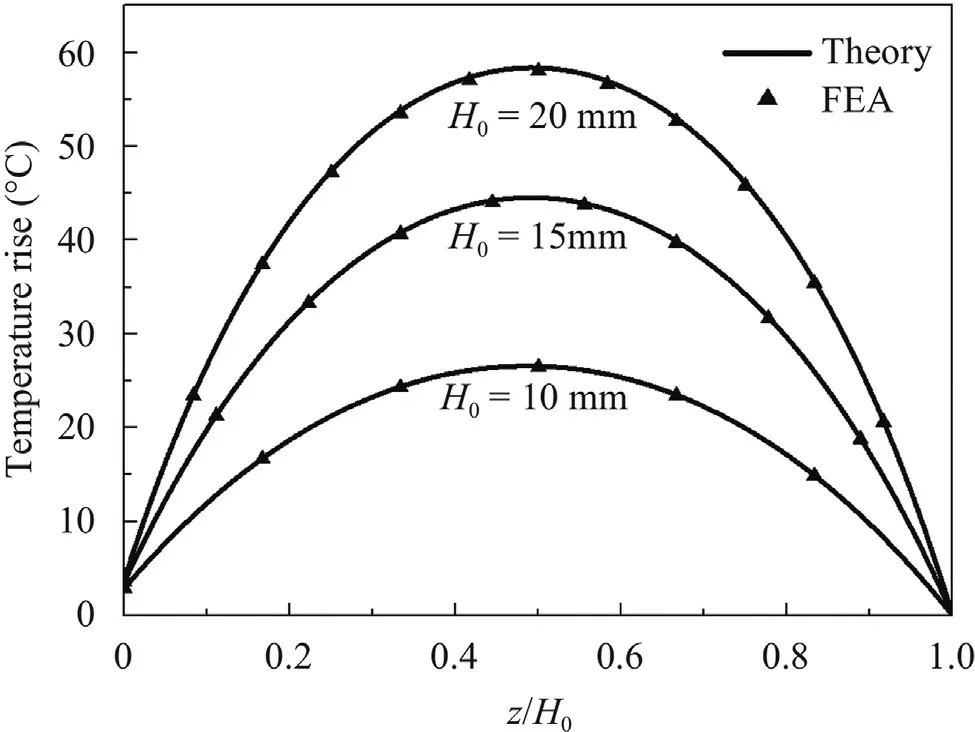
Fig.5.Steady-state temperature distribution along the depth.

To obtain the exact working time for RFA treatment apparatus,Fig.6 shows the heating time for reaching 90% of the steady-state temperature rise versus the thickness.As can be seen,the heating time increases with the tissue thickness varying from 10 mm to 20 mm,which can be a reference for surgery.

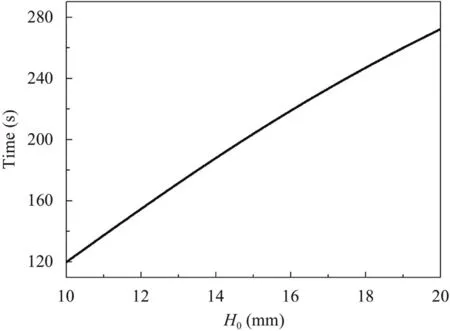
Fig.6.Time reaching 90% of the steady state temperature versus the thickness.

To verify whether the model is consistent with the reality,the electric heating experiments in vitro were conducted with the 1.8 mm thick pig skin.The platinum electrode with the radius of 1 mm was applied on the top surface of the skin while the ESUgrounding pad of aluminum was placed at the bottom.The current of 7 mA was provided for 100 s until the real-time temperature remained unchanged,which was recorded by VarioCAM HD (JENOPTIK;Jena,Germany).

Via COMSOL with multi-physical field,FEA was also performed to study the temperature distribution of the fresh pig skin.The current density could be calculated as 2229 A/m2and the electrical conductivity of the skin was 2.0 S/m [24].The thermal conductivity,specific heat capacity,and density are 0.37 W/(m•K),2846 J/(kg•K),and 1000 kg/m3[23].It is obvious that the bio-heat transfer was not under consideration in the experiment.Therefore,the convective heat transfer was between the skin and air instead of the blood,andhbis set as 8 W/(m2•K).The initial temperature of the pig skin and the air are both 25 °C.In the finite element model,over 171214 tetrahedral meshes are adopted to discretize the geometry with the grid size constrained in 0.01–0.1 mm whose convergence was checked.

The pig skin used in the experiment is displayed in Fig.7a and 7b.It is obvious that the lesion is more serious in the area covered by the electrode.Figure 8 shows the results of the temperature rise distribution along the radius on the surface of the skin.In general,the theory can match well with the experiment and FEA.Nevertheless,the consistency of the temperature rise within radius is not as good as that outside radius,which may result from the analytical model neglecting the thermal conductivity of the flexible electrode.

In order to better understand the thermal distribution of the axisymmetric model,the influences of different parameters have been researched.In the following study,the radius of the electrode is 1 mm while the input current densityj0 on the top surface is 10000 A/m2.The thickness is 10 mm and the blood forced convection coefficient is 2089 w/(m2•K) if not specified.The other parameters are kept the same as the one-dimensional model’s.

The potential distribution is displayed in Fig.9a and 9b with the theoretical and simulation results in good agreement.The potential is a spherically symmetrical distribution centered on the origin where the maximum potential is obtained.It can be found that the potential decreases rapidly to 0 V near the origin.According to the Eqs.(28) and (29),the potential gradient has the positive effect on the temperature rise verified by the results below.

Figure 10 shows the steady distribution of temperature rise along the depth direction whenris taken as 0 mm.Similar to the one-dimensional model’s results,the temperature rise firstly increases and then decreases while the maximum temperature rise point locates off the top surface.However,the change of the temperature rise is relatively sharp in the axisymmetric model with the point only 0.37 mm away from the top surface.

Distinguished from the one-dimensional model,it is necessary to discuss the distribution of temperature rise along the radius direction in the axisymmetric model,which is shown in Fig.11.Compared to the distribution along the depth direction,the trend is basically the same with different depth,declining with the increase of radius.It can be found that the temperature atz=0 mm andz=0.37 mm changes much more sharply,which leads to the lower temperature whereris 2 mm.

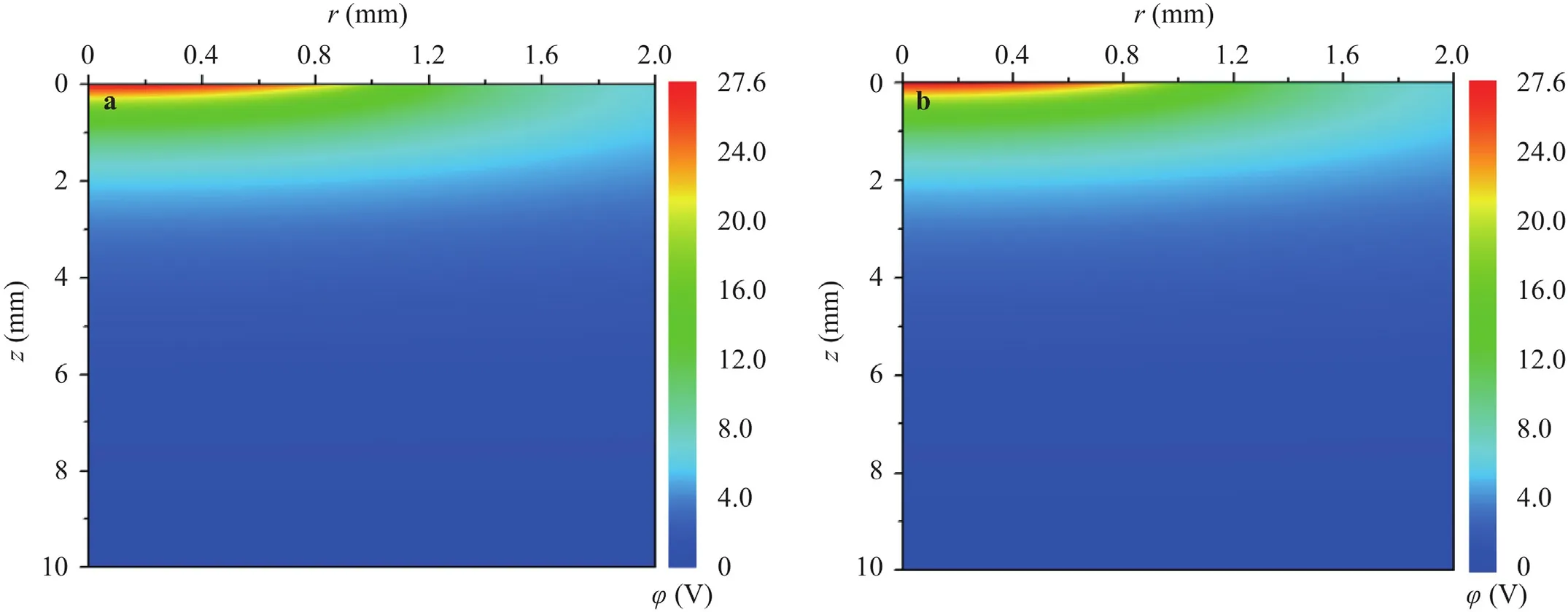
Fig.9.(a) Simulation potential distribution with 10000 A/m2;(b) theoretical potential distribution with 10000 A/m2.

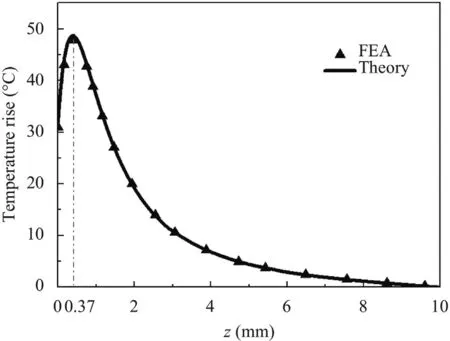
Fig.10.Steady-state temperature distribution along the depth in the axisymmetric model.

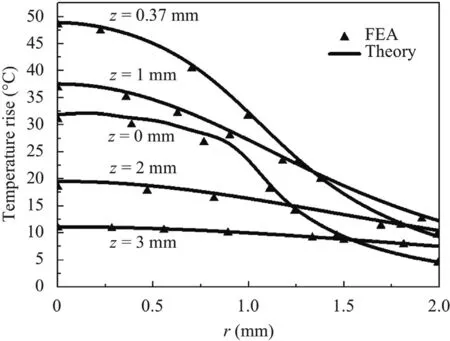
Fig.11.Steady-state temperature distribution along the radius versus the thickness.

Besides the steady-state thermal analysis,Fig.12a and b show the transient temperature rise at different points,both of which agree well.It can be found that the time reaching steady state increases with the increase of the depth wherer=0 mm.On the contrary,there is no significant difference in that of the different radius wherez=0 mm.

The influence of the blood forced convection coefficient on the maximum temperature rise is shown in Fig.13 since it varies with the blood velocity and the size of the heated vessel region.Through the three curves presented,namely 1208 W/(m2•K),1611 W/(m2•K) and 2089 W/(m2•K) [25],it can be obviously found that the increase of blood forced convection coefficient has the negative effect on the steady temperature while the required time simultaneously declines.This trend makes sense due to the fact that a larger blood forced convection coefficient means that more heat can be taken away in the same time,so as to reach a lower steady state faster.

Both one-dimensional and two-dimensional axisymmetric models are established to explore the thermal properties of the human tissue in RFA with flexible electrodes.The analytical solution for the transient temperature rise in the system is obtained via Hankel transform and Laplace transform,which is validated by finite element analysis and experiment.The influences of thickness and bio-heat transfer are investigated in the one-dimensional model.It can be found that the temperature in steady state and the time required to reach steady state will increase with the increase of thickness.In addition,bio-heat transfer obviously needs to be considered for accurate temperature prediction by comparison.In the axisymmetric model,the potential filed is of spherically symmetrical distribution centered on the origin.In the radial direction,the temperature rise reduces uniformly and the time reaching the steady state is similar.However,the temperature rise firstly increases sharply and then decreases while the required time becomes longer with the growing depth.Besides,the increase of blood forced convection coefficient leads to the decrease on the steady-state temperature.In the future,combined with preoperative diagnosis,the two analytical models can provide a theoretical basis for RFA with flexible electrodes to accurately control the input current avoiding excessive damage.The discussions of the parameters above may lead to an accurate prediction of temperature rise in the biological tissue so that the diseased tissue can be destroyed through only one operation.

Fig.12.(a) Transient temperature rise versus the depth where r=0 mm;(b) transient temperature rise versus the radius where z=0 mm.

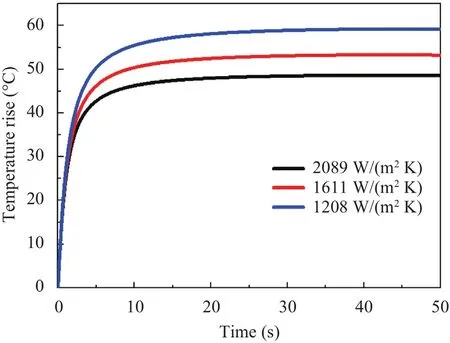
Fig.13.Transient maximum temperature rise versus the coefficient of forced convection.

Declaration of Competing Interest

We declare that we have no financial and personal relationships with other people or organizations that can inappropriately influence our work,there is no professional or other personal interest of any nature or kind in any product,service and/or company that could be construed as influencing the position presented in,or the review of,the manuscript entitled.

Acknowledgement

The authors acknowledge the supports from the National Natural Science Foundation of China (No.11772030) and the Aeronautical Science Foundation of China (No.2018ZC51030).