On the capability of the curvilinear immersed boundary method in predicting near-wall turbulence of turbulent channel flows

Fei Liao ,Xiaolei Yang

aState Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China

bSchool of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China

cSchool of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 10 0 049, China

ABSTRACT The immersed boundary method has been widely used for simulating flows over complex geometries.However,its accuracy in predicting the statistics of near-wall turbulence has not been fully tested.In this work,we evaluate the capability of the curvilinear immersed boundary (CURVIB) method in predicting near-wall velocity and pressure fluctuations in turbulent channel flows.Simulation results show that quantities including the time-averaged streamwise velocity,the rms (root-mean-square) of velocity fluctuations,the rms of vorticity fluctuations,the shear stresses,and the correlation coefficients of u ′ and v ′computed from the CURVIB simulations are in good agreement with those from the body-fitted simulations.More importantly,it is found that the time-averaged pressure,the rms and wavenumber-frequency spectra of pressure fluctuations computed using the CURVIB method agree well with the body-fitted results.

Key words:Immersed boundary method Turbulent channel flow Wavenumber-frequency spectra Near-wall turbulence

Turbulent flows in real-world applications often happen with complex geometry.The immersed boundary (IB) method,which is based on non-body-fitted grids,does not require complicated grid generation process,providing an efficient approach for simulating flows with complex boundaries.Although the immersed boundary method has been applied to different flow problems [1-4],its capability in simulating near-wall turbulence has not been systematically evaluated,which is of vital importance for some applications,e.g.,the noise prediction [5,6].The fractional step method is often employed for solving the incompressible flows [7-9] .When the immersed boundary method is employed with the fractional step method,the velocity reconstruction is often applied at the intermediate velocity instead of the final velocity after the projection step.This causes an inconsistency between the reconstructed velocity boundary condition and the divergence free condition.To address this problem,Kim et al.[10] introduced a source/sink term to the continuity equation for cells containing the immersed boundary.Ikeno and Kajishima [11] proposed a consistent scheme and examined the capability of the proposed scheme in predicting the mean velocity and velocity fluctuations for incompressible flows in aligned channel,inclined channel,circular pipe and nuclear rodbundle.In the work by Kang et al.[12],the reconstructed velocity is corrected using the least square method to satisfy the constraint of global mass conservation.The capability of the proposed approach was then assessed for predicting the mean streamwise velocity,rms (root-mean-square) of velocity fluctuations and wallpressure power spectra in turbulent channel flows.In this work,the curvilinear immersed boundary (CURVIB) method [8,13] is employed,which adopts a curvilinear grid as the background grid and allows approximately distributing grid nodes in a way following the immersed boundaries whenever it is possible.In the CURVIB approach,a correction term,which is often very small,is uniformly applied to the reconstructed velocity to ensure the global mass conservation.The objective of this work is to systematically examine the CURVIB method in predicting near-wall velocity and pressure fluctuations of the turbulent channel flow atReτ=uτδ/ν=180,whereuτis the friction velocity,δis the half height of the channel andνis the kinematic viscosity.

The virtual flow simulator (VFS) [14] is employed in this work for direct numerical simulation (DNS) of the fully developed turbulent channel flow.The governing equations are the threedimensional unsteady incompressible Navier-Stokes equations in curvilinear coordinates shown as follows:

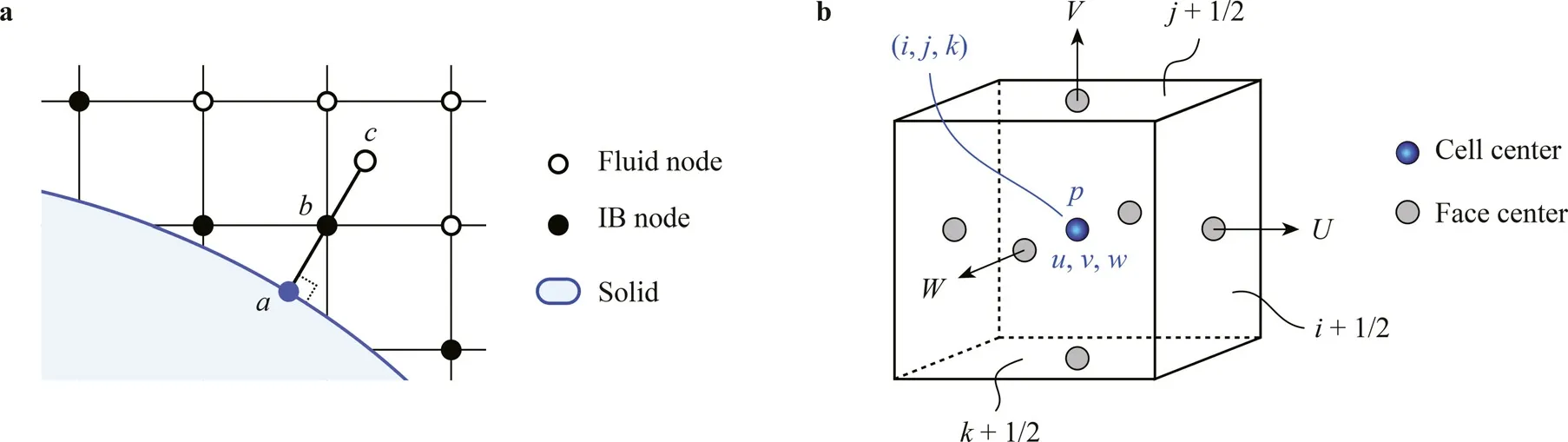
Fig.1.A schematic for a the reconstruction of the velocity at IB node and b the storage arrangement of velocity,pressure and contravariant velocity.

Fig.2.A schematic for the setup of the immersed boundary simulation with a coordinate definition, b grid distribution and c grid nodes near the upper wall.Note that the grid for the immersed boundary simulation is designed in a way that the top and bottom walls do not coincide with grid nodes in the wall-normal direction.

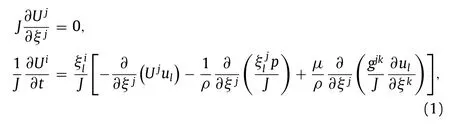
wherexiandξiare the Cartesian and curvilinear coordinates,respectively,are the transformation metrics,Jis the Jacobian of the geometric transformation,uiis thei-th component of the velocity vector in Cartesian coordinates,Ui=is the contravariant volume flux,gjk=are the components of the contravariant metric tensor,ρis the density,μis the dynamic viscosity,andpis the pressure.The governing equations are discretized in space using a second-order accurate central differencing scheme,and integrated in time using the fractional step method.An algebraic multigrid acceleration along with generalized minimal residual method (GMRES) solver is used to solve the pressure Poisson equation.A matrix-free Newton-Krylov method is used for solving the discretized momentum equation.More details about the flow solver can be found in Refs.[14-16].

In the CURVIB method,the background grid nodes are classified as solid nodes inside solid body and fluid nodes in the fluid.The fluid node with at least one neighbour of solid nodes is marked as the IB node (e.g.pointbin Fig.1a).The velocity of the IB node is reconstructed using the velocity at pointcand the velocity at the boundary to supply boundary conditions for the outer flow simulations,in which the velocity atcis interpolated from the surrounding fluid nodes.For DNS and wall-resolved large-eddy simulation,the linear interpolation is employed for the velocity reconstruction.For flows at high Reynolds number,computationally efficient wallmodeled large-eddy simulation is preferred,in which the velocity is reconstructed using a wall model [17-22].The CURVIB method employs a hybrid staggered/non-staggered grid layout,as shown in Fig.1b,for solving satisfying the divergence-free conditions.The equations are advanced in time using a second-order fractional step method.The procedure for advancing the flow field for one time step is summarized as follows:

1 Solve the momentum equation for the intermediate velocity at volume centers,with the velocity reconstructed at the IB nodes serving as boundary conditions;

2 Compute the contravariant velocity at the face centers using the velocities at volume centers;

3 Correct the contravariant velocity at face centers,which are next to IB nodes,to satisfy the global mass conservation;

4 Solve the Poisson equation with its right-hand-side term computed using the contravariant velocities;

5 Obtain the final velocity and pressure for this time step.

More details about the CURVIB method can be found in Refs.[8,9,23,24].

We carry out simulations of fully developed turbulent channel flow to evaluate the capability of the CURVIB method in predicting the near-wall turbulence.The Reynolds number based on the wall friction velocity isReτ=uτδ/ν=180,whereνis the kinematic viscosity,uτ=is the wall friction velocity,andδis the half height of the channel.The flow is driven by a mean pressure gradient in the streamwise direction to maintain a constant mass flux.

A schematic for the setup of the immersed boundary simulation is shown in Fig.2.The streamwise,wall-normal and spanwise directions are denoted byx,yandz,respectively.The size of the computational domain isLx×Ly×Lz=2πδ×2.02δ×πδ,in which the computational domain in wall-normal direction is set in the range ofy∈[−0.01,2.01] with two manually located walls aty=0 andy=2 between grid nodes.The numbers of grid nodes areNx×Ny×Nz=256×134×256.In order to fully examine the accuracy,the grid for the immersed boundary simulation is designed in a way that the top and bottom walls do not coincide with grid nodes in wall-normal direction.The wall-normal grid spacing near the upper and lower walls isΔy=0.0044δ,with the correspondingΔy+=Δyuτ/ν=0.80.The grid nodes are uniformly distributed in the streamwise and spanwise directions,respectively,with the grid spacings calculated to beΔx+=4.4 andΔz+=2.2,respectively.Periodic boundary conditions are applied in the streamwise and spanwise directions.The time step is set toΔt=0.004πδ/ub,which corresponds to a CFL (Courant–Friedrichs–Lewy) number ofubΔt/Δx=0.5,whereubis the bulk velocity.This setup for time step indicates about 500 steps for one flow through.For the body-fitted simulation,the size of the computational domain isLx×Ly×Lz=2πδ×2δ×πδwith the number of grid nodes ofNx×Ny×Nz=256×128×256.The height of the first off-wall grid node isΔy=0.004δ,with the correspondingΔy+=0.72.The time step for the body-fitted simulation is set to be the same with that of the immersed boundary simulation.Both simulations are firstly carried out until the flows are fully developed,then additional simulations are carried out to obtain turbulence statistics for about 100 flow throughs.

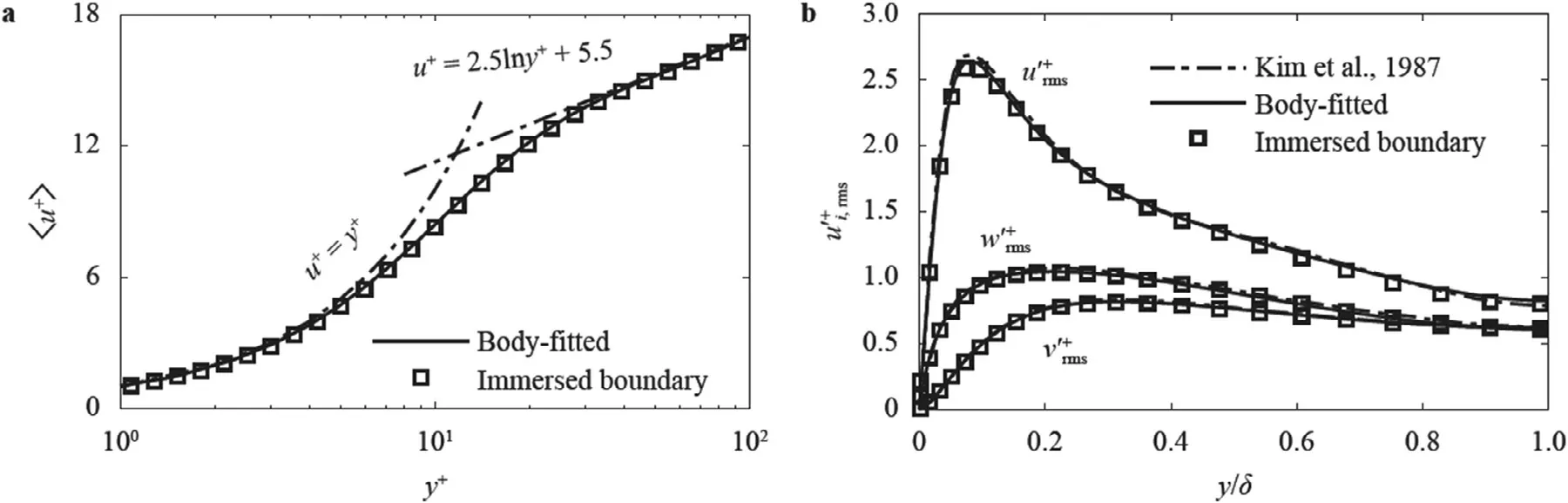
Fig.3.Comparison of a time-averaged streamwise velocity and b root-mean-square of velocity fluctuations.

Fig.4.Comparison of a total shear stress −〈u v〉/+d〈u+〉/dy+ and b Reynolds shear stresses −〈u v〉/ .

We first compare the profiles of mean streamwise velocity in Fig.3a and the root-mean-square of the velocity fluctuations in Fig.3b from the immersed boundary simulation with those from the body-fitted simulation carried out by Kim et al.[25].As seen,the immersed boundary predictions agree well with the bodyfitted results and the reference.Then,we compare the profiles of total shear stress and Reynolds shear stress in Fig.4.As discussed in Ref.[26],the following equation leads to the profile of a straight line in Fig.4a for the total shear stress:

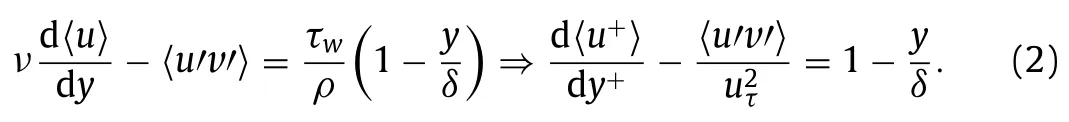
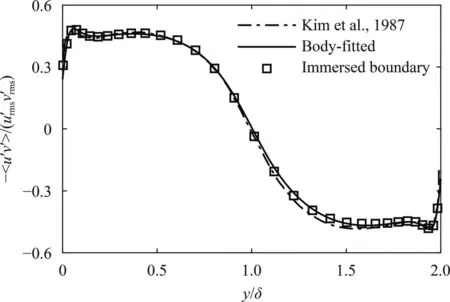
Fig.5.Correlation coefficients of u′ and v′.

Meanwhile,in the middle of the channel aty/δ=1,due to d〈u+〉/dy+=0,the Reynolds shear stress −should have a slope of −1 with respect toy/δ,as shown in Fig.4b.It is observed clearly that both total shear stress and Reynolds stress from the immersed boundary simulations agree well with body-fitted simulation and the reference.We further compare the correlation coefficients ofu′andv′in Fig.5.It can be seen that there is a relatively strong correlation betweenu′ andv′ in a wide range ofy/δnear the wall,which indicates certain coherent motions in the wall region.As discussed in Ref.[25],an observed weak peak aty+≈12 shows the location of the maximum production and the maximum streamwise velocity fluctuation.It is observed that all these features are well predicted by the immersed boundary simulations.

Fig.6.Root-mean-square of vorticity fluctuations a ωx,rms, b ωy,rms and c ωz,rms,normalized by mean shear.

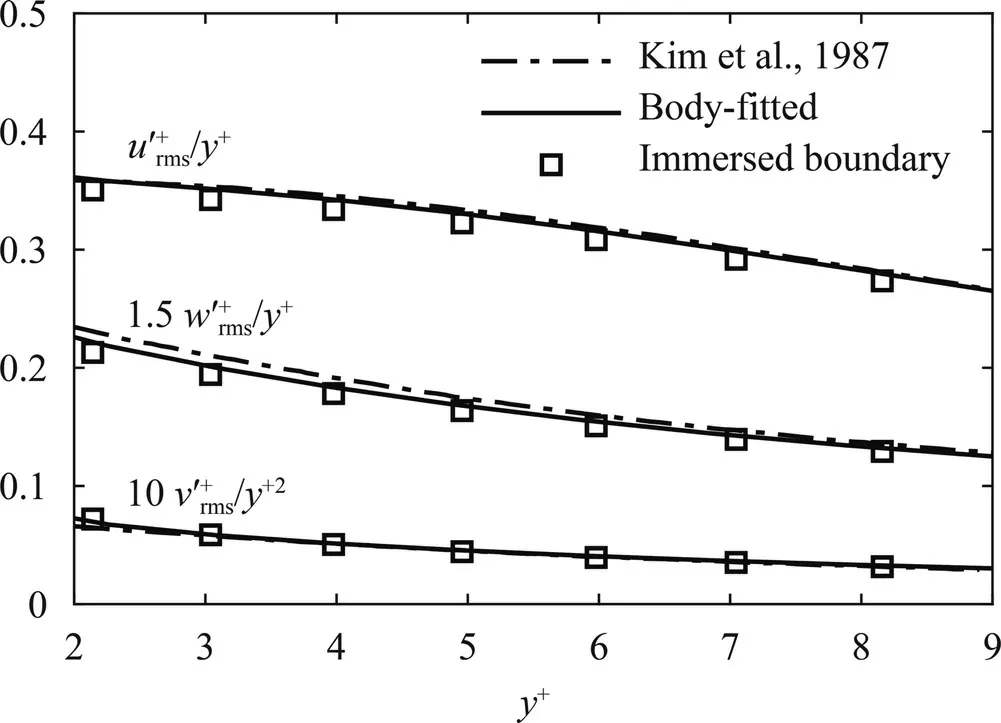
Fig.7.Comparison of the near-wall behavior of velocity fluctuations:/y+,/y+2 and /y+.

Next,we compare the profiles of rms of the vorticity fluctuations in Fig.6.It can be seen the immersed boundary simulation can accurately predict the vorticity fluctuations.As is explained in Ref.[25],the local minimum and the local maximum of the streamwise vorticity indicate the edge and centre of the vortex,respectively,leading to an estimation of the centre of the streamwise vortex located aty+=20 with radiusr+=15.

Then,we examine the near-wall scaling of velocity fluctuationsui,rmsin Fig.7 to evaluate the capability of the employed CURVIB method in predicting the near-wall behavior,where the boundary conditions are not directly applied at the wall.Applying the no-slip boundary condition and continuity equation to the Taylor series expansion of the velocity components [26],it can be obtained that the streamwiseand spanwisew+rms have a linear scaling ofy+,while the wall-normalhas a behavior ofy+2scaling,as shown in Fig.7.It is observed that the immersed boundary method can accurately predict such scalings.

At last,we focus on the capability of the immersed boundary method in predicting time-averaged pressure and statistics of pressure fluctuations.We show the profiles of time-averaged pressure and rms of pressure fluctuations in Fig.8.It is observed that the predictions of the immersed boundary simulation agree well with those from the body-fitted simulations,although somewhat differences are observed for the peak of the time-averaged pressure.In Fig.9,we compare the normalized wavenumber-frequency spectra of the pressure fluctuations at two wall-normal locations,which are compted using the following equations:

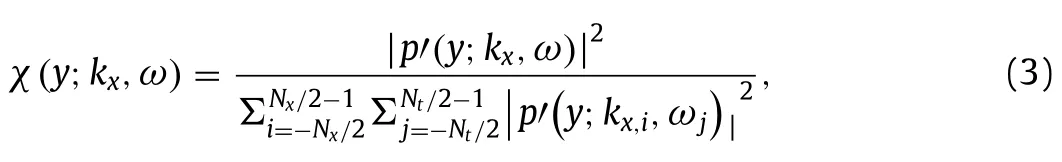
wherekxandωare the streamwise wavenumber and frequency,respectively,andp′(y;kx,ω)is the spatial-temporal discrete Fourier transform (DFT) of pressure fluctuationp′(y;x,t)=p(y;x,t)−〈p(y;x,t)〉.Ensemble averaging for|p′(y;kx,ω)|2is carried out in the spanwise direction and in time with 50% overlapping.To make comparisons between the two simulations,the body-fitted result is shown by contour floods,whereas the immersed boundary result is indicated by red solid contour lines.It is observed that the energy-containing regions of pressure fluctuations predicted by the two simulations are almost identical at the considered wall-normal locations with slight differences observed at high wavenumber and frequency for the spectra at the wall,which indicates that the immersed boundary method is able to predict the space-time structure of pressure fluctuations at the same accuracy as the body-fitted method.

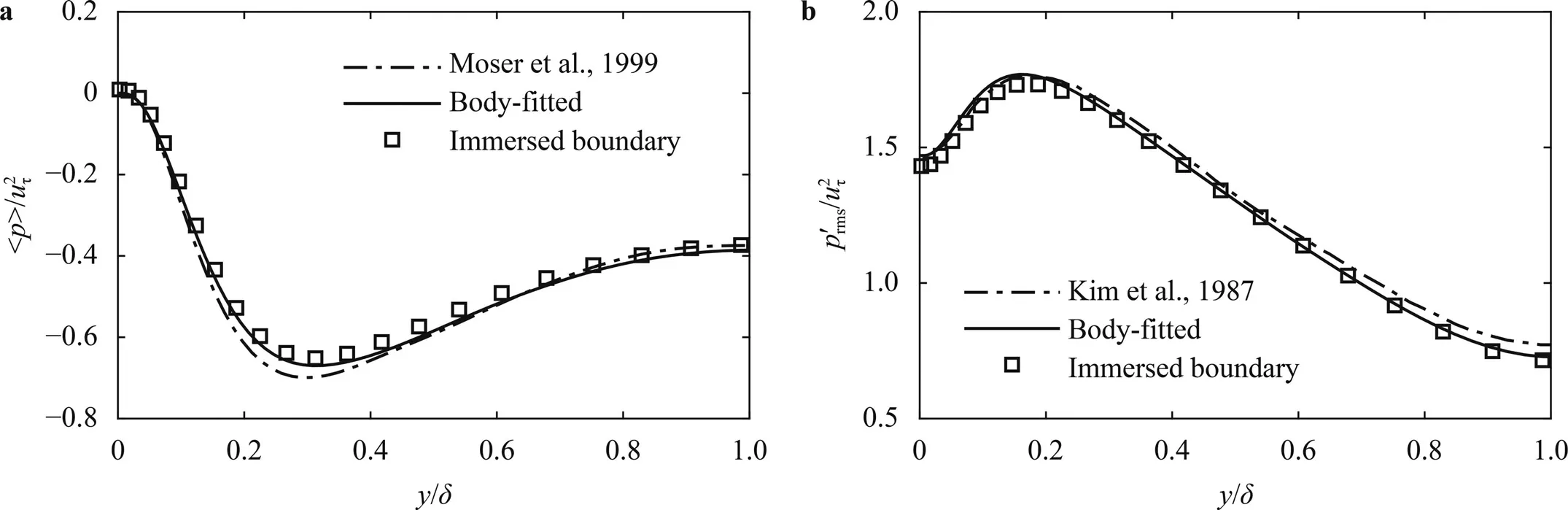
Fig.8.Comparison of a time-averaged pressure and b root-mean-square of the pressure fluctuations.

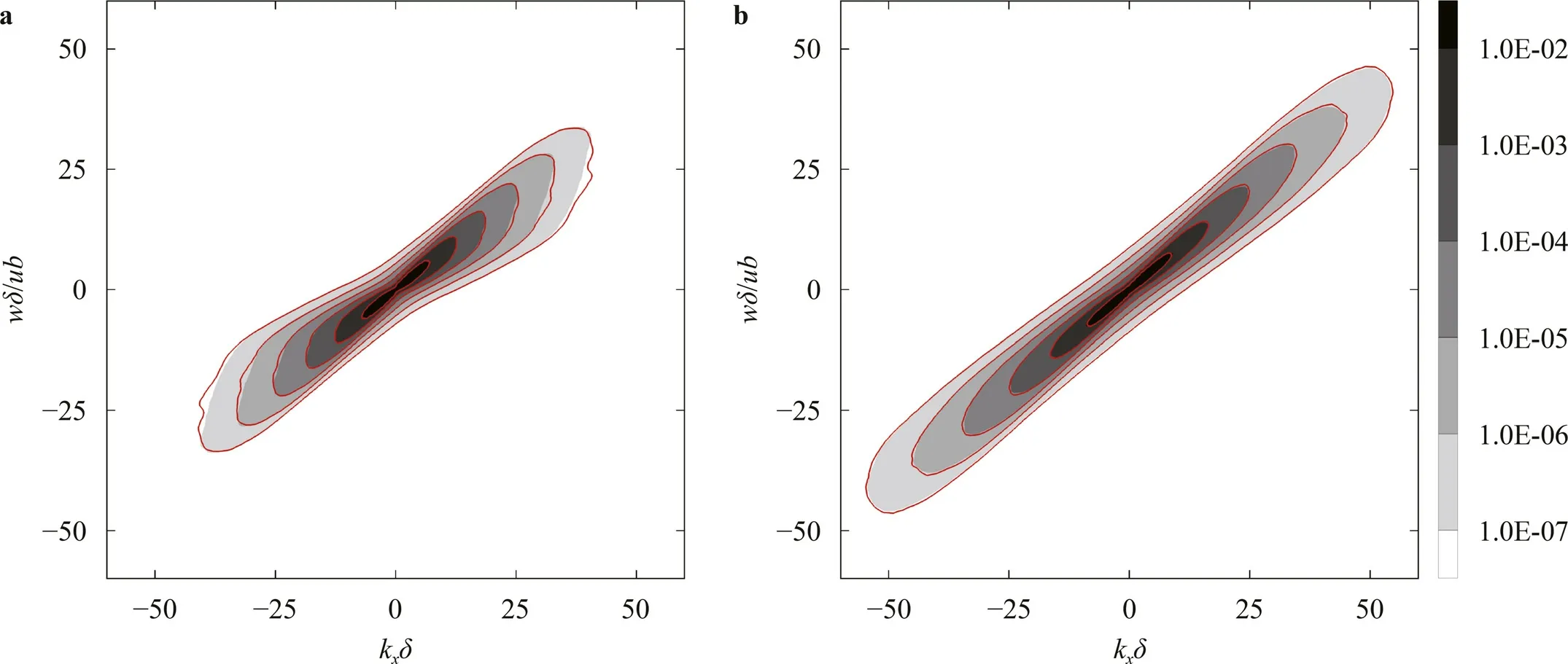
Fig.9.Normalized wavenumber-frequency spectra of pressure fluctuations at a wall and b y+=30 computed from the two simulations.To make comparisons,the bodyfitted result is shown by contour floods,whereas the immersed boundary result is indicated by red solid contour lines.

In this work,we examine the capability of the curvilinear immersed boundary method in predicting near-wall turbulence of the turbulent channel flow at Reynolds numberReτ=180 by comparing its predictions with those from the simulation of a body-fitted method.Quantities including mean and fluctuations of velocity,vorticity and pressure,shear stresss,correlation coefficient ofu′andv′,near-wall scaling of velocity fluctuations and wavenumberfrequency spectra of pressure fluctuations are compared.Two conclusions can be drawn as follows:(1) The accuracy of the curvilinear immersed boundary method in predicting statistics of velocity and pressure fluctuations is almost the same as that of the body-fitted method;(2) For the wavenumber-frequency spectra of pressure fluctuations,minor fluctuations are observed at high wavenumber and high frequency for the immersed boundary predictions,which might not be of great significance as the energy at that wave number and frequency is several orders of magnitude smaller than the maximum value.

Since the Cartesian grid is employed in this work,similar conclusions are expected for the immersed boundary method based on the Cartesian grid with similar near wall treatments.Only the case of the turbulent channel flow at a low Reynolds number is tested in this work for which DNS is feasible.Further studies need to be carried out using cases at high Reynolds numbers to test LES and the immersed boundary method with wall models.Furthermore,evaluation on the near wall accuracy of the CURVIB method will be carried out in the future work for cases with complex boundaries.

Declaration of Competing Interest

The authors declare that there are no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgment

This work was supported by the National Natural Science Foundation of China (NSFC) Basic Science Center Program for“Multiscale Problems in Nonlinear Mechanics”(No.11988102) and the Strategic Priority Research Program,Chinese Academy of Sciences(CAS) (No.XDB22040104).