Error of large-eddy simulation in the wall pressure fluctuation of a turbulent channel flow

Rong Li ,Bowen Yng ,Zixun Yng ,∗,Shizo Wng ,Guowei He

a State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China

b School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 10 0 049, China

ABSTRACT We analyze the error of large-eddy simulation (LES) in wall pressure fluctuation of a turbulent channel flow.To separate different sources of the error,we conduct both direct numerical simulations (DNS)and LES,and apply an explicit filter on DNS data to obtain filtered DNS (FDNS) data.The error of LES is consequently decomposed into two parts:The first part is the error of FDNS with respect to DNS,which quantifies the influence of the filter operation.The second part is the difference between LES and FDNS induced by the error of LES in velocity field.By comparing the root-mean-square value and the wavenumber-frequency spectrum of the wall pressure fluctuation,it is found that the inaccuracy of the velocity fluctuations is the dominant source that induces the error of LES in the wall pressure fluctuation.The present study provides a basis on future LES studies of the wall pressure fluctuation.

Keywords:Wall pressure Large-eddy simulation Turbulent channel flow

An accurate prediction of wall pressure fluctuations is a basis for the investigation of noise generation and flow-induced vibration in many engineering applications [1,2].In literature,there are extensive experimental and theoretical studies of the wall pressure,and comprehensive reviews are given by Willmarth [3] and Eckelmann [4] .

During the last two decades,numerical simulation becomes increasingly important in turbulence research.Among various simulation strategies,the direct numerical simulation (DNS) provides an accurate prediction of the wall pressure fluctuations [5–8] .However,the computational cost of DNS increases at a rate of the cube of the Reynolds number [9],and therefore,the application of DNS is limited to flows at low and moderate Reynolds numbers.The large eddy simulation (LES) uses grid to resolve large-scale motions of turbulence with the influences of the unresolved motions represented by a subgrid-scale model.LES is less expensive than DNS,and is therefore expected to become a useful tool for engineering applications.Viazzo et al.[10] used LES to study the statistics and spectra of the wall pressure fluctuations in turbulent channel flow atReτ=640 .Park and Moin [11] reported the space-time characteristics of the wall pressure fluctuations using wall-modeled LES of a turbulent channel flow atReτ=20 0 0 .They noted that the resolution required for an accurate prediction of the wall pressure fluctuations was more stringent than that of the velocity field.In the above LES studies of the wall pressure fluctuations,although some features of the wall pressure fluctuations are captured qualitatively,the error is non-negligible.

In an incompressible turbulent channel flow,the pressure is governed by the following Poisson equation and boundary conditions

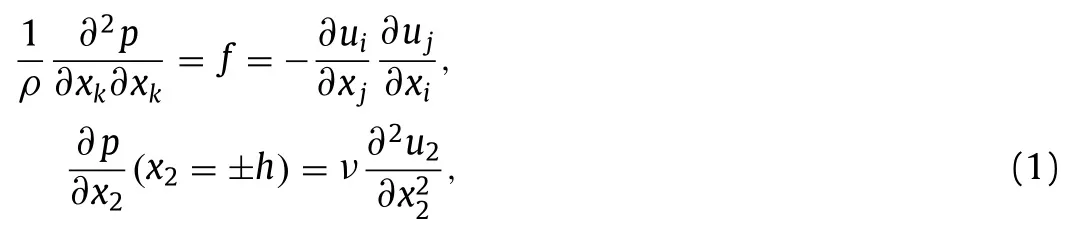
wherepdenotes the pressure,uiis the velocity,with the subscripti=1,2,and 3 being the streamwise,wall-normal,and spanwise directions,respectively,ρandνrepresent the density and kinematic viscosity,respectively,x2=±hrepresents the locations of two solid walls,andhis one-half the channel height.Filtering Eq.(1) results in the governing equation of the resolved pressure as

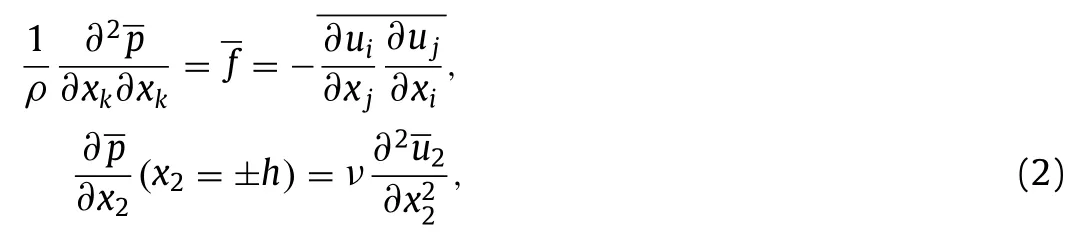
where the overline denotes a filtering operation.In LES,only the resolved part ofuiis available,and as such the pressure can be only calculated approximately by solving the following equation

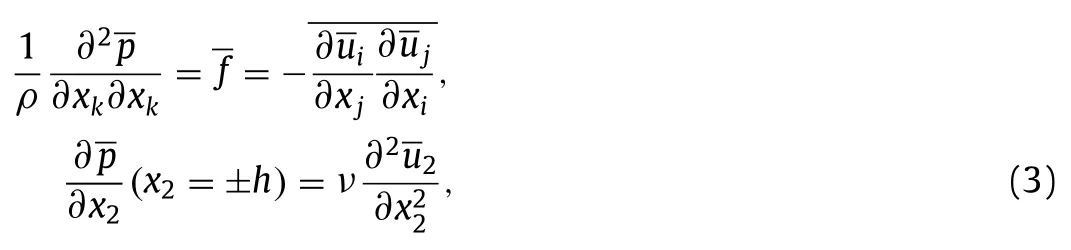
where the velocity in the source term of Eq.(2) is replaced by the resolved velocityBy contrasting Eqs.(2) and (3),it is understood that the error of LES in the pressure (with respect to the DNS result) indeed consists of two parts.The first part is induced by the filter,or equivalently,by the difference betweenuiandThe second part is caused by the inaccuracy of LES in the resolved velocity,or equivalently,by the difference between DNS and LES in.

In the present study,we aim to find the dominate source of the error of LES in the wall pressure fluctuations.For this purpose,we conduct both DNS and LES of a turbulent channel flow,and filter the DNS data to obtain filtered DNS (FDNS) data.The error induced by the filter is estimated by comparing the solutions of Eqs.(2) and(3),in whichuiandare given by DNS and FDNS,respectively.The error caused by the inaccuracy of LES inis quantified by comparing the solutions of Eq.(3) between FDNS and LES.

To collect data needed for the analyses of the error of LES in the wall pressure fluctuation,both DNS and LES of turbulent channel flows are conducted.The Reynolds number is set toReb=ubh/ν=10150,whereubis the bulk mean velocity.The corresponding Reynolds number based on the wall friction velocityuτisReτ=uτ h/ν=550.The flow is driven by a streamwise pressure gradient,which is adjusted to sustain a constant value of the bulk mean velocityub.Periodic boundary conditions are adopted in the streamwise and spanwise directions,while no-slip and nopenetration conditions are prescribed at two solid walls.The computational domain is set toL1×L2×L3=4πh×2h×2πh.For spatial discretization,all flow quantities are expanded into Fourier series in the streamwise and spanwise directions,and into Chebychev polynomials in the wall-normal direction.A third-order timesplitting method [12] is utilized for time advancement.Table 1 summarizes the number of grid pointsNiand grid resolutionΔxiof DNS and LES.The dynamic Smagorinsky model [13,14] is chosen to conduct LES.

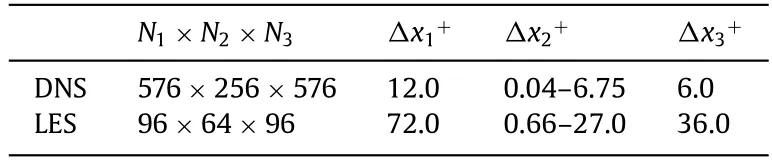
Table 1 Number of grid points Ni and grid resolution Δxi for DNS and LES of turbulent channel flow at Re τ=550.

To obtain the FDNS flow field,a sharp cut-off filter in the spectral space is applied.Below are the descriptions of the filter.The velocity fielduiof DNS is first expanded into coefficients of Fourier series and Chebyshev polynomials as

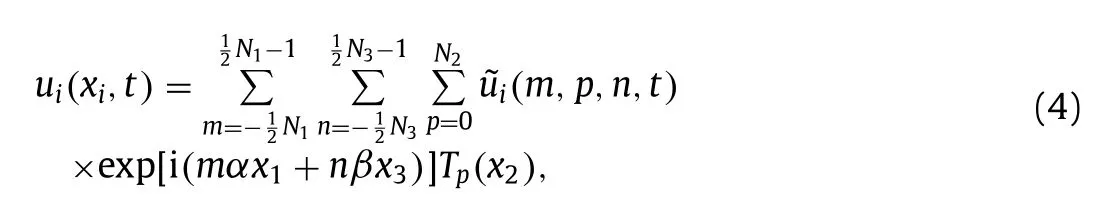
whereα=2π/L1 andβ=2π/L3 are the wavenumber resolutions in the streamwise and spanwise directions,respectively,Tp(x2)is thepth-order Chebyshev polynomial,and the tilde denotes the spectral coefficients of an arbitrary flow quantity.The spectral coefficients of velocityare then truncated to obtain the FDNS velocity,viz.

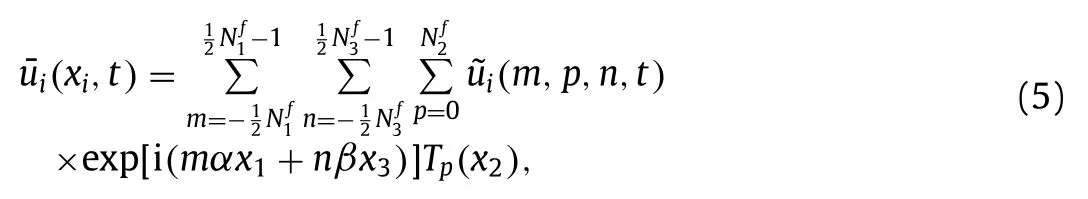
In the applications of the flow-induced vibration and noise,the wavenumber–frequency spectrum of wall pressure plays an important role.Therefore,we also examine the error of LES in the wavenumber–frequency spectrum of the wall pressure fluctuation,which is calculated using the method of Choi and Moin [6].Specifically,a time series of the wall pressure fluctuationp(x1,x3,t)is divided into intervals with 50% overlapping with the neighboring ones.Each time interval containsNs=512 time samples.The time length between two samples is=0.298,which gives the highest frequency of=10.54.In this paper,the superscript "+" is used to denote variables non-dimensionalized using the viscous lengthscaleν/uτand wall-friction velocityuτas characteristic length and velocity scales,respectively.Consequently,the time duration of each time interval iswhich corresponds to a frequency resolution ofΔω+==4.1×10−2.

The wall pressurepin each interval is Fourier transformed inx1andx3-directions and in time to obtain its Fourier coefficientsas

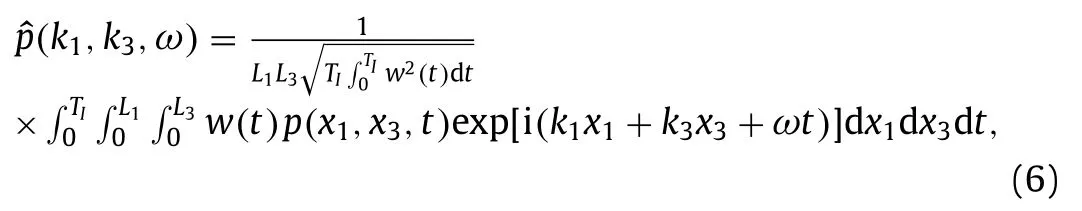
wherek1andk3are wavenumbers in thestreamwise and spanwise directions,respectively,andw(t)is astandardHanning window function.The wavenumber–frequency spectrum of the wall pres-

sure fluctuationΦpp(k1,k3,ω)is then calculated as Eq.(7)

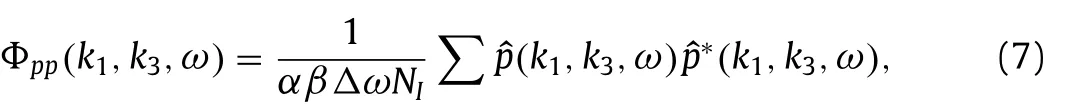
where the asterisk“∗”denotes complex conjugate.The summation is performed over all time intervals,andNIis the total number of time intervals.Taking the summation ofΦpp(k1,k3,ω)overk3 yields thek1−ωspectrum of the wall pressure fluctuationΦpp(k1,ω),viz.

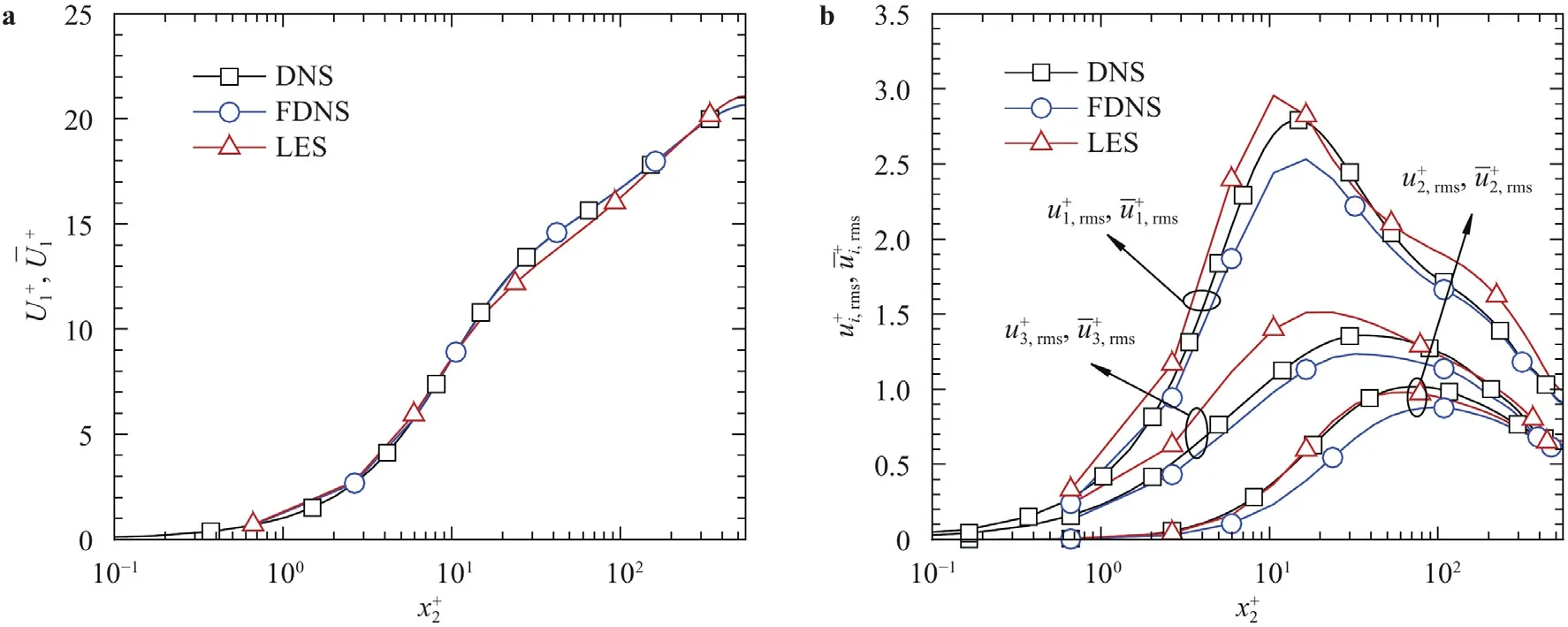
Fig.1.Profiles of a mean streamwise velocity and b RMS velocity obtained from DNS,FDNS,and LES.

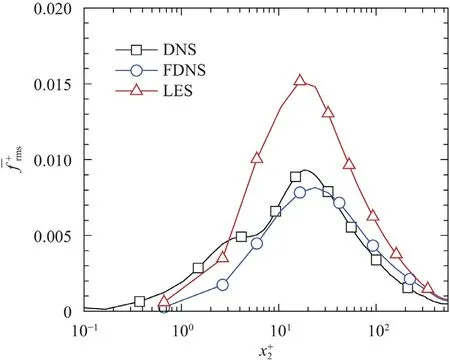
Fig.2.Profiles of the RMS values of the pressure source term obtained from DNS,FDNS,and LES.

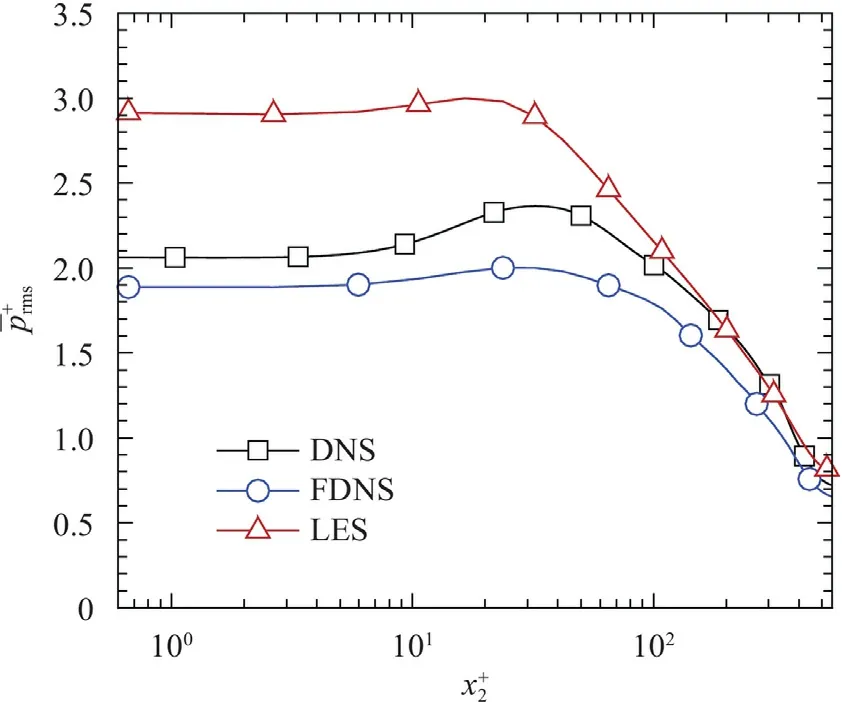
Fig.3.Profiles of the resolved RMS pressure obtained from DNS,FDNS,and LES.

Figure 4 compares thek1−ωspectrum of the wall pressure fluctuationobtained from DNS,FDNS,and LES.To facilitate a quantitative comparison of the results,profiles ofas a function ofω+at specific streamwise wavenumbers,i.e.,=0.005,0.018,0.036,are depicted in Fig.5.From Figs.4a and 5,it is observed that the FDNS and DNS results are in general consistent near the convective peak,which is located at relatively low streamwise wavenumber=0.005 and frequencyω+=0.1.In the low-value region at larger streamwise wavenumbers or frequencies,the FDNS slightly under-predicts the ’energy’level of the spectrum of the wall pressure fluctuation.In this regard,the filtering only influences the resolved pressure fluctuation near the cut-off wavenumbers and high frequencies,while the small wavenumbers and low frequencies corresponding to largescale and long-term motions remain almost unchanged.Figures 4b and 5 show that the disagreement between LES and DNS is apparent near the convective peak.The LES overestimates the spectral magnitude of the wall pressure fluctuation.

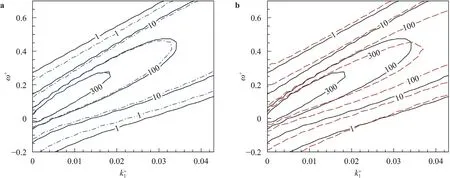
Fig.4.Isopleths of the k1 −ω spectrum of the wall pressure fluctuation obtained from a DNS and FDNS and b DNS and LES.The solid,dash-dotted and dashed lines represent the results of DNS,FDNS and LES,respectively.

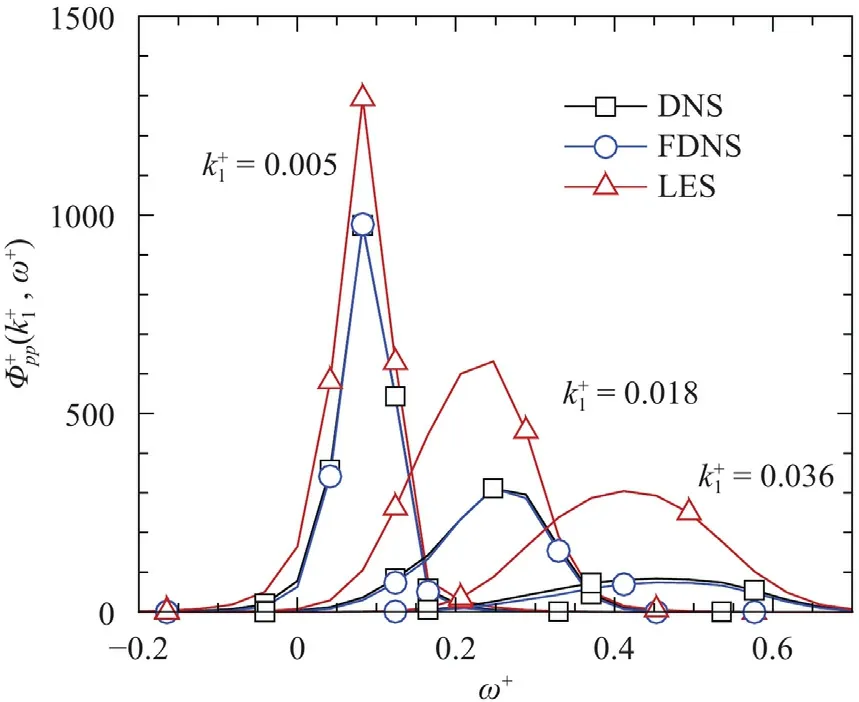
Fig.5.Profiles of the k1 −ω spectrum of the wall pressure fluctuationat specific streamwise wavenumbers.

The wavenumber-dependent convective velocityUc(k1)and spectral bandwidthB(k1)are two key indicators of the wavenumber–frequency spectrum,which are defined respectively as [15]:

and

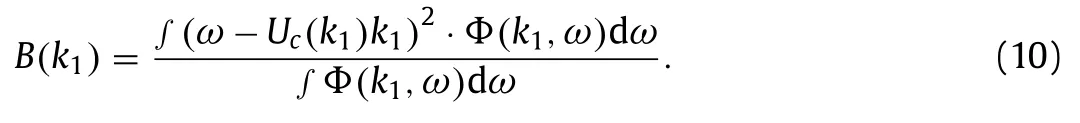
Figure 6 compares the values ofUc(k1)andB(k1)of thek1 −ωspectrum of the wall pressure fluctuation obtained from DNS,FDNS,and LES.In consistent with the observations from Figs.4a and 5,the results of FDNS are in good agreement with those of DNS.From Fig.6a,it is seen that the convective velocityUc(k1)obtained from LES is lower than the DNS and FDNS results,while Fig.6b shows that the LES under-estimates the spectral bandwidthB(k1)at high wavenumbers.In the present study,to analyze the error of LES in the wall pressure fluctuation,DNS and LES of a turbulent channel flow atReτ=550 are conducted,and FDNS data are obtained by applying a spectral cut-off filter on the DNS data.The RMS pressure and wavenumber–frequency spectrum of the wall pressure fluctuation of FDNS are in general consistent with the DNS results.The filtering operation only influences the resolved pressure near the cut-off scale.In contrast,the LES overestimates both the RMS value and the spectral energy level of the wall pressure fluctuation,indicating that the error in the velocity gradient is the dominant source that induces the error in the wall pressure fluctuation.The results obtained from the present study suggest that improving the accuracy of the velocity gradient is crucial for making better predictions of the wall pressure fluctuation in LES.As a final remark of this paper,we note that the present study focuses on identifying the issue of LES that the error in the wall pressure fluctuation is highly dependent on the error in the velocity fluctuations.This conclusion is drawn based on the test of turbulent channel flow atReτ=550 using specific grid resolution and numerical scheme.In the future,the influences of Reynolds number,grid resolution,and numerical scheme need to be examined systematically to provide a more comprehensive understanding of the problem.

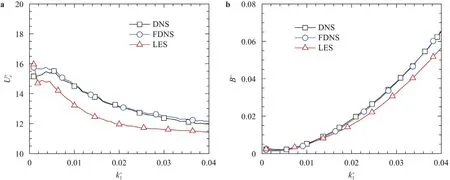
Fig.6.Wavenumber-dependent a convective velocity and b spectral bandwidth of the k1 −ω spectrum of the wall pressure fluctuation.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This research is supported by the National Natural Science Foundation of China (NFSC) Basic Science Center Program for“Multiscale Problems in Nonlinear Mechanics”(Grant 11988102) and the National Key Project (Grant GJXM92579).Shizhao Wang acknowledges the support from the National Natural Science Foundation of China (Grant 11922214).