培养初中生数学思维灵活性的教学策略

肖文记

摘  要：思维的灵活性是指思维活动过程中智力的灵活程度。发展思维灵活性可以从以下三个方面着手：一是起点灵活，从不同角度出发，用不同方法解决问题;二是过程灵活，随着条件的变化而变化，有的放矢地转化问题;三是结果灵活，从不同侧面、不同层次解释事物的现象和规律。

关键词：初中数学;思维灵活性;起点灵活;过程灵活;结果灵活

初中数学知识具有内在的一致性和广泛的联系性。在教学过程中，教师要引导学生对思维材料进行广泛的联想，建立数学对象之间的关联，为思维的灵活性奠定坚实的基础。

一、在思维起点处培养思维的灵活性

要解决这个问题，教师指导学生可以从以下六个方面中的某一点出发。

（1）从条件出发，由[-3.2=-4]想到还会有哪些数取整后的结果为-4，可以借助数轴思考。

（2）将[x=-3.2]代入多项式[2x-3x，] 值是多少？

（3）令[x=-3]，可求出方程的解吗？

（4）从问题出发，要解这个方程，只需弄清x与[x]有什么关系。

（5）移项，将x用[x]的式子表示，用特殊值尝试。

（6）移项，将[x]用x的式子表示，用特殊值尝试。

思维的灵活性在于起点处的关联。从条件入手，化静为动，由一个数联想到一串数，借助数轴可以确定[x，] [x+1]与x之间的大小关系，还可以确定[x]与x之间的结构关系;从问题入手，方程可以变为代数式，化未知为已知，理清两个变量之间的关联，从特殊到一般，正反互助，在起点处呈现思维的灵活性。

二、在思维过程中培养思维的灵活性

学生解题缺少过程的优化，教师可以因势利导，引发深度思维。例如，在教学教材七年级上册“整式的加减”时，教师出示题目：某班决定购买5副羽毛球拍和30只羽毛球，已知一副羽毛球拍的价格是30元，一只羽毛球的价格是2元。甲、乙两商店举行促销活动，甲商店给出的优惠是：所有商品打八折;乙商店给出的优惠是：买一副羽毛球拍送4只羽毛球，问如何购买花钱少，最少费用是多少。

小组1：在甲商店购买全部商品的费用：[0.8×][5×30+2×30=168（元）;] 在乙商店购买全部商品的费用：[5×30+2×30-5×4=170（元）;] 若在两店混合购买有5种情况（略），[167.6>167.2>166.8>][166.4>166]，所以在乙店购买5副球拍，在甲店购买10只羽毛球花費少，最少费用为166元。

师：小组1解答分类太多，而且没有包含所有情况，谁还有不同的做法？

小组2：设在乙商店购买a副球拍，在甲商店购买[5-a]副球拍和余下的羽毛球，总费用为[5-a×][30+30-4a×2×0.8+30×a=168-0.4a。] 当a = 5时，费用最少，为166元。

师：为什么混合购买花费最小呢？

小组3：购买1副球拍和4只羽毛球，在乙商店需要付30元，在甲商店需要付30.4元。将1副球拍和4只羽毛球打包为一个整体购买，在乙商店花费小。购买5副羽毛球拍和30只羽毛球分为两部分，一部分是1副球拍和4只羽毛球的5倍在乙商店花费小;另一部分是余下的10只羽毛球在甲商店购买，一共费用为166元。

思维的灵活性在于过程中的优化，从数到式，感受到字母表示数的便捷，从算式到整式，探究一般化的算法，从整体思维的角度理清了混合购买花费小的实质。教学策略由浅及深，由具体到抽象，构建不同算法;从现象到本质，在不断优化的过程中展现思维的灵活性。

三、在结果运用中培养思维的灵活性

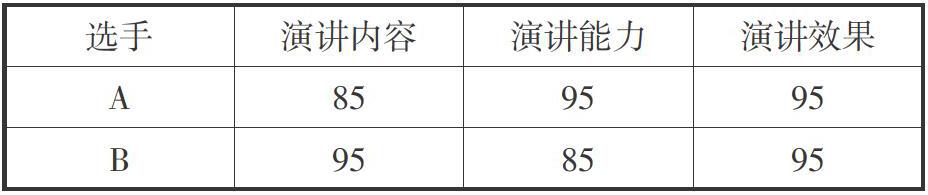
学生的探究往往忽略结果的聚合，教师可以对结果进行类比迁移，实现聚合思维。例如，在教学教材八年级下册“加权平均数”时，教师出示题目：一场演讲比赛，评委要从演讲内容、演讲能力、演讲效果三个方面打分，然后根据三项成绩计算选手的综合成绩，预选赛中前两名选手的单项成绩如下表所示。

（1）如果你是评委，你如何确定他们的综合成绩？

（2）根据综合成绩，你能确定哪位选手代表学校参加区级比赛？

小组1：我们认为演讲能力最重要，确定内容、能力、效果三个项目的成绩按照3∶4∶3分配，计算得出A选手的成绩为85 × 0.3 + 95 × 0.4 + 95 × 0.3 = 92，B选手的成绩为95 × 0.3 + 85 × 0.4 + 95 × 0.3 = 91，所以选A选手。

小组2：我们认为演讲内容最重要，确定内容、能力、效果三个项目的成绩按照4∶3∶3分配，计算得出A选手的成绩为85 × 0.4 + 95 × 0.3 + 95 × 0.3 = 91，B选手的成绩为95 × 0.4 + 85 × 0.3 + 95 × 0.3 = 92，所以选B选手。

师：不同的权重产生不同的结果。还有不同的意见吗？

小组3：我认为可以分两步处理。我们组每个人处理数据的权重各不相同，我确定内容、能力、效果三个项目的成绩按照4∶3∶3分配，小明按照2∶5∶3分配，小天按照2∶3∶5分配，计算出各自的成绩，然后给我、小明、小天三人的结果赋予不同的权重2 ∶1∶1，再分别计算两位选手的成绩。

思维的灵活性在于对结果的类比和聚合，小组1赋权计算，小组2类比小组1微调权重，两种算法让学生感受到同一组数据在不同权重下算出不同结果，运用结果做出了不同的选择。小组3学生汇集前两组的算法，把权重运用到了极致，先分类再分步，展现了思维的类比、转化与聚合，在对结果的整合、归纳中展现思维的灵活性。

四、结束语

从以上案例可以看出，思维灵活性的实质是类比迁移，由点到线，由孤立到关联，由单一到多样，由静止到动态，由具体到抽象，经历归纳与概括，实现思维的灵活迁移。

参考文献：

[1]中华人民共和国教育部制定. 义务教育数学课程标准（2011年版）[M]. 北京：北京师范大学出版社，2012.

[2]曹才翰，章建跃. 中学数学教学概论（第二版）[M]. 北京：北京师范大学出版社，2008.

[3]杜维林. 数学教学中培养学生思维灵活性的两种策略[J]. 中学数学，2017（24）.