Sc掺杂SnO2稀磁半导体的第一性原理研究

李 聪, 姜宏伟, 郑友进, 郝国栋

(牡丹江师范学院 物理系 黑龙江省新型碳基功能与超硬材料重点实验室， 牡丹江 157011)

1 引 言

SnO2是一种典型的半导体，具有理想的禁带宽度(3.6 eV[1])和可观的激子结合能(130 meV[2])，因此在太阳能电池、激光器件、涂层材料等众多领域展现出了良好的应用潜质[3, 4]. 为了进一步提高SnO2的物理化学性质，许多研究人员采用离子掺杂的手段对SnO2的电子结构进行调控. 相关的实验和理论研究表明：In掺杂能使SnO2实现p导电，空穴浓度随In掺杂量增加而增加[5]；Sb掺杂SnO2能通过施主-受主能级跃迁实现紫外光激发[6]；Fe掺杂能有效降低SnO2的禁带宽度，进而增加SnO2对可见光的吸收系数，提高其光电效率[7]；Cr掺杂能拓展SnO2的吸收谱宽度并增加SnO2在可见光区的反射率和折射率[8]. 更为重要的是，有学者发现Fe、Co、Mn等元素掺杂能使SnO2具有铁磁性[7,9,10]，这使得SnO2成为一种潜在的稀磁半导体. 除此之外，Salmani等[11]的理论研究表明V、Cr掺杂能够引入自旋极化电子态从而使SnO2具有室温铁磁性. 唐小梅[12]则通过实验研究证实K掺杂的SnO2样品呈室温铁磁性，饱和磁化强度随掺杂浓度升高而增强. 然而，理想稀磁半导体的磁性来源应该是本征的，即贡献磁矩的自旋电子是被诱导极化的而不是由掺杂直接引入. Fe、Co、Mn等元素的氧化物大都具有磁性，因而这些元素掺杂的半导体的磁性很可能来源于体系中形成的金属氧化物(第二相). 为了避免这种磁性来源的混淆，采用非磁元素作为掺杂剂成为一种行之有效的方法[13, 14]. 这其中，稀土元素Sc具有与镧系稀土相似的活跃电子态，又不像镧系元素那样具有较大的离子半径导致掺杂困难，因而受到了广泛关注[15, 16]. 尤其在文献[16]的研究中证实了Sc掺杂能有效诱导Zn空位形成，进而产生自旋极化的O-2p态电子使ZnO具有铁磁性，表明Sc是一种能够诱发半导体本征铁磁性的非磁掺杂剂. 然而，Sc掺杂SnO2磁学性质的相关研究却鲜见报道. 基于以上分析，本文采用第一性原理方法系统研究了Sc掺杂SnO2的电子结构和磁学性质，研究结论对SnO2稀磁半导体的进一步开发具有重要的理论指导意义.

2 计算模型与方法

SnO2具有金红石结构，属于P4/mnm空间群. 在本文计算中，每个原胞含有两个SnO2分子，结构为Sn2O4. 计算选用的基础模型为2×2×2 SnO2超胞，结构为Sn16O32(如图1). 在基础模型中选取1或2个Sn点位替换为Sc，建立Sc1Sn15O32和Sc2Sn14O32结构. 双掺Sc时，使两个Sc原子的相对距离最远以避免团簇效应. 考虑到与Sc掺杂ZnO的情形不同，掺杂SnO2时Sc是受主杂质，因此从电价平衡角度分析，Sc掺杂易使SnO2晶格产生O空位. 为了进一步讨论Sc掺杂和O空位对SnO2磁性的影响，本文在上述模型基础上建立了含有1个O空位的Sc1Sn15O31和Sc2Sn14O31结构，通过总能量测试发现O空位出现在Sc原子近邻时体系最稳定，这是由于掺杂原子附近晶格的畸变程度最高，更容易形成空位，这与我们先前的相关研究结论相符[17].

图1 2×2×2 SnO2超胞Fig. 1 2×2×2 SnO2 supercell

本文的计算工作由Materials Studio 8.0中的CASTEP模块完成. 采用广义梯度近似中的模守恒赝势描述离子与其价电子的相互作用. 计算收敛精度为2.5×10-6eV/atom，倒格空间中的K点网格为3×3×4，单原子应力参数为0.5 eV/nm. 计算中Sc、Sn、O原子的电子态配置为：Sc-3d14s2、Sn-5s25p2、O-2s22p4. 设置SnO2单胞晶格常数为实验测量值[18]：a=b=0.4737 nm，c=0.3186 nm，α=β=γ=90°. 对各个模型进行几何结构优化，而后在电子自旋极化的条件下对优化后的超晶格进行能量计算.

3 结果与讨论

3.1 结构稳定性分析

首先通过计算形成能分析了各个改性SnO2体系的稳定性，计算公式如下[19]：

Ef=EScxSn16-xO32-y-ESn16O32-xμSc+xμSn+yμO

(1)

式中EScxSn16-xO32-y表示含有Sc原子和氧空位的SnO2体系的基态能量(x=1或2，y=0或1)；ESn16O32表示纯SnO2超胞的基态能量；μSc、μSn和μO分别表示相应原子的化学势. 从计算结果(表1)可以看出，随着Sc掺杂量增加，形成能随之上升. O空位的出现并未使形成能明显升高，这是由于Sc3+离子半径(0.081 nm)大于Sn4+离子半径(0.071 nm)，Sc掺杂使SnO2晶格出现局部的压缩畸变，导致该区域的原子受到应力作用而偏离原有位置. 在此我们还计算了各个Sc掺杂SnO2体系的原子间结合能，公式如下[20]：

(2)

式中Etot为各体系的基态总能量，n、m、l分别为体系中Sc、Sn、O原子个数. 从计算结果(如表1所示)可知，Sc掺杂后与未掺杂时相比SnO2晶格中原子间的结合作用减弱，且Sc掺杂量越大，结合能越大，原子间结合作用越弱. 而Sc掺杂量越大，晶格畸变程度越高，体系中各原子所受的应力作用越强，进一步使得Sn-O键稳定性降低而容易断裂，因此Sc掺杂易使SnO2晶格中形成空位缺陷. 结合电荷补偿机制的影响可知，在特定的Sc与O空位比例条件下，对于Sc受主掺杂来说具有电离施主属性的O空位更易形成，也因此Sc2Sn14O31结构的形成能略小于和Sc2Sn14O32结构，表明O空位能在一定程度上使Sc掺杂SnO2的稳定性提高. 在富O/富Sn条件下，O/Sn原子的化学势增加(取其单质状态下原子的平均化学势). 因此，在富O条件下Sc掺杂SnO2的形成能下降，但O空位形成能显著升高；在富Sn条件下则有利于O空位的形成.

表1 各个改性SnO2体系的形成能与净磁矩

3.2 电子结构与磁性机制

如图2所示，从计算得到的各个SnO2体系的(自旋)电子态密度可知，纯SnO2的能带主要由Sn-5p态与O-2p态杂化构成，其中Sn-5p态在导带占据主导并决定导带底位置，O-2p态则主要构成价带并决定价带顶的位置(如图2a). 由于Sn和O的s态密度很小，因此未在图中给出.

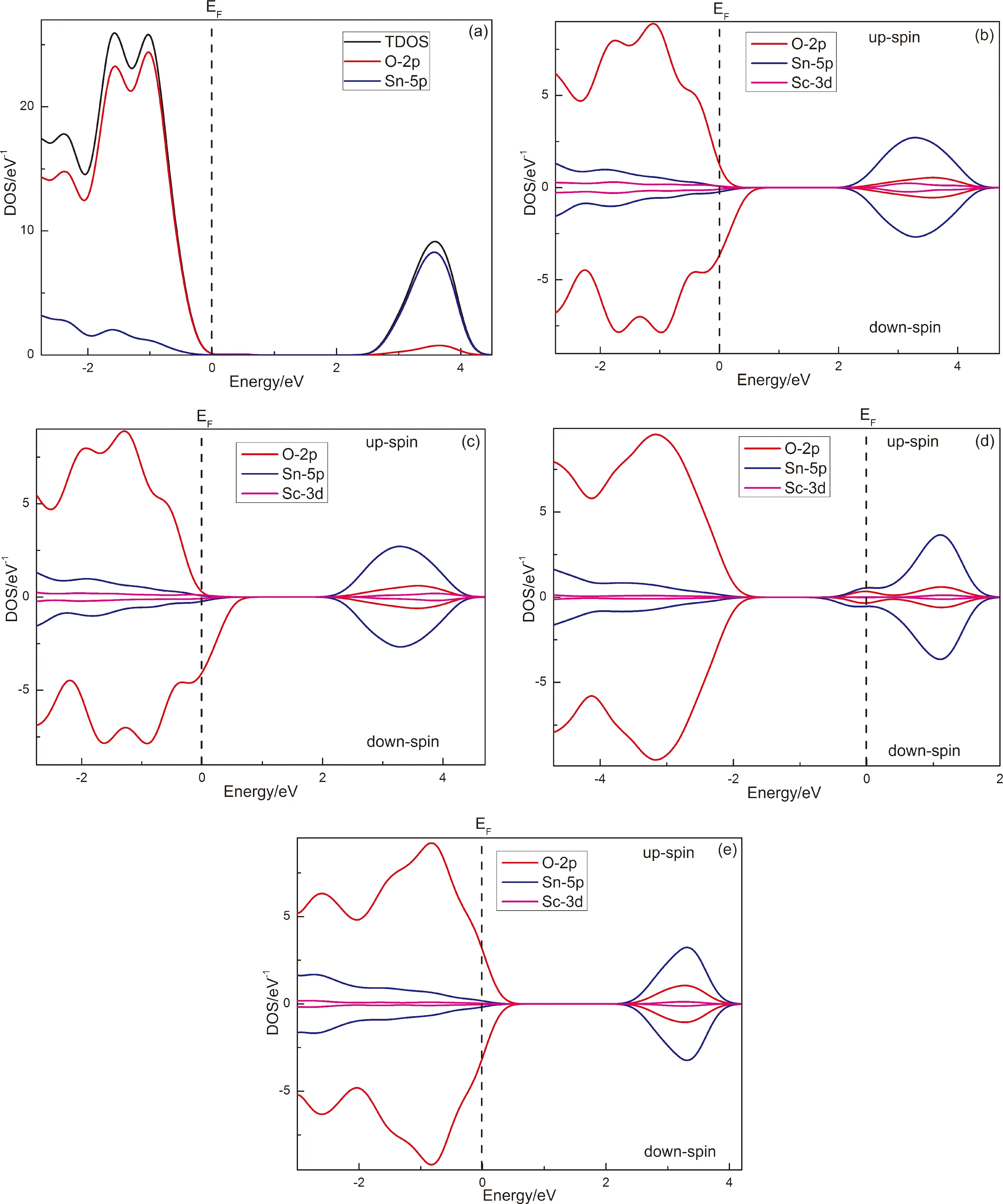
图2 各个改性SnO2体系的电子态密度：(a) Sn16O32；(b) Sc1Sn15O32；(c) Sc2Sn14O32；(d) Sc1Sn15O31；(e) Sc2Sn14O31Fig. 2 Densities of states of various modified SnO2: (a) Sn16O32; (b) Sc1Sn15O32; (c) Sc2Sn14O32; (d) Sc1Sn15O31; (e) Sc2Sn14O31

由图2b、2c可以看出，Sc原子替换Sn掺入后分别在导带和价带区域引入Sc-3d电子态，它与Sn-5p态和O-2p态重新杂化后构成新的导带底和价带顶. 更为重要的是，Sc掺杂后SnO2晶格中O-2p态的上/下自旋态密度在费米能级(EF)附近不再对称分布，表明存在自旋极化的O-2p电子为体系贡献净磁矩. 从电子迁移角度分析可知，Sc3+作为受主杂质替换Sn4+使得晶格中的一个O-2p电子未能配对而成为弱束缚电子，在O-2p轨道上不再存在另一和其自旋相反的电子，结合量子力学理论及文献[15]的报道可知，这个O-2p弱束缚电子的自旋极化为体系贡献1μB自旋磁矩(如表1所示). 从Sc1Sn15O32结构的自旋电子密度分布(如图3a)可以看出，自旋电子集中在Sc原子近邻的O原子周围，表明该O原子上存在弱束缚的2p态自旋极化电子，为体系贡献净磁矩. 掺杂的Sc原子增加，相应的未配对O-2p态电子个数增加，费米能级附近的O-2p态密度自旋不对称更明显. 根据洪德定则可知，p态未配对电子个数小于等于3时，这些电子都具有相同的自旋方向，因此净磁矩随掺杂Sc原子数量线性增加.

当1个Sc原子和1个O空位共存于SnO2晶格时，O空位类似于电离施主使得体系中出现两个未配对的Sn-5p态电子，其中一个补偿了Sc3+替换Sn4+引起的电荷缺失，另一个则自旋极化而使体系具有铁磁性. 从图2d可以看出，费米能级附近的上/下自旋态密度出现了非对称分布，与单纯Sc掺杂SnO2体系不同的是，O空位作为电离施主使得SnO2出现了n型化趋势，且此时非对称分布的态密度属于Sn-5p态. 结合Sc1Sn15O31结构的自旋电子密度分布(如图3b)可知，此时自旋电子存在于O空位近邻的Sn原子上，1μB净磁矩由一个未配对Sn-5p态电子的自旋极化贡献. 当SnO2体系中存在两个Sc原子和一个O空位时，O空位诱导的两个弱束缚Sn-5p态电子恰好补偿了两个Sc原子掺杂引起的电荷缺失，电价重新平衡，因此没有电子自旋极化，SnO2晶格发生磁性猝灭. 综合以上讨论可知，Sc掺杂SnO2体系中存在两种本征磁性来源，一是Sc掺杂诱导的未配对O-2p态电子的自旋极化，二是O空位诱导的未配对Sn-5p态电子的自旋极化，但这两种自旋极化电子分别来源于电离施主和受主，因此二者之间存在补偿效应，共存时可能引起磁性猝灭. 在实验研究中，O空位缺陷往往不易掌控，因此可通过调整Sc掺杂量以及在富氧条件下制备Sc掺杂SnO2稀磁半导体的方式减少O空位形成，从而避免磁性猝灭的发生.

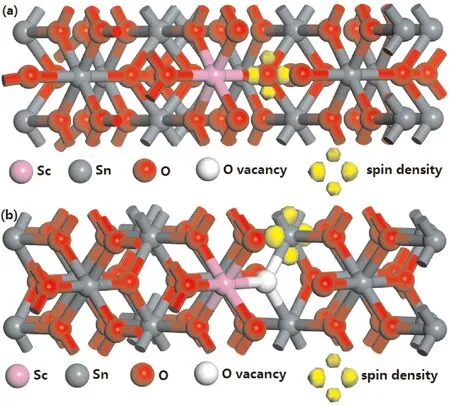
图3 自旋电子密度分布(沿[001]晶向截取的部分原子层)：(a) Sc1Sn15O32；(b) Sc1Sn15O31Fig. 3 Spin electron densities (part of the atomic layers taken along the [001] crystal direction): (a) Sc1Sn15O32; (b) Sc1Sn15O31

3.3 居里温度

能否实现室温铁磁性是稀磁半导体能否实际应用的关键. 本文基于平均场理论的海森堡模型对Sc1Sn15O32和Sc1Sn15O31两种磁性结构的居里温度进行计算，公式如下[19]：

(2)

式中kB为玻尔兹曼常数，ΔE近似等于反铁磁基态与铁磁基态的能量差，通过人为设置所有原子的自旋方向(反铁磁基态：以Sc原子为原点截取xoy面，平面上方原子自旋向上、平面下方原子自旋向下，平面内原子无自旋；铁磁基态：xoy平面上下原子均自旋向上；各原子初始磁矩由软件自行优化获得)并计算体系的基态能量获得. 计算结果：ΔESc1Sn15O32=EAFM-EFM=0.053 eV；ΔESc1Sn15O31=EAFM-EFM=0.044 eV. 带入公式(2)得出两种磁性结构的居里温度分别为409.89 K和340.31 K，表明Sc掺杂SnO2体系能够实现室温铁磁性.

4 结 论

采用第一性原理方法，计算了Sc掺杂和Sc掺杂与O空位共存的SnO2超胞的电子结构和磁学性质. 结果表明，Sc掺杂能够诱导SnO2晶格中出现未配对的O-2p态电子，这个弱束缚电子的自旋极化使SnO2具有铁磁性，在一定Sc掺杂浓度范围内，体系的净磁矩随Sc掺杂量线性增加. SnO2中的O空位能够诱导产生未配对Sn-5p态电子，该电子的自旋极化也能为SnO2体系贡献净磁矩，但未配对Sn-5p和O-2p态电子态电子分别由电离施主和受主诱导产生，因此二者之间存在补偿效应，可能引起SnO2体系出现磁性猝灭. 居里温度的计算结果表明Sc掺杂SnO2能够实现室温铁磁性. 与前人的研究类比，本文提出了SnO2稀磁半导体中潜在的磁性猝灭机制，这对此类稀磁半导体的进一步实验研究具有重要的理论指导意义.