基于密度泛函理论的单层氢化石墨烯特性分析

汪杰君， 张 存， 王方原， 甘永莹， 李 树

(1.桂林电子科技大学 电子工程与自动化学院， 桂林 541004; 2.桂林电子科技大学 广西光电信息处理重点实验室， 桂林 541004;3.桂林电子科技大学北海校区 海洋工程学院， 北海 536000)

1 引 言

石墨烯具有六边形对称的二维蜂窝状晶格[1]. 由于其非凡的电，热和机械性能，它在纳米复合材料和纳米电子设备中具有巨大的应用潜力[2-6]. 自从首次分离出单层石墨或石墨烯以来，大量致力于这种独特材料性质的研究. 石墨烯因其无能带结构而具有点状费米面和费米能级的线性色散而备受关注. 这些性质使得我们在石墨烯中观察到弹道运输，狄拉克型准粒子和石墨烯中的异常量子霍尔效应等[7]. 并且石墨烯出色的电子迁移率使其具有在电子，能源和生物技术等许多领域中应用的潜力[8-17]. 此外，这种半金属膜的几乎透明的光学性质使其成为用于光电器件例如太阳能电池的良好候选材料[18].

Oil等人通过使用Hartree-Fock方法以及密度泛函理论研究了不同尺寸H-graphene的基态能量，发现随着C原子数的增加基态能量也随之增加[19]. 但是并没有研究尺寸与稳定性以及电子性质的关系. 而Karki等人系统的研究了尺寸与H-graphene团簇稳定性关系，发现尺寸与团簇稳定性呈现正相关[20]. 到目前为止，人们对于不同尺寸H-graphene的激发态分析较少，由于激发态研究对H-graphene的光学性质分析具有重要意义，为此我们进行了一系列关于不同尺寸H-graphene的详细计算，研究不同尺寸H-graphene的稳定性、HOMO-LUMO能隙以及电子激发态.

在目前的工作中，利用量子化学计算软件，对不同尺寸H-graphene的结构稳定性、HOMO-LUMO能隙以及电子激发态进行了研究. 其中H-graphene是由16-126个碳原子组成并且边界由H原子终止的矩形H-graphene团簇，这些研究结果将有助于研究人员对不同尺寸H-graphene稳定性判断，通过分析HOMO-LUMO gap达到对H-graphene能隙的调整，以及对不同H-graphene光学特性的判断.

本文组织如下:在第2节中，我们简要介绍了计算方法. 在第3节中，我们展示了本研究的结果和讨论，结论将在第4节中给出.

2 计算方法

密度泛函理论(Density functional theory简称DFT)[21]是研究多电子体系电子结构的一种量子力学方法，是指体系的性质完全用密度泛函描述和确定，而不借助于体系波函数. 研究是基于密度泛函理论的第一性原理[22]，通过使用Gaussian16W量子化学计算程序[23]，运用密度泛函理论以及梯度校准函数B3LYP(Becke's 3-parameter hybrid exchange functional and Lee, Yang, and Parr correlation functional)[24]，对不同尺寸H-graphene团簇(包括C16H10，C30H14，C48H18，C70H22，C96H26，C126H30)进行了几何优化. 以优化结构为基础，分别计算不同尺寸基态时H-graphene团簇的体系总能量，分析HOMO-LUMO能隙以及不同尺寸H-graphene的激发态.

为了研究H-graphene的稳定性，我们使用Gaussian16W计算了单独C原子和H原子的基态能量为参考. 计算出不同尺寸H-graphene的结合能(Binding Energy)，以及比结合能(Specific Binding Energy). H-graphene的结合能通过下式计算：

Ebingding=nCEC+nHEH-EH-graphene

(1)

其中Ebinding是不同尺寸H-graphene的结合能，nC和nH是不同尺寸H-graphene中C原子和H原子的数量，EC和EH分别是单独C原子和H原子的基态能量，EH-graphene是相应的H-graphene基态能量. 不同尺寸H-graphene的比结合能定义为H-graphene的结合能除以相应的原子总数，比结合能通过下式计算：

(2)

其中Especific-binding表示不同尺寸H-graphene的比结合能.

3 结果与讨论

3.1 优化结果

通过使用DFT/B3LYP，对碳原子数分别为16、30、48、70、96和126，且边缘通过H原子终止的六个氢化石墨烯团簇进行了优化计算如图1， 且六个石墨烯团簇的原始C-C键长均为1.42 Å，键角为120°，C-H键长均为1.10 Å，键角为120°. 优化之后，每个石墨烯团簇C-H键长最大均为1.085 Å，最小均为1.084 Å，而C-C键长变化较大，对于C16H10团簇C-C键长最大为1.440 Å，最小为1.361 Å；C30H14团簇C-C键长最大为1.449 Å，最小为1.355 Å；C48H18、C70H22、C96H26和C126H30团簇C-C键长最大均为1.354 Å，最小键长均为1.451 Å. 由此可以看出C-H键长相较于团簇尺寸变化较小，而C-C键长相较于团簇尺寸变化较大，但是随着尺寸增大，C-C键长的变化趋于稳定. 此外，对于优化之后不同键角的变化均小于2°.

图1 各个石墨烯团簇的几何结构(a) C16H10，(b) C30H14，(c) C48H18，(d) C70H22，(e) C96H26，(f) C126H30Fig. 1 The geometries of various graphene clusters(a) C16H10，(b) C30H14，(c) C48H18，(d) C70H22，(e) C96H26，(f) C126H30

3.2 稳定性

为了研究不同尺寸H-graphene的稳定性，我们通过使用DFT/B3LYP，对六个C16H10、C30H14、C48H18、C70H22、C96H26和C126H30的H-graphene团簇分别进行了单点能计算. 其中我们以C原子的基态能量-1022.412 eV，H原子的基态能量-13.533 eV为参考，计算了H-graphene的结合能以及比结合能，见表1.

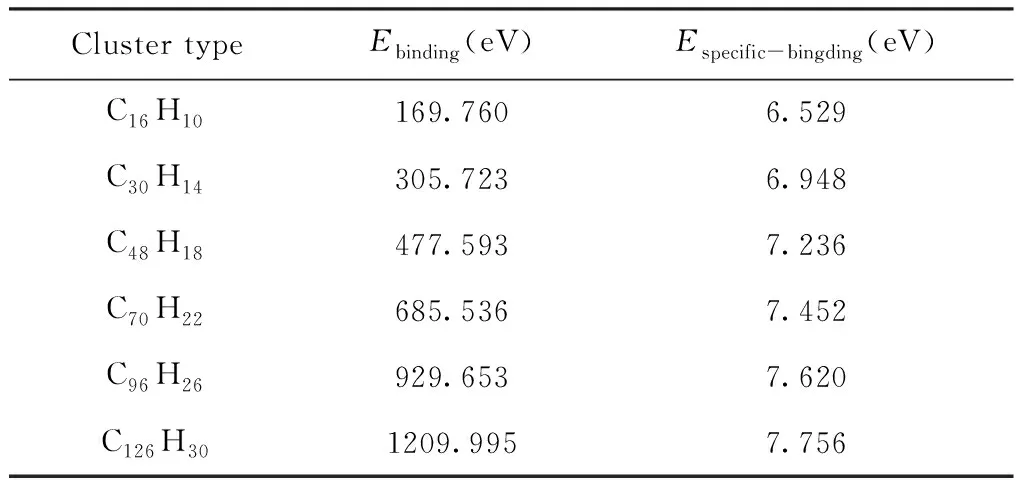
表1 石墨烯团簇的结合能 (Ebinding) 以及比结合能 (Especific-binding)

从表1中可以看出，随着H-graphene的尺寸的扩大，结合能与比结合能也随之增大，也就意味着大尺寸H-graphene比小尺寸更加稳定. 此外C96H26相比C16H10的比结合能增长21.7%，而C126H30相比C16H10的比结合能增长23.9%. 比结合能随着H-graphene尺寸增加而增加，在C96H26之后逐渐趋于饱和. 换句话说，大尺寸H-graphene比小尺寸更加稳定.

3.3 HOMO-LUMO能隙

我们计算分析了不同尺寸的H-graphene的最高占据分子轨道(HOMO)和最低未占据分子轨道(LUMO)的能隙值,并给出了曲线图，如下图2所示.

图2 不同尺寸H-graphene团簇的HOMO-LUMO轨道能隙值Fig. 2 HOMO-LUMO orbital energy gaps of H-graphene clusters of different sizes

在本工作中，我们利用自然键轨道分析(NBOs)系统地研究了H-graphene团簇的HOMO-LUMO能隙变化与结构稳定性的关系. HOMO-LUMO能隙值随着H-graphene团簇尺寸的变化如图2所示. 从图2中可以看出，HOMO-LUMO能隙值随着H-graphene团簇尺寸的增加而减小. 在较小尺寸的H-graphene中，由于量子效应起主要作用，因此出现了较大的HOMO-LUMO能隙. 随着H-graphene团簇尺寸的增加，量子效应的作用逐渐减小，因此较大尺寸的H-graphene团簇的HOMO-LUMO能隙变化不明显. 从这个分析可以看出，对于无限大的H-graphene团簇中，HOMO-LUMO能隙无限趋近于零(相当于零带隙)，其电子性质与纯石墨烯相似.

3.4 电子激发分析

为了更好的了解不同尺寸H-graphene的光学性质，我们选取了具有较大振子强度且在吸收过程中起着至关重要的作用的主要激发态，并分析主要激发态与之相对应的跃迁情况. 表2列出了C16H10、C30H14、C48H18、C70H22四个石墨烯团簇的主要激发态的激发波长、激发能以及过渡系数.

表2 不同尺寸H-graphene的主要激发态的激发波长、激发能以及过渡系数

从表2中可以看出，其中C16H10的S8激发主要由H-2→L+2(3.38%)，H-1→L+1(89.78%)，H→L(5.78%)组成，其中H和L分别表示HOMO和LUMO轨道，括号内的百分比数据表示轨道跃迁贡献. 随着H-graphene团簇的扩大主要激发态的激发波长变长且激发能不断降低. 并且不同尺寸的H-graphene的跃迁轨道是不同的，反应了尺寸对H-graphene团簇光学性质的影响.

图3为不同尺寸H-graphene在酒精溶剂中的紫外-可见吸收光谱. 从中可以看出随着H-graphene尺寸增加，2×2尺寸的H-graphene在可见光吸收区域不明显，在紫外区具有较强的吸收然而对于3×3，4×4和5×5尺寸的H-graphene，吸收峰随着尺寸的增大而逐渐移出紫外吸收区，并且5×5尺寸的H-graphene吸收峰已经完全移出紫外吸收区.

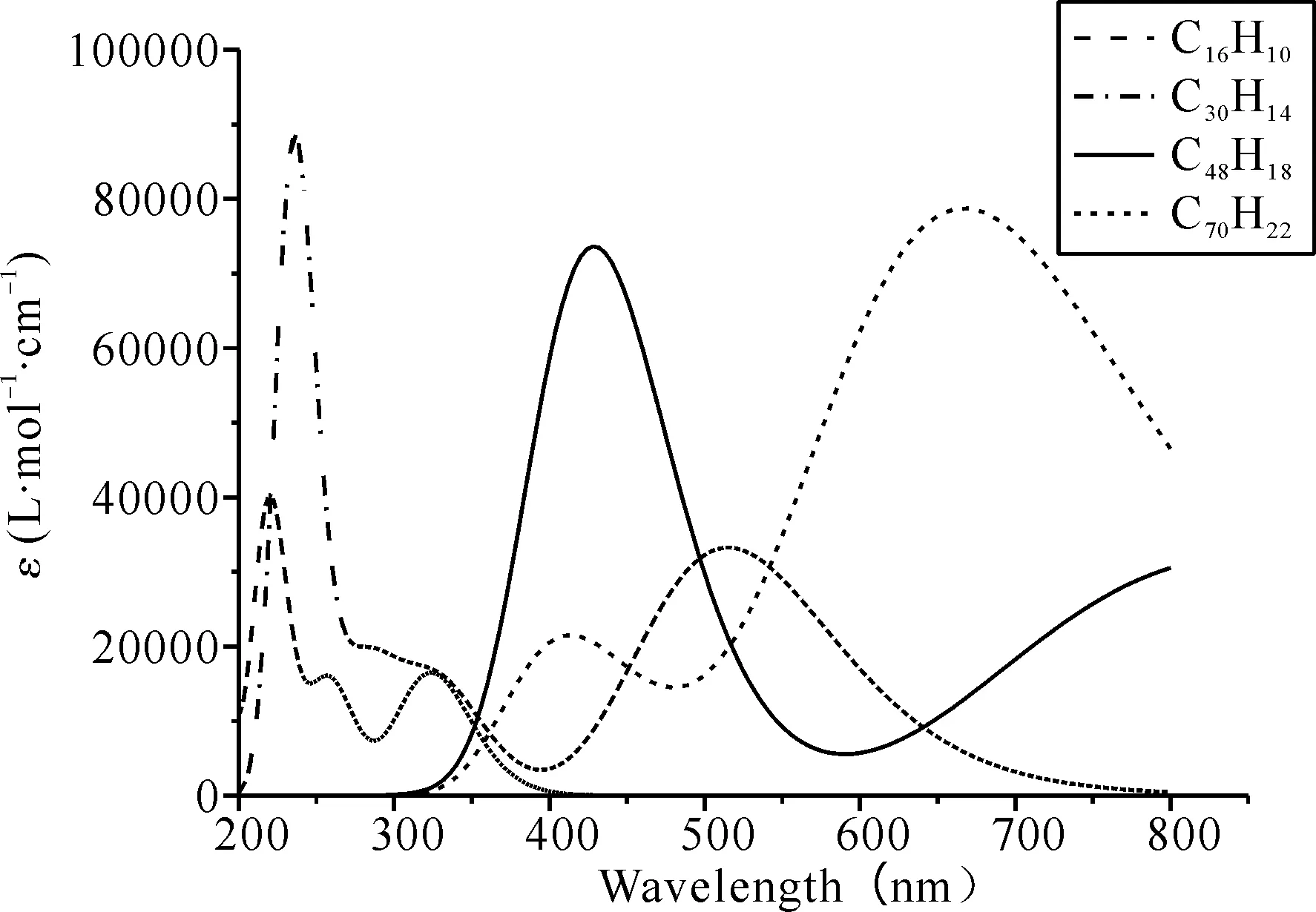
图3 不同尺寸H-graphene的紫外-可见吸收光谱Fig. 3 Ultraviolet-visible absorption spectra of H-graphene of different sizes

4 总 结

本文研究了不同尺寸的石墨烯量子点的结构稳定性与吸收光谱. 通过使用Gaussian优化并计算出不同尺寸H-graphene的基态能量，利用基态能量算出不同尺寸H-graphene的比结合能. 计算表明，随着H-graphene的尺寸的扩大，结合能与比结合能也随之增大，也就意味着大尺寸H-graphene比小尺寸更加稳定. 对不同尺寸H-graphene团簇的HOMO-LUMO研究发现，HOMO-LUMO能隙值随着H-graphene团簇尺寸的增加而减小. 利用优化之后的H-graphene结构并计算并分析激发态，发现随着尺寸的增加紫外-可见吸收光谱出现红移现象.