基于散列技术的多层关联规则算法的改进

郭 倩，殷丽凤

(大连交通大学 软件学院，辽宁 大连 116028)

0 引 言

自从Agrawal等[1]提出挖掘关联规则Apriori算法以来，众多学者针对此算法有较多冗余项集、很大的I/O负载的缺点做了不断改进，如周发超等[2]针对Apriori算法中的I/O过载大的问题，提出了一种I_Apriori算法来提高算法效率；孙学波等[3]基于Hadoop平台，采用HBase文件存储系统对海量数据分布式存储以及MapReduce框架进行分布式计算，来实现Apriori数据挖掘算法。

随着数据量的增加，在分析分类特征数据时，发现不同层之间也存在关联规则，而Apriori算法只适合对单层数据挖掘关联规则，针对这一需求，国内外研究学者进行了多层关联规则算法的研究。Stri_kant等[4]对Apriori算法进行了改进，提出了经典的多层关联规则Cumulate算法；李进等[5]提出能够在层次树上的各个抽象层进行的多层关联规则；袁冬菊[6]提出基于FP_Growth的约束事务扩展的多层关联挖掘算法；何晴[7]提出基于聚类的多层关联规则算法，运用K-means算法与Apriori算法相结合来解决多层关联规则的问题；于茜[8]提出基于粒度的多层关联规则算法，使用粒计算进行分层并且基于粒度计算支持度与置信度在农业中进行应用研究；蒋涛等[9]提出将K-means算法与Apriori算法结合的多层关联规则来分析山洪成因的问题；邓晓衡等[10]提出基于层次分析法(AHP)和混合Apriori-Genetic的模型。

Cumulate算法继承了Apriori算法的缺点。本文对Cumulate算法产生不必要冗余项集的缺点进行改进，首先将带有子孙关系的频繁1项集在生成候选2项集的过程中直接跳过，不生成此类候选2项集；其次将候选2项集映射到散列表中，将对应统计数小于支持度阀值的桶删掉。通过上述两个步骤来搜索频繁项集，通过实例分析和实验验证改进后的算法具有较高的执行效率。

1 预备知识

本文需要关联规则、散列技术的基本概念以及Cumulate算法思想。其中关联规则和散列技术的具体概念请参见文献[11]，Cumulate算法是较为经典的多层关联规则算法，该算法主要是对单层关联规则Apriori算法进行改进得来的，其具体思想和优化措施参见文献[4]。

2 基于散列技术的Cumulate算法

为了克服多层关联规则Cumulate算法的缺点，本节对此算法进行了改进，改进思想如下：

(1)原算法是在生成候选集之后进行判断子孙关系进行筛选，本算法是在生成候选项集的过程中将具有子孙关系的冗余项直接删除。

(2)使用散列技术将候选2项集进行筛选。将候选2项集通过散列函数映射到散列表中，散列表中每个桶设置计数变量count，在映射之后，直接扫描桶中对应的count，将count小于最小支持度的桶删除，留在桶内的为新的候选2项集，再通过扫描事务集得到频繁2项集。改进后的算法称作Hash_Cumulate算法。

Hash_Cumulate算法的流程如图1所示。

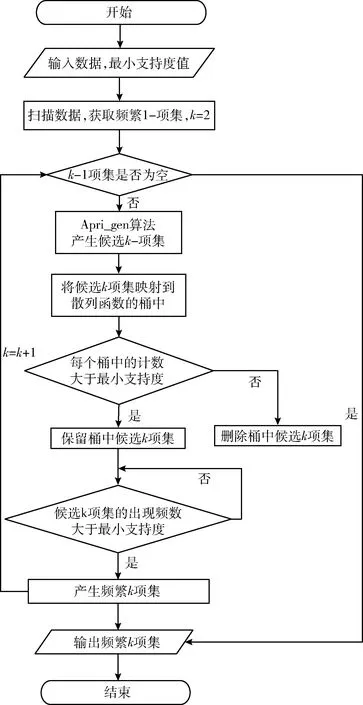
图1 算法流程

T表示事务数据库，Min_sup表示最小支持度，L表示T中的频繁项集。Hash_Cumulate算法伪代码如下：

算法Hash_Cumulate

输入：T：事务数据库。

Min_sup：最小支持度。

输出：L：T中的频繁项集。

主方法：

(1)T*=extenion(T); //将事务所有祖先添加进来L1:={frequent 1-itemsets}; //找到频繁1项集

k=2;

PruneTREE=L1;//将频繁1项集赋给剪枝的树

(2)While(Lk-1!=∅)do {

(3)Ck=apriori_gen(Lk-1,k) //生成候选集

(4) If(k=2)then{

Ck=hash_candidate(Ck,Min_sup)//改进(2)

}

(5)PruneTREE=cutTree(Ck,PruneTREE)//更新概念树

(6) for each transcationst∈Tdo {

(7) for each itemx∈tdo{

ancestor=extentionOne(x);//获取x的祖先

}

(8) for each candidatec∈Ckdo{

If(c∈ancestor)then{

c.frequence++; //得到候选集c的频数

} }

(9)Lk={x∈Ck|x.frequence≥Min_sup)}//频繁项集

k:=k+1; }

(10)returnL=∪kLk;

下面的extenion算法描述将事务数据库T中的事务的所有祖先添加到事务集T*中。

Procedure extenion(T)

(1)for each 事务t∈Tdo{

(2) for each 项x∈tdo{

Temp=findancestorforx; //找到项x的祖先

}

InserttemptoT*//将找到的祖先插入T*

}

(3)returnT*;

下面的apriori_gen算法描述将频繁k-1项集生成候选k项集，其中Lk-1表示频繁k-1项集，k表示当前候选集的长度。

Procedure apriori_gen(Lk-1,k){

(1) for each 项集s1∈Lk-1

(2) for each 项集s2∈Lk-1{

//改进(1), 若为子孙关系，直接跳过该循环

(3) If(k=2){

(4) If(s1,s2∈子孙关系)break；

(5) }

(6) If(s1[1]=s2[1])∧(s1[2]=s2[2])…∧

(s1[k-2]=s2[k-2])∧(s1[k-1]<

s2[k-2])then{

(8) If has_infrequent_subset(z,Lk-1)then

(9) Deletez;//剪枝步：删除非频繁项集

(10) else addztoCk;

(11) }

}

(12)returnCk;

本算法调用了判断子集是否为频繁项集的算法has_infrequent_subset(z,Lk-1)(其中z表示候选k项集，Lk-1表示频繁k-1项集)。has_infrequent_subset的伪代码参见文献[11]。

下面的hash_candidate算法将候选2项集映射到桶中，其中Ck表示候选k项集，Min_sup表示最小支持度阀值。

Procedure hash_candidate(Ck,Min_sup)

(1)for eachc∈Ck{

(2) for eachl1，l2∈c{

//通过散列函数映射到对应桶中

h.num=hash(order(l1),order(l2))

h.count++;

Insertctoh.content;

}

InserthtoH

}

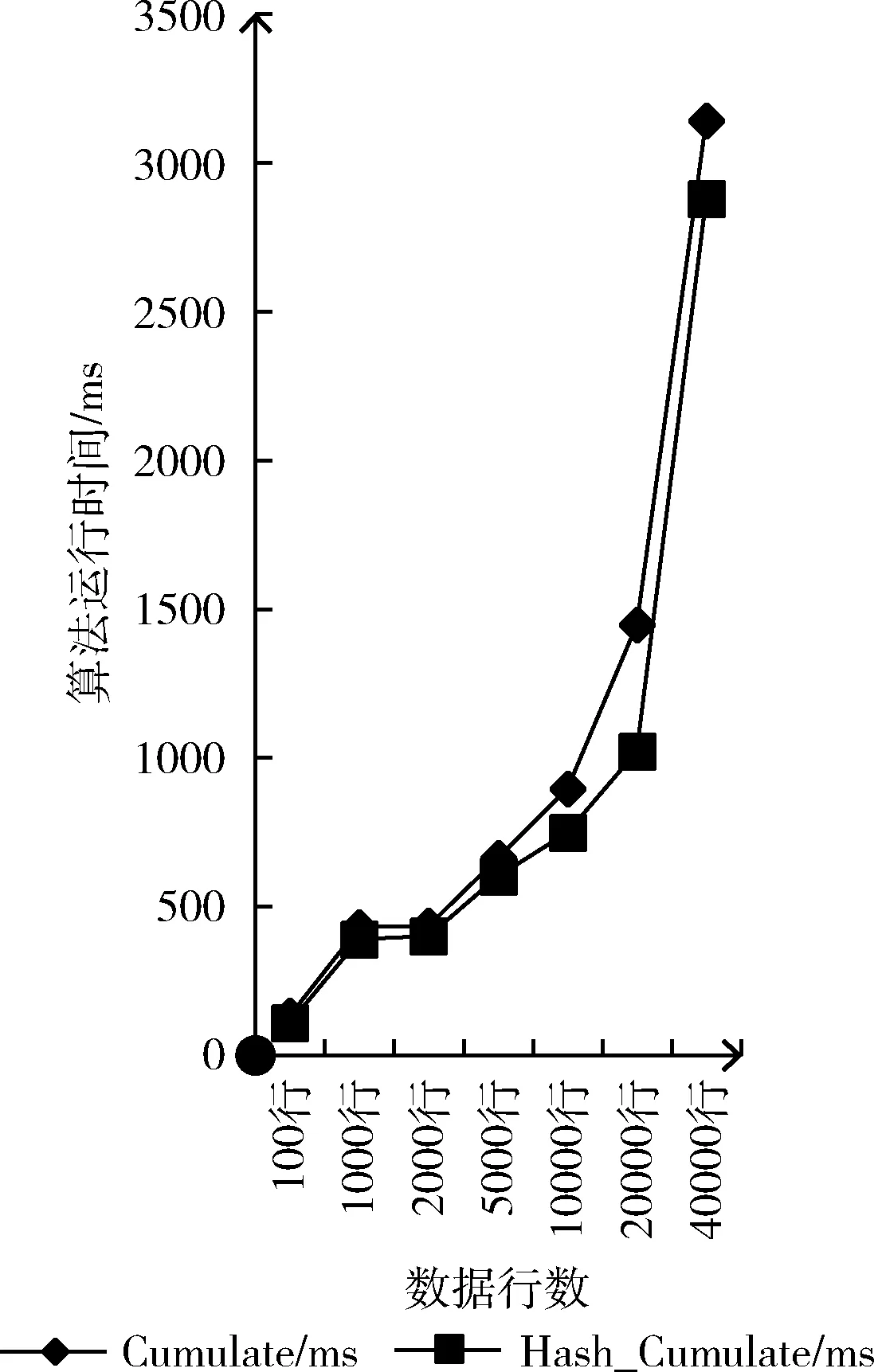
(3)for eachh∈H

//将桶中小于最小支持度的项集删掉

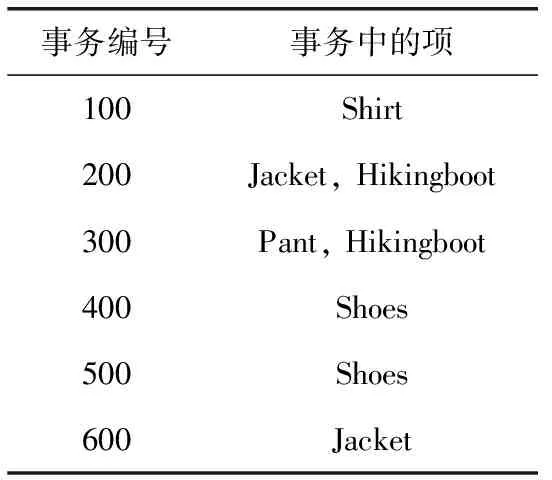
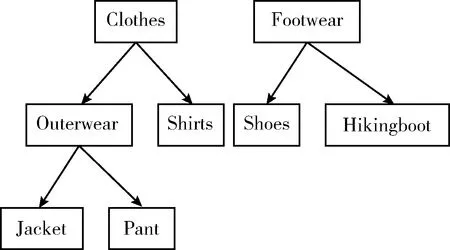
If(h.count

(4)returnH;

下面的cutTree算法用候选集来剪枝，其中Ck表示候选k项集，PruneTREE表示剪枝树，newPruneTREE表示剪枝之后的树。

Procedure cutTree(Ck，PruneTREE)

(1) for eachtree∈PruneTREE

(2) for eachc∈candidate

If(tree∈c)then

//把候选集中存在的项放到新概念树中

InsertctonewPruneTREE

(3)returnnewPruneTREE;

下面的extentionOne算法描述项的祖先，x表示事务集中的项，Temp表示x的祖先。

Procedure extentionOne(x)

(1)returnTemp=findancestorforx;

算法性能分析:算法Hash_Cumulate是正确的，其时间复杂度为O(x3)，m为事务集中的事务数，n为某事务中项的数量，z为能产生的频繁项集的最大长度，频繁k-1项集的数量为x，候选k项集的数量为y。

证明：正确性。算法Hash_Cumulate是通过步骤(3)和步骤(4)对Cumulate算法进行改进。步骤(3)对应生成候选集的函数apriori_gen，apriori_gen的步骤(3)完成Hash_Cumulate算法改进(1)，即在寻找频繁2项集过程中，对生成候选2项集的过程改进，在生成候选2项集过程中判断两项是否具有子孙关系，将具有子孙关系的两项跳过。Hash_Cumulate中的步骤(4)对应hash_candidate，hash_candidate将候选2项集进行散列映射筛选出新的候选2项集，从而减少冗余候选2项集，完成算法思想改进(2)，满足Hash_Cumulate算法思想，所以算法是正确的。

时间复杂度分析:本算法的时间复杂度主要由主方法的步骤(1)和步骤(2)决定，(1)的执行次数由extenion算法中的双重循环决定，其中外层循环extenion算法中的(1)的执行次数由事务集中的事务数m决定，extenion算法中的内层循环(2)的执行次数由事务中的项数n决定，所以主方法的(1)的执行次数为m×n。主方法的(2)的执行次数是由(2)本身及其内部的循环决定，(2)本身的执行次数由算法能找到的频繁项集的最大长度z决定，内部循环包括步骤(3)、步骤(4)和步骤(6)，主方法的步骤(3)的执行次数由apriori_gen函数中的双重循环决定，其中外内层循环apriori_gen函数中的(1)、(2)的执行次数都由频繁k-1项集的数量x决定，内层循环apriori_gen函数中的(2)包括has_infrequent_subset算法，它的执行次数也由频繁k-1项集的数量x决定，所以主方法的步骤(3)的执行次数为x3；主方法的步骤(4)由算法hash_candidate决定，它的执行次数由候选k项集的数量y决定；主方法的步骤(6)循环嵌套两个内层循环，即主方法的步骤(7)和步骤(8)，主方法的步骤(6)的执行次数由事务集中的事务数量m决定，主方法的步骤(7)的执行次数由事务中的项的数量n决定，主方法的步骤(8)的执行次数由候选k项集的数量y决定，所以主方法的步骤(6)的执行次数为m×n+m×y。综上所述，本算法的执行次数为m×n+z×(x3+y+m×n+m×y)，通常情况下，z和n远小于x，m和y略大x，所以算法时间复杂度为O(x3)。

3 实例分析

本节通过实例对Cumulate算法和Hash_Cumulate算法进行分析，说明Hash_Cumulate算法较好的原因。表1给出某商场销售事务数据库D，D中包括6个事务，设最小支持度为2，置信度为60%。

表1 事务数据库D

通过分析表1发现项间是有层次的，对表1的事物集重新进行概念分层，得到事务表分层如图2所示。

图2 事务分层

步骤1 算法先将事务表D扩展，将每一项的祖先全部添加进去，计算每一项及其祖先的支持度，得到满足最小支持度为2的频繁1项集，见表2。

表2 频繁1项集及其支持度

步骤2 进行连接剪枝，得到候选2项集，见表3。

步骤3 判断表3中项集中项的关系，如果是祖孙关系，则删除该候选2项集。进行这次筛选后得到的结果见表4。

表3 候选2项集

步骤4 在候选集中不包含的项但事务集中包含的项，在事务集中需删除。由表4候选集可知，在事务集中删除项{Pant}、{Shirt}。

表4 筛选后的候选2项集

步骤5 进行最小支持度筛选后，得到频繁2项集见表5。

表5 频繁2项集

步骤6 由于找不到频繁3项集，算法终止。

步骤7 根据置信度来得到关联规则见表6。

表6 关联规则

Hash_Cumulate算法步骤如下：

步骤1 同上。

步骤2 候选2项集中不能包含有子孙关系项，所以将这些候选项在存在子孙关系的项 {{Clothes，Jacket}，{Clothes，Outerwear}，{Jacket，Outerwear}，{Hikingboot，Footwear}，{Hikingboot，Shoes}} 直接跳过，这样直接节省部分保存候选2项集的空间，改进后的步骤2直接得到的候选集见表4。

步骤3 选择散列函数为：hash(x,y)=(order(x)×4+order(y))mod prime(k), 其中order(x)表示x在项集中的编号，order(y)表示y在项集中的编号，prime(k)返回在k范围内最大的素数，k表示事务集中的事务数，例如：在频繁1项集中Clothes的编号为1，Shoes的编号为6，事务数为6，6的范围内最大素数是5，所以带入哈希函数得到桶地址为0，则将候选2项集{Clothes，Shoes}放入桶地址为0的桶中。将所有候选2项集散列映射到桶中，产生冲突的候选项放入桶中并增加对应的桶计数见表7，最后将计数小于最小支持度的桶内的项删除，即将桶地址为0中的候选2项集删掉，桶中剩余的候选2项集即桶1、2、3、4中的候选2项集与事务集进行比较，产生频繁2项集，通过这个方法减少2项集的数量，最终得到候选2项集见表8。

表7 散列表

表8 筛选后的候选2项集

步骤4～步骤7与上述未改进时相同，最后根据相同的置信度60%得到的关联规则也如表6所示。

通过上述实例分析，上述改进主要是对候选2项集进行缩减，从改进算法的步骤2可以直接得出原来Cumulate算法的步骤3所得的结果，可以看出改进算法的优越性，从表8中可以看出候选2项集对比之前确实减少了，从而缩短算法运行时间，实例证明该改进确实将候选2项集的个数减少，提高算法运行效率。

4 Hash_Cumulate算法的实验及性能分析

为对比分析Hash_Cumulate算法与原始Cumulate算法的运行效率，将这两种算法在相同的数据记录下的执行时间进行比较。

实验环境：操作系统为Windows 7，64位，内存容量为8 G，测试工具为MyEclipse2014，语言为JAVA，采用模拟数据IBM数据集T10I4D100K进行测试，设置最小支持度为0.2。

(1)本实验将已经处理好的数据对两种算法进行运行时间的比较。分别对相同的多条事务处理的时间比较见表9，其中k表示1000。

表9 实验结果对比

为更清晰展示算法时间的对比，时间的折线对比如图3所示。

图3 时间对比

(2)在算法空间上分析比较。在算法思想改进(1)中，在未生成候选2项集之前判断其子孙的关系，从而将不存在子孙的关系的候选2项集进行存储，节省了之前存储冗余2项集的空间。在支持度为0.2情况下，事务为10 000条，事务的最大层数为3层，若频繁1项集有3000个，则最多约可节省的空间为12 000个字节。

(3)实验进行了算法准确率的比较，算法的准确率比较结果见表10。

表10 算法准确率

5 结束语

本文针对Cumulate算法存在的问题，提出了减少冗余候选2项集的改进算法，首先在候选2项集生成的时候判断其关系，并且在生成候选2项集之后将散列技术应用于筛选候选2项集，从而减少候选2项集的数量。将改进的算法和原始算法在性能上比较和分析，发现改进算法从时间和空间上都具有良好的性能。在未来，将引进多维算法，实现多维多层的关联规则算法。