考虑动态拥堵的多车型绿色车辆路径问题优化
2021-09-16狄卫民杜慧莉张鹏阁
狄卫民,杜慧莉,张鹏阁
(郑州大学 管理工程学院,河南 郑州 450001)
0 引 言
在规划配送车辆路线时,既要追求经济目标,又要注重环境影响[1],因此,绿色车辆路径问题(green vehicle routing problem,GVRP)引起了学者们的关注。Li等[2]、张亚明等[3]和段凤华等[4]研究了多车型GVRP问题,结果表明多车型配送有利于碳减排,但是这些学者均未考虑配送过程中的道路交通状况。近些年来,城市道路拥堵问题日益突出,Xiao等[5]、徐梅等[6]和周鲜成等[7]在GVRP问题中考虑了道路拥堵因素,但尚未涉及多车型配送的情形。赵志学等[8]虽然综合考虑了道路拥堵、碳排放、多车型与时间窗,但仅以静态区域来描述拥堵状况,车辆行驶速度仅与所处的区域有关,未涉及考虑时变速度的动态GVRP。
本文在已有研究的基础上,将配送服务时间划分为若干时段,并以道路拥堵系数反映不同时段的道路拥堵状况;分析速度、距离、载重和车辆类型对碳排放的影响,建立了以系统总成本最小化为目标的非线性规划模型。根据模型特点,设计了头脑风暴优化算法(brain storm optimization,BSO),通过算例验证了模型和算法的有效性。
1 问题描述与假设
1.1 问题描述
考虑动态拥堵的多车型GVRP可描述为:配送中心派遣多种车辆为若干客户送货,已知每种车辆的负载能力、启动成本和单位运输成本。车辆从配送中心出发,为客户服务后返回配送中心。客户具有时间窗要求且服务时间已知,每个客户仅由一台车服务。不同时段的道路拥堵程度不同,道路拥堵影响车辆行驶速度和行驶时间。配送车辆的碳排放量与车辆自身状况和道路拥堵程度有关。本文要解决的主要问题是:为使配送系统的总成本最小,应如何确定配送车辆的类型和数量?如何安排各车辆的配送路径?
1.2 假设条件
为方便模型构建,提出以下假设:①同一时段内车辆行驶速度恒定,不同时段的车辆行驶速度不同;②仅考虑单一产品的配送;③配送中心和客户的位置已知,各节点间距离已知;④客户必须全部被服务,并且每个客户只允许访问一次;⑤客户的需求量已知,且小于车辆的最大负载能力;⑥车辆需在客户规定的时间窗内完成配送任务,车辆提前或者延迟到达均要承担相应的惩罚。
2 模型构建
2.1 符号与变量
G=(N,R)为配送网络,N为节点集合,N={0,1,2,…,n},其中,0代表配送中心,N0={1,2,…n} 代表客户;R为节点间的弧集,R={(i,j)|i,j∈N,i≠j};L为车型集合,L={1,2,…,l};K为某类型车辆的编号集合,K={1,2,…,k};T为配送服务时间的长度,T={T1,T2,…,Th,…,TM} 表示将T划分为M个时段;Zl为l类型车辆的数量;fl为l类型车辆的启动成本;cl为l类型车辆的单位运输成本;qi为客户i的需求量;Ql为l类型车辆的最大负载能力;dij为弧(i,j)的长度;rh为Th时段的道路拥堵系数,1≤rh≤10,取值越大表示拥堵状况越严重;v为车辆在道路畅通状况下的行驶速度;λ为消耗每千克CO2的环境成本;Ai为违反客户i规定时间窗的惩罚成本;si为客户i的服务时间;[ETi,LTi]为客户i规定的时间窗。

2.2 拥堵状况下车辆行驶时间分析
道路拥堵系数是指平均一次出行实际旅行时间与自由流状态下旅行时间的比值,可通过百度地图获取。本文使用的道路拥堵系数以近七日同时段道路拥堵系数的平均值表示。由于一天内城市交通状况呈规律性变化,因此车辆行驶速度具有明显的时间相关性[9]。定义车辆在时段Th=[th,t′h]内的行驶速度为vh,则有
(1)
t′h=th+1
(2)


(3)
当1≤p≤M-h时
(4)

(5)
(6)

(7)
(8)
当g∈[0,p-1]时
(9)
否则,当g∈[p+1,M-h]时
(10)
式(5)、式(7)、式(9)和式(10)计算了不同情形下车辆在每个时段内的实际行驶距离;式(6)、式(8)计算了不同情形下车辆的行驶时间。
2.3 碳排放量的计算
一般情况下,运输车辆在行驶过程中必然会产生碳排放,碳排放量与车辆行驶速度、距离、载重及车型有关。本文采用欧盟委员会在MEET报告中给出的碳排放计算函数[10]来刻画碳排放量。
假设车辆在时段Th从节点i出发驶向节点j,途径时段Th+g内产生的碳排放量可用式(11)表示
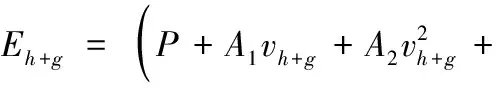

(11)
此公式仅适用于计算空载车辆在平缓道路上行驶时产生的碳排放量(单位:克)。
然而,车辆在配送过程中的载重不可能完全为零,因此,Mansoureh等[11]在MEET模型的基础上考虑了载重约束进行修正。载重约束的计算公式为


(12)

因此,车辆在弧(i,j)上产生的碳排放量为
(13)
2.4 数学模型
由上述分析,构建的考虑动态拥堵的多车型GVRP的非线性规划模型如下
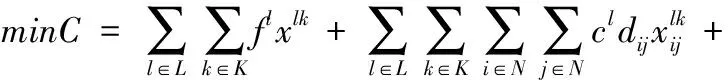


(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
xlk={0,1}, ∀l∈L, ∀k∈K
(24)
(25)
(26)
式(14)为目标函数,表示由车辆启动成本、运输成本、碳排放成本和违反时间窗的惩罚成本构成的系统总成本最小。式(15)为车辆载重约束,表示该车辆服务的客户的总需求量不得超过车辆负载能力;式(16)保证每个客户仅能由一辆车提供服务;式(17)表示使用某类型的车辆总数不得超过该类型车辆的原有数量;式(18)确保每个客户只服务一次;式(19)表示车辆为客户服务后必须离开;式(20)保证车辆从配送中心驶出并在完成配送任务后返回配送中心;式(21)表示车辆在零时刻从配送中心驶出;式(22)、式(23)分别为到达和离开客户的时间约束;式(24)~式(26)为决策变量取值约束。
3 算法设计
考虑动态拥堵的多车型GVRP是VRP的延伸,属于NP-hard问题,精确算法无法避开指数爆炸的问题,只适合求解小规模问题,对大规模问题难以求得最优解,而元启发式算法在求解此类问题上效果较好[12]。BSO算法是在模拟人类头脑风暴过程的基础上形成的一种群体智能算法,头脑风暴过程的每个想法代表解集合中的一个个体,通过聚类方法分析解集合构成,基于解的分布生成新个体,经过不断迭代,得出满意解[13]。BSO算法对初始值没有要求,具有极强的全局搜索和快速收敛能力,因此,本文使用BSO算法求解考虑动态拥堵的多车型GVRP模型。BSO算法的具体步骤如下:
步骤1 生成初始种群
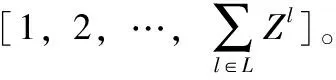
步骤2 计算适应度值
对初始种群中的每个个体以车辆载重和客户规定的时间窗进行检验。若该车辆服务的客户需求总量不超过车辆载重量,则此路线成立;若该车辆服务的客户需求总量大于车辆载重量,则按客户的服务顺序依次判断。例如,对于一条路线[1 2 3 4 5],若该车辆服务客户3时符合载重要求,一旦服务客户4则车辆超载,则规定该车辆在服务完客户3后返回配送中心,放弃服务客户4和5。对于放弃服务的每个客户,产生一个极大的缺货成本,表示未服务该客户产生的惩罚。然后依次计算相关联节点间的行驶时间及路段载重率,判断是否符合客户的时间窗要求,不符合要求的计算违反时间窗的惩罚成本。令个体的适应度值为车辆启动成本、运输成本、碳排放成本、违反时间窗的惩罚成本和缺货成本之和。
步骤3 聚类操作
用K-means聚类方法将种群中的个体聚成E类,并选择该类中适应度值最小的个体作为聚类中心。
步骤4 判断聚类中心是否被取代
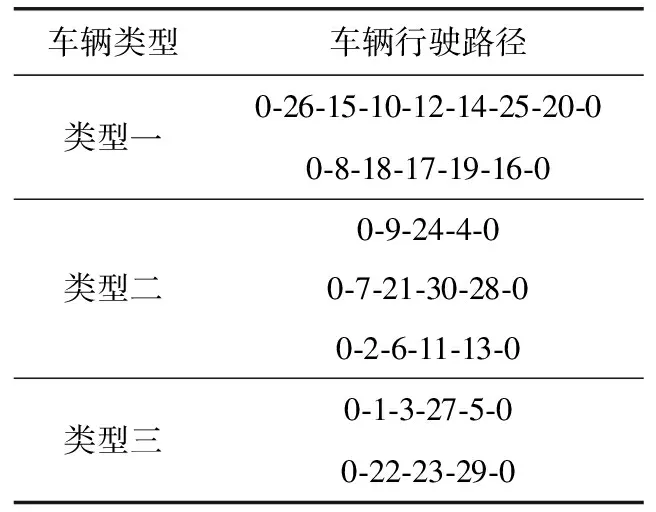
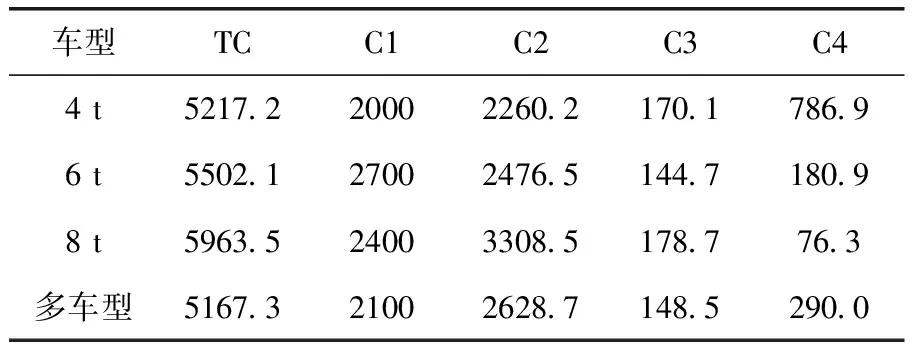
随机产生(0,1)之间的数,比较该值与给定概率P1的大小(0 步骤5 个体更新 在头脑风暴过程中,需要不断提出新的“想法”以期找出更优的决策方案,同理,BSO算法中使用在原个体上添加“随机扰动”的方式进行个体更新。BSO算法中添加“随机扰动”的方式为在原个体上加入高斯随机数,然而本文采用的编码方式为整数编码,不适用此方式。因此,本文采用遗传算法的交叉和变异操作作为个体更新的“随机扰动”。 首先,产生(0,1)之间的随机数Pb,并与给定的概率P2比较(0 (1)变异操作:若Pb (2)交叉操作:若Pb≥P2,随机选择两个类,并产生(0,1)之间的随机数Pd。对于给定的概率P4(0 步骤6 判断是否完成个体更新 若个体更新达到SIZE次,则完成个体更新,转入步骤7否则返回步骤5。 步骤7 判断是否满足停止条件 若算法已达到最大迭代次数,则算法终止,得到满意解;否则,转入步骤3。 BSO算法的流程如图1所示。 图1 BSO算法流程 本文使用一个随机生成的仿真算例来检验构建的模型和BSO算法。假设某地区有1个编号为0的配送中心和30个客户。客户的需求量、时间窗及服务时间见表1;节点之间的距离见表2;车辆的相关参数见表3。 表1 客户信息 表2 配送网络中部分节点之间的距离/km 表3 车辆参数 其余数据设置如下:消耗每千克CO2的环境成本λ=0.5元;违反客户规定时间窗的惩罚成本Ai=600元/h;未服务客户的缺货惩罚为10 000元/个;车辆在畅通路况下的行驶速度为40 km/h;配送服务时间长度为6∶00~13∶00,规定6∶00为配送服务开始的零时刻。根据城市道路拥堵情况,将配送中心的服务时间划分为6∶00~7∶00、7∶00~9∶00、9∶00~13∶00这3个时段,定义6∶00~7∶00、9∶00~13∶00为正常时段,道路拥堵系数r1=r3=1;7∶00~9∶00为早高峰时段,道路拥堵系数r2=2。 程序采用MATLAB R2014a编程实现,其中,在实验测试的基础上,BSO算法的参数设置如下:种群大小为100;最大迭代次数为200;聚类数目为5;概率P1、P2、P3、P4分别为0.2、0.8、0.4、0.5。 4.2.1 算例结果分析 将BSO算法在操作系统为Win 10,主频为2.7 Ghz的Intel Core i5 处理器上运行10次,平均运行时间为82.3 s。其中,最优运算结果的迭代趋势如图2所示。由图2可知,在第156代求得当前最优值5167.3,种群的最小成本和平均成本随着迭代次数增加均有明显的下降趋势,两者之间的差值逐渐减小,说明BSO算法能够有效求解该模型并且具有良好的收敛性。 图2 BSO算法迭代趋势 表4列举了图2对应的最优车辆行驶路径。结果表明,该配送中心共有7条配送路径,其中,使用2台类型一车辆、3台类型二车辆、2台类型三车辆。 表4 最优车辆行驶路径 4.2.2 算法有效性分析 遗传算法(genetic algorithm,GA)已被许多学者证明可以有效求解VRP问题,且应用较广[12],并且BSO算法中的个体更新方式使用了遗传算法的交叉和变异操作,于是本文使用GA与BSO算法进行对比。在实验测试的基础上,GA的设置如下:编码与解码方式与BSO算法相同,适应度函数设置为总成本的倒数,采用轮盘赌法进行选择,初始种群为100,最大迭代次数为200,交叉概率为0.7,变异概率为0.2。将GA程序运行10次,运行结果与BSO算法比较,见表5。 表5 BSO算法与GA的结果对比 由表5可知,BSO算法的最小目标值和平均目标值均小于GA,并且BSO算法的平均目标值较GA降低了19.19%,两者的运行时间差距不大,BSO算法比GA耗时多2.11%。通过对比可以看出,BSO算法的运算效果较好,且运算结果优于GA,验证BSO算法性能较好,可以有效求解本文研究的问题。 4.2.3 多车型与单车型配送对比 为验证多车型配送有利于降低成本,进行多车型与单车型配送的对比分析。针对此算例,假设配送中心分别采用4 t、6 t和8 t的单一车型进行配送服务,除车辆相关参数外,其余设置保持不变,使用BSO算法求解。将计算结果与图2最优值进行比较,见表6。其中,TC表示总成本;C1表示车辆启动成本;C2表示运输成本;C3表示碳排放成本;C4表示违反时间窗的惩罚成本(单位:元)。 表6 单车型与多车型配送成本对比 由表6结果可知:当仅使用4 t、6 t和8 t的单一车型进行配送时,总成本比多车型配送分别高出0.97%、6.48%和15.41%。因此,使用多车型进行配送服务是合理的。 4.2.4 考虑动态拥堵的GVRP与传统GVRP的对比 为验证在配送决策中考虑道路拥堵状况有利于降低配送成本,将本文研究的问题与传统GVRP进行对比。在本文的算例中去除道路拥堵系数这一参数,其余参数保持不变,于是,原问题变成车速确定的GVRP,使用BSO算法予以求解。将求得的最优配送路径带入考虑动态拥堵的GVRP,计算在未提前考虑交通状况时,一旦发生拥堵的配送成本。表7显示了考虑动态拥堵的GVRP与传统GVRP的结果对比。其中,各参数的含义与表6相同。 表7 考虑动态拥堵的GVRP与传统GVRP的结果对比 表7数据表明,传统GVRP求得的配送路径在拥堵状况下的各项成本都高于图2结果,且总成本比考虑动态拥堵的GVRP高出7.10%。因此,在优化配送路径时考虑道路拥堵可以有效减少配送费用,更具经济效益。 配送车辆的碳排放会对环境造成影响,物流企业应该引起高度重视。本文研究了考虑动态拥堵的多车型GVRP,将道路交通状况、碳排放、多车型及时间窗融入配送车辆路径优化中,使用时变速度描述道路拥堵状况,确定了道路拥堵状况下的车辆行驶时间,并引入碳排放计算公式,建立了以系统总成本最小化为目标的数学模型。由于该模型是非线性规划模型,根据其特点,设计BSO算法,通过算例及与遗传算法的对比验证了模型及算法的有效性。研究结果表明,在优化配送车辆路径时考虑动态拥堵及车型因素有利于降低配送成本。期望本文能为企业绿色配送和碳减排提供决策参考。
4 算例分析
4.1 仿真数据
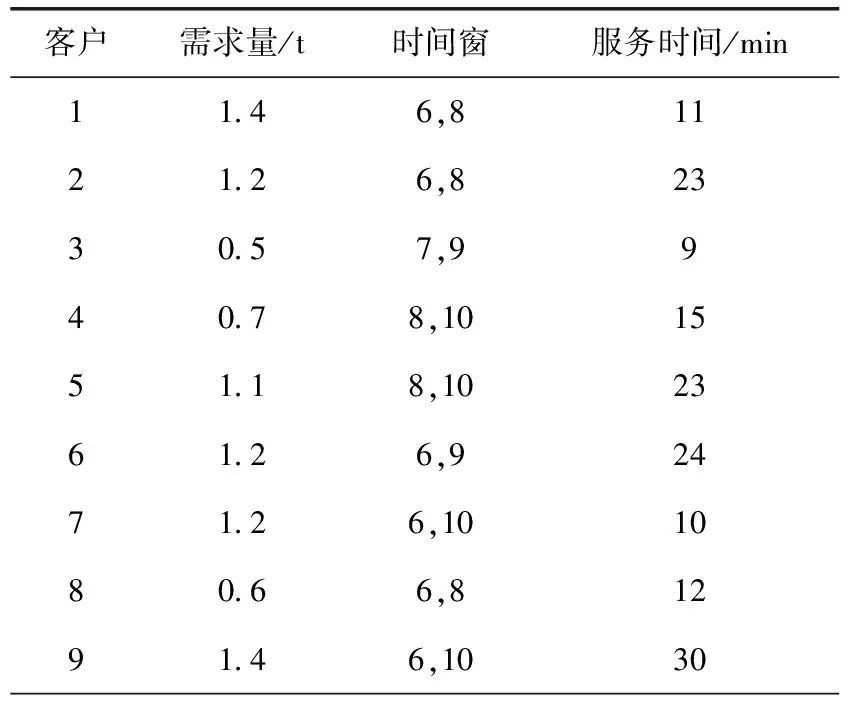


4.2 结果分析



5 结束语
