基于簇内簇间相异度的k-modes算法
2021-09-16贾子琪
贾子琪,宋 玲
(1.南阳理工学院 计算机与软件学院,河南 南阳 473004;2.广西大学 计算机与电子信息学院,广西 南宁 530004)
0 引 言
经典k-means算法[1]在计算簇的均值以及数据对象之间的相异度时使用的是欧式距离,仅适用于连续特征的数值型数据集,对于离散特征的分类型数据集,k-means算法不再适用。Huang对k-means算法[1]进行扩展,使用“modes”代替“means”,提出适用于分类型数据聚类的k-modes算法[2]。k-modes算法采用简单汉明距离计算相异度,忽略了数据对象间同一分类特征的差异性,弱化了簇内相似性,没有充分反映同一分类特征下两个特征值之间的相异度;采用随机选择的方法确定初始簇中心和k值,采用基于频率的方法重新计算和更新簇中心,给聚类结果带来很大的不确定性。
1 相关工作
Ahmad等[3]通过共现分析来反映同一特征下特征值之间的距离,如果特征值之间的共现程度高,则将该特征作为新的簇中心。该方法反映了特征之间的潜在关系,改善了同一特征下特征值相异度系数的计算,但忽略了数据对象本身的异同。Hus等[4]提出了一种基于概念层次的相异度系数。该方法过于依赖用户的经验以及对待聚类数据集专业知识的了解,不利于一般用户的使用,聚类范围有局限性。Ng等[5]扩展了简单汉明距离,考虑当前聚类中modes的影响,基于特征值在簇内出现的频率提出了新的相异度系数。该方法最小化了目标函数,提高了聚类精度,但其相异度系数的计算仍然存在问题。IDMKCA算法只反映了相同特征之间的内在关系,没有考虑不同特征值之间的相似性。如果两个数据对象的特征值不匹配,那么这两个特征值的相异度系数计算结果始终为“1”。Cao等[6]提出基于新相异度系数的IMCDC算法。在新相异度系数下k-modes算法的性能得到了提高,但由于假定数据对象的重要性相同,导致不能充分考虑分类型数据的特点,不能准确地计算数据对象间的相异度。Sangam等[7]在IDMKCA算法基础上提出了基于新的相异度系数的EKACMD算法。该算法在一些情况下确实能够解决IDMKCA算法的部分不足,但是在簇内簇间特征值出现频率相等的情况下,EKACMD算法和IDMKCA算法都存在问题。
2 经典k-modes聚类算法及相关符号说明
2.1 相关符号说明
本文使用的相关符号及含义说明见表1。

表1 符号说明
2.2 k-modes聚类算法
以数据对象xi和簇中心ql为例,定义经典k-modes算法的简单汉明距离,如式(1)所示,此计算赋予各特征相同的权重[8]

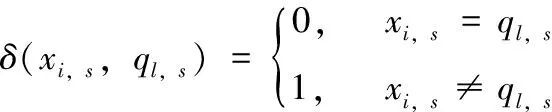
(1)
k-modes算法通过简单汉明距离来最小化的目标函数。如式(2)所示[9]
(2)
3 基于簇内簇间相异度的k-modes算法(IKMCA)
3.1 IKMCA算法的基本思想
如果选用的相异度系数可以发现数据集内全部或部分潜在的modes,那么对基于划分的k-modes算法来说事半功倍。使k-modes算法产生高效的聚类结果需满足簇内数据对象之间的相异度最小;簇间数据对象之间的相异度最大的条件。因此,本节基于簇内簇间相似性提出一种相异度系数“簇内簇间相异度系数”。IKMCA算法使用基于改进的密度峰值算法确定初始簇中心,使用簇内簇间相异度系数计算各数据对象与簇中心之间的相异度,并更新簇中心。
3.2 经典k-modes算法及其变体算法存在的问题
3.2.1 在相异度系数上存在的问题
经典k-modes算法的相异度系数没有考虑簇内特征值出现的相对频率,也没有考虑各特征的簇内簇间结构。导致新数据对象划分过程中,一些簇分配了较少的相似数据。为方便说明,采用表2所示的人工数据集D1对相异度系数进行论证。D1由3个特征描述A={A1,A2,A3}。其中,DOM(A1)={A,B}, DOM(A2)={E,F}, DOM(A3)={H,I}。D1有两个聚类簇C1和C2分别对应的簇中心q1(A,E,H)和q2(A,E,H)。
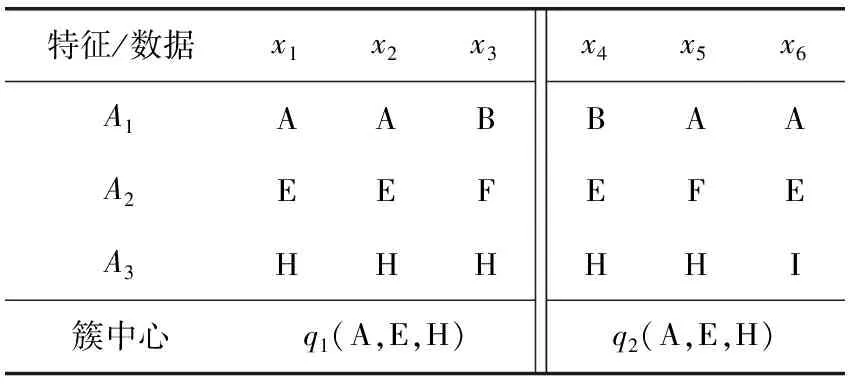
表2 人工数据集D1
假设需要对x7=(A,E,H)进行聚类划分。使用简单满名距离可得d(x7,q1)=d(x7,q2)=0+0+0=0。但以簇内相似性而言,应该将x7划分给簇C1。
3.2.2 在初始簇中心选择上存在的问题
经典k-modes算法对初始簇中心非常敏感,初始簇中心的选择采用随机初始化法或者人工设置法,这两种方法都在一定程度上导致了聚类结果不稳定。选择不同位置和k值的初始簇中心,会产生不同的聚类结果。如图1所示,该数据集的真实簇数是3。选择不同初始簇中心,设置不同的k值,可能产生不同聚类结果,图1内容从左到右依次为:随机选取初始簇中心、聚类迭代过程、最终聚类结果。可见寻找合适的初始簇中心非常重要。
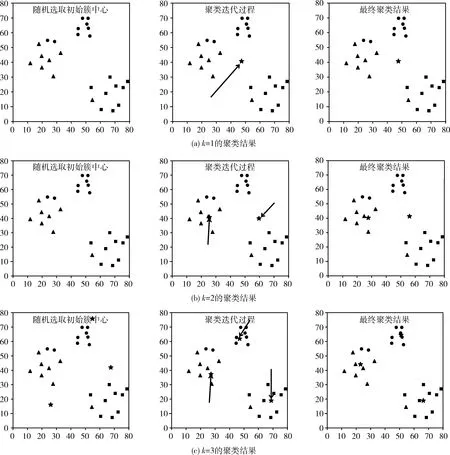
图1 k-modes算法对初始簇中心选取的敏感性
3.3 考虑簇内相似性的相异度系数
簇内簇间相异度系数考虑特征值在同一簇内分布的相对频率。属于同簇的数据对象,其相同的特征值出现的频率较高,簇内相似性也较高。簇内相异度定义如式(3)所示[10]
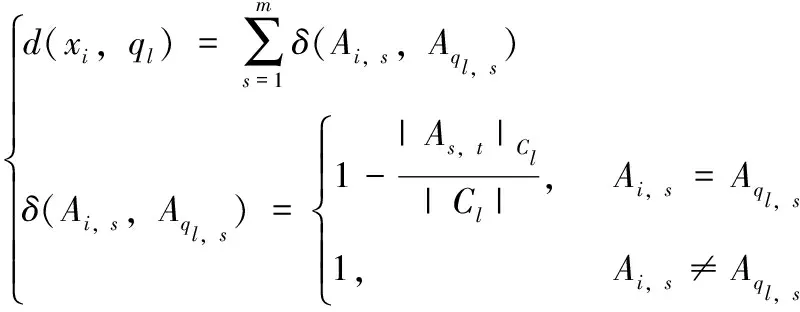
1≤i≤n, 1≤s≤m
(3)
使用数据集D1,根据式(3)可得d(x10,q1)=(1-2/3)+(1-2/3)+(1-1)=2/3,d(x10,q2)=(1-2/3)+(1-2/3)+(1-2/3)=1。由计算结果可知,x7与簇C1具有最小相异度,因此x7应该被划分到簇C1内。式(3)虽然考虑了簇内特征值的相对频率,但没有考虑簇间特征值的分布。使用表3所示人工数据集D2讨论不考虑簇间相似度的缺陷。D2由3个分类型特征描述A={A1,A2,A3}。
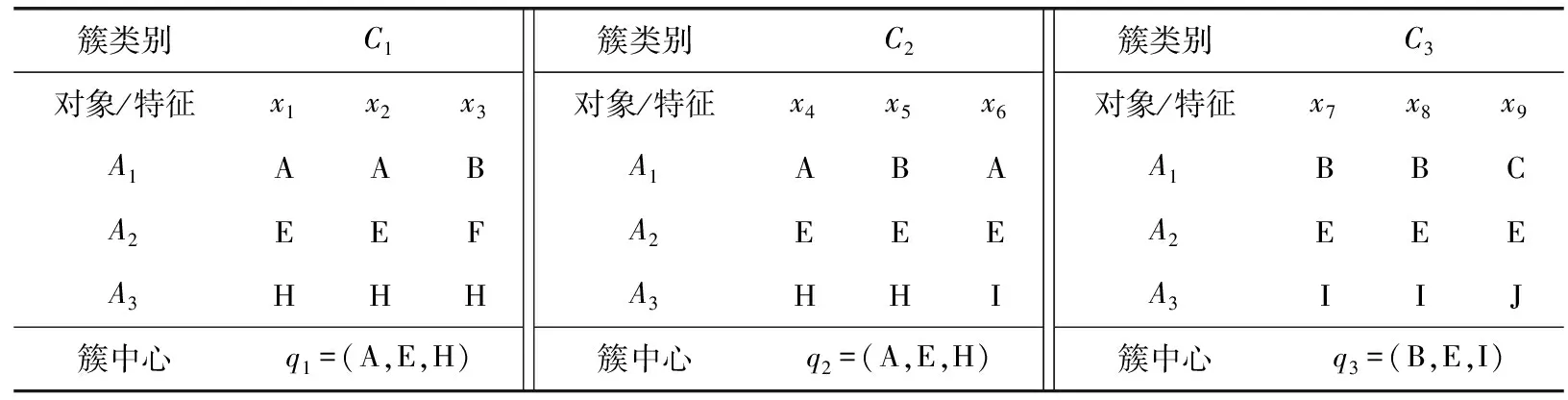
表3 人工数据集D2
其中,DOM=(A1)={A,B,C}, DOM(A2)={E,F},DOM(A3)={H,I,J}。D2有3个聚类簇C1,C2和C3分别对应簇中心q1=(A,E,H),q2=(A,E,H)和q3=(B,E,I)。
假设需要对x10=(A,E,H)进行聚类划分。使用简单汉明距离可得d(x10,q1)=d(x10,q2)=d(x10,q3)=0+0+0=0。使用式(3)可得d(x10,q1)=(1-2/3)+(1-2/3)+(1-3/3)=2/3,d(x10,q2)=(1-2/3)+(1-3/3)+(1-2/3)=2/3,d(x10,q3)=1+0+1=2。由上述计算结果可知,简单汉明距离不能对x10进行聚类划分;式(3)可以将x10划分给簇C1或簇C2,即式(3)无法准确地确定x10的正确聚类划分。从“低簇内相异度高簇间相异度”角度观察数据集D2,可知将x10分配给簇C1更合适。因为将x10分配给簇C1后,会让簇C1和簇C2之间的相异度最大化。
3.4 考虑簇内簇间相似性的相异度系数
簇间相异度考虑特征值相对于所有簇分布的总频率。假设特征值仅在一个簇内频繁分布,意味该特征值和其它簇之间的差异性很大。簇内簇间相异度系数定义如式(4)所示[11]
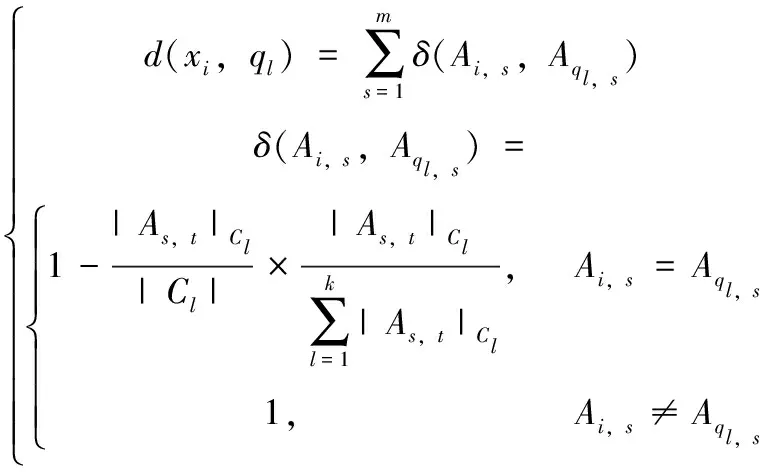
1≤i≤n, 1≤s≤m
(4)
使用式(4)数据集D2进行计算d(x10,q1)=(1-2/3×2/4)+(1-2/3×2/8)+(1-3/3×3/5)=1.9;d(x10,q2)=(1-2/3×2/4)+(1-3/3×3/8)+(1-2/3×2/5)=2.025;d(x10,q3)=(1-0×1)+(1-3/3×3/8)+(1-0×1)=2.625。根据式(4)的计算结果可知,x10与簇C1之间的相异度更小,这个结果与之前的分析一致,成功的对x10进行了聚类划分。下面使用式(4)验证更为特殊的人工数据集D3。如表4所示,D3由3个特征描述A={A1,A2,A3}。其中,DOM=(A1)={A,B},DOM(A2)={E,F},DOM(A3)={H,I},3个聚类簇C1,C2和C3分别对应簇中心q1=(A,E,H),q2=(A,E,H)和q3=(A,E,H),A,E和H在D3中均匀分布,均出现6次。

表4 人工数据集D3
分别使用简单汉明距离、式(3)和式(4)对x10(A,E,H)进行聚类划分。使用简单汉明距离可得d(x10,q1)=d(x10,q2)=d(x10,q3)=0+0+0=0;使用式(3)可得d(x10,q1)=d(x10,q2)=d(x10,q3)=(1-2/3)+(1-2/3)+(1-2/3)=1;使用式(4)可得d(x10,q1)=d(x10,q2)=d(x10,q3)=(1-2/3×2/6)+(1-2/3×2/6)+(1-2/3×2/6)=21/9。由上述计算结果可知,当特征值均匀分布时,上述3种相异度系数都无法正确对x10进行聚类划分。因此再一次考虑完善簇内簇间相异度系数。
3.5 完善的簇内簇间相异度系数
取数据对象xi的特征值分布与所在簇的整体特征值分布进行比较,完善算子ζl的定义如式(5)所示
(5)
xi是待划分数据对象,xj是簇Cl内的数据对象。重新定义的簇内簇间相异度系数如式(6)所示
(6)
对任意xi,xj∈D,d均有以下性质:
自身距离:对所有xi,每个对象与自身的距离等于零d(xi,xi)=0。
对称性:对所有xi和xj,xi到xj的距离等于xj到xi的距离,即d(xi,xj)=d(xj,xi)。
非负性:对所有xi和xj,距离d是个非负值,当且仅当xi=xj时,d(xi,xj)=0。
满足三角不等式:对所有xi和xj,存在d(xi,xj)≤d(xi,xh)+d(xh,xj)。

3.6 分类型数据初始化方法
2014年,Rodriguez等提出密度峰值(DP)算法[12]。DP算法是一种基于相对距离和局部邻域密度的新型聚类算法,处理的是数值型数据,其输入是数据对象间的相异度矩阵,因此通过合适的相异度系数计算出分类型数据之间的相异度,就可将DP算法应用到分类型数据聚类上。本节利用DP算法可以自动确定聚类簇数的优点去确定初始簇中心。
3.6.1 数据对象xi的局部邻域密度ρi
局部邻域密度ρi的值等价于以数据对象xi为圆心,以截断距离dc为半径区域内的数据对象个数。xi的局部邻域密度有方波内核函数法和高斯核函数法两种定义方法。方波内核函数法适用于大规模数据集,高斯核函数法适用于小规模数据集。方波内核函数法求ρi的定义如式(7)所示
(7)
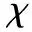
K(x)=exp{-x2}
(8)
从式(7)和式(8)可知,dc的取值会直接影响ρi的大小,进而影响簇中心的选择和整个聚类结果。因此,确定合适的dc值对算法来说很重要。
3.6.2 数据对象xi和xj之间的相对距离Li
xi和xj之间的相对距离Li的定义如式(9)所示
(9)
当xi的ρi不是最大密度时,Li定义为在所有局部邻域密度比xi大的数据对象中,与xi距离最近的数据对象与xi之间的距离,如式(10)和图2所示
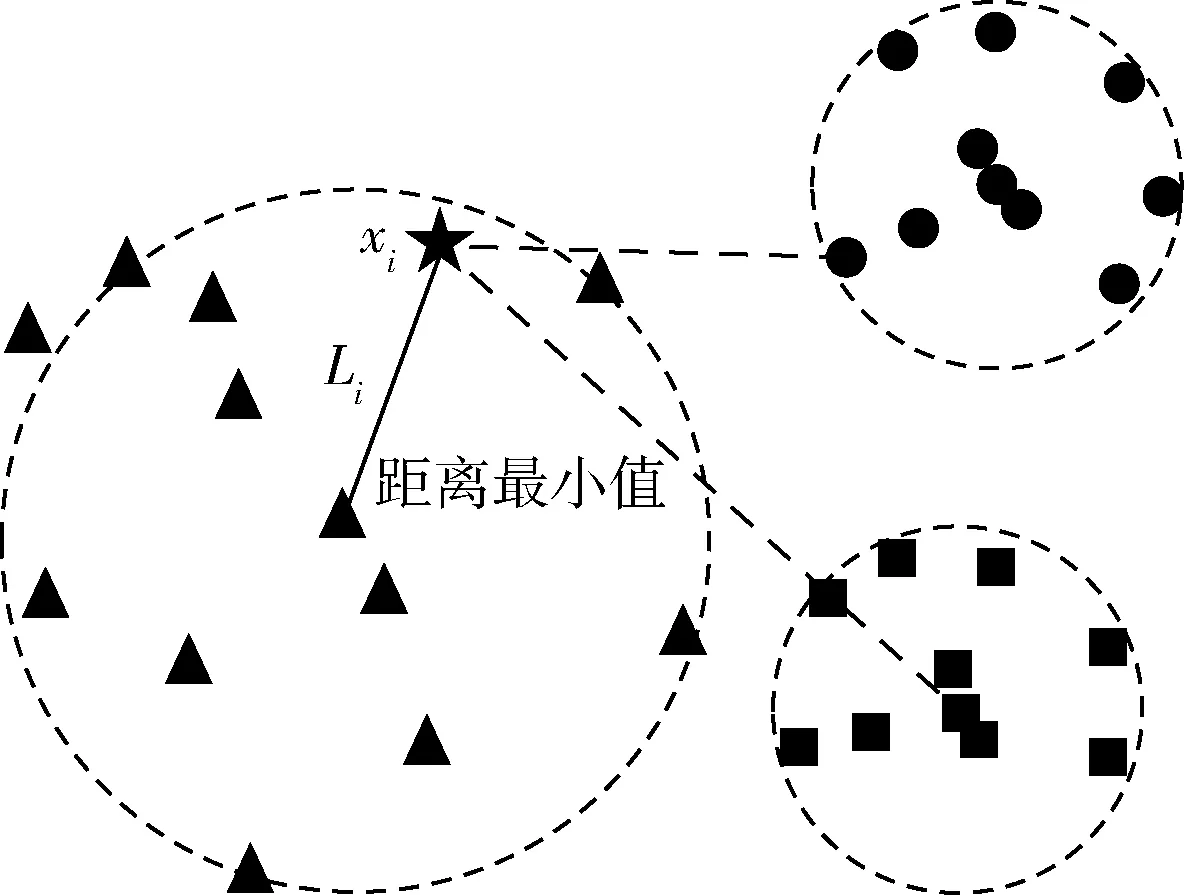
图2 xi的局部邻域密度不是最大密度时的情况
(10)
当xi的ρi是最大密度时,Li定义为在所有局部邻域密度比xi大的数据对象中,距xi最远的数据对象与xi之间的距离,如式(11)和图3所示。同时具备高Li和高ρi的数据对象即为簇中心
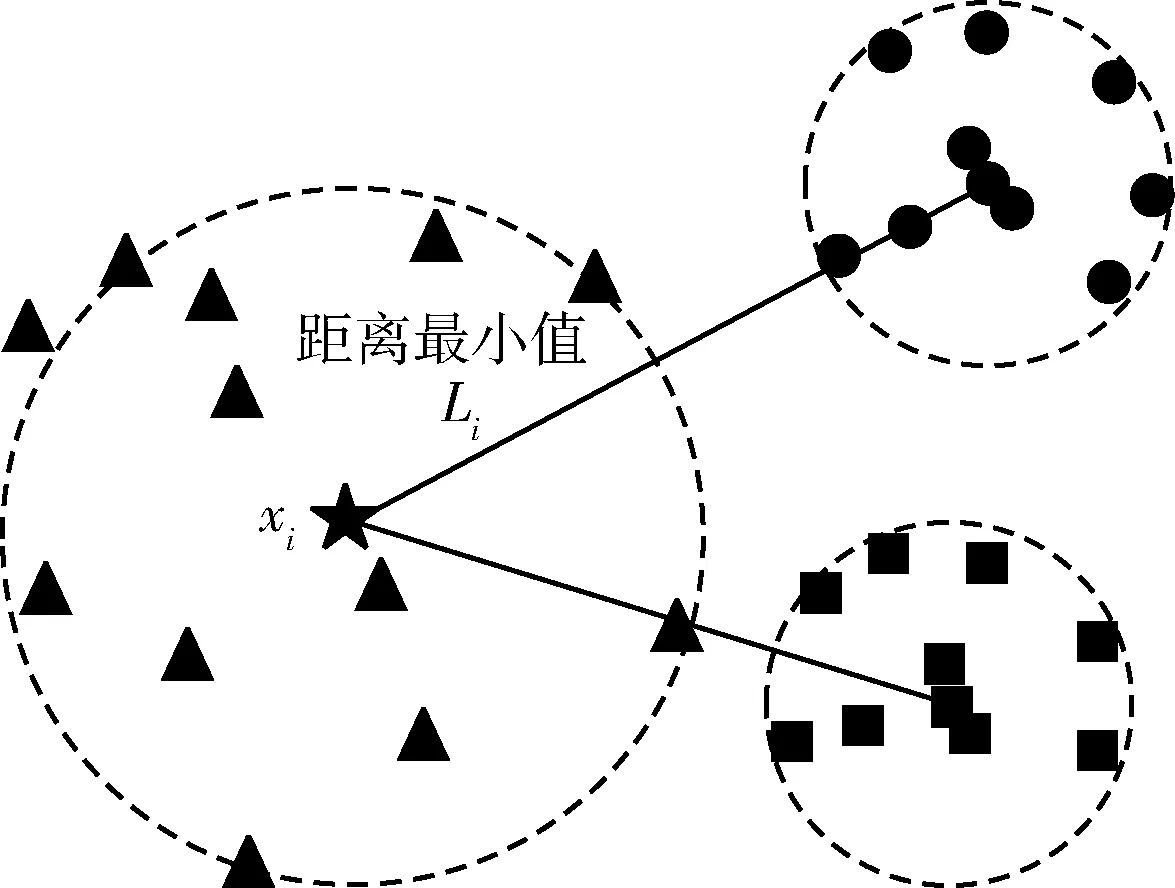
图3 xi的局部邻域密度是最大密度时的情况
(11)
3.6.3 截断距离
截断距离dc是一个限定距离搜索范围的临界值。DP算法的dc值需要人为确定,将数据集中两两数据对象间的距离升序排列,取前1%至2%位置处的值即为dc值,是一个大概范围。在实际聚类问题中dc值设置过大,会导致求得的ρi重叠,dc值设置过小,会导致聚类簇分布稀疏。受文献[13]启发本节给出详细的dc值确定方法。设定di,j=[di,1,di,2,…,di,n]为数据对象xi与xj的相异度。用式(1)计算di,j值,然后对di,j升序排序得到d′i,j=[d′i,1,d′i,2,…,d′i,n]。xi的截断距离dc,i定义如式(12)所示
(12)
max(d′i,j+1-d′i,j)是d′i,j中相邻相异度的最大差值,设定d′i,j=da,d′i,j+1=db。如图4所示,数据对象xi与和它同簇的数据对象相异度较小,与和它不同簇的数据对象相异度较大。因此,在d′i,j=[d′i,1,d′i,2,…,d′i,j,d′i,j+1,…,d′i,n]内一定存在一个临界位置使得d′i,j+1与d′i,j的差值最大,认为数据对象xi和数据对象a属于同一簇,与数据对象b属于不同簇。数据对象xi的dc,i值定义如式(13)所示
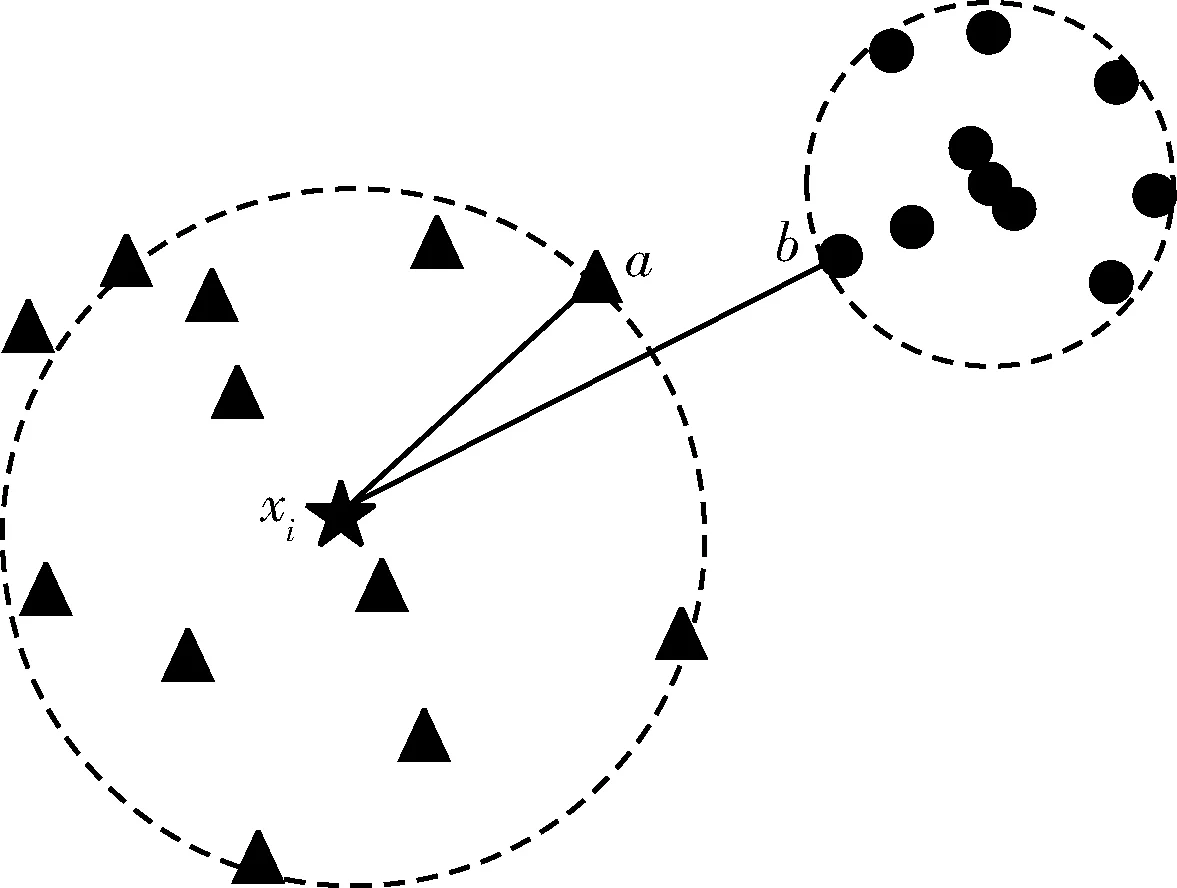
图4 dc,i值的确定
(13)
dc值定义为集合dc,i的最小值如式(14)所示
dc=min(dc,i)
(14)
3.6.4 簇中心的确定
IKMCA基于以下两个假设确定初始簇中心:①簇中心的局部邻域密度高于周围非簇中心点;②各簇中心之间的相对距离较大。基于上述假设,本节给出初始簇中心自动确定的方法。如图5所示是一个二维示例数据集,共有93个数据对象,2个聚类簇,对应2个簇中心。

图5 二维数据集
DP算法簇中心的选择是通过决策图确定的。如图6所示决策图的横轴为数据对象xi的局部邻域密度ρi,纵轴为相对距离Li。ρi和Li的值同时大的值即为数据集的簇中心。图6右上角的两个点即为图6中两个簇对应的簇中心。簇中心周围包围着大量的数据对象,其局部邻域密度ρi和相对距离Li都较大。
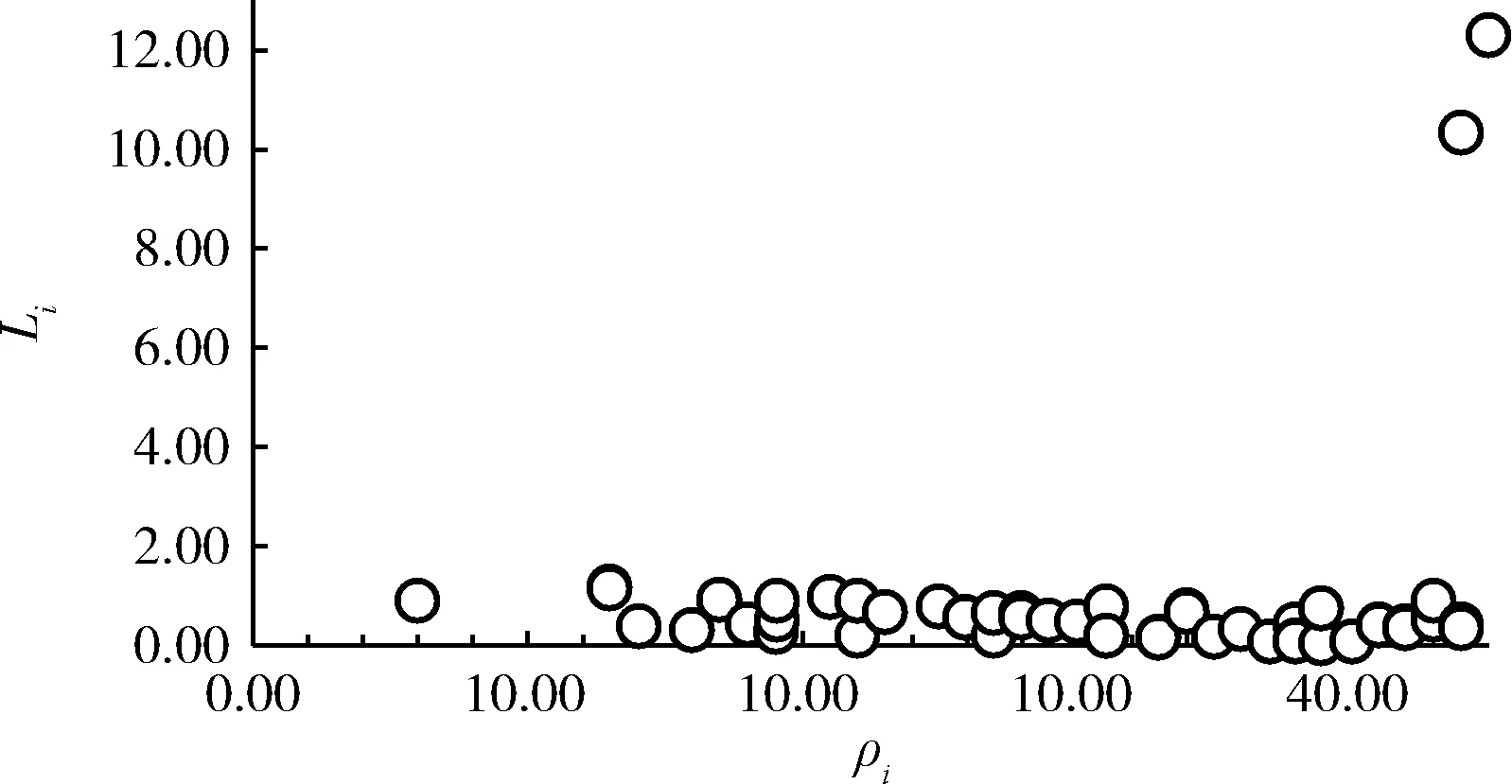
图6 决策图
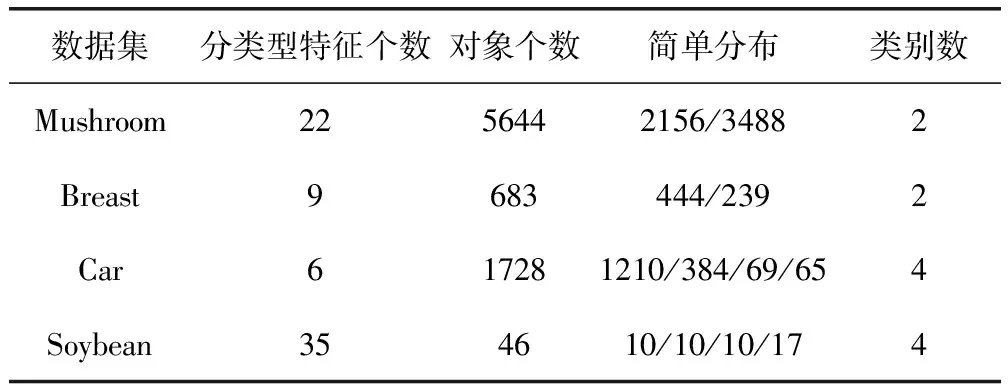
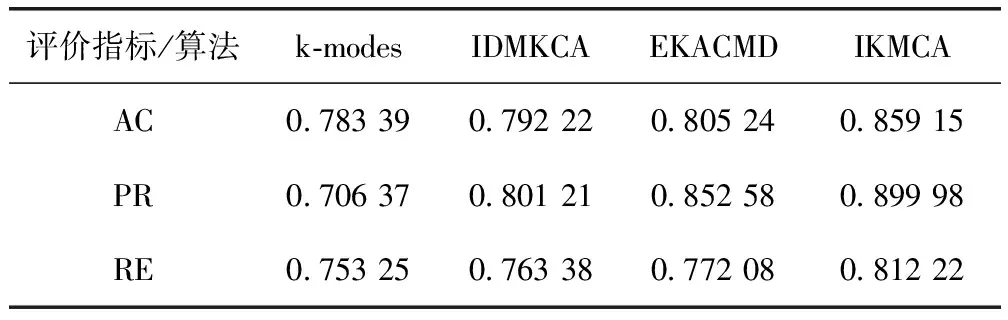
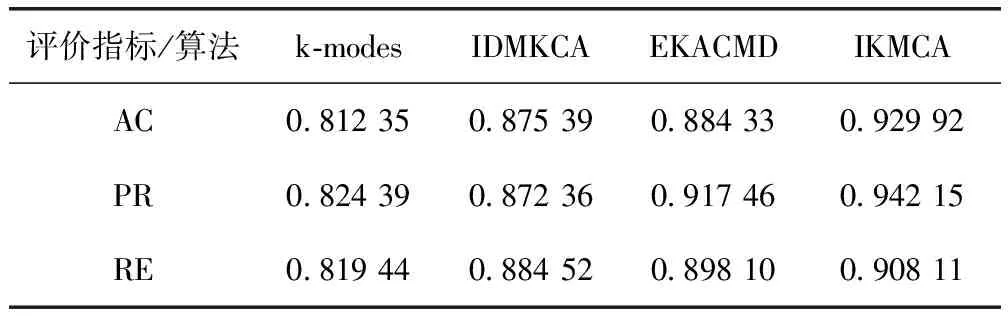
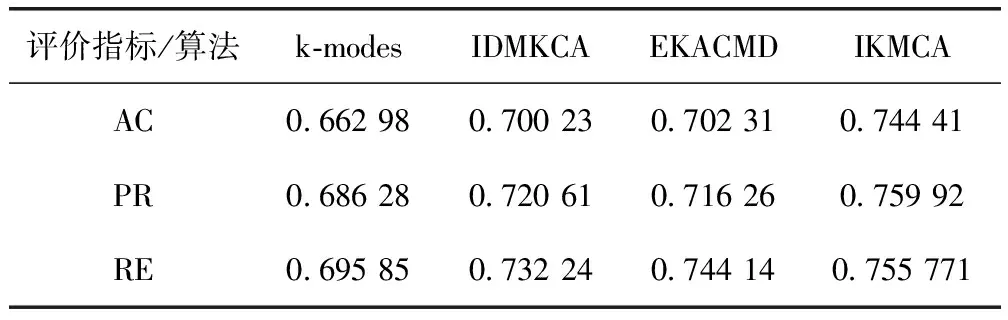
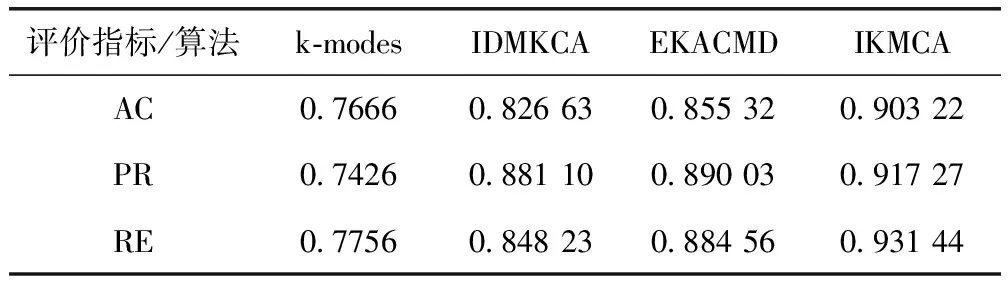
为了更加直观观察和确定簇中心,考虑使用Zi决策图来选择簇中心。通过式(8)和式(9)得到每个数据对象的局部邻域密度和相对距离。根据公式Zi=ρi×Li计算出所有数据对象的Zi值,将Zi值降序排序得到排序序列Z(1)>Z(2)>…Z(n),其中Z(1)>Z(2)>…Z(k),(k 图7 Zi决策图 新的簇内簇间相异度系数使分类型数据相异度计算更加准确。初始簇中心的自主选取避免了经典k-modes算法随机选取或者人为手动设置带来的聚类结果不确定。DP算法只给出dc的大致范围,本文在DP算法的基础上给出了dc的明确确定方法。将簇内簇间相异度系数应用到经典k-modes 算法中,其目标函数定义如式(15)所示。定理1展示了如何最小化目标函数F(U,Q) (15) uil∈{0,1}, 1≤i≤n, 1≤l≤k (16) (17) (18) Un×k是满足约束条件(16)~(18)的隶属度矩阵,uil=1表示xi属于簇Cl。在满足约束条件(16)~(18)的情况下,目标函数F(U,Q)达到极小值,此时可以判断聚类算法结束。 定理1 IKMCA的簇中心选取应使得函数F(U,Q)被最小化,当且仅当fs,ts(xi)≥fs,th(xi),ts≠th(1≤s≤m)。文字描述为,簇中心的各特征值应选取数据集中各特征上出现频率最大的特征值。fs,t(xi)(1≤s≤m, 1≤t≤ns)表示xi在第s个特征下取值为As,t的个数,如式(19)所示 fs,t(xi)=|{xi∈D,xi,s=As,t}| (19) 当且仅当ql=DOM(As), 1≤s≤m并且满足式(20) fs,ts(xi)≥fs,th(xi),且ts≠th(1≤s≤m) (20) 时,函数F(U,Q)被最小化。为了使目标函数F(U,Q)达到极小值,改进后的算法步骤描述如下: 基于簇内簇间相异度的k-modes算法(IKMCA) 输入:包含有n个对象,m个分类型特征的分类型数据集D; (1)通过式(1)计算相异度di,j,并得到相异矩阵dn×n; (2)根据式(14)计算截断距离dc; (3)利用式(7)或式(8)计算局部邻域密度ρi; (4)利用式(9)计算相对距离Li; (5)根据公式Zi=ρi×Li,计算得到Zi={Z1,Z2,…,Zn}; (6)将Zi降序排序,得到排序序列Z(1)>Z(2)>…>Z(n)。以数据对象xi的下标为横坐标,以Zi为纵坐标绘制Zi决策图,确定图中的拐点,拐点处的值即为最佳k值。 (7)确定k值和初始簇中心集合q(0)={q1,q2,…,qk}; (8)根据式(6)计算数据集中n-k个数据对象与k个簇中心之间的相异度d(xi,ql); (9)根据就近原则将数据对象分配到离它最近的初始簇中去,分配完成后,得到k个聚类簇C(1)={C1,C2,…,Ck},标记这(n-k)个数据对象的簇标签; (10)在新形成的聚类簇上根据定理1更新簇中心q(1)={q1,q2,…,qk}; (11)重复上述步骤(8)~步骤(10),直到目标函数不再发生变化。如果不再发生变化,则算法结束;否则,跳至步骤(8)继续执行。 (12)算法结束,完成聚类。 输出:聚类完成的簇集合C={C1,C2,…,Ck}; IKMCA流程如图8所示。 图8 IKMCA流程 假设l是算法收敛所需的迭代次数,通常情况下n>>m,k,l。IKMAC算法的时间复杂度主要是在每次迭代中更新簇中心和相异度。初始化簇中心需要人工观察决策图决定,因此此阶段的时间复杂度暂不考虑进总体算法中。使用簇内簇间相异度在每次迭代中更新簇中心和相异度计算的时间复杂度是l(O(nmk)+O(nmk))=O(nmkl),所以IKMCA的总时间复杂度是O(nmkl)。从上述分析可以发现,使簇内簇间相异度的IKMCA算法的时间复杂度相对数据对象的数量、聚类个数和特征个数是线性可缩放的。 3.8.1 性能指标 为评估提出算法的有效性,下面分别从聚类精度AC[14]、纯度PR[15]、召回率RE[2]这3个指标对聚类结果进行评价,分别如式(21)~式(23)所示。NUM+表示被正确划分到簇Cl的数据对象个数;NUM-表示没有被正确划分到簇Cl的数据对象个数;NUM*表示应该被划分到簇Cl但实际上没有被划分到簇Cl的数据对象个数。聚类结果与数据集的真实划分越接近,AC、PE和RE的值就越大,算法越有效 (21) (22) (23) 3.8.2 实验环境及数据集描述 算法用Python语言实现,所有实验均在intel(R)Core(TM)处理器i7-8700K CPU@3.70 GHz,Windows 10操作系统上运行。使用数据集来自真实数据集。UCI[16]是加州大学欧文分校提供的专门用于机器学习的真实数据集。为了测试算法的有效性,从UCI数据集中选取Mushroom(简称Mus),Breast-cancer(简称Bre),Car和Soybean-small(简称Soy)数据集进行实验验证。表5列出了这些数据集详细信息。 表5 数据集描述 3.8.3 实验结果分析 将本文提出的IKMCA算法与Huang提出的k-modes算法、Ng等提出IDMKCA算法和Ravi等提出EKACMD算法分别运行30次取平均值。AC、PE和RE的计算结果见表6~表9。 表6 4种算法在Mus数据集下的实验结果 表7 4种算法在Bre数据集下的实验结果 表8 4种算法在Car数据集下的实验结果 表9 4种算法在Soy数据集下的实验结果 从上述实验结果可以看出,对于Mus、Bre、Car和Soy数据集而言,大多数情况下IKMCA在AC、PR和RE上优于k-modes算法、IDMKCA算法和EKACMD算法。IMKCA算法优于经典k-modes算法的原因是,k-modes算法的预处理破坏了分类型特征的原始结构。转换后的分类特征值使用简单汉明距离计算相异度系数并不能揭示分类型数据之间的相异度。当数据集的特征非常多时,简单的0-1对比可能产生非常大的相异度,也可能产生非常小的相异度甚至是相异差异度。跟经典k-modes算法和IDMKCA、EKACMD算法相比,提出的簇内簇间相异度可以更好地揭示数据集的结构。 经典k-modes算法使用简单汉明距离进行相异度计算,弱化了类内相似性,忽略了簇间相似性。针对这些问题,本文基于簇内簇间相似性提出相异度计算方法。该方法可以防止聚类过程中的重要特征值的丢失,强化了簇内特征值之间的相似性,弱化了簇间特征值之间的相似性。提出的簇中心自动选择方法大大减少了随机选取簇中心或者手动选择选取簇中心给聚类带来的误差。本文用一些说明性例子讨论了k-modes算法中使用简单汉明距离等其它几种相异度系数的局限性,并提出了一种相异度系数。基于本文提出相异度系数改进的分类型数据聚类算法与基于其它相异度系数的k-modes算法在UCI数据集上进行了实验。实验结果表明,本文提出的相异度系数计算方法保留了数据的特征,做到了低簇内相异度高簇间相异性的标准,在聚类精度、纯度和召回率方面均有提高,有效提高了分类型数据的聚类效果。
3.7 IKMCA描述
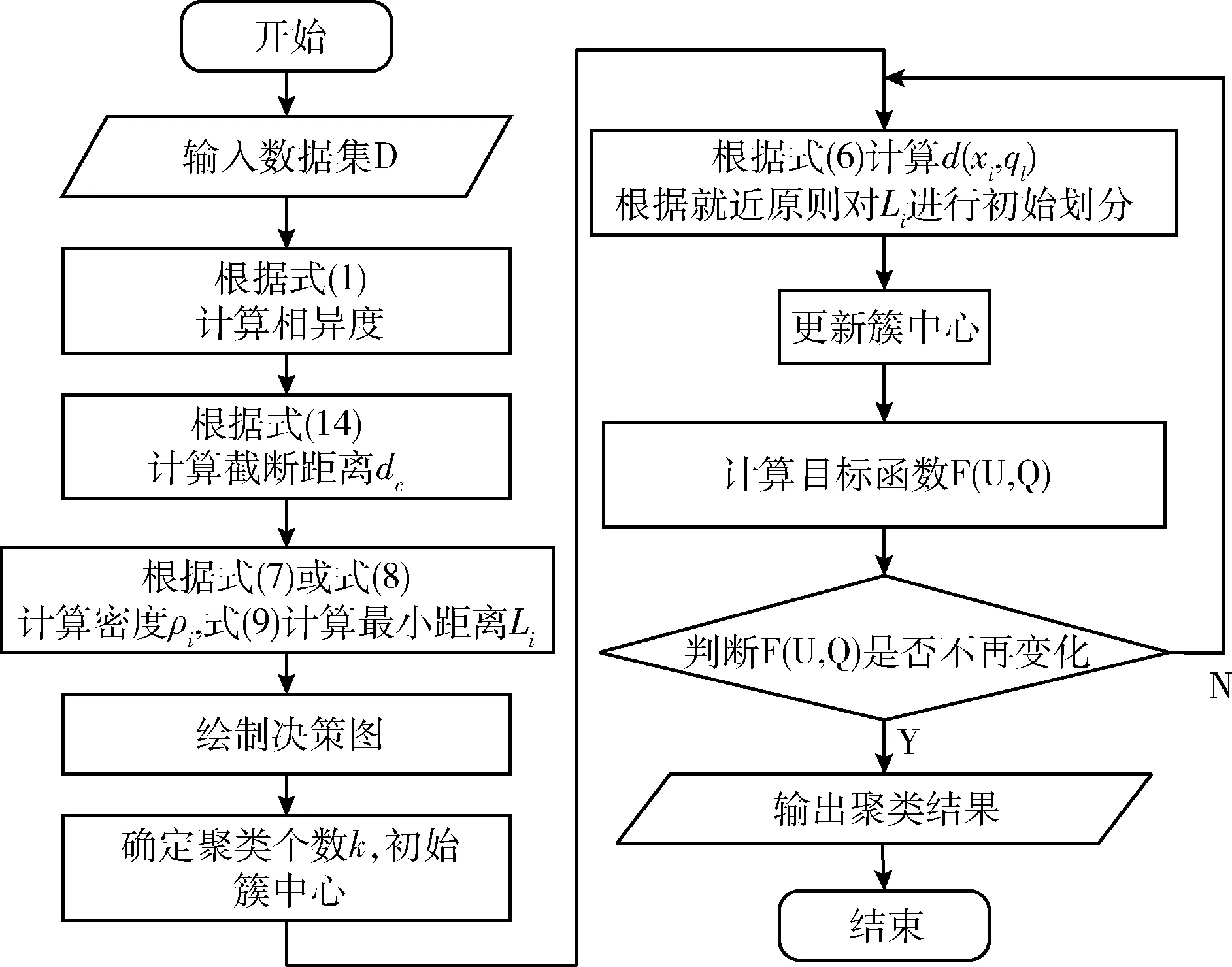
3.8 实验及结果分析
4 结束语
