一种新的改进Apriori算法*
2010-05-18杨金凤
杨金凤,刘 锋
(安徽大学 计算机科学与技术学院,安徽 合肥 230039)
数据挖掘DM(Data Mining)出现于 20世纪80年代后期,是在数据库技术的基础上,结合人工智能、机器学习、统计学、神经网络等多种学科技术产生的具有很强生命力的新研究领域。其中关联规则挖掘研究[1-2]是一项重要的内容,目的是发现大规模数据集中项集之间有趣的关联关系或模式。
频繁项集的挖掘是关联规则挖掘的核心,如何高效地从海量数据库中找出频繁出现的项集是世界范围内的热门研究课题。
1 相关概念[1]
设 I={I1,I2,…,Im}是项的集合,称为项集,包含 k 个项的项集称为k项集。D是数据库事务的集合,数据库中的每个事务T是项的集合,T⊆I,TID是事务 T的标识符。设A是一个项集,事务T包含A,当且仅当A⊆T,一个包含k个项的事务T可以产生2k个非空的子项集。
规则A⇒B的支持度s是D中同时包含A和B的事务占总事务的百分比。规则A⇒B的支持度c是D中同时包含A和B的事务占包含A的事务的百分比。项集的出现频率是包含项集的事务数,称为项集的支持度计数。项集的支持度计数除以总的事务数就是相对支持度计数,如果项集I的相对支持度计数不小于预定义的最小支持度阈值,则称此项集是频繁项集,否则是不频繁项集。
2 Apriori算法和优化
2.1 经典的Apriori算法[2-6]
Apriori是一种逐层搜索的迭代方法,即用k项频繁项集探索(k+1)项频繁项集。首先,扫描数据库找出频繁1项集的集合,该集合为L1。用L1找频繁2项集的集合L2,用L2找 L3,如此下去直到不能再找到频繁项集。找每个Lk需要1次数据库全扫描。
为了提高频繁项集逐层产生的效率,一种称作Apriori的重要性质用于压缩搜索空间。Apriori性质为频繁项集的所有非空子集也必须是频繁的。
Apriori算法是由连接步和剪枝步组成。(1)连接步:为找Lk,通过将Lk-1与自身连接产生候选k项集的集合。该候选项集合为 Ck。(2)剪枝步:Ck是 Lk的超集,即Ck的成员可能是频繁的;也可能是不频繁的。扫描数据库确定Ck中每个候选项集的计数,从而确定Lk(即根据定义,计数值不小于最小支持度计数的所有候选项集是频繁的,从而属于Lk)。然而Ck可能很大,因此所涉及的计算量就很大。为压缩Ck,可以使用Apriori性质。任何非频繁的(k-1)项集都不是频繁k项集的子集。因此,如果候选 k项集的(k-1)项子集不在Lk-1中,则该候选项集也不可能是频繁的,从而可以从Ck中删除。
经典的Apriori算法在产生候选项集上,由Lk-1自连接产生Ck,然后再利用Apriori性质对Ck进行删减。设l1和 l2是 Lk-1中的项集。 记号 li[j]表示 li中的第 j项(例如,l1[k-2]表示l1的倒数第 2项)。Apriori假定事务或项集中的项按字典次序排序。执行Lk-1的自连接,如果它们的前(k-2)个项相同的话,则可以连接。例如,(l1[1]=l2[1])∧(l1[2]=l2[2])∧… ∧(l1[k-2]=l2[k-2])∧(l1[k-1]<l2[k-1]),那么 l1和 l2是可以连接的,否则是不可以连接的,连接结果项集是 l1[1],l1[2],…,l1[k-1],l2[k-2]。 然后再利用 Apriori性质进行判断项集 l1[1],l1[2],…,l1[k-1],l2[k-2]是否可能是频繁的,这样需要先产生项集l1[1],l1[2], … ,l1[k-1],l2[k-2]的(k-1)个 (k-1)项子集 ,然后依次比较(k-1)个子集是否在Lk-1中,如果出现不在,则删减项集 l1[1],l1[2], … ,l1[k-1],l2[k-2]; 如果都在,再对数据库扫描,进行计数。
2.2 对Apriori算法的改进
通过上面的分析发现,为了生成Ck,在连接步骤需要大量的比较,而且由连接产生的项集即使后来由Apriori性质确定了它不是候选项集,但在确定之前仍然需要对它生成子项集,并对子项集进行确定是否都在Lk-1中。这些步骤浪费了大量的时间,如果可以保证由连接步生成的项集都是候选项集的话,那么可以省掉不必要的连接比较和剪枝步骤。下面介绍改进后的算法。
首先对Lk-1中的每项进行扫描,记下项集{l1[1]},{l1[1],l1[2]},…,{l1[1],l1[2],…,l1[k-2]},{l2[1]},{l2[1],l2[2]},…,{l2[1],l2[2],…,l2[k-2]},{l3[1]},…。 设 1 个 k项集 li={li[1],li[2], … ,li[k-1],li[k]}, 由 Apriori 性质知道,如果 li属于 Ck,那么以下的(k-1)个(k-1)项集就必须都出现在 Lk-1中,所以{li[1]}至少要出现(k-2)次,{li[1],li[2]}至少要出现 (k-3)次 , 依次类推 {li[1],li[2],…,li[k-1]}至少要出现 1次。设扫描得到的{li[1]}出现次数为 a,如果 a<(k-2),则可以将 Lk-1中所有以 li[1]开头的(k-1)项集全部删除,如果a≥(k-2),那么比较扫描得到的{li[1],li[2]}出现次数 b 与(k-3)的大小,若 b<(k-3),则删除 Lk-1中所有以{li[1],li[2]}开头的项集,如果b≥(k-3),则继续比较下一项。通过简单的数字比较,可以大量地从Lk-1中删除项集,这样可以大大地减少不必要的连接。连接生成的k项集,也只需要比较1次就可以确定是否属于Ck,其算法如下:
输入:D(事物数据库);
min_sup:最小支持度计数阈值。
输出:L(D中的频繁项集)。
(1)扫描数据库D,生成频繁1项集L1;
(2)由频繁1项集生成频繁2项集L2;
(3)for(i=1;li∈Lk;i++)。
(4)累加{li[1]}、{li[1],li[2]}、…、{li[1],li[2], …,li[k-1]}的出现次数;
(5)将只含 li[1]项的项集出现次数 a与(k-1)比较大小,如果a小于(k-1),则删除 Lk中的所有以 li[1]项开头的项集,从li+1[1]项的项集出现次数开始比较;如果a大于(k-1),再比较以{li[1],li[2]}开头的项集出现次数 b与(k-2)的大小。如果 b小于(k-2),则删除 Lk中的所有以{li[1],li[2]}开头的项集,并将只含 li[1]项的项集出现次数赋值为(a-b),再对(a-b)与(k-1)进行比较;如果 b大于(k-2),再对以{li[1],li[2],li[3]}开头的项集出现次数c与(k-3)的大小进行比较。依次类推,删除后Lk项集为 Lk′。
(6)用 Lk′中的项集自连接生成 C′k+1;
(7)for(i=1;li∈C′k+1;i++)
if({li[2],li[3],…,li[k]}∈Lk)
li是候选项集,放入 Ck+1中;
(8)扫描数据库,对Ck+1中项集进行计数,如果大于min_sup,就是频繁项集,放入Lk+1中。
3 实例说明
通过由频繁3项集生成4项候选集的例子,说明是如何通过改进的算法在连接前对频繁3项集进行删减的。 设 L3={{I1,I2,I3},{I1,I2,I6},{I2,I3,I4},{I2,I3,I5},{I2,I4,I5},{I3,I4,I5},{I3,I5,I6},{I4,I5,I6}}。 扫描 L3,得到相关的计数。表1所示为删减L3中项集的过程。
经过删减得 Lk′={{I2,I3,I4},{I2,I3,I5}},Lk′自连接只生成 1 个 4 项集{I2,I3,I4,I5}。 {I3,I4,I5}∈L3,所以 ,得到候选项集 C4={I2,I3,I4,I5}。 通过验证,结果是正确的。
如果采用经典的Apriori算法,先连接生成2个4项集{I1,I2,I3,I6},{I2,I3,I4,I5}, 再进行剪枝 , 最坏情况下 ,需要扫描8个子项集是否在L3中,才能确定,{I1,I2,I3,I6},{I2,I3,I4,I5}是否为候选项集 , 最好的情况下也需要扫描2个子集。而采用新的算法,只连接生成1个4项集,再进行剪枝步,只需要扫描 1个子项集{I3,I4,I5}是否在 L3中。
本文运用新的算法,从另一个先删减再连接的新视角来生成频繁项集,可以减少大量的无用连接,进而也减少了剪枝步需要判断是否为候选项集的数量,在时间上提高了效率。但是对Apriori算法改进的并不彻底,依然需要大量的数据库扫描,在未来的研究工作中着力解决多次扫描数据库的问题。
[1]HAN Jia Wei,KAMBER M.数据挖掘概念与技术[M].范明,孟小峰,译.北京:机械工业出版社,2007.
[2]杨明,孙志挥,宋余庆.快速更新全局频繁项目集 [J].软件学报 ,2004,15(8):1189-1196.
[3]郭健美,宋顺林,李世松.基于 Apriori算法的改进算法 [J].计算机工程与设计,2008,29(11):2814-2815.
[4]冯兴杰,周谆.Apriori算法的改进[J].计算机工程,2005,31(21):172-173.
[5]朱其祥,徐勇,张林.基于改进 Apriori算法的关联规则挖掘研究[J].计算机技术与发展,2006,16(7):102-104.
[6]MING Cheng Tseng, WEN Yang Lin, RONG Jeng.Dynamic mining of multi-supported association rules with classification ontology[J].网际网路技术学刊, 2006,7(14):399-406.
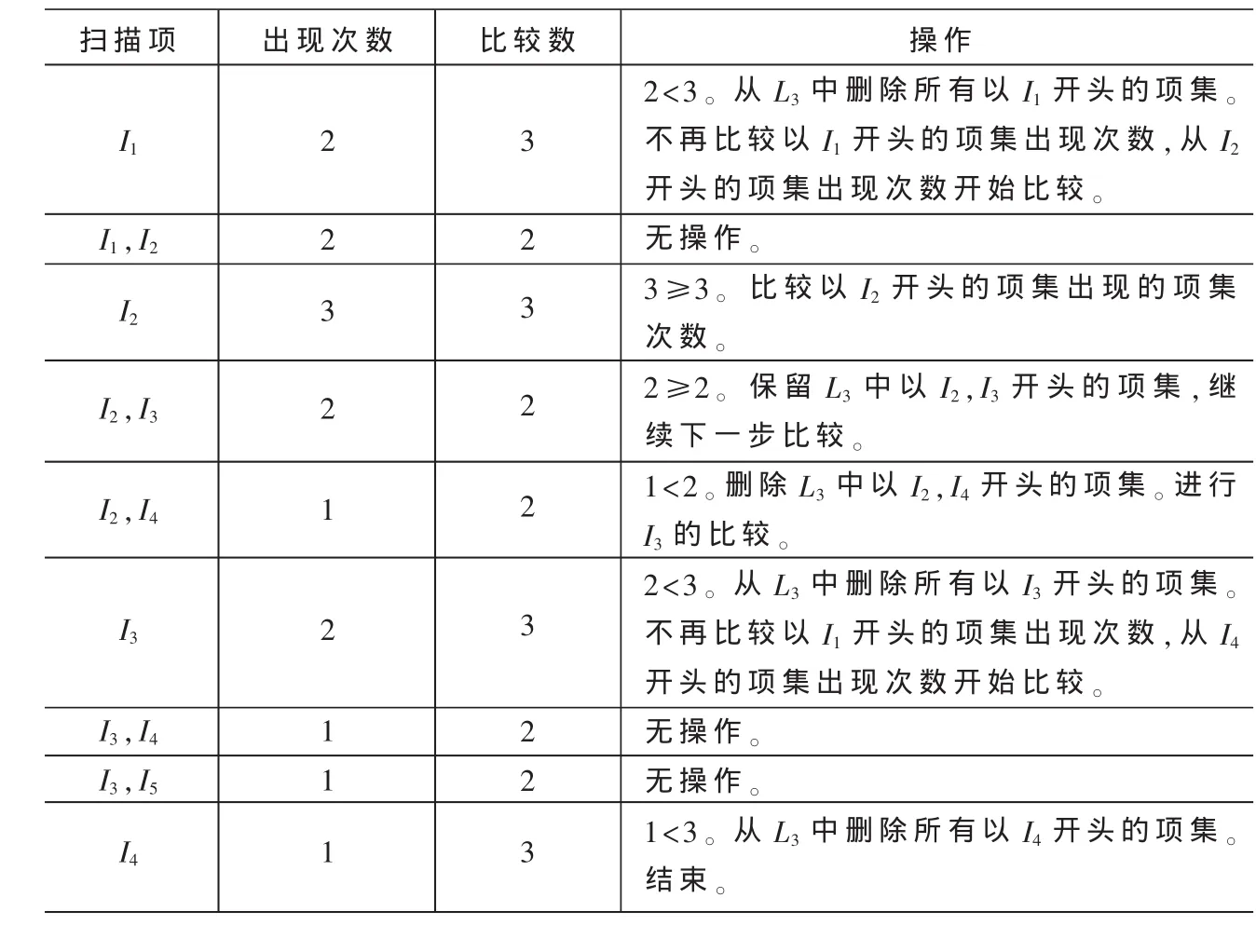
表1 删减L3中的项集
