基于AIC准则的气动位置控制系统辨识
2021-09-16徐志鹏
权 宁,徐志鹏
(1.徐州工业职业技术学院 机电工程学院,江苏 徐州 221000;2.江苏建筑职业技术学院 交通工程学院,江苏 徐州 221000)
引言
气动位置控制在自动化、工业机器人、装备制造等领域有着广泛的应用,通常以压缩空气作为动力源,与液压控制系统相比,其具有结构简单、安装方便、清洁无污染等便利[1-3]。随着制造水平的提升和计算机技术的发展,控制元器件的体积进一步减少、精度进一步提高,气动控制技术正朝着模块化、集成化、微型化以及智能化方向发展[4-6]。在实际工作过程中,气缸输出速度易受到负载的波动而变化、摩擦力造成黏滑振荡、气体流过阀口的复杂性等原因,导致气动系统是一个非线性控制系统,控制精度有待进一步提高[7-8]。通过对系统进行数学建模和仿真实验的方式研究气动位置控制系统的输入和输出特性,对提高系统模型的精度、定位的准确性具有一定意义。
1 组成与原理
1.1 系统组成
气动位置控制系统组成包括气缸、位移传感器、三位五通比例阀、数据采集卡、以及PC等[9-11],其中气缸型号为NCI-32-150-P-A;电位式位移传感器的型号MLO-POT-450-TLF;三位五通比例阀的型号MPYE-5-1/8HF-010-B。
1.2 工作原理
气动位置控制系统工作原理如图1所示,通过控制比例阀的开合度来控制A,B两腔的气流量,从而控制活塞或负载的位置,通过电位式位移传感器反馈的信息达到闭环控制。压缩空气经三位五通比例阀流经A或B腔,使A,B两腔出现压力差,在压力差作用下带动活塞运动。电位式位移传感器采集的信号经A/D转化后传送给PC,PC运算后经D/A转换后输出至比例阀。

图1 工作原理图
当系统输入参考电压时,通过电位式位移传感器检测活塞的实时位置,并将结果转化成电压信号反馈给控制器,实现气动位置控制系统的闭环控制。气动位置控制系统结构框图如图2所示,其中yd是系统参考信号;y是活塞实际位置信号;e是系统跟踪误差;u是PC控制信号。

图2 系统结构框图
2 系统模型
为便于对系统进行数学建模,假设系统介质为理想气体、无泄漏;系统无惯性与弹性负载,有黏性负载[12-15]。在气动位置控制系统中,压缩空气通过三位五通比例阀的流量与阀口结构、阀口开合程度以及上下游压强比有关。
气缸A,B两腔的压力变化方程:
(1)
式中,k—— 定压比热和定容比热之比
R —— 气体常数
Ts—— 环境温度
pa—— 气缸A腔压力
pb—— 气缸B腔压力
qma—— 气缸A腔气体质量流量
qmb—— 气缸B腔气体质量流量
A—— 气缸有效横截面积
L0—— 活塞初始位置
y—— 活塞位移
假设阀口的进口压力为ps保持稳定,出口压力为p,那么经过阀口的质量流量方程如下所示:
(2)
式中,λ—— 修正指数,一般取λ=0.25
Cf—— 临界压力比
ps—— 比例阀的进口压力
p—— 比例阀的出口压力
A(u) —— 比例阀开口面积
对于气动位置控制系统中气缸的A,B两腔,因为气体通过三位五通比例阀的质量流量qm是控制量u和阀口上下游压强pa与pb的函数,其中控制信号为二次函数A(u)=k1u2+k2u,所以气缸A,B两腔的质量流量qm有如下公式:
根据牛顿第二定律,可得气动位置控制系统的动力学方程:
(4)
式中,m—— 活塞与负载的总质量

Ff—— 摩擦力
由式(4)可知,摩擦力Ff是与速度有关的非线性函数:
(5)
式中,ba—— A腔黏性摩擦系数
bb—— B腔黏性摩擦系数
Fa—— A腔库伦摩擦力
Fb—— B腔库伦摩擦力
由式(1)~式(5)得系统模型:
(6)
实际工作过程中,气动位置控制系统受到外界温度、湿度等环境干扰,气体各项参数是一个动态变化的,其是一个非线性系统。为便于对位置控制系统分析与研究,忽略运动过程中的摩擦力,对fa(u,pa)与fb(u,pb)局部线性化处理,可得:
(7)
式中,x1—— 活塞位移
x2—— 活塞速度
x3—— 活塞加速度
b—— 系统未知增益
a1,a2,a3—— 系统未知参数
3 系统辨识
3.1 参数辨识
气动位置控制系统测试通常包含白色噪声和有色噪声。在系统参数辨识过程中利用增广最小二乘法以实现扩充参数的向量和数据向量的维数,利用D(z-1)将噪声集提到待观测序列中,实现有色噪声到白色噪声的转换,从而实现对有色噪声参数的无偏估计。
增广最小二乘法中的噪声模型:
A(z-1)z(k)=B(z-1)u(k)+D(z-1)v(k)
(8)
式中,u(k) —— 系统输入变量

z(k) —— 系统输出变量
当v(k)未知时,则采用增广最小二乘的递推算法:
(9)
3.2 阶次辨识
在气动位置控制系统中,系统的阶次是一个重要参数,但是在实际试验过程中一般无法提前获知。因此,需要在参数辨识之前要确定气动控制系统中的阶次,一般结构辨识方法主要有:F检验方法、FPE准则法、AIC准则法。
F检验法一般用于检验两个模型的差异性;FPE准则法一般利用模型进一步预报误差的方差来判定模型的阶数是否适用,误差的方差越小,则模型拟合度越好;AIC准则法既考虑了拟合模型对原始数据的接近程度,也考虑了模型中所含待定参数的个数,该准则不仅可以权衡所估计模型的复杂度,也可以衡量模型拟合数据的优良性。
通过上述3种结构辨识方法优劣比较,在气动位置控制系统辨识中,最优采用AIC准则,建立了白噪声和有色噪声2种模型。
(1)白噪声模型:
(10)
根据极大似然估计可得:
(11)
参数θn和噪声v(k)方差的极大似然估计值:
(12)


L—— 数据长度
(2) 有色噪声模型:
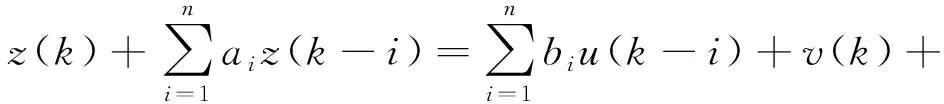
(13)
根据AIC准则原理知准则函数:
(14)

联立上式(10)~式(14),找到使得AIC(n,m)最小的n,m,即为气动位置控制系统模型阶次的估计值。
4 模型检验
为验证得到的系统辨识估计模型的可靠性,可通过验证该模型与系统过程输出残差序列{ε(k)}的白噪声。如果残差序列{ε(k)}可以视作零均值的白噪声序列,则认为模型是可靠的。
根据气动位置控制系统输入输出数据{u(k),z(k)}在系统模型中:
z(k)=G(z-1)u(k)+N(z-1)v(k)
(15)
式(17)中G(z-1)和N(z-1)是相应的传递函数估计量,则系统输出残差:
(16)
此时,模型的检验问题转换为“{ε(k)}是否白噪声序列”,检验方法如下:如果{ε(k)}是白噪声序列,则取样本ε(l)(l=1,2,3…),l为系统中的数据长度,假设ρε(l)为ε(k)的相关系数,则:
ρε(l)=Rε(l)/Rε(0)
(17)
式中,Rε(0)与Rε(l)是ε(k)的自相关系数。
若在系统数据长度有限,则ρε(l)的估计值表示成:
(18)
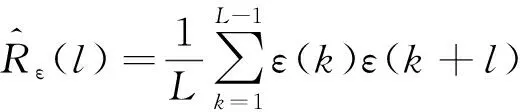

因此,系统模型检验问题转化为检验统计量t是否为m的中心χ2正态分布。


(20)
(21)
如果满足式(20)、式(21)要求,则认为{ε(k)}是零均值的白噪声序列,相应的辨识模型是可靠的。
5 实验验证
5.1 零点校准
本实验所用三位五通比例阀的型号是MPYE-5-1/8HF-010-B,其理论零点是5 V。由于系统长期使用或闲置影响比例阀控制精度,所以在实验前需要对比例阀零点校准。在零点调试过程中,给该系统一个周期为0.8 s,幅值为500 A的正弦信号作为零点的输入信号。当输出信号与输入信号变化趋势基本一致时,即为该系统的零点。如图3所示,实线是活塞的位置信号,虚线为系统零点经过调整设定为2058 μV。

图3 比例阀零点调试
5.2 数据采集
气动位置控制系统实验采样时间设定为10 ms,辨识过程设定数据长度为1000,实验设定逆M序列为7级。当幅值为1000 A时,数据采集曲线如图4a所示;幅值为1200 A时,其曲线如图4b所示。
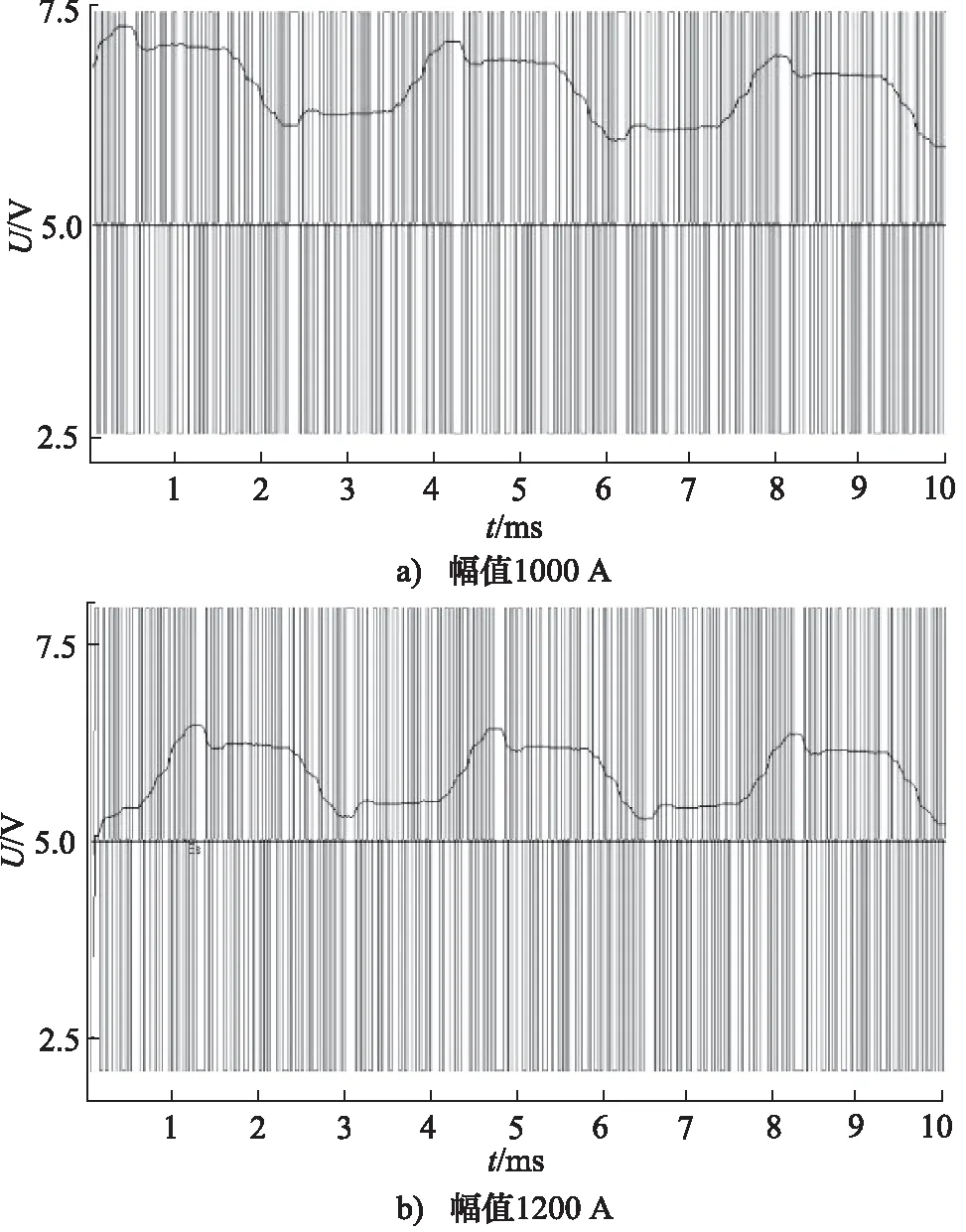
图4 数据采集曲线
5.3 结果分析
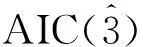

表1 幅值为1000 A时白噪声模型阶次
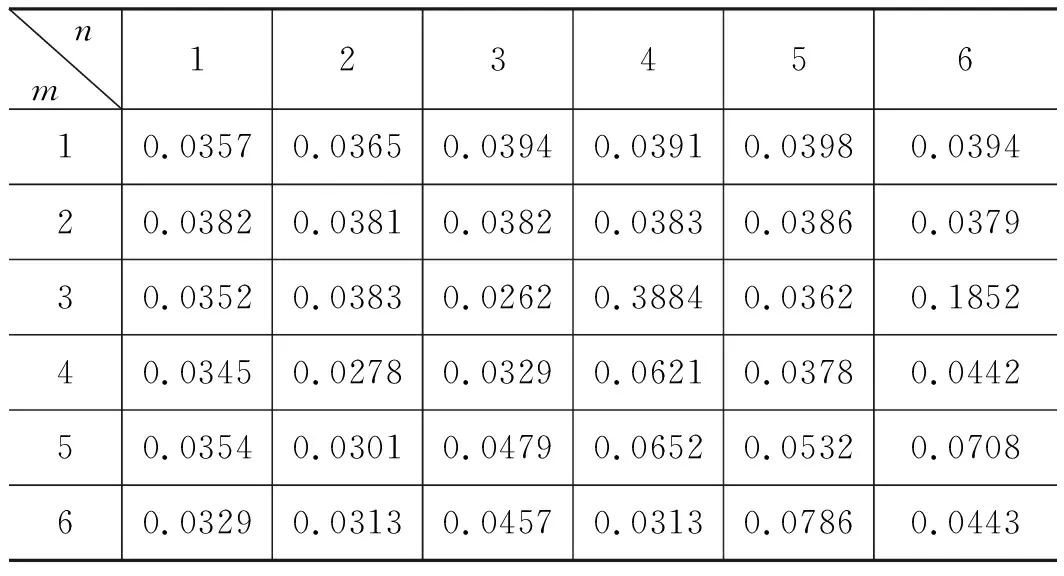
表2 幅值为1000 A时有色噪声模型阶次
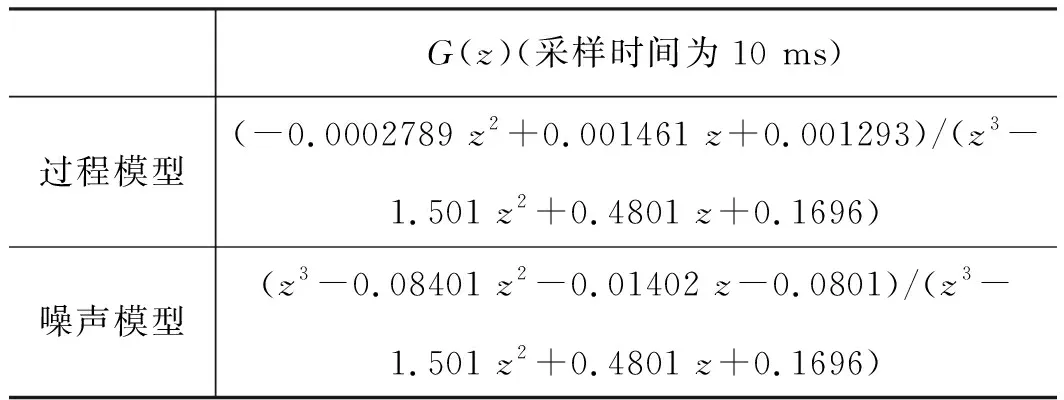
表3 幅值为1000 A时模型参数辨识

图5 残差图

表4 幅值为1000 A时自相关系数


表5 幅值1200 A时白噪声模型阶次
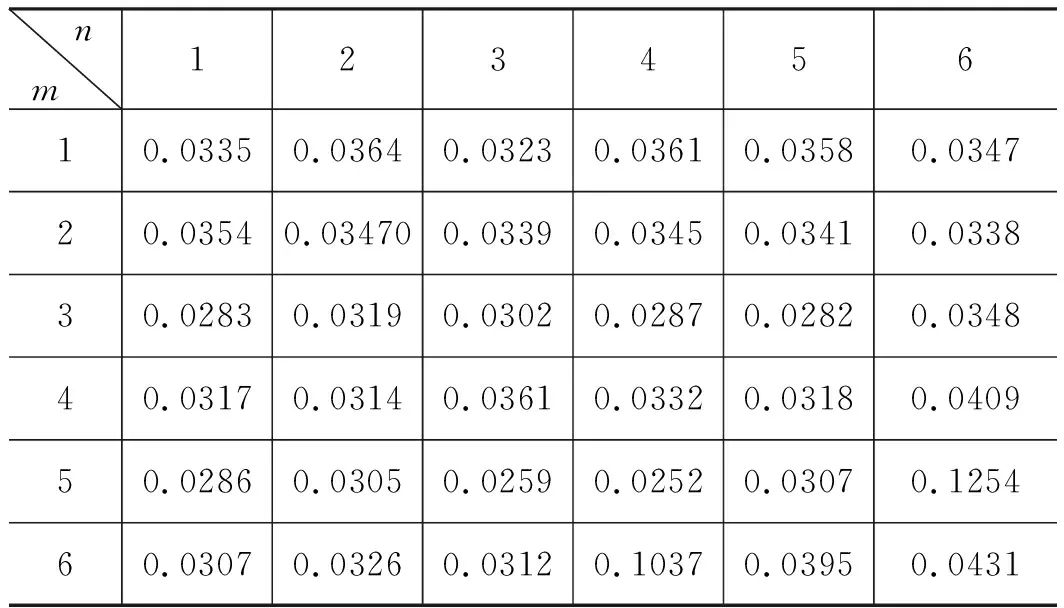
表6 幅值1200 A时有色噪声模型阶次

表7 幅值1200 A时模型参数辨识
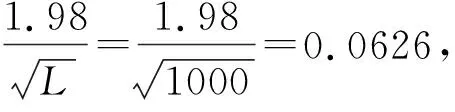

表8 幅值1200 A时自相关系数
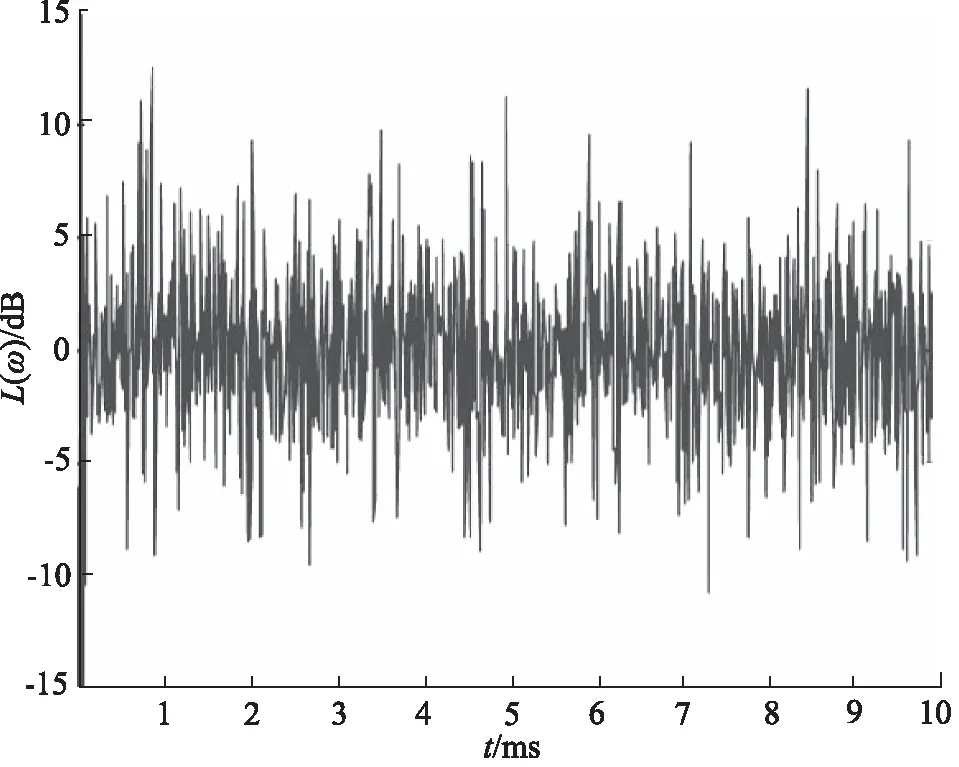
图6 残差图
通过图7可看知幅值分别为1000 A和1200 A时两种系统的传递函数基本上等价,说明在相同阶次的逆M序列且幅值在一定范围内,不同系统对模型参数的辨识影响较小。

图7 系统对比图
6 结论

