混合式步进电动机结构参数智能协同优化

裘信国，杨 昆，孟 彬，姜 伟

(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室，浙江 杭州 310014)

引言

混合式步进电动机作为小功率伺服控制系统中关键的伺服元件，凭借其体积小、性价比高、定位稳定可靠以及易于控制等优点在民用场合得到广泛应用[1]。近年来，随着混合式步进电动机应用到诸如液压设备、机器人和航空航天等领域，电机的性能要求不断提高，学者们为此提出了大量新型结构的混合式步进电动机[2-4]，设计高效的混合式步进电动机的结构优化方法具有重要的研究意义。

混合式步进电动机属于细齿结构的磁阻电机，由于其气隙很小，并且电磁场分布不均匀，使得电机的优化设计变得困难。因此，国内外学者对混合式步进电动机优化设计进行了如下的研究：STUEBIG等[5]针对混合式步进电动机提出了一种解析-数值相结合的电机分析方法；ERIC等[6]研究出一种混合式步进电动机的二维有限元与磁网络模型相结合的分析方法；SEKHARA等[7]利用MATLAB的PDE工具箱研究混合式步进电动机的本体结构参数对其转矩的影响；鲁炳林等[8]提出了一种相比于传统的齿层比磁导法[9]更为简单实用和计算精度高的齿层转矩计算转矩法；李鹏等[10]提出了一种通过模型等效变换的方法来获得混合式步进电动机的二维等效模型；侯胜伟[11]利用遗传算法对二相混合式步进电动机进行结构参数优化；方春仁等[12]基于ANSYS对混合式直线旋转步进电机进行了齿宽、齿高和气隙等齿层参数的优化。

大多数学者对混合式步进电动机进行分析计算时均采取在保证较高计算精度下简化电机的计算模型，对于混合式步进电动机结构优化方面的研究主要侧重于单一变量依次优化，而对于结构参数多变量优化方面的研究较少。但混合式步进电动机的结构参数之间是相互关联的，单变量参数优化的结果并非最优解，因此进行多参数优化分析更具有实践意义。因此本研究选用空心杯转子结构的轴向分相二相混合式步进电动机为研究目标，采用场路结合分析方法、三维有限元分析计算方法和智能协同优化方法相结合的方式，对电机的关键结构参数进行定量优化，并对优化结果进行有限元验证。

1 混合式步进电动机结构

混合式步进电动机主要由转子、定子、永磁体、线圈等组成，其结构如图1所示。转子由轴向充磁的永磁体及2段铁芯组成，转子铁芯开有45个小齿，2段铁芯无错齿。另外，为了减小转子转动惯量提高电机的动态响应能力，2段铁芯采用了空心杯结构。定子有4块铁芯，每块铁芯开有与转子相同的齿数，且4块铁芯之间存在错齿。定子1与定子2错开1/2个齿距角；定子3与定子4同样错开1/2个齿距角；定子2与定子3错开1/4个齿距角。定子1与定子2、定子3与定子4分别形成一个线圈槽口，线圈采用周向绕制。由于电机使用轴向分相的结构，不仅定子绕组的绕制变得更为简单，而且槽满率也得到了提高。

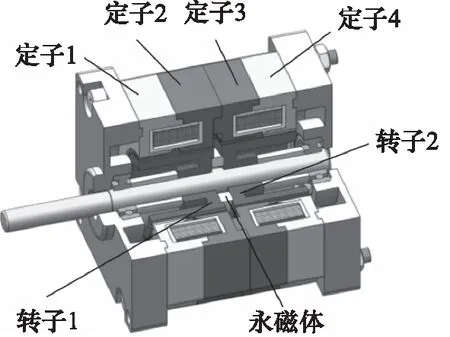
图1 混合式步进电机结构示意图

2 数学建模仿真

2.1 磁路分析

为得到电机的静态转矩解析方程，分析电机结构和运行参数对静态转矩的影响，利用等效磁路法[13-14]进行计算分析。假设铁磁材料在线性工作区，定转子铁芯磁导率为无穷大，忽略磁路漏磁带来的影响。基于以上假设可得到如图2所示的等效磁路。

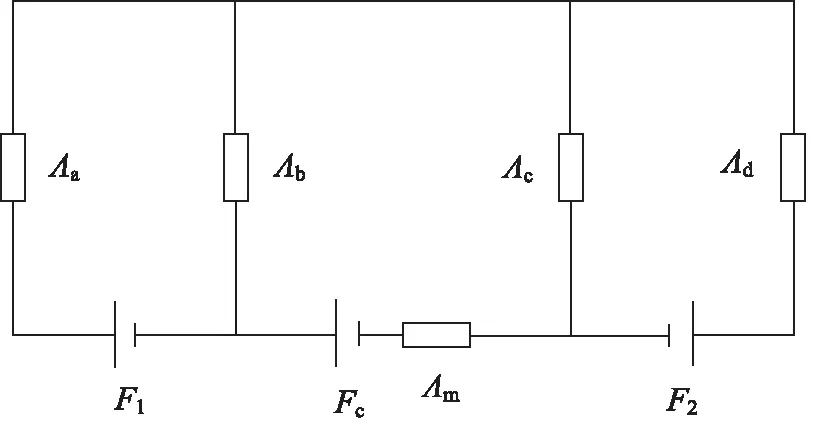
图2 混合式步进电动机等效磁路

图中,F1为第1线圈磁势；F2为第2线圈磁势；Fc为永磁体磁势；Λm为永磁体磁导；Λi为气隙a～d下的磁导；i为a～d。

为简化运算，通过磁路的线性叠加原理，将图2拆分为图3中3个磁路图。图中,U11，U12为气隙a和b下由第1线圈单独励磁产生的气隙磁压降；U23，U24为气隙c和d下由第2线圈单独励磁产生的气隙磁压降；Upm j为气隙i下由永磁体单独励磁产生的气隙磁压降，j为1～4。

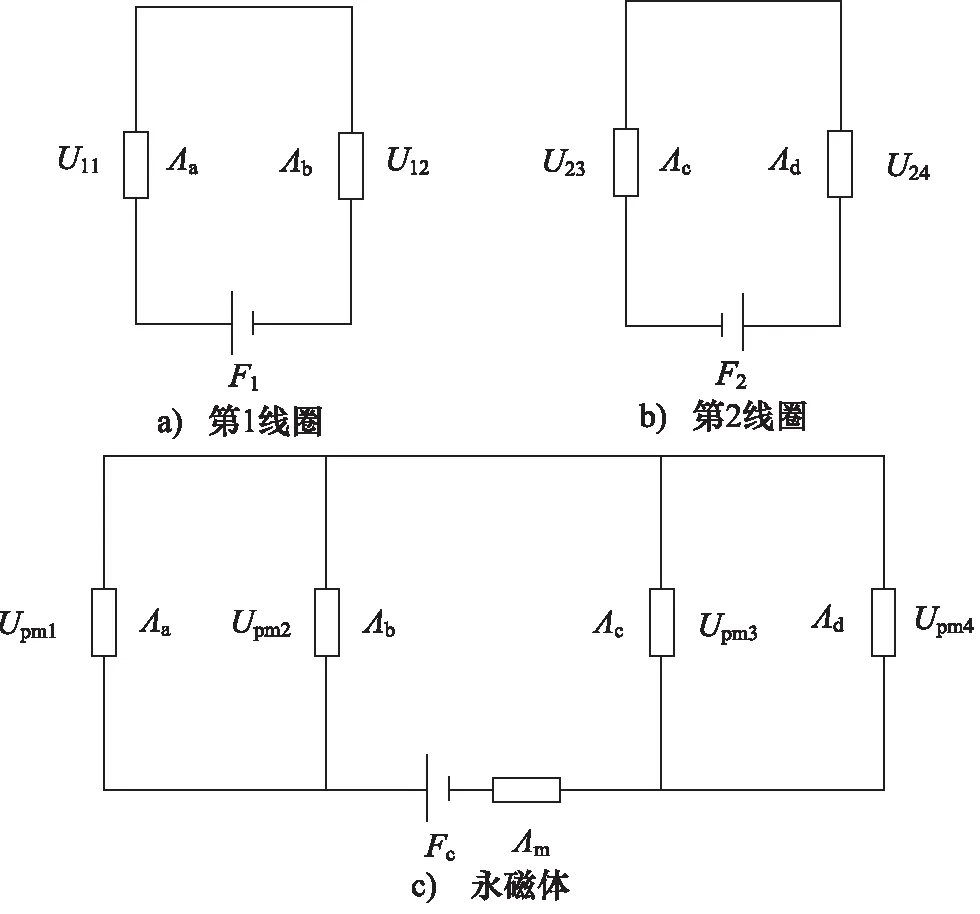
图3 等效磁路图的线性分解

忽略主磁导中高次谐波分量的影响，则转子和定子各个齿下的气隙磁导Λ为:

(1)

式中,Λ0—— 1个齿下的平均气隙磁导

Λ1—— 1个齿下的气隙磁导基波幅值

θe—— 定子与转子的齿中心线夹角的电弧度

电磁静转矩可以通过气隙总磁共能对转子转角偏导求得。在线性叠加条件下，电机的气隙总磁共能为：

(2)

式中，Ui—— 气隙i下的磁压降，i为a～d

W′ —— 电机的气隙总磁共能

电机的静态转矩为：

(3)

式中,Zr—— 电机转子的齿数

如图3a所示，当第1线圈单独励磁时，a和b气隙下的磁压降为：

(4)

如图3b所示，当第2线圈单独励磁时，c和d气隙下的磁压降为：

(5)

如图3c所示，永磁体的左右两侧磁路对称，因此永磁体单独励磁各个气隙产生的磁压降为：

(6)

各个气隙下的电磁静态转矩表示为：

(7)

将式(1)～式(6)代入式(7)后化简得:

(8)

其中:

(9)

当两线圈励磁满足F2=F1的情况时，电机的静态转矩公式可进一步简化为:

(10)

其中:

(11)

式中，λ为失调角。

由式(10)、式(11)可知，最大静态转矩Tm和转子齿数Zr、气隙磁导基波幅值Λ1、绕组电流、线圈匝数、永磁体工作磁势等结构和运行参数相关。在气隙a下定转子齿相互错开π/4电弧度时，电机输出静态转矩最大。

2.2 有限元模拟

为了进一步探究电机结构参数与运行参数对电机静态转矩的影响，以定转子的气隙g、齿宽比bt/t、齿高ht、转子杯壁厚hr为变量，以电机静态转矩T为目标，对混合式步进电动机进行三维静磁场的仿真[15]，分析矩角特性曲线的变化。仿真中，导磁材料为DW310-35的硅钢，磁钢材料为NdFe35的钕铁硼，仿真求解器迭代步数为10，精度误差为4。

由图4a所示，随着定转子气隙的减小，电机的转矩值明显提升；由图4b所示，随着齿宽比的减小，电机的转矩值呈现增大的趋势，当齿宽比取为0.3时，矩角特性曲线的波形发生畸变；由图4c所示，随着齿高的增大，电机的转矩值变化趋势不明显；由图4d所示，随着电机转子杯壁的厚度增大，电机的转矩值明显提升。

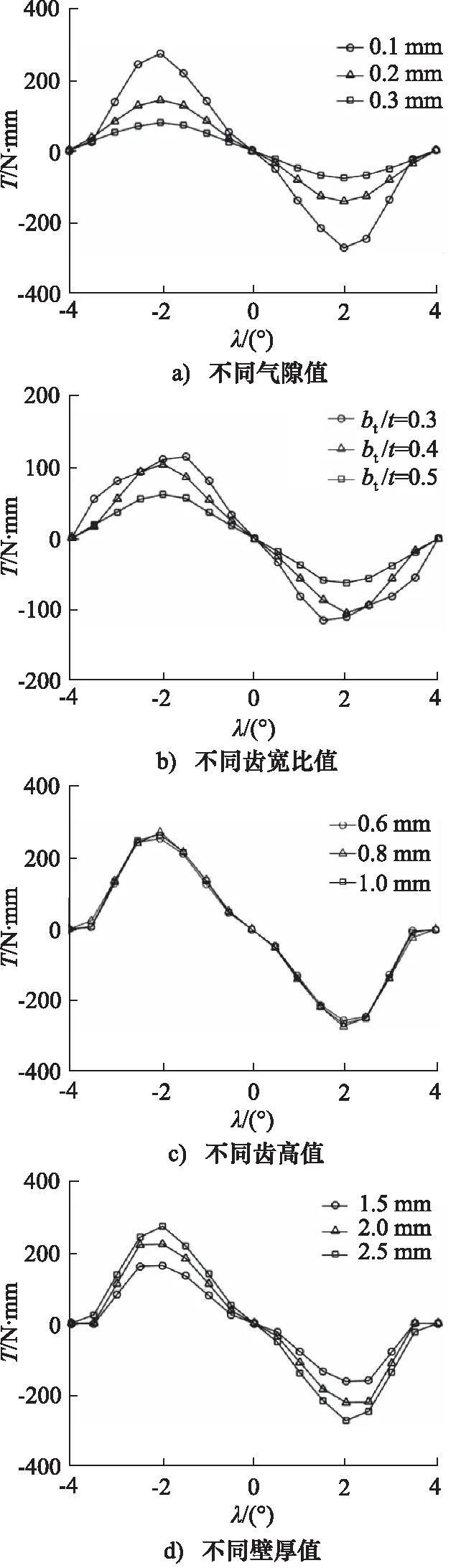
图4 有限元模拟的矩角特性曲线

3 智能协同优化设计

由于有限元模拟采用单一变量分析，而电机的结构参数之间是有关联性的，关联参数的取值不同将对结果产生较大影响。为了得到定转子的气隙g、齿宽比bt/t、齿高ht、转子杯壁厚hr的最优匹配值，有必要对结构参数进行多变量全局搜索。因此本研究提出一种基于正交试验、BP神经网络和遗传算法的高效精准的协同优化方案[16-18]，计算出电机结构参数区间内的最优设计参数，并预测出电机最大静态转矩值。

3.1 BP神经网络初始数据库

由于BP神经网络可调参数较多，参数的不同会对网络产生明显影响，为了更好地评判网络对于参数与目标之间的拟合程度以及网络的泛化能力，因此使用正交试验选出均衡性和具有代表性的数据作为BP神经网络的测验数据。以电机的气隙、齿宽比、齿高、杯状转子壁厚为优化变量，以电机的最大静转矩为优化目标，优化变量约束条件设计为：

(12)

在约束条件内，采用四因素三水平的全面试验方案，选取81组数据作为BP神经网络的训练数据，如表1所示；采用四因素三水平的正交试验方案L9(34)，选取9组数据作为BP神经网络的测验数据，如表2所示。

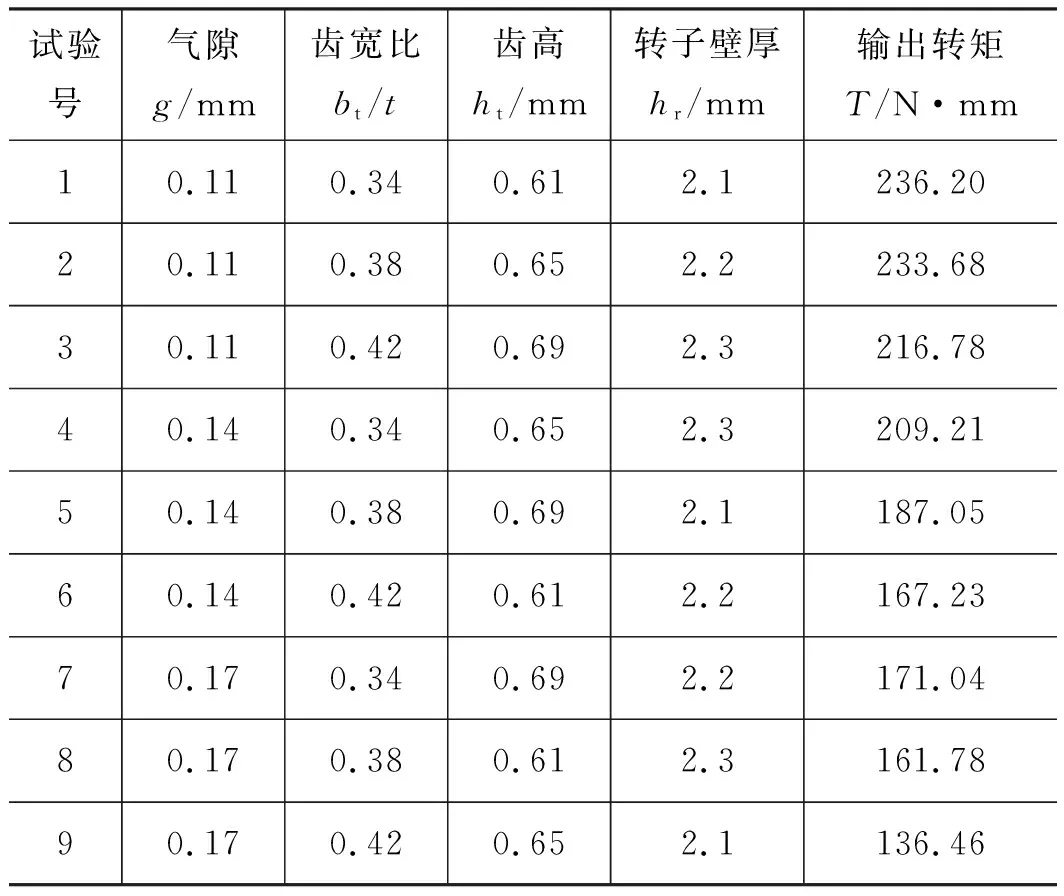
表1 BP神经网络预测数据

表2 优化参数因素-水平表

3.2 BP神经网络模型

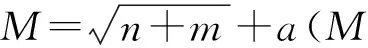
net.b{1}=[-3.6-1.42.34.6-0.41.24]T

net.b{2}=-3.2

net.lw{2,1}=[1.2-3.51.60.60.52.9-0.8]

(13)

3.3 遗传算法

遗传算法是一种拟自然界遗传机制和生物进化论而成的并行随机搜索最优化方法。遗传算法具有高效启发式搜索、并行计算等特点，以训练好的BP神经网络计算电机的最大静态转矩作为种群的个体适应度，通过个体的选择、交叉以及变异实现全局范围内寻优，找到最优解以及对应的变量参数。利用MATLAB进行遗传算法编程，程序中的主要参数如表3所示。

表3 遗传算法主要参数

3.4 智能协同优化结果分析

BP神经网络的拟合度如图5所示，输出T,目标Y，预测值与有限元仿真值之间的拟合度高达99.8%，达到了理想的拟合效果。对正交试验选取9组测验组进行BP神经网络预测，结果如表4所示，BP神经网络预测的所有数据的相对误差均在5%内，满足精度要求，可以认为此网络具有良好的预测性能。

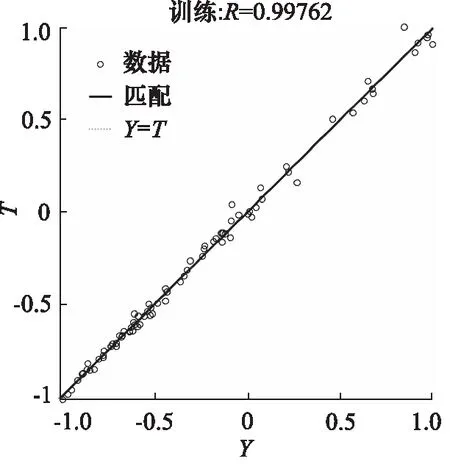
图5 样本数据匹配结果

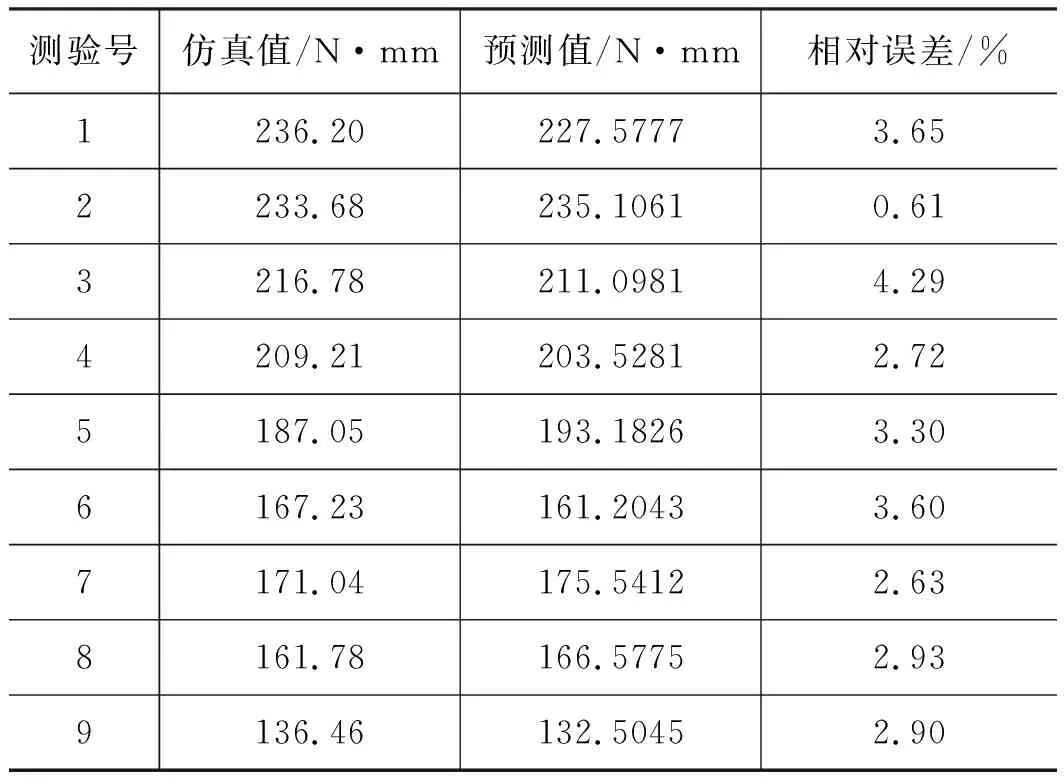
表4 网络预测值与仿真值对比

以BP神经网络计算个体适应度，在参数约束区间内使用遗传算法进行并行搜索，寻找出参数的最优解。遗传算法的电机静态转矩进化寻优过程如图6所示。随着遗传代数n的增加，适应度值趋于稳定，最终寻得最优参数为：g=0.1 mm，bt/t=0.37，ht=0.84 mm，hr=2.5 mm；最优目标值Tm=279.4657 N·mm。

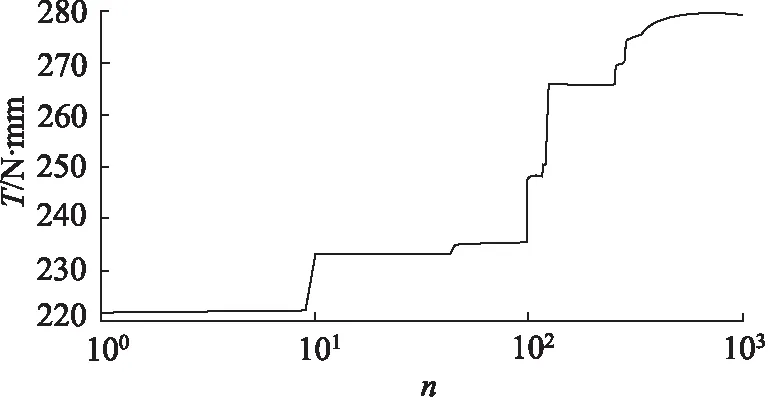
图6 最大静态转矩适应度曲线

根据遗传算法搜索出的最优参数，对电机的三维模型进行重新绘制并进行ANSYS Maxwell-3D有限元仿真，在两线圈通入1.5 A直流电时，仿真的矩角特性曲线如图7所示，其中最大静转矩值为293.55 N·mm，最优目标值与仿真值的相对误差为4.8%，可以认为智能协同优化结果具有很高的可信度。

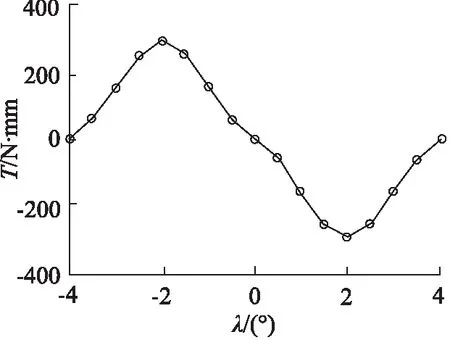
图7 优化后的有限元模拟的矩角特性曲线

4 试验

为验证前述电机优化的准确性，根据结构优化参数制作了试验样机并搭建如图8所示的矩角特性测试系统。

图8 矩角特性测试系统

电机、静态扭矩传感器以及固定块通过联轴器依次相连，此时，电机的转轴无法旋转。电机通过联轴器与静态扭矩传感器相连，其中静态扭矩传感器的型号DRFL-I-5-n-K(扭矩量程为5 N·m，扭矩示值误差为±0.1%)，静态扭矩传感器的另外一端通过联轴器与固定块相连，使得电机转轴无法旋转。在上述情况下，电机的控制器给予A相与B相的线圈期相位差为90°的正弦波电流，使得电机内部磁场发生了360°的旋转，此时控制器的电信号电流值与静态扭矩传感器测得的电压值通过单片机同步读取到计算机。由于控制器的电流值对应电机的磁场旋转电角度，因此，控制器的电流值可以换算为电机的失调角。而扭矩传感器的电压值可以换算为电机的静态转矩值，从而通过以上换算得到的失调角以及与其相对应的静态转矩这2组数据，可以绘出电机在1个齿距角下的矩角特性曲线，试验曲线如图9所示，采样点数为n1。

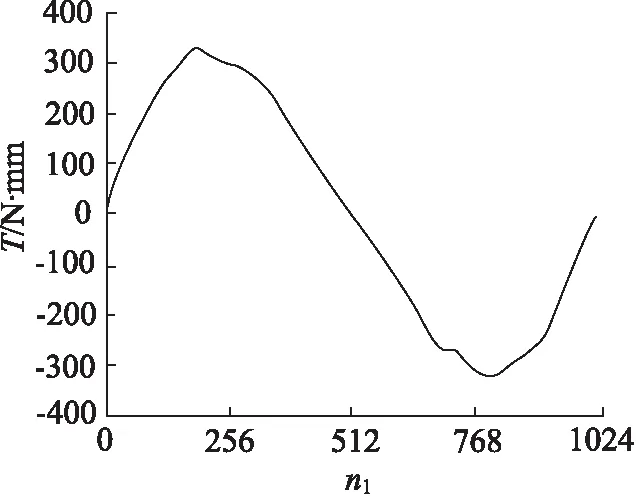
图9 矩角特性曲线

根据测试结果可知，电机的试验静态最大转矩为256 N·mm，而优化预测的静态最大转矩为279 N·mm，试验所得结果与优化预测结果的相对误差值为8.98%。相比有限元仿真结果294 N·mm，试验结果略微偏低，考虑试验误差的可能原因为：软磁材料加工易变形、定转子齿齿形加工精度限制、电机装配误差以及试验过程误差等。

5 结论

(1) 采用智能协同优化方法对轴向分相式电机进行了结构参数优化，得到了电机结构参数的最优尺寸为：g=0.1 mm，bt/t=0.37，ht=0.84 mm，hr=2.5 mm;

(2) 由BP神经网络预测的电机最大静态力矩值相比于有限元仿真值的相对误差均在5%内，最终优化的结构参数相对应的BP神经网络预测最大静转矩值为279.4657 N·mm，相对应的有限元仿真值为293.55 N·mm，相对误差为4.8%;

(3) 在ANSYS Maxwell-3D有限元模拟仿真求解器迭代步数为10，精度误差为4的前提下，服务器运算时间为2 h；而智能协同优化方法中的BP神经网络一旦电机模型拟合成功，在遗传算法种群规模为20，最大代数为1000的前提下，最大静转矩的笔记本运算时间为1～2 min。